飞推一体化飞行器多模态计力体系及升阻性能研究

李恒，钟易成，史永运

(1. 南京航空航天大学 江苏省航空动力系统重点实验室，江苏 南京 210016；2. 南京普国科技有限公司，江苏 南京 210016)

0 引言

涡轮基组合循环发动机(TBCC)由于其宽广的飞行包线以及良好的比冲性能等优势，更适合作高超声速飞行器的动力方案[1-2]。同时，飞行器机体与推进系统一体化设计也成为高超声速飞行器发展中不可或缺的一项关键技术[3]。飞推一体化布局形式导致飞行器机体和发动机形成的流场存在强烈的耦合影响[4-5]，同时又因为推进系统在不同模态下都对应着不同的推进系统结构，进而不能准确计算并评估飞行器气动性能。因此，有必要针对飞推一体化高超声速飞行器多模态工作状态下进行计力方法研究。

目前国外学者针对高超声速一体化飞行器计力方法进行了深入研究[6-9]，国内国防科大[10-11]及西北工大[12]等高校学者在继承了国外计力方法理论基础上，对不同气动外形布局的一体化飞行器进行了数值仿真分析，李蔚霆等[13]开展了高超声速进气道三维构型设计和前体构型设计，进行前体对进气道的气动性能影响研究，但并未针对推进系统处于双通道模式下飞行器的计力体系及升阻性能进行有关研究。本文主要研究双通道模式飞行器气动/推进力计算方法，通过数值仿真技术对TBCC一体化飞行器在不同工作模态下进行升阻性能研究与部件受力分析。

1 飞行器运动分析

1.1 飞行器受力分析

为了分析飞行器的气动性能与推进性能，必然要解决飞行器飞行过程的受力分析问题，故需建立一套完备的飞行运动分析体系[14]，保证运动分析体系中各项力不漏力，也不重复计力，为便于后续将各项力根据计力体系方法分别划分到飞机气动型面和推进系统型面打下可靠基础。

为了便于对一体化构型飞行器的飞行性能进行分析，首先定义气流坐标系和机体轴向坐标系，同时为了对比力学体系划分方案，仅考虑垂直平面内无侧滑飞行时作用在飞行器上的力，如图1所示。

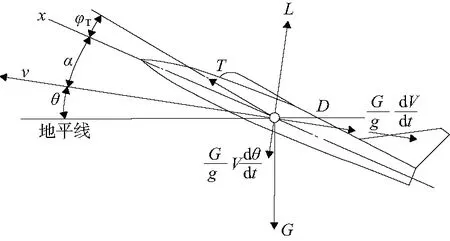
图1 垂直平面内无侧滑飞行作用在飞机上的力

1.2 动力学方程

在气流坐标系下，飞行器飞行动力学方程普遍写为如下方程组[15]：

mdV/dt=Tcos(α+φT)-D-Gsinθ

(1)

mVdθ/dt=Tsin(α+φT)+L-Gcosθ

(2)

式中：α为迎角；V为飞行速度；T为推力或拉力；G为重力；θ为航迹倾斜角；φT为推力或拉力作用线与飞机迎角基准线之间的夹角。

2 计力体系建立

计力体系的确定包括两项内容：划分气动/推进界面(API)和发动机/机体界面(EAI)，确定气动力/力矩和推进力/力矩的计算方法。

2.1 API/EAI划分方法研究

1)API划分方法研究

气动型面与推进型面的界面划分称为API，作用是划分气动学科与推进学科的主要负责型面，如图2所示(本刊黑白印刷，相关疑问咨询作者)。

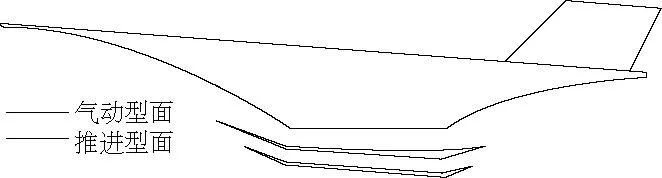
图2 API划分示意图

NUMBERS K[8]在其发表的高超声速推进系统计力体系中详细给出了各种API划分方法及优缺点，如表1所示。

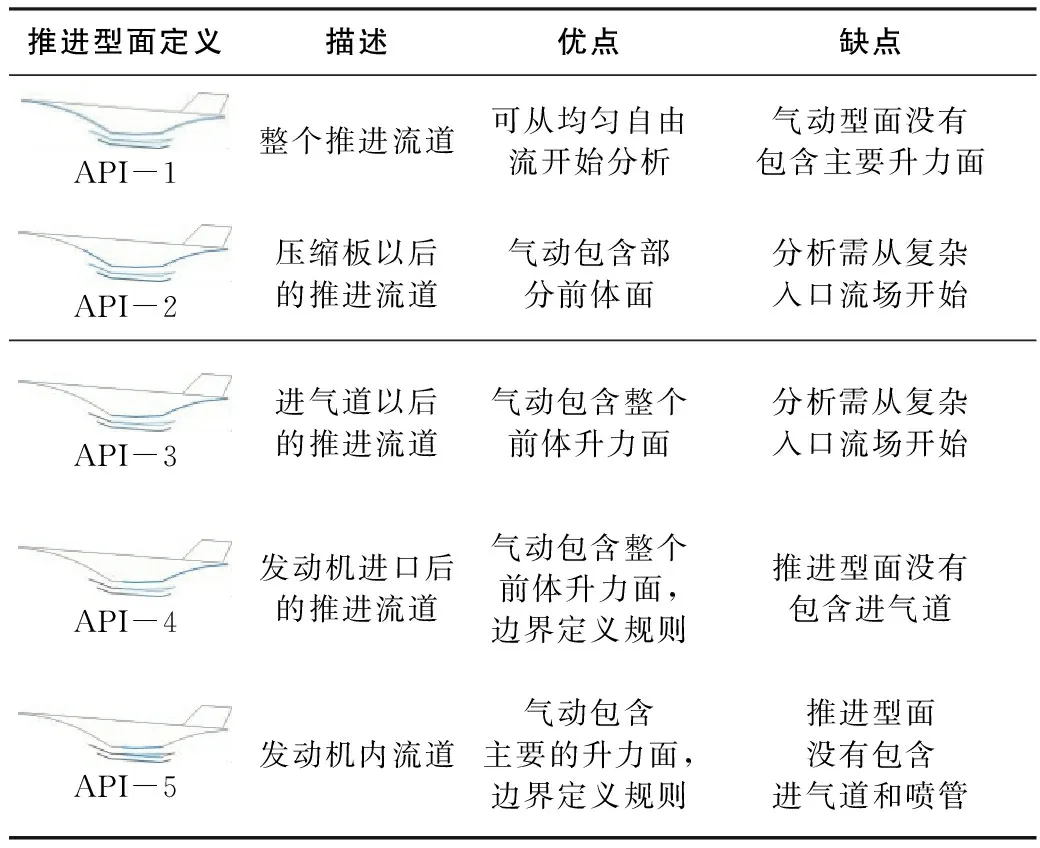
表1 API划分方法介绍及优缺点

2)机体/发动机界面(EAI)划分

发动机型面与机身型面的界面划分称为EAI。如图3所示，根据EAI的划分，运用动量定理计算发动机进口面至喷管喉部之间流管产生的推力即为发动机产生的内推力。

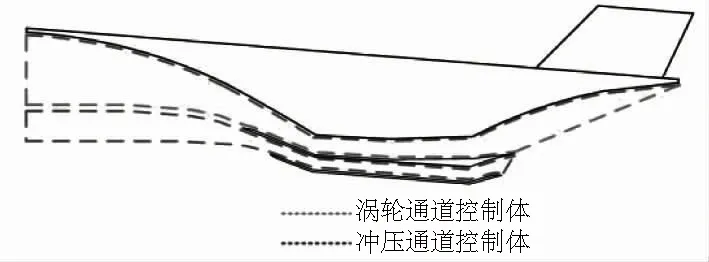
图3 EAI划分示意图

EAI划分确定了发动机内推力的计算边界，各种EAI划分方法以及各自的优缺点对比如表2所示。

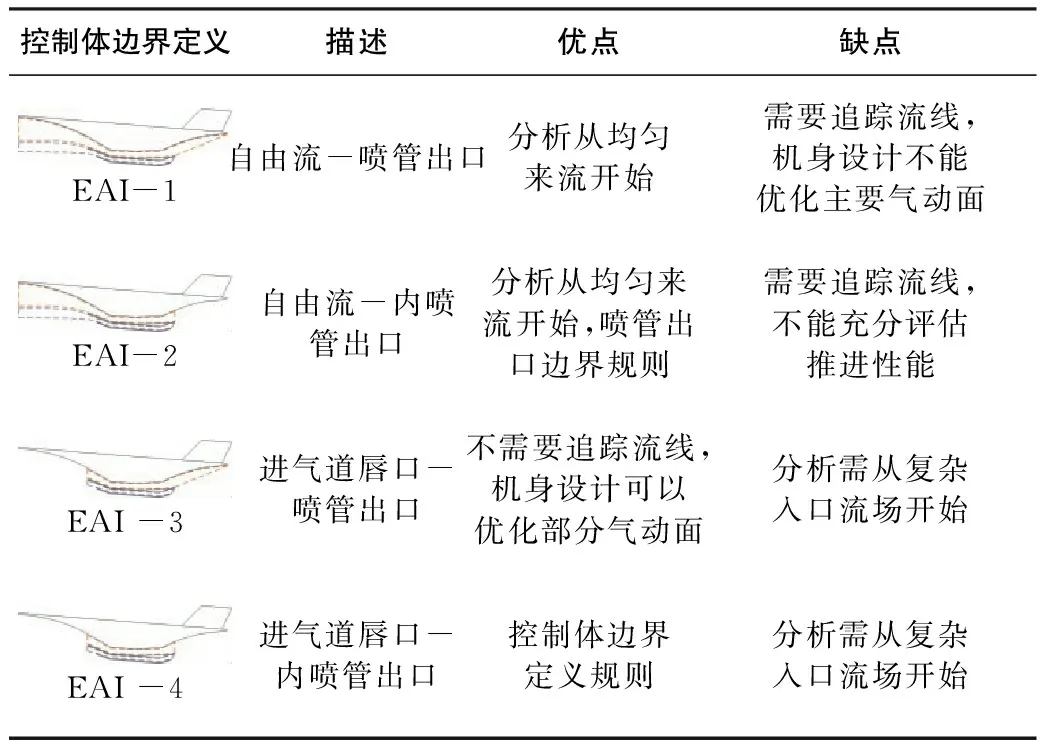
表2 EAI划分方法介绍及优缺点

2.2 气动/推进力计算方法研究

将飞行器所有型面根据API方案分别划归到气动与推进型面中去，通过计算型面上所受压力和摩擦力可得到型面所受合力，将各型面合力整合到气动与推进模块中可得到飞行器所受气动力与推进力，最后通过将机身轴向坐标力转换到气流坐标系力得到飞行器所受升阻力。

1)单通道模式气动/推进力计算方法

单通道模式下涡轮通道关闭，只有冲压发动机在工作，冲压模态飞行器二维简图如图4所示。由于一体化飞行器气动模块和推进模块耦合强烈，NUMBER K建议采用API-2以兼顾气动分析和推进分析两方面的需求，同时为了更方便准确获得控制体上下游计算面参数，选择EAI-1方案。

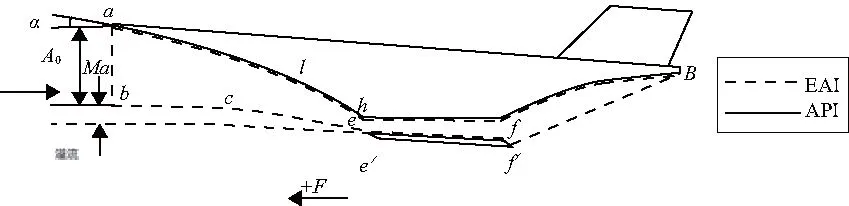
图4 推进系统单通道飞行器二维简图

通过对飞行器内外壁面所受压力以及摩擦力进行积分，可得到全机所受合力，即：

FT=Fint+Fext

(3)

Fint=Fint,p+Fint,f

(4)

Fext=Fext,p+Fext,f

(5)

合力在机身轴向分力记为FTX，机身法向分力记为FTY，对飞行器受力分析可得

FTX=T-Fa-Dadd

(6)

式中：T为推进系统推力；Fa为机身轴向气动力；Dadd为进气道溢流阻力。

由式(3)-式(6)可推导得出推力T的计算公式：

(7)

升力L与阻力D可由机身气动轴向分力Fa和机身法向分力FTY表示为：

L=FTYcosα-Fasinα

(8)

D=FTYsinα+Facosα

(9)

2)双通道模式气动/推进力计算方法

涡轮冲压过渡模态下涡轮与冲压通道都打开，涡轮和冲压发动机共同工作，过渡模态下飞行器二维简图如图5所示。

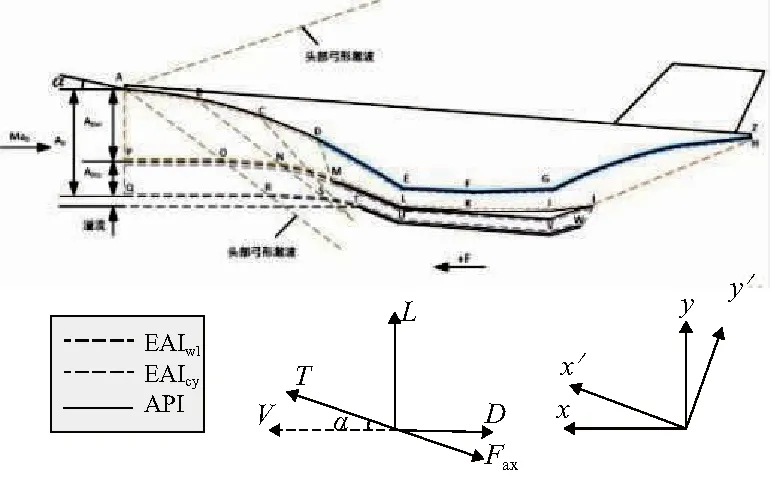
图5 推进系统双通道飞行器二维简图

飞行器过渡模态下气动与推进力计算公式推导方法与单通道气动与推进力计算公式推导方法同理。由于推进系统采用外并联式TBCC布局，故气动与推进力计算控制体分别由涡轮和冲压两个并联控制体组成。分别对两个控制体进行受力分析，计算得到涡轮和冲压通道受力，依据所选计力方案整合分类双通道所受所有的力，推导得到飞行器升阻力与推力计算公式。

对单通道飞行器推力受力公式(7)中每项力的定义和作用面，简化受力计算公式，针对不同的API/EAI划分方法选择各项力组合搭配，形成一个通用的计力体系推力计算方法库。

对推进系统推力计算公式中各项力进行定义：

式中：Tnozzle,wl-Tfree,wl表示涡轮流道控制体进出口冲量差；Tnozzle,cy-Tfree,cy表示涡轮流道控制体进出口冲量差，即控制体所受合外力；Ffore表示前体面所受压力与摩擦力对前体面积的积分之和，Dadd表示溢流气流对进入进气道流管的作用力积分。所有这些力作用位置都可由下标标明。

计力方案选择API-2与EAI-1组合计力方案，同理可推导得到：

Fa=Ffore+Fjs

(10)

Dadd=Dadd,wl+Dadd,cy

(11)

FTX=Fint,x+Fext,x=Ffore,x+Fjs,x+Finlet,x+Fnozzle,x+Ffore,x+Fengine,x

(12)

FTY=Fint,y+Fext,y=Ffore,y+Fjs,y+Finlet,y+Fnozzle,y+Ffore,y+Fengine,y

(13)

双通道模式下发动机推力T:

T=FTX+Fa+Dadd=Ffore,x+Fjs,x+Finlet,x+Fnozzle,x+Ffore,x+

Fengine,x+Ffore+Fjs+Dadd,wl+Dadd,cy

(14)

同理，可得到升力L与阻力D的计算公式与式(8)-式(9)一致。

3 一体化飞行器模型及数值仿真

3.1 二维TBCC一体化飞行器建模

1)进气道二维模型

当飞行马赫数≤3.0时，推进系统处于双通道模式，即涡轮和冲压通道同时打开。如图6所示，上方为冲压通道，下方为涡轮通道；当飞行马赫数>3.0时，涡轮通道关闭，冲压发动机单独工作，二维模型如图7所示。

图6 二元可调双通道进气道示意图

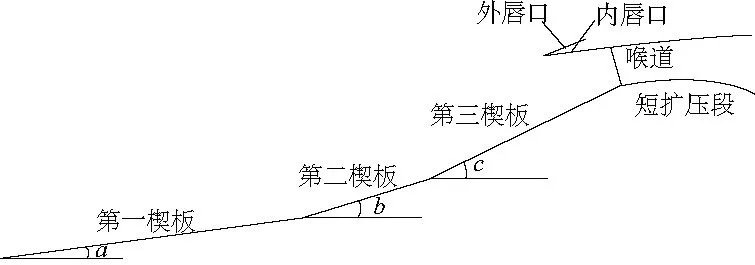
图7 二元可调单通道进气道示意图

2)喷管二维模型

双通道模态下的可调喷管方案二维模型示意图如图8所示，上方为涡轮通道，下方为冲压通道；单通道模式下，涡轮通道关闭，冲压喷管型面固定不变，如图8虚线所示。

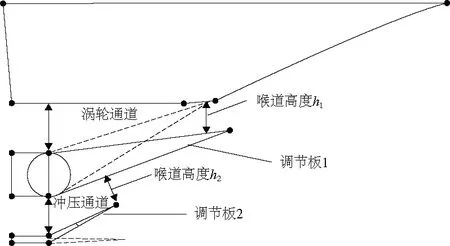
图8 二元可调双通道喷管示意图

3.2 网格划分及边界条件设置

1)网格模型介绍

采用结构网格进行数值仿真，如图9和图10所示。涡轮与冲压发动机同时打开时网格总数为176 606，只有冲压发动机工作时网格总数为123 054。

图9 双通道模态一体化飞行器网格模型图

图10 单通道模态一体化飞行器网格模型图

2)边界条件设置

一体化飞行器流场数值仿真采用有限体积法，控制方程采用N-S方程，流场模拟气体为理想气体，湍流模型为k-ωSST模型。

由飞行高度及飞行马赫数可获得大气环境参数和远场计算边界条件，具体参数如表3所示。

表3 飞行状态下大气参数

由于本文不对发动机内部燃烧反应进行性能仿真，不考虑发动机内复杂流场影响，所以直接在喷管进口处给定一个流场进口边界条件，具体参数如表4所示。

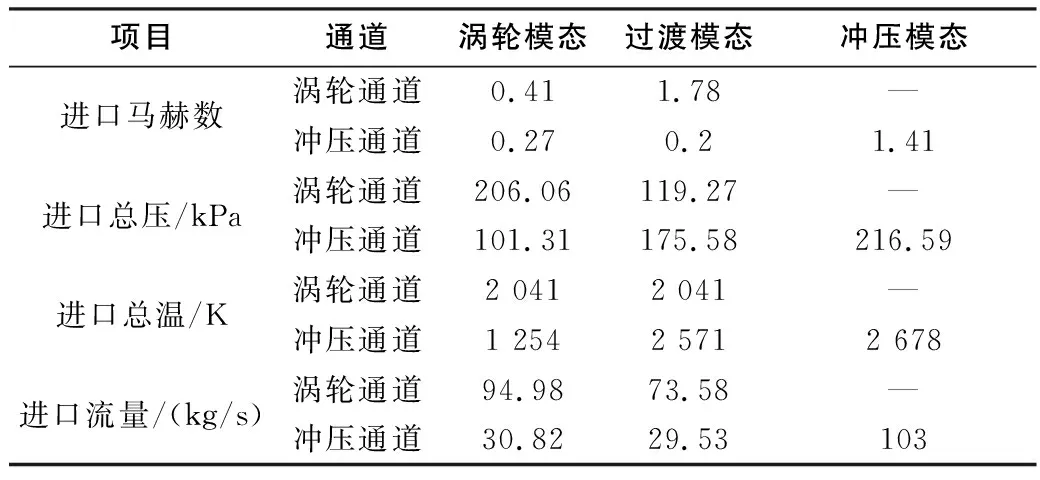
表4 喷管进口边界条件

4 升阻性能研究

4.1 升阻特性研究

通过CFD数值仿真，提取飞行器型面受力及控制体进出口截面气流参数可获得飞行器总升力L、总阻力D，进而计算飞行器升力系数CL,阻力系数CD以及升阻比L/D随飞行攻角的变化趋势，分析不同API划分对飞行器升阻特性的影响。其中：

(15)

(16)

式中：ρ∞表示远前方自由来流大气密度；v∞表示远前方自由来流速度；S表示机翼参考面积。由于本文研究的是二维构型，机翼参考面积由前体面加部分机身表面在二维模型中的长度×宽度得到，宽度取1m。

1)仿真计算结果

静压分布云图如图11-图13所示。

图11 Ma=1.2，4°攻角全机静压分布图

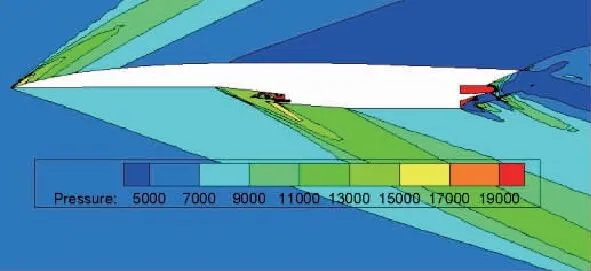
图12 Ma=3.0，4°攻角全机静压分布图

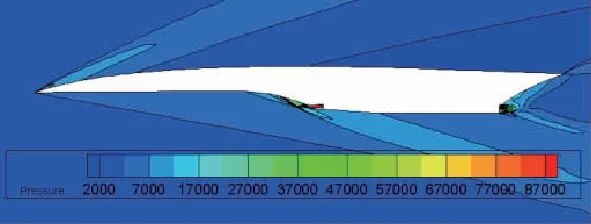
图13 Ma=5.0，4°攻角全机静压分布图

2)升阻性能曲线

由静压分布云图可看出，远前方来流在机头位置产生上下两道弓形压缩波使气流减速增压，气流经机身下表面斜激波不断增压，机身上表面气流经弓形压缩波短暂增压后在机身上表面后段膨胀加速。随着攻角的增加，飞行器下表面激波强度增强，上表面压缩激波强度减小，上下表面静压差增大，导致飞行器阻力系数、升力系数和升阻比均随攻角的增大而增大，如图14-图16所示。升力系数与攻角基本成线性关系，阻力系数与攻角大致成二次曲线关系，反映到升阻比上可看到变化趋势先升后降，涡轮模态在4°攻角时升阻比最大，其余两个模态在6°攻角时升阻比最大。同时由于Ma=1.2模态下机头产生了脱体激波，气流经脱体激波后迅速增压减速，飞行器上下表面静压差进一步增大，导致涡轮模态升力系数和阻力系数增大。

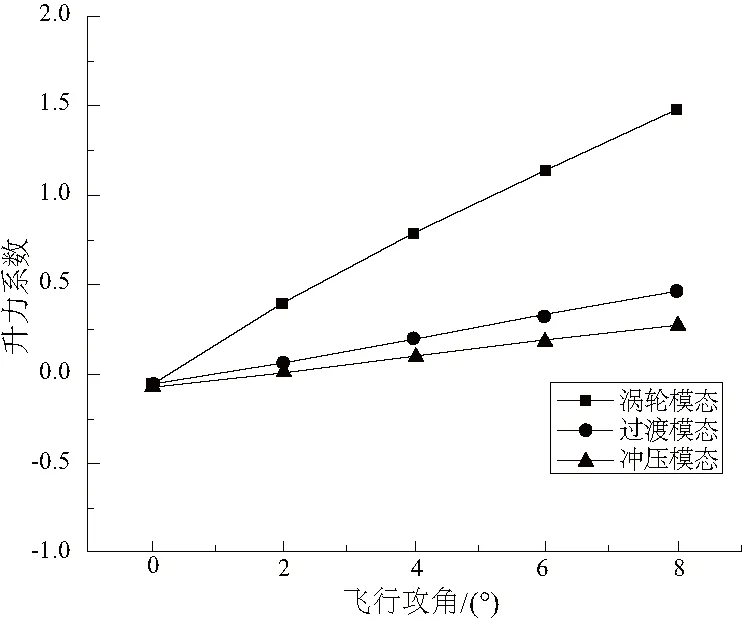
图14 升力系数曲线

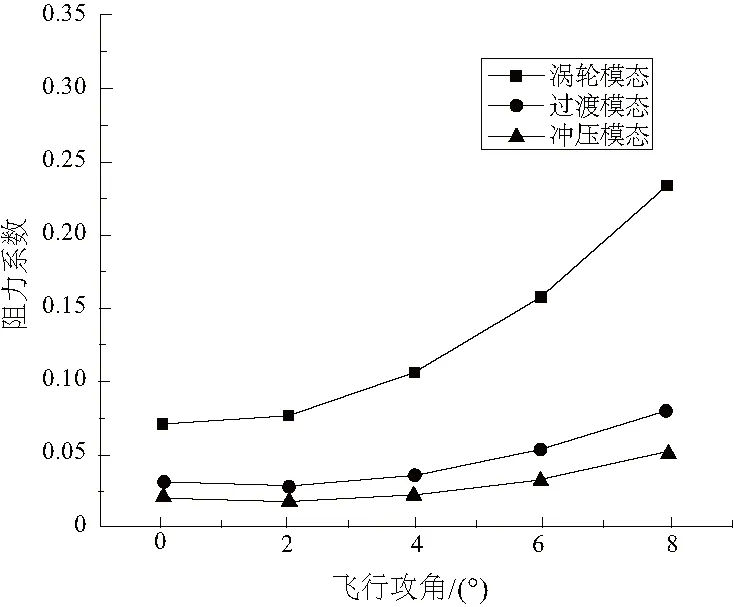
图15 阻力系数曲线

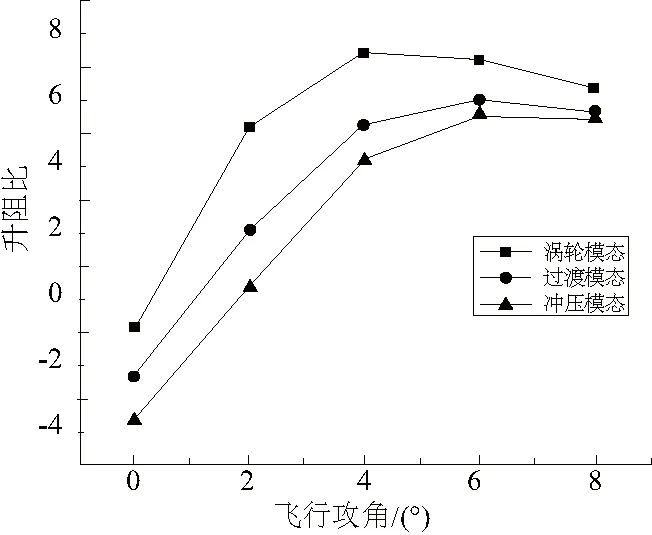
图16 升阻比曲线

本文飞行器一体化设计状态为飞行马赫数5.0时工况，进气道前激波封口，基本不产生溢流；喷管出口气流完全膨胀至环境压力，推进效率最高。非设计状态下，飞行器进气道前激波前移甚至脱体，进气道附加阻力增大，喷管出口气流过膨胀，在后体段出现低压区，后体阻力增加。

4.2 部件升阻力贡献影响研究

1)部件升力贡献影响研究

一体化飞行器各主要部件升力对整个飞行器升力的贡献如图17-图19所示。计算结果表明：在三个模态的0°飞行攻角下，飞行器机身面前端上壁面压力高，后端机身上下壁面压力抵消，所以升力贡献均为负贡献，产生低头力矩。在涡轮和过渡模态其他飞行攻角下，前体面和机身面为飞行器提供了绝大部分的升力；涡轮模态下，推进系统面在所有飞行攻角下升力贡献均为负，产生抬头力矩，其余两个模态下，推进系统升力贡献随攻角增大而增大，产生的低头力矩也随之增大。

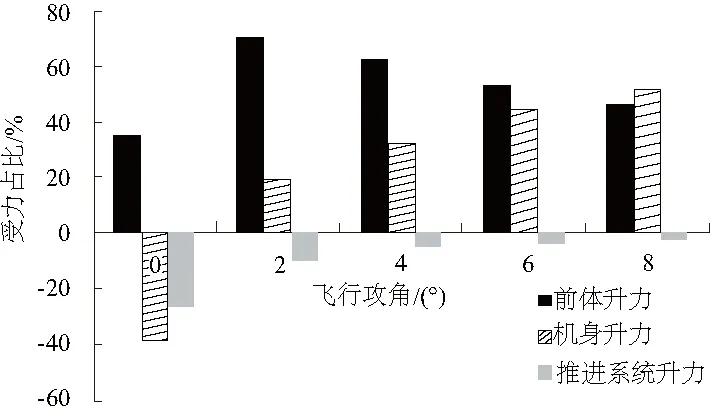
图17 涡轮模态升力贡献

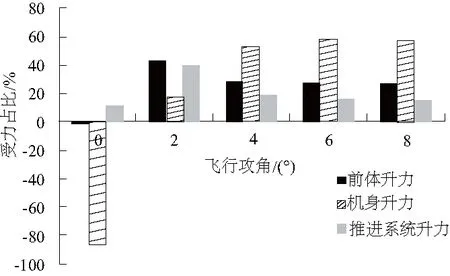
图18 过渡模态升力贡献

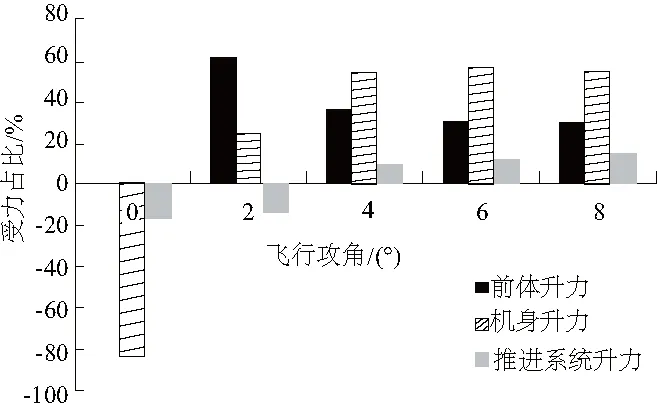
图19 冲压模态升力贡献

2)部件阻力贡献影响研究

一体化飞行器各主要部件阻力对整个飞行器阻力的贡献如图20-图22所示。计算结果表明：高超声速飞行器飞行过程中机身阻力占了总阻力的绝大部分；随着攻角的增加，前体阻力贡献增大；推进系统增量(指推进系统机身法向受力在气流坐标系下的轴向分力)在涡轮模态下随攻角变化趋势不大，推进系统机身法向分力向下，表现为负贡献，抵消一部分气动阻力；在其余两个模态下，推进系统增量随攻角增大而增大，推进系统机身法向分力向上，表现为正贡献，产生附加的气动阻力。

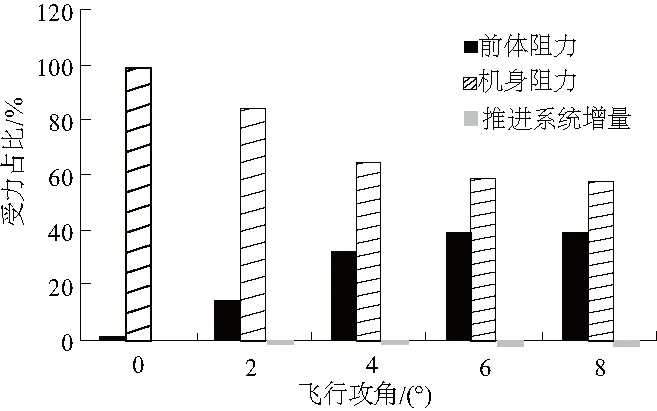
图20 涡轮模态阻力贡献

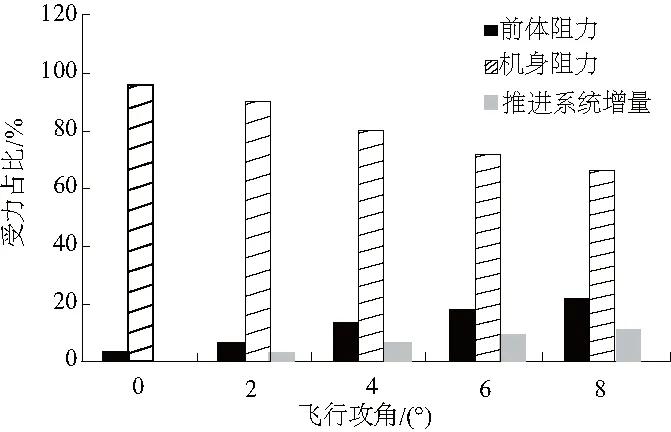
图21 过渡模态阻力贡献

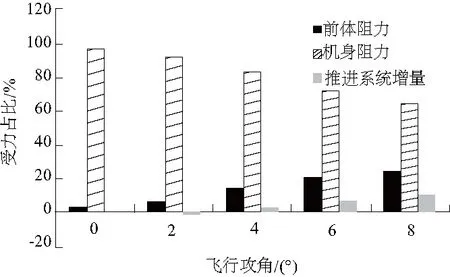
图22 冲压模态阻力贡献

5 结语

本文计力体系主要研究针对理论模型如何划分和计算各项力以及如何结合飞行器数值模型，通过飞行器数值模拟计算结果获得计力体系下各项力数值，通过研究可得到以下结论：

1)由于数值仿真软件在机身坐标系下统计各项力，故可从机身坐标系下对飞行器进行受力分析及气动/推进力公式推导，通过坐标转换得到气流坐标系下飞机升阻力。

2)升力计算通过全机所有面法向力向气流坐标系分解得到；

3)跨声速飞行时(Ma=1.2)，前体部件对全机升力影响最大，前体压缩产生了一个很大的抬头俯仰力矩，使得飞行器纵向静不稳定；过渡模态和冲压模态下，随着飞行马赫数的逐渐增大，推进系统升力和机身升力贡献逐渐增大，逐渐成为影响飞行器升力性能的关键部件；

4)高超声速飞行器机身阻力大小决定着整个飞行器的阻力表现，如何优化机身面，减小高马赫数飞行时带来的阻力影响将持续成为高超声速的一个重要研究方向。