悬挂参数对重载货车车轮磨耗的影响

张浩，李子嘉，戴焕云

(西南交通大学 牵引动力国家重点实验室，四川 成都 610031)

0 引言

为了配合国家煤炭等货物“公转铁”政策的实施，发挥铁路大运量低价格的优势，我国铁路部门近些年来尤其重视重载货运的发展，兴建了一批以大秦铁路和浩吉铁路为代表的重载货运专线，开行万吨货运专列。但是随着列车牵引货物量上升，轴重提高，一系列问题暴露出来。比如轮轨作用力显著上升，导致车轮踏面磨耗加剧，这对列车的动力学性能产生较明显的影响。因此，国内外学者对车辆踏面磨耗的影响因素展开了研究。俄罗斯的ROMEN Y S等[1]通过计算机模拟得出磨耗率与轮轨间摩擦系数和轮径以及锥度之间的关系。CHEN S等[2]考虑温度对车轮材料弹性模量、抗拉强度和硬度等性能的影响，研究了温度对接触片尺寸、黏滑区划分、磨损系数和磨损深度的影响。罗仁等[3]通过仿真对比了Anchard模型和磨耗功模型的各自适用范围。张良威[4]通过研究发现，良好的轮轨匹配可以减轻车轮踏面磨耗。郭金莹[5]建立了30 t轴重货车非线性动力学模型，分析了轴距、旁承摩擦系数等对磨耗的影响规律。杨阳等[6]考虑机车传动系统的影响，研究了不同工况下的机车车轮磨耗情况。PRADHAN S等[7]建立了一个考虑通过曲线时制动和启动工况的模型来估计车轮磨损对轨道车辆动力特性和平顺性的影响。日本学者半田和行等[8]通过台架试验研究车轮磨耗和闸瓦热效应之间的关系。马超智等[9]对摩擦功模型进行了改进，结合轮轨接触处的Mise应力分布特征，得出了较为精确的结论。衣美玲[10]建立了C70货车模型进行仿真分析，得出合理设置超高在减轻车轮磨耗中起到的积极作用。ZENG Y C等[11]提出了一种新的基于物理数据驱动的车轮磨损建模预测平台。TONG L F等[12]认为法向载荷对车轮磨损过程的影响大于滑动速度对车轮磨损过程的影响。TAO G Q等[13]建立了一种考虑轮轨系统固有振动特性对车轮磨损影响的机车车轮磨损仿真模型。

本文着重分析悬挂参数对重载车辆车轮磨耗程度的影响规律，并对重载线路货运车辆动力学性能和踏面磨耗变化趋势进行预测和仿真。本文在分析大量数据后，找到车轮在轮缘区和踏面区的磨耗分布发展规律，并根据这些规律，对30 t轴重重载车辆磨耗发展趋势进行预测，为新踏面设计和站段镟修工作提供重要参考信息。铁道车辆悬挂系统是一个十分复杂的、相互关联的系统，本文主要关注一系悬挂参数对磨耗发展变化的影响，综合考虑各方面因素从而得到最好的轮轨匹配状态，降低轮轨动作用力，优化悬挂参数，提高列车的动力学性能，为今后开行长、大列车奠定良好的基础。

1 车轮踏面磨耗理论模型

1.1 车轮踏面磨耗分析方法

车轮磨耗主要是由材料塑性变形和轮轨材料脱离两种原因造成的。车辆在通过曲线时，运行状态较差，尤其是在轮缘贴靠的情况下，车轮的磨损较为严重，这会破坏踏面的原有形状，对列车运行品质产生不好的影响。实际上，车轮踏面的实时形状和车辆动力学性能是互相影响、互相作用的。

车轮踏面磨耗的仿真计算过程如图1所示。首先结合大秦铁路的实际情况设定车辆、轨道、初始车轮踏面等参数建立车辆-轨道多体动力学仿真模型，通过计算得到的轮轨滚动接触参数并进行分析，然后通过车轮磨耗模型计算踏面磨损，根据所得结果更新车轮踏面参数。再将磨耗后的车轮踏面参数代入到所建立的多体动力学模型中，得到新的磨损踏面参数，通过将这个迭代过程不断重复，最终得到所需的结果。

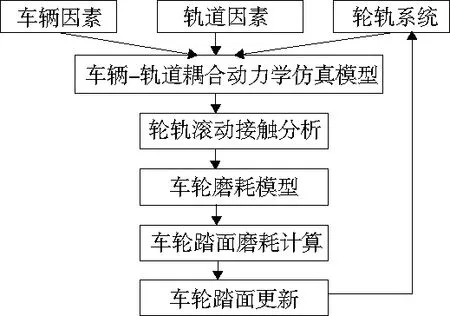
图1 车轮磨耗仿真流程

1.2 多体动力学模型建立

目前国内重载铁路上线运行的货运车辆种类众多，但最常用的主要为C80系列敞车，转向架主要为转K6、转K7型等。本文主要对采用转K6型转向架的C80型重载货车进行研究。在车辆-轨道耦合系统动力学理论的基础上，通过SIMPACK仿真软件建立重载货车的动力学仿真模型，模型包括1个车体，2个转向架，共90个自由度。其中轴箱上8个承载鞍各有一个垂向自由度，而4条轮除有6个自由度以外还有1个弯曲自由度及1个扭转弹性自由度，摩擦减振器处8个斜锲各1个垂向自由度，除此之外的车体均包含6个自由度(3平动+3转动)。基本参数见表1，多体动力学模型见图2。

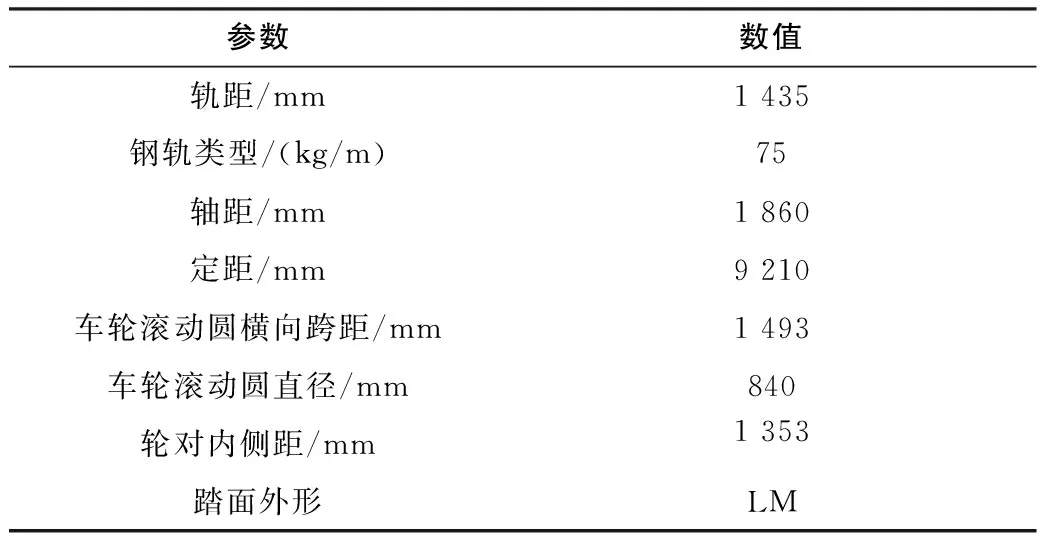
表1 动力学模型基本参数

图2 重载货车多体动力学模型

1.3 轮轨滚动接触模型

本文采用CONTACT轮轨滚动接触计算模型[14]所得到的接触斑数据进行处理。首先计算出接触斑的外形，包括长轴和短轴长度，将接触斑所在区域划分成一定数量的子单元，分别对每个单元上的法向力、蠕滑力、蠕滑率、接触角和接触点坐标进行计算，最后将以上计算结果代入踏面磨耗模型，得到接触斑内的磨耗深度分布图。CONTACT程序采用非赫兹弹性接触算法得到的接触斑外形和应力分布如图3所示。

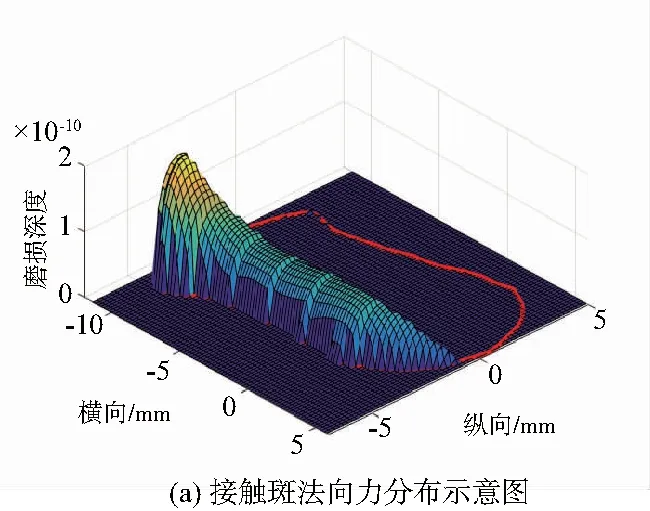
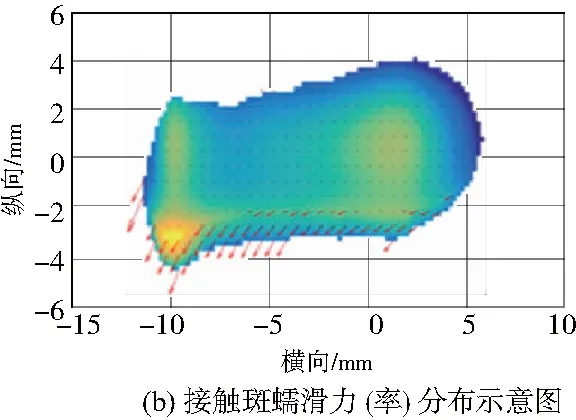
图3 接触斑外形及作用力分布

1.4 车轮磨耗模型

本文选用Archard模型[15]计算车轮踏面的磨耗。这是学术界较为常用的计算磨耗水平的模型之一。假定黏着区内无磨耗存在Archard磨耗模型，一般计算材料磨损体积公式如下：

(1)

式中：Vw为材料磨损的体积，m3；L为轮轨之间的滑动距离，m；N为法向力，N；H为材料硬度，取轮轨中较软的材料硬度，N/m2；K为无量纲的磨耗系数。

将每个接触椭圆小单元中心表达为坐标(x,y),单元的长度为Δx和Δy，可得Herts法向压力分布如式(2)所示。

(2)

磨耗深度Δz如式(3)所示。

(3)

式中：Δl为一个时间增量内的滑动距离，m；pz为轮轨接触斑法向压力，N；K与H含义同上式。

2 仿真数据分析

2.1 一系(轴箱)纵向定位刚度(Kpx)对轮轨作用的影响

通过对不同一系纵向定位刚度下的部分货车轮轨作用进行动力学指标的计算，其中直线工况为运行速度80km/h，曲线工况为半径500 m(参考大秦线最小曲线半径)，运行速度60km/h，得出结果如图4所示。

如图4(a)所示，在直线工况下，4根车轴的轮轴横向力随着一系纵向定位刚度的增大而减小，动力学安全性指标趋于变好，右轮的轮轨横向力有着类似的变化趋势。从磨耗功率均值来看，直线运行时车轮的磨耗随一系纵向定位刚度的变化缓慢增大。

如图4(b)所示，在曲线工况下，4根车轴的轮轴横向力随着一系纵向定位刚度的增大而缓慢增大，右轮作为外侧轮，轮轨横向力在变大，其中1轴的变化最明显，2轴、3轴变化较小，4轴变化略大。从磨耗功率的角度来说，右轮的磨耗功率大于左轮，而且呈现近乎线性上升的状态。

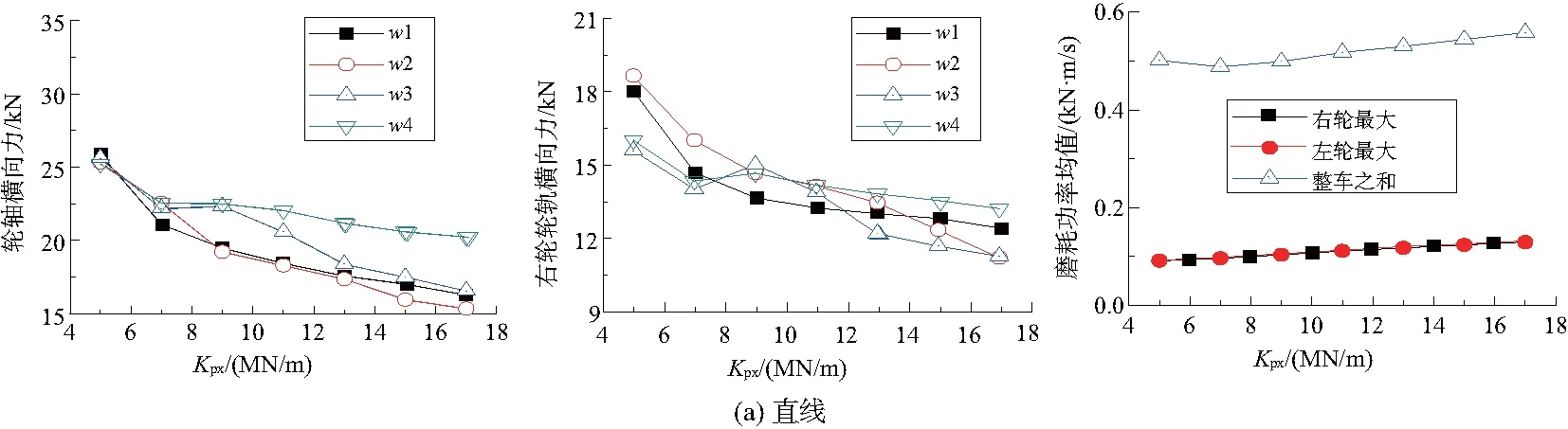
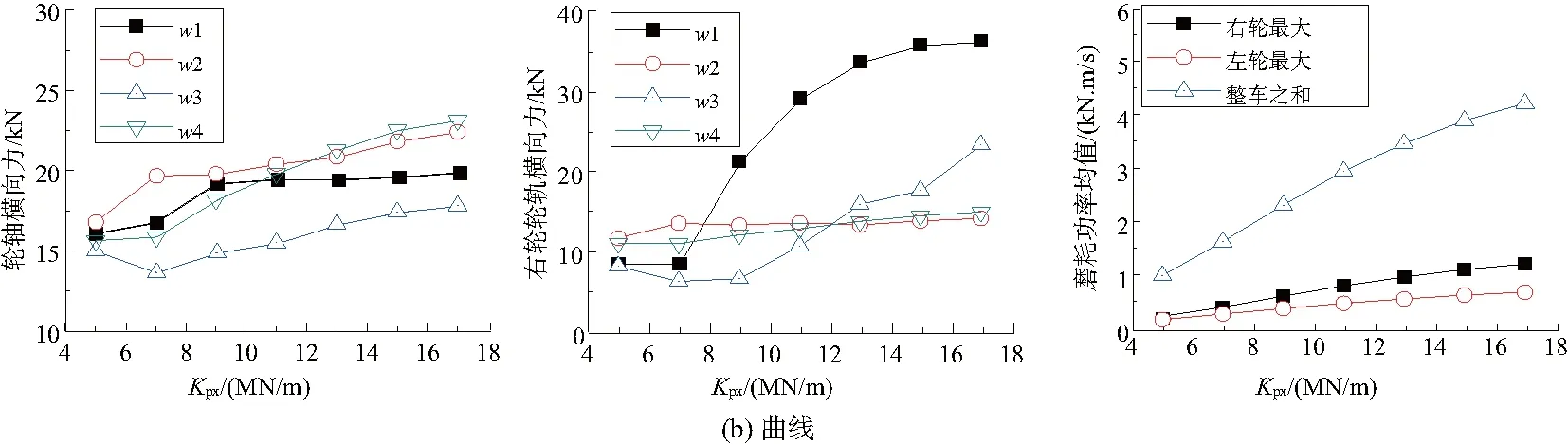
图4 Kpx对轮轨作用的影响

综合考虑车辆运行的两种工况，可以发现一系纵向定位刚度处在7 MN/m时，轮轴横向力变化和右轮轮轨横向力趋于稳定，且左右轮磨耗功率平均值差距最小，产生的轮径差也最小，接下来采用Anchard磨耗模型对该刚度下的磨耗情况进行进一步的分析。

2.2 一系(轴箱)纵向定位刚度(Kpx)对踏面磨耗的影响

影响车轮磨耗的悬挂参数主要包括一系垂向挠度、旁承摩擦系数、斜楔主摩擦面摩擦系数以及一系定位刚度(横向、纵向)等。

本文主要研究一系纵向定位刚度对车轮磨耗深度指标的影响，从而对车轮的磨耗进行较详细的研究。分别考虑车辆在直线与曲线上运行时，轴箱纵向定位刚度从5 MN/m变化到17 MN/m，步长为2 MN/m时，一位轮对车轮磨耗分布区域的位置和大小以及磨耗深度的变化规律，仿真结果如图5所示。其中，曲线半径设置为500m，车辆运行速度为80km/h。

从图5可以非常直观地看出，随着一系纵向刚度的增加，车轮磨耗深度的整体趋势是在逐渐增大。在直线轨道上，一位转向架车轮型面磨耗深度平稳增大，左、右轮的峰值差距不太大，且峰值所处位置均在5mm附近。在曲线轨道上，右侧轮的磨耗量随一系纵向刚度增大急剧增加，而且峰值和磨耗区域向轮缘处靠近，左侧轮磨耗量随一系纵向定位刚度增大平稳上升，但是磨耗量较右侧轮要小，磨耗区域处于-10mm～16mm的远离轮缘区的位置。

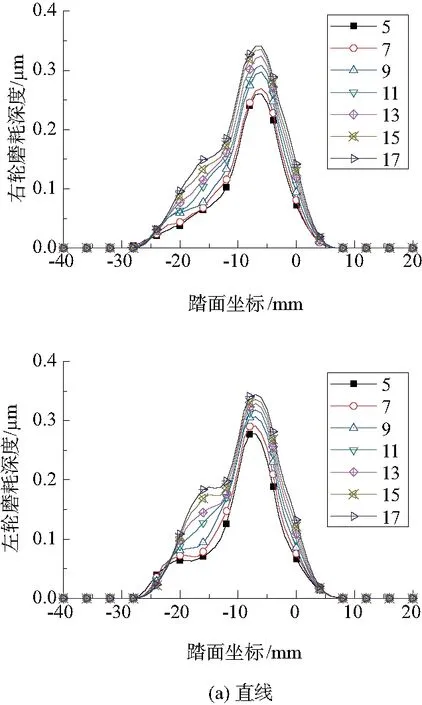
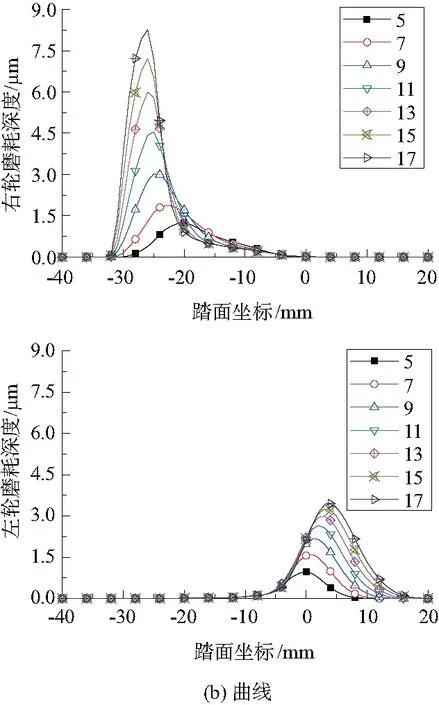
图5 Kpx对一位轮对磨耗的影响

由图6可知，左、右轮最大磨耗深度差随一系纵向定位刚度的增大而迅速增大。因此，在较大的一系纵向定位刚度情况下，曲线通过时产生的横移会加剧右侧车轮的磨耗进程，同时左侧车轮的磨耗速度较为缓慢一些。在车辆运行较长时间后，同一轮对的轮径差会逐渐变大，影响车辆运行的稳定性，所以在镟修时，要针对不同的磨耗情况，将其修正为正常踏面形状。

图6 通过曲线时左、右车轮磨耗深度差

根据图6可得在5 MN/m和7 MN/m时左右轮的磨耗深度差是最小的，但考虑控制构架在纵向振动加速度幅值，7 MN/m为较好的选择。图7为一系纵向定位刚度为7 MN/m时的一位轮对磨耗分布曲线。在这种情况下，通过曲线时左、右轮磨耗量接近，而且磨耗区域差距不大。此时，车辆在曲线通过时产生的轮径差较小，列车运行更加平稳。

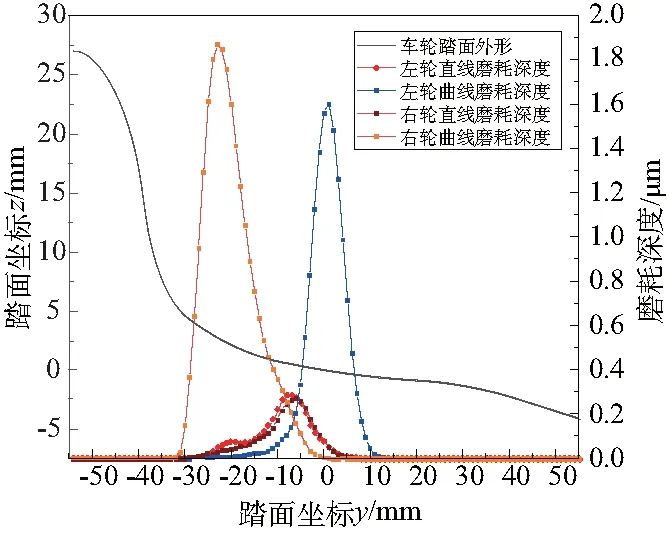
图7 一位轮对两种工况下磨耗曲线

3 结语

1)随着一系纵向刚度的增加，曲线工况下的轮轴横向力、右轮(外轮)轮轨横向力以及磨耗功率平均值均增大，1轴变化较为明显。各项指标在7 MN/m后变化速率发生变化。

2)车轮的磨耗增大且曲线上左、右两侧一位轮对发生磨耗的位置与深度相差较大。因此在设计转向架一系纵向定位刚度时，在满足临界速度且有足够稳定余量的条件下，需要选择尽可能小的刚度值，7 MN/m左右较为合理。