基于并联RSO优化自抗扰的PMSM速度控制

付文强，赵东标，刘凯，赵世超

(南京航空航天大学 机电学院，江苏 南京 210016)

0 引言

永磁同步电机结构简单，功率密度高，已被广泛应用于各个领域[1]。由于其是一个强耦合、多变量的复杂系统，使用传统的PI控制很难提高其调速性能。随着控制理论的发展，越来越多的非线性控制方法被提出，如鲁棒控制[2]、滑模控制[3]、无源控制[4]、自抗扰控制[5](ADRC)等。

ADRC结合了现代控制理论和经典PID控制的优点。ADRC主要由跟踪微分器，误差反馈控制律和扩张状态观测器组成[6]。扩张状态观测器是ADRC的核心，其可以对扰动进行观测[7]。控制器通过对观测的扰动进行补偿将控制对象转化为积分串联型系统[8]。但是，状态观测器的观测精度容易受到扰动量的大小和带宽的影响。文献[9]提出了一种最小二乘支持向量机优化ADRC的方法，取得了良好的控制效果。

为了提高PMSM调速系统的速度精度和鲁棒性，本文提出了一种基于并联降阶状态观测器优化线性自抗扰控制(LADRC)的方法，不仅保留了线性自抗扰参数易整定的优点，还提升了控制器的抗扰动能力，增强了系统的鲁棒性。仿真结果表明，该方法能够提高系统的速度精度和抗干扰能力。

1 永磁同步电机数学模型

对于PMSM的研究，常有以下假设[10]：1)忽略磁路饱和效应；2)忽略磁滞和涡流损耗；3)磁场空间呈正弦分布。在d-q轴系下得到如下表达式：

(1)

式中：id、iq为定子绕组在同步旋转坐标系下的电流分量；ud、uq为定子绕组在同步旋转坐标系下的电压分量；Rs、Lq、Ld分别为定子的电阻和电感；ωm为转子的机械角速度；Ψr为转子永磁磁链；np为极对数；J、B分别为转动惯量和阻尼系数；TL为负载转矩。

对于隐极式PMSM，d轴和q轴的绕组电感相等，代入式(1)，可以得出其运动方程如下：

(2)

式中J∑为等效转动惯量。

2 传统线性ADRC速度控制

对于式(2)，将电机的运动方程简化为

(3)

式中：u=iq；a(t)=-(TL+Bωm)/J∑；b=1.5npΨr/J∑；a(t)视为系统的总扰动。

针对式(3)所示系统，跟踪微分器可以用一阶惯性环节代替，其表达式如式(4)所示。

(4)

式中：v1为跟踪的输入信号；r1为跟踪因子。

该控制器线性扩张状态观测器的数学模型为

(5)

式中：z1为ωm的跟踪值；z2为扰动的观测值；β01、β02为增益系数。

经过对扰动的补偿可以将系统转换成一个积分环节，采用比例控制律就可以实现很好的控制。针对式(3)所示系统的反馈控制律表达式如下：

(6)

式中k1为比例调节因子，和系统的带宽有关。

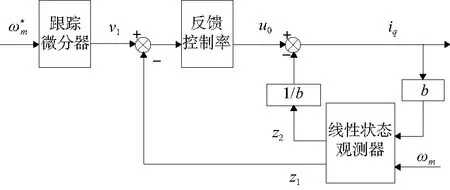
图1 速度环线性自抗扰控制器结构

3 并联降阶状态观测器速度控制

3.1 降阶状态观测器设计

式(5)中，线性状态观测器不仅观测了扰动值，还对速度ωm进行了观测。实际上反馈的速度信号可以利用传感器检测，观测的速度可能受到噪声以及观测器带宽的影响。因此，可对上述扩张状态观测器进行降阶处理。

首先建立式(3)所示系统的状态方程，设x1为ωm的状态变量，x2为a(t)的状态变量，得到其状态方程如下：

(7)

由于x1已知，x2未知，构建出如下降阶观测器：

(8)

式中β03为观测器的带宽。

(9)

式(9)中含有x1的微分项，微分项的引入往往对噪声特别敏感，为此采用间接的方法对上式进行变换。定义一个新的状态变量x3=x2-β03x1，定义其状态估计值为z3，将式(9)简化得到：

(10)

式(10)完成对系统扰动a(t)的估计，且不含速度的微分项，不会放大噪声，具有更好的适应性。所得到降阶状态观测器的结构如图2所示。

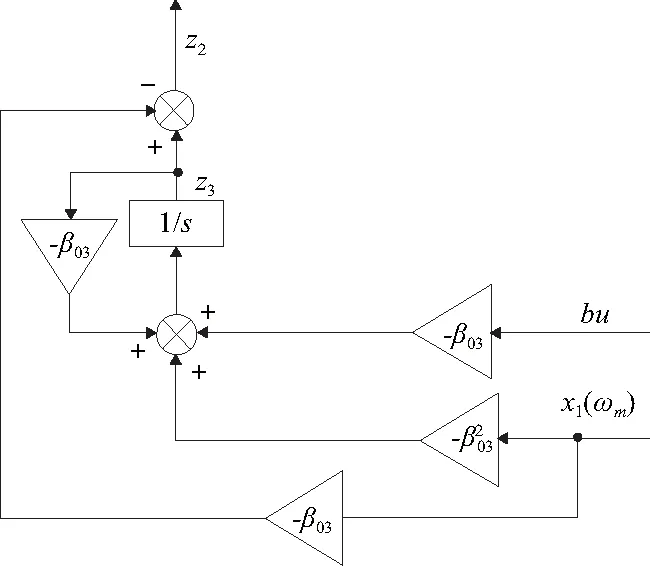
图2 降阶状态观测器结构图

反馈控制率仍采用线性比例控制：

(11)

式中k2为比例系数，和系统带宽有关。

定义误差e4=x2-z2，由式(7)和式(9)可得降阶状态观测器的误差状态方程如下：

(12)

式(12)的特征方程为det(s)=s+β03。因此，只要β03>0，同时扰动项a(t)有界，那么降阶状态观测器就是稳定的[11]。

3.2 速度控制器设计

当扰动幅值较大时，会存在一定的观测器误差[12]。假设系统总的扰动a(t)中存在观测器误差f′，则有

a(t)=z2+f′

(13)

为了消除观测器误差带来的影响，在原控制系统中并联一个RSO，用于对误差f′进行观测。

因为金钱制度的结果，弄得人类境遇不济，又因为须传种的缘故，不得不有家族制，又渐渐的进到国家制度，作为保障，这种无谓的保障，不但无益，还是有害。家族底制度，统是首领制，或包头制；这种制度，名为拥护人类，其实统以经济的眼光，去对待人类罢了。家人因为家主是养活我们的，便予以无上的威权；家主因为家人是他养活的，所以就看轻他。家主既有无上的威权，当然就要负保养家人完全的责任；家人也就自卑自弃的堕落他的本能，作非人生的事；如子弟不事生产，家居作乐，于是滥事消费，繁滋生殖，不但弱小人种，还要堕落本能，代代相传，哪有不穷？这是最明确的证据，余的还有，也说不完。

由式(3)和式(11)可知，系统通过补偿得到理想的积分型系统，若观测器存在误差f′，则有

(14)

(15)

式(15)和式(7)相似，只是式(15)观测的是系统与理想积分型之间的误差，实现对观测器误差进行实时的观测。根据以上对降阶观测器的设计，得到对f′观测的降阶状态观测器方程如下：

(16)

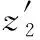
(17)

式(17)完成了对f′估计，对此，反馈控制律的设计也做出相应的修改：

(18)

将式(18)所示控制律代入式(3)就得到了更为精确的纯积分系统。为了减少反馈速度噪声对观测器的干扰，将反馈信号也增加一个跟踪微分器，不仅能够对噪声进行滤波处理，还能消除反馈信号与输入信号因跟踪微分器所带来的相位滞后。所设计的速度控制器需要整定的参数为：r1、β03、β04、k2，其中β03=β04，为降阶状态观测器的带宽。该速度控制器结构如图3所示。

图3 并联降阶状态观测器速度自抗扰控制器结构

根据以上设计，电流环采用PI前馈解耦控制。可以得到本文设计的速度控制结构如图4所示。

图4 PMSM速度控制系统框图

4 仿真试验

为了验证所设计控制策略的有效性，在Matlab/Simulink中分别搭建如图4所示的本文所设计的控制系统、传统PI控制的调速系统以及传统线性ADRC调速系统，进行仿真对比研究。本文研究的对象是飞机应急电源地面模拟试验台的驱动电机，该驱动电机的具体参数如表1所示。

表1 电机参数

1)速度跟踪仿真试验

该仿真试验策略如下：在电机空载的情况下，设定初始参考速度为3 000r/min；在1s时将参考转速设定为6 000r/min；在2s时，将参考速度突降为4 000r/min；在3s时，将参考转速下降为1 000r/min。得到仿真结果如图5所示。对比图5(a)与图5(b)可知，采用PI控制时，速度跟踪存在一定的超调，超调量最大可达2%；而采用线性ADRC或是本文设计的控制算法，可以实现无超调跟踪。结合图5(a)和图5(b)的稳态速度放大图可以看出，本文设计的控制算法和传统线性ADRC控制算法稳态速度精度都比PI控制要高。在低速时，如图5(b)中1 000r/min，本文控制算法具有更小的稳态误差。

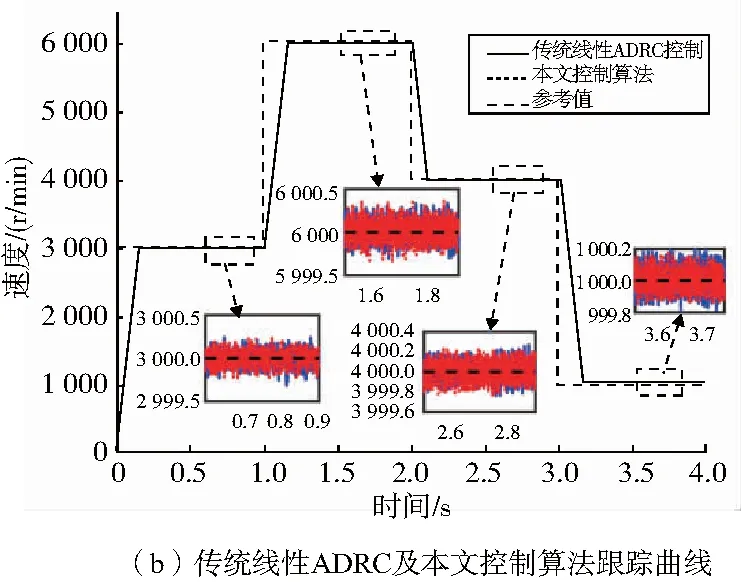
图5 速度跟踪曲线

2)负载突变仿真试验

为了验证控制策略在负载突变时的适应性，设计如下仿真试验：电机空载启动，设定稳态转速为6 000r/min；当电机达到稳态转速后，在1s时突加160N·m的负载转矩；转速达到稳定之后，在2s时，将载荷卸去，得到系统的速度响应曲线如图6所示。表2和表3为速度超调量和稳态误差的计算值。

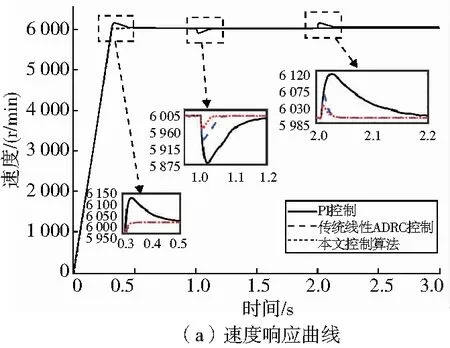
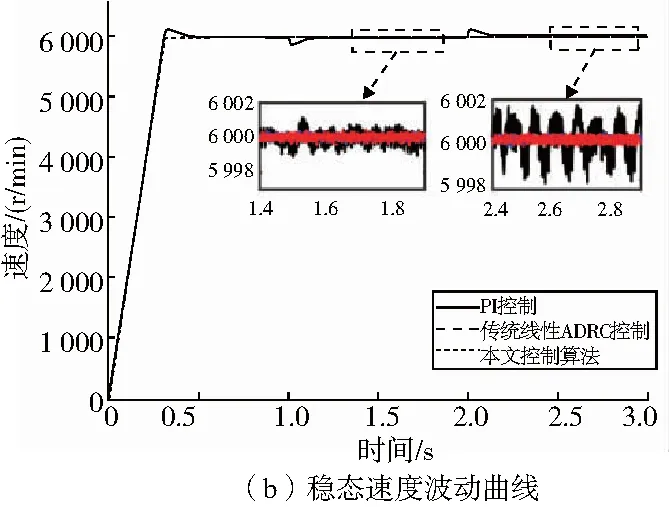
图6 突加突卸160N·m负载时速度响应曲线

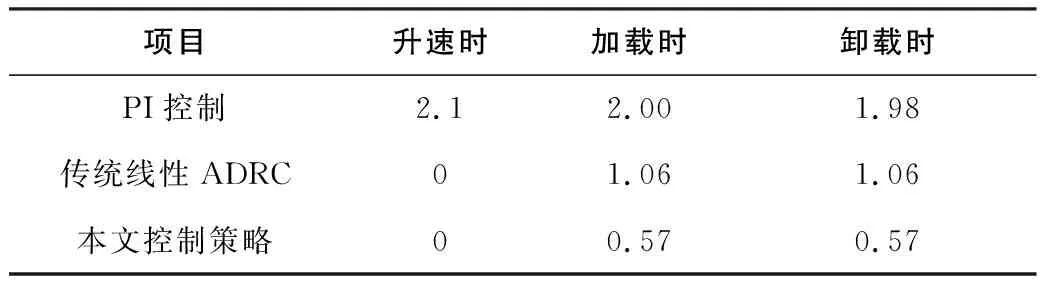
表2 速度超调量 单位：%

表3 稳态速度精度 单位：%

由图6(a)可知，采用传统PI控制，无论是加速到稳定转速，还是突加突卸载荷时，速度超调量都特别大。表2显示，PI控制的超调量最大达到2.1%。而ADRC控制在转速上升的时候几乎没有超调，但是相比较之下，传统线性ADRC在负载突变时超调量明显大于本文所设计的控制策略，传统线性ADRC在负载突变时速度超调量达到了1.06%，本文控制策略速度超调量仅为0.57%。这是因为负载突变产生的扰动较大，对于传统线性ADRC，其观测器受到带宽的限制，容易受到扰动幅值的影响；而本文设计的速度控制器采用两个降阶的观测器，在保证带宽的情况下还可以观测出观测器的误差，能够提高控制系统的抗干扰能力。同时，可以看出在负载扰动产生之后，PI控制器回复时间最长，其次是线性ADRC控制器，然后是本文设计的控制器，说明本文设计的控制器能够加快系统受到扰动之后的回复速度。图6(b)反映的是在负载突变达到稳定之后速度稳态精度，可以看到，PI控制的稳态误差最大，可达 0.033%。传统线性ADRC和本文设计的控制策略稳态速度波动都相对较小。

5 结语

线性ADRC控制器可以不依赖于准确的数学模型，对系统的扰动进行观测和补偿。但是线性状态观测器容易受到带宽的限制，影响系统的抗扰动性能。采用并联降阶状态观测器的方法，不仅保留了线性状态观测器参数易整定的优点，同时还提高了系统的鲁棒性。仿真结果表明：

1)采用并联降阶状态观测器能够提高系统的稳态速度精度；

2)使用本文提出的控制算法，系统具有更强的鲁棒性，受到扰动之后，能够更快达到稳定。