不同轮对组合的转向架动力学性能分析

孔振文，周文祥，祝向阳

(西南交通大学 牵引动力国家重点实验室，四川 成都 610031)

0 引言

传统车辆稳定性和曲线通过性能的不兼容一直是轨道车辆难以避免的问题[1]。随着车速的高速化和线路的复杂化，这个问题愈发突显。独立轮对(IRW)理论上可以完美兼顾两种特性，然而其结构本身缺乏自导向能力[1]。在此基础上，众多相关学者对新型导向单元进行了长期的探索[2]。

1950年，西班牙Talgo转向架的问世，被视为新型导向单元的成功开发案例。此后，德国、日本相继尝试开发了EEF、EDF和RT-X1转向架[2]。这些导向单元的设计思想，都是借助轮轨间作用力产生稳定的复位力矩，尤其是借助重力复原力。在国内，新型导向单元的研究相对较少，主要集中于径向转向架开发[3]、磨耗踏面设计[4]和主动导向控制[5-6]的研究。前两者采用的都是机械的方法，普适性不足，而后者理论上存在更好的可能性。主动导向控制最早成熟于汽车行业[7]。国内有关铁路车辆主动导向控制的研究起步较晚，任利惠教授较早研究了独立轮对的主动控制技术。

新时期背景下，对下一代高铁设计[8]的稳定性和曲线通过性能有了更高的要求。为此，本文借助传统刚性轮对和独立轮对的不同特性，分析二者组合的转向架动力学特性，为新型导向单元的设计提供参考。同时，对IRW的组合转向架提出一种简单可靠的主动导向控制方法。

1 动力学方程

对于两轴转向架，刚性轮对(SW)和独立轮对(IRW)的不同组合会呈现不同的动力学性能。不同轮对组合的转向架形式见表1。

表1 不同轮对组合的转向架形式

为方便研究车辆动力学相关问题，本文只考虑车辆系统的平面运动，忽略一、二系垂向悬挂的影响，忽略轨道激励的影响。

综上所述，刚性轮对、转向架和车体均只考虑摇头和横移两个方向的运动，独立轮对还需要考虑左、右车轮的相对旋转自由度，表达式推导如下：

刚性轮对：

(1)

独立轮对：

(2)

转向架:

(3)

车体：

(4)

式中：y、ψ、φ和ε分别为横移、摇头、侧滚和左右车轮差速之半，其一阶倒数和二阶导数分别为速度项和加速度项，下标w、b和c分别代表轮对、转向架和车体，k=1～2和i=1～4分别代表转向架构架和轮对以及对应线路的编号；Kg、Kθ分别为重力刚度和角刚度，且Kg=Pλe/a,Kθ=Pλea，P为轴质量；K、C分别为刚度和阻尼，下标p、s分别代表一系、二系悬挂，x、y为方向；f11、f22分别为纵向和横向蠕滑系数；λe为轮对踏面等效锥度；r0为滚动圆半径；R为曲线半径；θ为外轨超高角；a为车轮滚动圆横向跨距之半；b、c分别为一系、二系悬挂横向跨距之半；lb和lc分别为轴距和车辆定距。

2 动力学分析

2.1 稳定性

车辆临界速度就是蛇行运动临界速度，指车辆系统在一定条件下发生周期蛇行运动对应的最低车速[9]。按照李雅普诺夫稳定性的概念，可根据车辆系统的状态系数矩阵(雅克比矩阵)特征根的变化进行求解。当特征值存在正实部或者存在零重根时，系统不稳定，其值为车辆系统线性临界速度。

为简化计算，假定车辆为绝对参考，不同轮对组合的转向架自由度为6-8阶，对应的状态系数方程为12-16阶。按照上述原则，通过上式进行Matlab编程计算，不同轮对组合转向架的线性临界速度如表2所示。

表2 不同轮对组合转向架的线性临界速度

表中Vc为线性临界速度。

为进一步体现不同轮对组合转向架的直线导向能力，设置初始速度为300km/h和一位轮对初始位移激扰为2mm，可以得到不同轮对组合转向架的抗干扰能力，如图1所示。

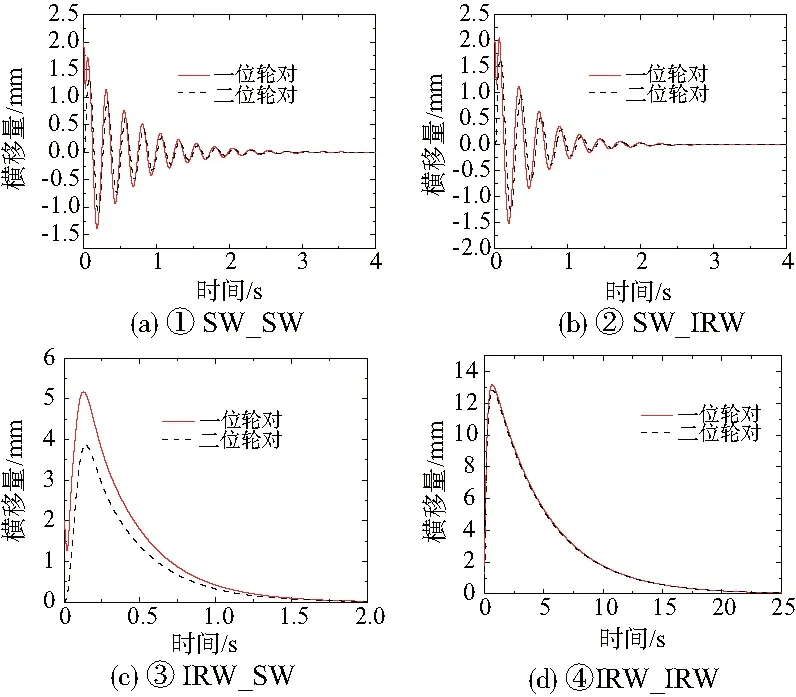
图1 不同轮对组合转向架抗激扰位移-时间图

稳定性评价标准仅考虑线性临界速度，由表2和图1可知，在运动稳定性上，④>③>②>①。带有IRW的转向架的自导向能力比带有SW转向架的自导向能力弱，但抗蛇行振荡行为更好。综上不难判断，独立轮对有助于提高车辆系统的稳定性，且其作为导向轮比从动轮对系统稳定性改善更多，但是会弱化车辆的自导向能力。

2.2 曲线通过性能

两轴转向架过曲线可能会出现较大转角，小角度假设的简化公式不再适用，所以Matlab仿真结果并不理想，故采用Simpack搭建了不同轮对组合的两轴转向架，转向架以30km/h的速度通过半径为1 000m的曲线。以一位、二位轮对的横移量和磨耗指数作为不同轮对组合的转向架曲线通过性能的评价指标，所得结果如图2和图3所示。图3中，稳态值指标为曲线段的中位数。磨耗指数是车轮切向力与蠕滑的标量积，它也等于轮轨摩擦功率与名义速度之商，即：Pf/V。

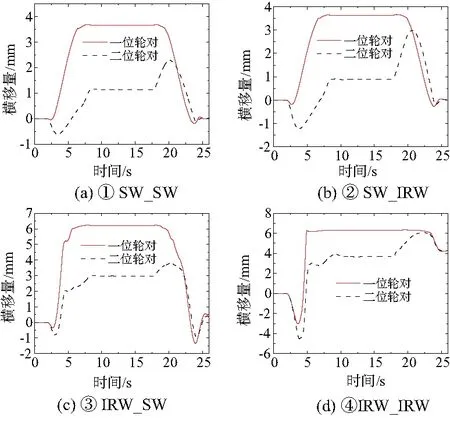
图2 不同轮对组合转向架曲线通过的位移-时间图

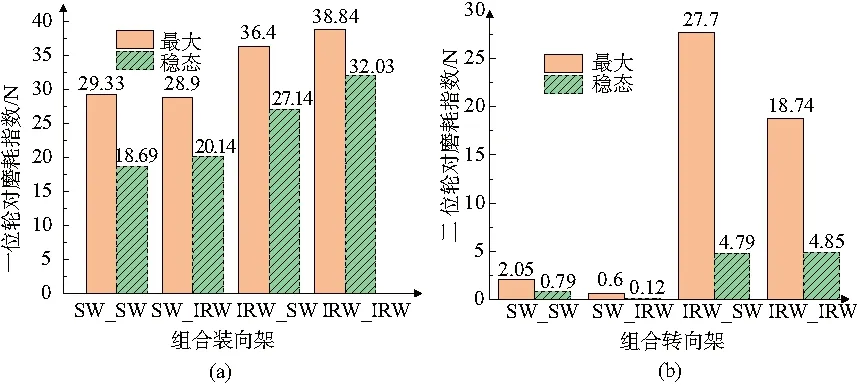
图3 不同轮对组合的转向架磨耗指数图

由图2和图3可知：在曲线通过性能方面，②>①>④>③。需要指出，文中所建模型的轮轨间隙较小，轮对横移5mm时开始发生轮缘接触。从结果可以推断，无控制的独立轮对转向架系统缺乏曲线导向能力，刚性轮对的引入有助于改善车辆系统的曲线通过性能，且刚性轮对作为导向轮比从动轮对曲线通过性能的提升更明显。此外，刚性轮对在前，独立轮对在后的转向架导向性能更好，这表明受导向控制的IRW导向单元具有更好的导向性能。对于较大曲线半径的线路，刚性轮对完全可以满足车辆的曲线通过性能要求。

3 IRW_IRW转向架的车辆主动导向

3.1 导向原理

前述分析表明IRW_IRW转向架的车辆系统在运动稳定性和曲线通过性能方面，都有更好的可能性，尤其是对于小曲率半径的曲线线路。然而IRW_IRW两轴转向架的车辆系统缺乏自导向能力，需要施加额外的导向控制。

本文采用作动器控制，提出一种实用的控制策略，完整的受控制车辆系统平面概念图如图4所示。

图4 带有作动器的独立轮对两轴转向架的车辆平面模型

独立轮对和转向架有关摇头的公式变为：

(5)

(6)

式中：Tψ2k-1和Tψ2k分别代表k位转向架的前、后两个轮对上的作用力，与Tψi等效。

以左、右车轮的转速差作为反馈量，考虑转速和摇头角的变化极性，例如转速大于控制目标时，摇头角负偏转。采用PI控制时，摇头姿态控制输入力矩Tψ可表示为：

(7)

观察式(2)中有关摇头的公式，当轮对在曲线上达到理想稳态时(转向架处于稳态，摇头角速度为0)，忽略惯性力的影响，表达式如下：

(8)

综上所述，当控制目标介于二者之间时，轮对中心位置也处于纯滚线和曲线线路中心线之间，可表述为下式：

(9)

式中kε暂定义为控制目标因子。

3.2 控制器设计

实际曲线线路分为直线段、缓和曲线段和曲线段。对于直线段，可通过摇头姿态控制来间接调节转速为0，实现轮对的自动对中；对于缓和曲线段，可设置跟随曲率变化的转速控制目标，理想的控制目标信息如下：

(10)

式中κ(s)为缓和曲段曲率随缓和曲线段里程的变化公式。

为避免作动器输出力持续异常输出，导致车辆系统失稳，对作动器增设监测控制器，IRW车辆系统控制概念图如图5所示。

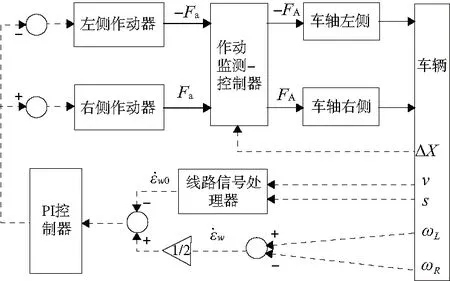
图5 IRW车辆系统控制概念图

由于车轮惯性力很小，忽略高阶项，作动器输出力Fa，一系悬挂纵向力Fpx和轮轨纵向蠕滑力Ffx构成一个平衡力系。当作动器工作时，系统稳定性发生破坏。作动器需要克服一系悬挂纵向力和轮轨纵向蠕滑力作用。蠕滑力极限值等于轮轨最大静摩擦力。因此，作动器输出力为

|Fa|=|Fpx|+|Ffx|≤|Fpx|+Qgμ

(11)

式中：Q为轮质量；μ为静摩擦系数。

基于对作动器输出力设限的思想，可根据作动器输出力工作阙值和车轮打滑两方面进行监测控制。暂不考虑前者，由于外轨超高等线路参数和车辆悬挂力等车辆参数的变化，会引起轮质量减载，轮轨蠕滑力极限值从而减小。为避免蠕滑力超限，发生车轮打滑现象，需折减蠕滑力极限值，安全系数n暂设为1.25。

由于Fpx的阻尼力很小，所以只考虑一系悬挂纵向刚度作用力。由于此监测并非用于精确控制，只为限制车轮打滑，所以对于传感器的精度要求不是很高。已知一位导向轮对的Δx1大于其他轮对的相对位移Δxi，为减小成本，只取一位轮对左侧车轮与转向架一系悬挂连接点的相对位移Δx1L作为监测反馈量，作动器监测-控制器的输出力可表述为：

(12)

3.3 仿真分析

以IRW_IRW的车辆系统以60km/h的速度通过300m的曲线线路为例。采用随机法选择最优控制增益，即在选定最优比例控制增益的基础上，选择最优积分控制增益。所得结果如图6所示，最优比例控制增益Kp取106Ns/rad，积分控制增益KI取8×106N/rad。

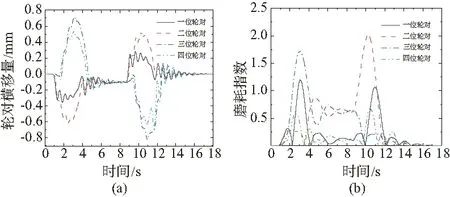
图6 kε=1时最优控制增益下的特征参数

由图6可知，受控制的IRW车辆系统在曲线段近乎趋于线路中心，磨耗指数很小，具有良好的导向性能。此外，作动器输出力大，输出功率非常小，输出力最大值为39.58 kN，最大输出功率仅为40.87 W。这表明控制过程中状态波动小。作动器输出力数值上近似等于一系纵向刚度作用力，其值为39.56 kN，这表明作动器输出力大小主要受一系纵向刚度影响。

一位轮对为导向轮对，所有特征指标通常最大。为便于对比，取最优控制增益下不同控制目标因子kε中一位轮对的横移量和磨耗指数比较，结果如图7所示。

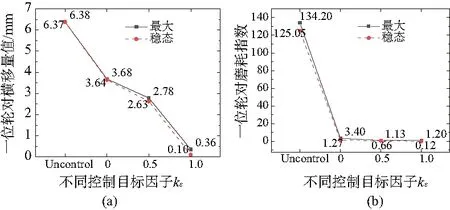
图7 最优控制增益下不同控制目标因子的影响

由图7可知，一位轮对横移量随控制目标因子kε的增大而减小，但非线性变化。

4 结语

综上所述，可得如下结论：

1)在直线稳定方面，④>③>②>①。独立轮对有助于提高车辆系统的稳定性，且其作为导向轮，比从动轮对系统稳定性改善更高，但是会弱化车辆的自导向能力。

2)在曲线通过性能方面，②>①>④>③。刚性轮对有助于改善车辆系统的曲线通过性能，且刚性轮对作为导向轮，比从动轮对车辆曲线通过性能的提升更明显。受导向控制的IRW导向单元的导向性能更好。对于较大曲线半径的曲线线路，刚性轮对完全可以满足车辆的曲线通过性能要求。

3)文中所提的控制方法具有良好的导向控制效果。而且，轮对横移量随控制目标因子kε的增大非线性减小。