基于分形算法的计算机音乐研究

苏飞

(商洛学院， 艺术学院， 陕西， 商洛 726000)

0 引言

机器情商是计算机情感计算研究目标之一，其中最重要的一个方面就是使得机器具备人工创造力。人工创造力是指基于计算机系统的能力，它可以自主地开发某种东西，也可以帮助人类实现想象场景。

20世纪二三十年代，约瑟夫·席林格对音乐进行了最严谨的数学研究，指出节奏可以通过分数来描述，音高可以用实数表示，和弦可以用整数相加表示。以此为契机，借助计算机编程与数学的音乐创作开始蓬勃发展。这些类型的音乐作品通过算法构成，被普遍称为“分形音乐”。可以说，分形音乐是运用分形数学，通过计算机编程而成的音乐作品。

随着人文学科的计算模型不断发展，在艺术领域，尤其是音乐，众多学者研究了许多自动音乐创建模型。早期，由于技术受限，且声音渲染还很初级，众多学者将一些非线性模型应用于复杂音乐的创建，例如基于遗传算法[1]、基于基因的作曲家算法[2]和智能集群算法[3]。后来，随着计算机技术不断成熟，也有不少国内外学者利用噪声[4-5]、语义和语法[6]、推理[7]、智能体[8]等方法创建复杂的音乐模型。

尽管在分形音乐领域已经且取得众多研究成果，然而很少有学者研究如何根据听众的情绪反应来创作分形音乐。另外，一个补充的问题是如何准确预测激发电脑创作音乐的情绪。值得注意的是，第二个问题涉及到将一首新音乐根据情感进行分类。Gregory等[9]指出了音乐特征与情绪之间的关系，指出主调、不协调的旋律和快速节奏与更快乐的反应相关，而它们各自的对立则与悲伤的反应相关。Vincent等[10]介绍了时频散射概念，结合基于光谱时间调制模型，为音频纹理的建模提供了新的思路，然而算法没有考虑人的感情因素。Gregory等[11]研究了一个以人的判断、评价、识别和情感为中心的交互式音乐创作系统，实现了利用遗传算法将人类情感融入到分形音乐的创作中，然而系统没有考虑情绪反应评估与音乐片段之间的内在联系，使得情绪与音乐创作算法之间成为2个孤立的过程。

为了有效解决上述问题，本文在探索了情绪与分形音乐内在联系的基础上，提出了一种利用情绪反馈机制指导分形音乐创作过程的改进分形算法，实现了分形音乐作品的创作和分类任务。该算法主要包含2个过程：①聚类过程，可以按照要求生成新的分形音乐；②预测过程，可以预测产生的分形音乐对听众施加了哪些情绪。

1 基于情绪的分形音乐创作

本节将探索情绪与分形音乐创造过程中的内在联系，旨在探索利用情绪指导分形音乐创造。

正如前文所述，音乐片段可用数学模型表示为式(1)：

p={{R},{F}}

(1)

其中，R表示递归非线性系统特征，F表示音乐特征。进一步，用fi表示特征向量，则具有M维特征向量的音乐片段可表示为式(2)：

p={f1,f2,…,fM}

(2)

其中，i∈[1,M]。用表示音乐片段集合，具有n个音乐片段的音乐集描述为式(3)：

D={p1,p2,…,pn}

(3)

音乐片段产生可通过洛伦兹方程(式(4))获取，即：

(4)

其中，x,y,z,σ,r,b表示系统的初始条件。注意可通过改变其值，从而产生不同的轨迹方程。

进一步，结合方程式(2)，洛伦兹方程下各音乐片段pl描述为式(5)：

pl={x,y,z,σ,r,b,t,l,h,j}

(5)

其中，x,y,z,σ,r,b与式(4)保持一致，t为时间片段，l为乐器，h为和弦，j为音阶。

由式(3)创造的音乐片段pl构成的集合定义为Dl。因此，可用过将任意pl∈Dl与特定情绪相关联，探索pl中音乐片段特征，从而创造出与pl类似的音乐片段。

2 聚类过程

结合第2节相关概念，为音乐片段赋予情绪标记，并创建类似情绪音乐可通过图1所示的群智能方法获得。具体过程描述如下：首先通过聚类器获取原始聚类，其次通过信息融合对原始聚类进行改进，再次根据有效性指标选择最佳聚类，最后得到每个输入特征的随机参数值。

图1 根据情感要求自动创作音乐作品的具体过程

2.1 聚类模型

聚类是将一个集合分成由类似的若干对象组成的多个类的过程，常用方法包括K-means方法、HAC层次凝聚聚类法、最大最小距离聚类算法等。聚类存在2大核心问题，其一是确定最佳分类个数，第二是评估分类的质量。

令D表示由分形音乐构成的集合，π(D)表示对分形音乐集合的聚类操作，最终聚类形成各个子集称为簇，记为C。结合式(2)，∀Ci∈π(D)为m个相似目标p构成的唯一集合。进一步，原始聚类π(D)为一组不想交簇构成的集合，且存在式(6)：

π(D)={C1,C2,…,Cj}

(6)

其中，j为簇的个数。

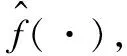
(7)

2.2 选取随机参数

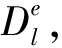
(8)

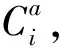
(9)

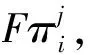
(10)

其中，j∈[1,m]。因此，随机参数选取由融合聚类最优解而得到参数。

3 预测过程模型建立

本节将介绍预测所创建的分形音乐属于何种情绪，如图2所示。具体过程如下。

步骤1：初始化参数，获取m个分类结果，且m>2。

步骤2：在分类器中训练数据集D。

步骤3：计算评估结果与正、负样本的交叉熵以及F矩阵。

步骤4：更新权重，重复步骤2，直至达到设定阈值，退出。

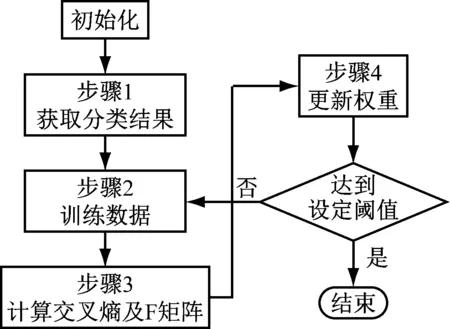
图2 预测过程模型

4 仿真与分析

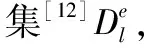
4.1 数据集

本节将介绍创建分形音乐的具体过程。首先，根据式(5)，部分带有标签的分形音乐各参数如表1所示。为简化计算，本文选取时间片段t为固定步长，取t=1。需注意参数乐器l、弦h、音阶j、初始参数(x,y,z)以及洛伦兹方程的变量(σ,r,b)为独立常量，即这些参数不随时间步长而变化；因变量为不同分形音乐所蕴含的情绪标签。

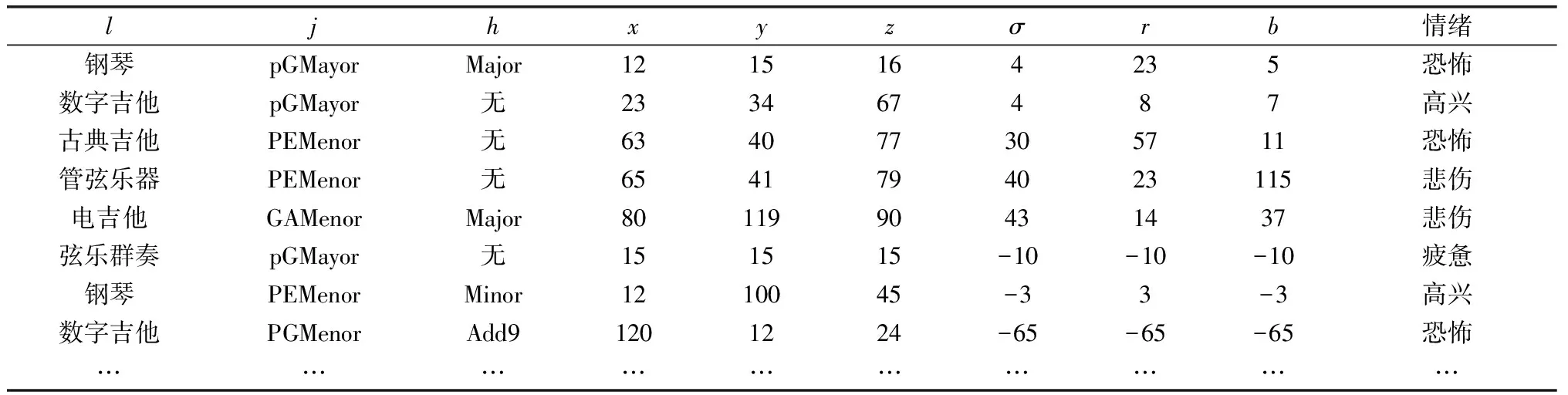
表1 创建分形音乐的部分参数

(1) 创建分形音乐

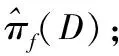
(2) 预测分形音乐

根据第3节预测模型的分类过程，本节设定了一个输出为4的SVM分类器模型，并利用Python进行预训练。本文方法与K-means、HAC层次凝聚聚类法、最大最小距离聚类算法在分类器模型中正确率的对比结果如图3所示。

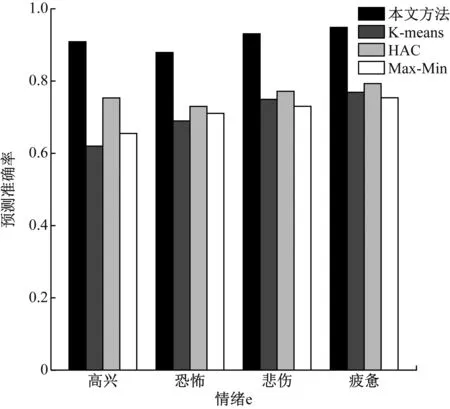
图3 不同聚类方法预测准确率对比

可以看出，K-means方法效果最差。分析原因主要是因为分类时精度不高，导致各簇之间差异不明显。HAC层次凝聚聚类法和最大最小距离聚类算法相比，前者效果稍微好一些。分析其原因，主要是因为最大最新距离在分簇过程中，如果样本差异过大，导致分类结果出现偏差，最终造成预测结果准确率降低。本文方法预测的准确度明显高于其他3种算法，与效果较好的HAC层次凝聚聚类法相比，提升平均正确率约15%。

5 总结

本文提出了一种创建并预测分形音乐的改进分形算法，并对算法执行过程进行了详细介绍。通过仿真分析，结果表明本文提出的方法能够有效创建分形音乐并准确预测。该算法为分形音乐的创建于预测进一步发展提供了一定借鉴和思路。