一类带收获率的捕食者-食饵扩散模型的稳定性

张丽丽， 麻作军

(陇东学院 数学与统计学院, 甘肃 庆阳 745000)

0 引言

自Lotka和Volterra提出经典的捕食者-食饵模型以来，许多学者利用该模型提出了不同的反应函数.在实际生产中，为了兼顾物种的长期存活以及自然生物链的不间断和最大收获，一些学者还建立了带有收获项的捕食者-食饵系统.例如： 1999年， Xiao等[1]对带有常数食饵收获项的捕食者-食饵系统的分支进行了分析，并给出了系统在Bogdanov -Takens分支下的临界条件； 2013年， Gupta等[2]对带有Michaelis -Menten型食饵收获项的捕食者-食饵系统的稳定性和分支进行了分析；其他收获率捕食模型的研究参看文献[3-7].基于上述研究，本文考虑如下带收获率Γh>0的Lotka -Volterra捕食者-食饵模型：

(1)

其中：u(t)和v(t)分别表示食饵和捕食者在时刻t的种群密度；Γ、r、γ和h都是正参数,其具体生态意义见文献[8].

在自然条件及外界因素的影响下，固有有界区域内的不同空间位置上的捕食者和食饵的分布是不均匀的，且每个物种都会有扩散到较小密度区域的自然倾向.为了准确描述种群的这种空间分布的复杂性，一些学者们建立了带有扩散的捕食者-食饵系统[9-12].模型(1)的线性自扩散模型为：

(2)

其中：Ω是RN中边界光滑的有界区域；n为边界∂Ω上的单位外法向量；d1(d1>0)和d2(d2>0)是扩散系数，分别表示2个种群由高密区向低密区迁移；u0(x)和v0(x)为非负不恒为零的连续函数，分别表示2个种群的初始密度.本文讨论模型(2)的正平衡点的稳定性.

1 半线性反应扩散模型的稳定性

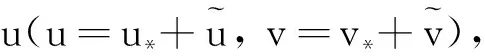
(3)

对系统(3)在(0,0)处线性化可得如下近似方程：

(4)

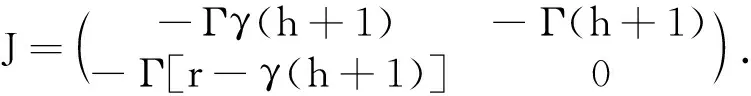
(5)

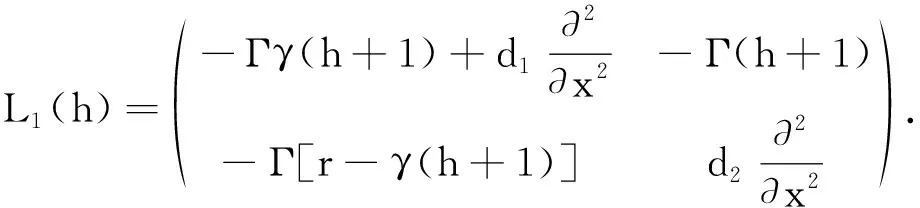
(6)

λ2-T1(k)λ+H1(k2)=0，

(7)

其中T1(k)=tr(L1k)=-Γ(h+1)-(d1+d2)k2,

H1(k2)=det(L1k)=[Γγ(h+1)+d1k2]d2k2+detJ.

(8)

定理1由于T1(k)≠0,k=0,1,2,…， 线性自扩散模型(2)不会出现Hopf分支.

定理2当r>γ(h+1)时，模型(2)的唯一正平衡点E*(u*,v*)是局部渐近稳定的.

定理3线性自扩散模型(2)不会诱导Turing不稳定性.

2 数值模拟与讨论

为验证所得定理的正确性，在模型(2)中取r=4.8,γ=1,Γ=5,h=3，d1=1,d2=4.经计算，该取值满足定理条件r>γ(h+1)， 且模型(2)存在唯一正平衡点E*(4,0.8).由定理2可知该正平衡点是局部渐近稳定的.根据上述取值绘制的食饵和捕食者的种群密度随时间和空间的变化趋势如图1和图2所示.由图1和图2也可以看出，正平衡点E*(4,0.8)是渐近稳定的.由此进一步表明，线性自扩散不会改变Lotka -Volterra捕食者-食饵模型的稳定性.

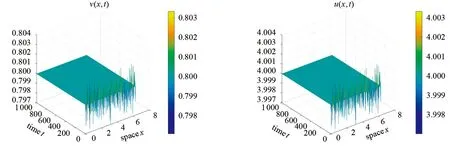
图1 食饵种群密度随时间和空间的变化趋势 图2 捕食者种群密度随时间和空间的变化趋势