一类含不定非线性项椭圆方程的正解

林美琳

(应用数学福建省高校重点实验室(莆田学院)， 福建 莆田 351100)

0 引言

本文考虑如下一类带权的含有不定非线性项椭圆方程正解的存在性问题：

(1)

由于本文采用变分方法来求解方程的解，因此首先给出下列Euler -Lagrange泛函：

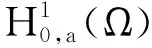
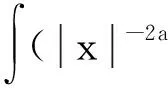
成立.于是再由椭圆正则性估计可知，u∈C2(Ω{0}).

定理1若条件(A)成立，且μ∈(0,μ1)， 0≤λ<Λ-(1+a)2， 则方程(1)至少存在1个正解.

1 预备知识

本文考虑如下极小问题：

由于S0是Sobolev嵌入的最佳常数，因此由文献[5-8]可知S(a,b,μ)的一组达到函数为：

(2)

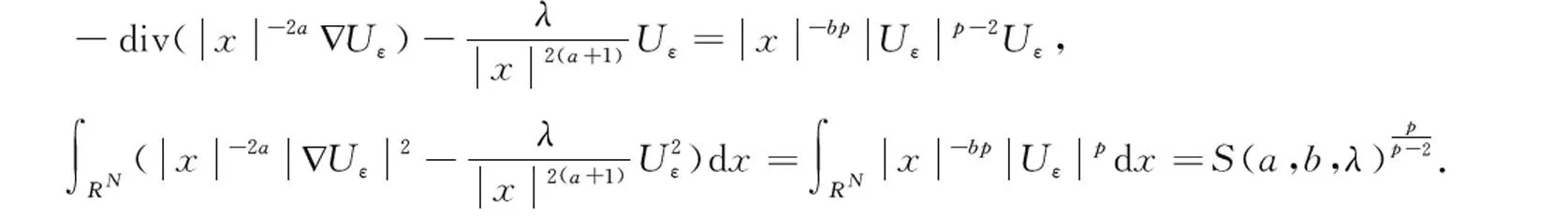
(3)

(4)

(5)

(6)

2 相关引理及其证明

考虑如下Nehari流形：

Mμ={u∈Ha;G(u)=〈J′μ(u),u〉=0,u≠0}.

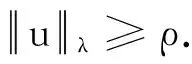
证明对于∀u∈Mμ，由条件(A)和Sobolev不等式可得：

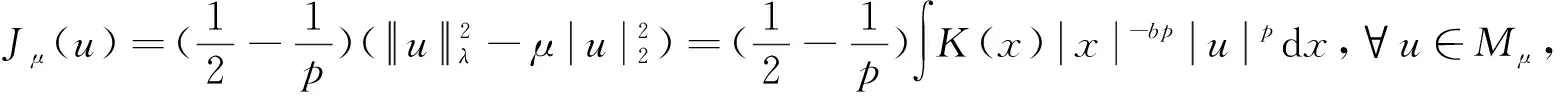
证明因{un}⊂Mμ, 0<μ<μ1, 所以有：

由上式可知{un}在Ha中有界.于是可以选取一个子序列{un}， 在Ha中un⇀u(n→∞)， 在Ω中un→u, a.e.(n→∞).由集中紧性原理[10]可知，在Ω中存在至多可数集I, 使得：

(7)

(8)

(9)

(10)

Λγ0≤α0.

(11)

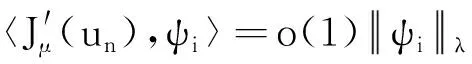
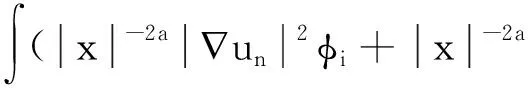
令n→ +∞， 由此可得αi≤K(xi)βi≤|K|∞βi.再由式(9)可得βi=0或βi≥(S0/|K|∞)p/(p -2).下证βi=0.若存在i∈I, 使得βi≠0， 则由测度β的有界性可知，集I有限.由此再利用Brezis -Lieb引理[11]可得：

显然知上述不等式矛盾，因此对任意的i∈I, 有βi=0.

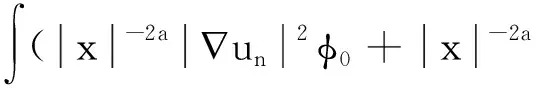
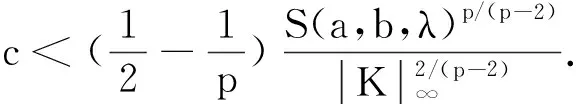
证明取t0vε∈Mμ(vε的定义见本文中预备知识)，于是由计算可知

再根据式(3)—式(6)可得：

定理1的证明由引理2— 引理5可知，c是可达到的.设ω∈Mμ达到c.由于{un}是Jμ(u)在Mμ上的极小化序列，因此{|un|}也是.另外，由引理2—引理5还可知，可设ω为Jμ的一个非负临界点，即ω为方程(1)的一个非负解.于是由强极值原理可知ω为方程(1)的一个正解，证毕.