广义三阶非线性薛定谔方程的行波解

叶飞筠， 刘小华， 曾职云

(贵州民族大学 数据科学与信息工程学院， 贵阳 550025)

0 引言

非线性薛定谔方程(NLSE)在物理学、生物学等领域具有重要作用[1-2].为了构造NLSE的各种形式的行波解，学者们提出了许多有效的方法，如F-展开法[3]、雅可比椭圆函数法[4]、扩展的辅助方程法[5]、G′/G展开法[6]、 Riccati展开法[7]、正弦余弦法[8]等.本文将利用双曲正切函数展开法研究如下广义三阶非线性薛定谔方程[9]

i (qt+qxxx)+|q|2(δ1q+iδ2qx)+iδ3(|q|2)xq=0

(1)

1 改进的双曲正切函数法

首先考虑如下非线性偏微分方程：

N(q,qx,qt,qxx,…)=0.

(2)

为了构造方程(2)的精确行波解，本文引入如下行波变换：

q(x,t)=φ(ξ),ξ=ax+ct,a,c≠0,

(3)

其中a、c分别表示频率和波数.将式(3)代入式(2)可将式(2)化为如下常微分方程：

N(q(ξ),aq′(ξ),cq′(ξ),a2q′(ξ),…)=0.

(4)

假设式(4)具有如下形式的解：

(5)

且α满足

α′=b+α2.

(6)

其中b是待确定的参数，A0、Aj、Bj(j=1,2,…,n)是任意常数，α=α(ξ)，n由齐次平衡原则确定.将式(5)和式(6)代入式(4)后合并αj(j=0,1,2,…,n)的同次幂，并令同次幂的系数为零，由此可得到关于A0、Aj、Bj(j=1,2,…,n)、b、a和c的代数方程组.求解该代数方程组后再结合方程(6)的几种情况的解[16](式7—式11)，即可给出方程(2)的有界行波解的精确表达式.

1) 当b<0时，方程(6)有如下双曲函数解：

(7)

(8)

2) 当b=0时，方程(6)有如下有理函数解：

(9)

3) 当b>0时，方程(6)有如下三角函数解：

(10)

(11)

2 精确行波解

本文基于上述改进的双曲正切函数展开法构造方程(1)的有界行波解的精确表达式.首先引入如下行波变换：

q(x,t)=φ(ξ)ei η(x,t)，ξ=kx+ωt，η(x,t)=δx+λt,

(12)

其中k和δ为孤子的频率，ω和λ为波数.将式(12)代入式(1)，并分别令实部和虚部为零可得：

3δk2φ″+(λ-δ3)φ+(δ2δ-δ1)φ3=0，

(13)

k3φ‴+(ω-3kδ2)φ′+k(δ2+2δ3)φ2φ′=0.

(14)

对式(14)关于ξ进行积分，并令积分常数为0， 则有：

(15)

φ(ξ)=A0+A1α+B1α-1.

(16)

将式(16)及φ的二阶导数代入式(15)后合并α±j(j=0,1,2,3)的同类项系数，并令其为0可得到如下关于A0、A1、B1和ω的代数方程组：

(17)

求解方程(17)可得ω、A0、A1、B1的值有以下几种情况：

(18)

(19)

(20)

(21)

(22)

(23)

由式(18)、(19)以及式(7)—(12)可得方程(1)有如下的有界行波解：

1) 当b<0时，方程(1)有如下的双曲函数解：

(24)

2)当b=0时，方程(1)有如下的有理函数解：

(25)

3)当b>0时，方程(1)有如下的三角函数解：

(26)

由式(20)、(21)以及式(7)—(12)可得方程(1)有如下的有界行波解：

1) 当b<0时，方程(1)有如下的双曲函数解：

(27)

2) 当b=0时，方程(1)有如下的有理函数解：

(28)

3)当b>0时，方程(1)有如下的三角函数解：

(29)

由式(22)、(23)以及式(7)—(12)可得方程(1)有如下的有界行波解：

1) 当b<0时，方程(1)有如下的双曲函数解：

(30)

2) 当b=0时，方程(1)有如下的有理函数解：

(31)

3) 当b>0时，方程(1)有如下的三角函数解：

(32)

3 解的性态分析

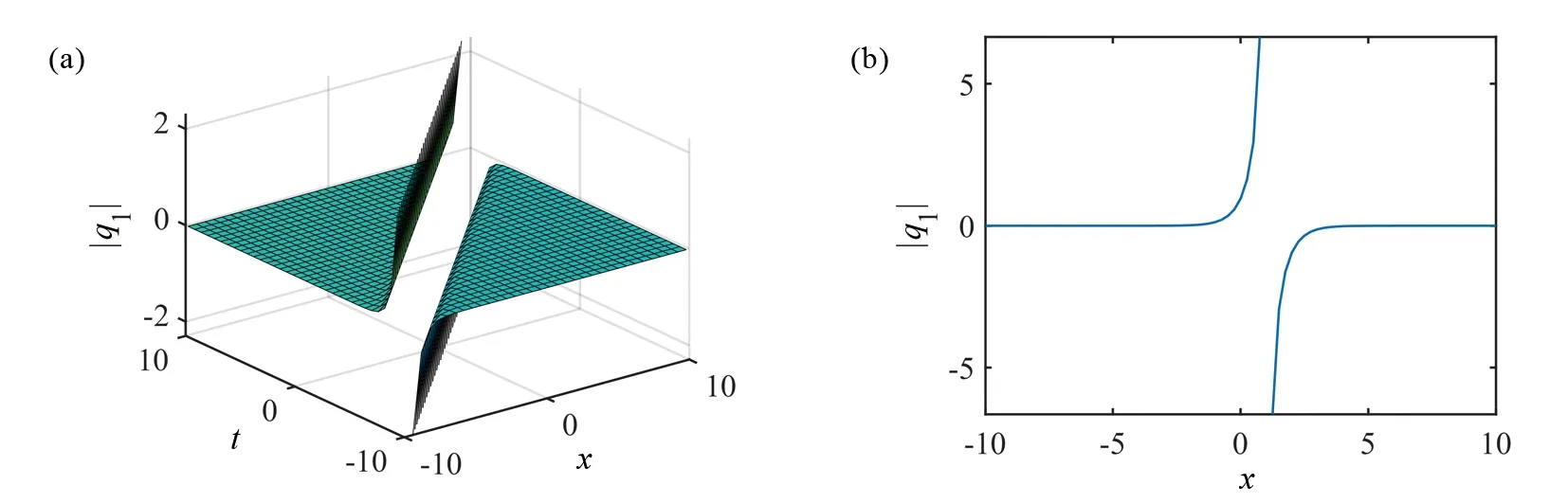
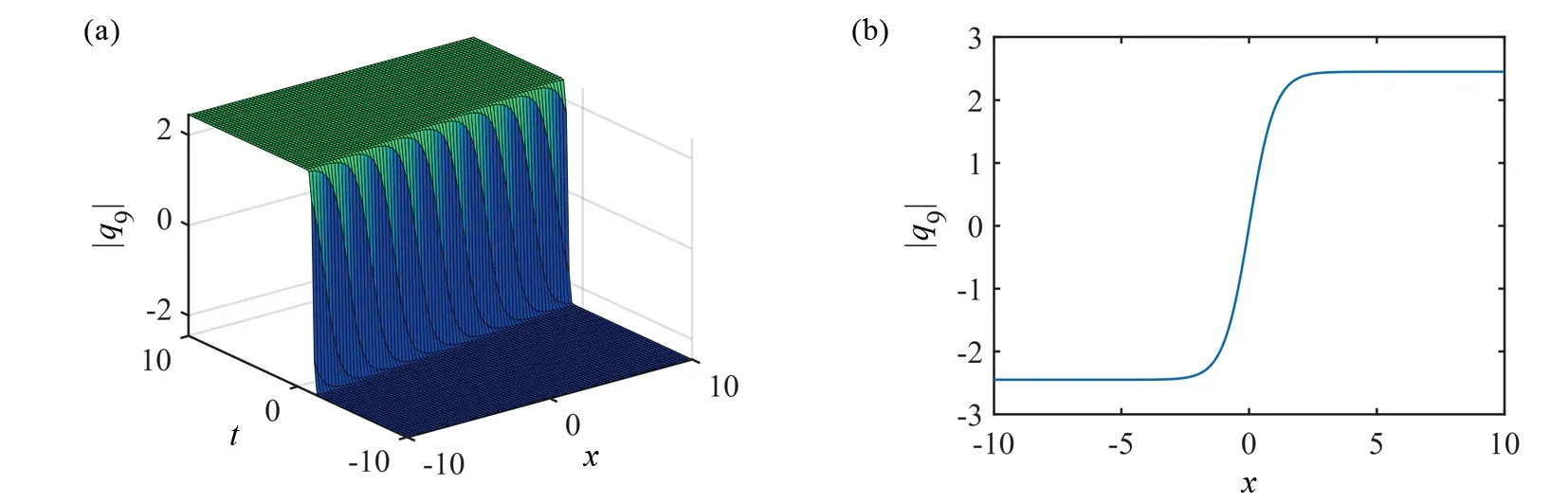
图1是方程(1)的解|q1|在-10

图1 解|q1|的3D图(a)和2D图(b)

图2 解|q3|的3D图(a)和2D图(b)

图3 解|q7|的3D图(a)和2D图(b)

图4 解|q9|的3D图(a)和2D图(b)