一种广义扩展型増广拉格朗日方法

于奥林， 孔玉倩， 申远

(1.南京财经大学 红山学院， 南京 210023； 2.南京财经大学 应用数学学院， 南京 210023)

0 引言

増广拉格朗日方法(ALM)是求解线性约束凸优化问题的经典算法.线性等式约束的凸优化模型为：

min{θ(x)|Ax=b,x∈χ},

(1)

其中θ(x):Rn→R是一个闭凸函数(不一定是强凸或光滑的),χ⊆Rn是一个闭凸集,A∈Rm ×n,b∈Rm.由于x的子问题不易求解，因此通常将问题(1)迭代为：

(2)

其中：β>0是罚参数，λ∈Rm是拉格朗日乘子，x和λ分别为原始变量和对偶变量.

优化问题(1)的拉格朗日方程为L(x,λ)=θ(x)-λT(Ax-b), 其中(x,λ)∈χ×Rm.令拉格朗日方程的鞍点为(x*,λ*)， 则有：

Lλ∈Rm(x*,λ)≤L(x*,λ*)≤Lx∈χ(x,λ*).

上式等价于以下变分不等式：

(3)

式(3)的紧凑形式为如下单调变分不等式(VI):

ω*∈Ω,θ(x)-θ(x*)+(ω-ω*)TF(ω*)≥0,∀u∈Ω,

(4)

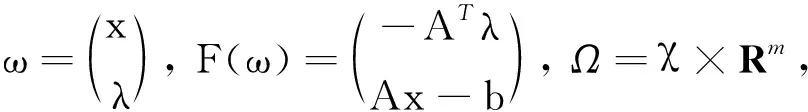
(5)

(6)

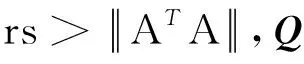
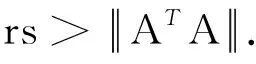
(7)

由文献[1]可知，式(7)是对偶 -原始迭代顺序的定制邻近点算法(C -PPA)[1].为了更好地求解优化问题(1)，文献[2]的作者在平衡増广拉格朗日方法(B -ALM)的基础上增加了Ax≥b这一条件，进而可较为容易地计算出经典ALM(2)中的两个子问题.

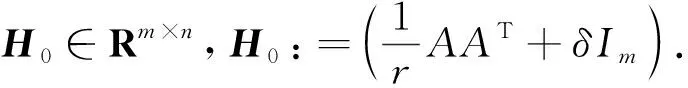
(8)

(9)

1 广义扩展型增广拉格朗日算法

本文考虑更一般的凸规划模型，该模型包括线性不等式约束和不等式约束：

min{θ(x)|Ax=b(或≥b),x∈χ}.

(10)

GEALM算法s(s>0)、γ(γ>0)、β(β>0)和r(r>0)是任意常数， (xk,λk)为给定的迭代点，新的迭代点(xk +1,λk +1)由以下步骤产生：

(11)

GEALM算法的收敛性取决于以下矩阵的正定性：

(12)

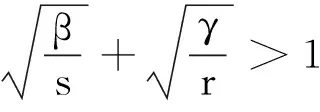
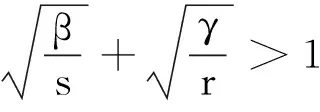
引理2GEALM算法产生的序列{ωk=(xk,λk)}可使下式成立：

ωk +1∈Ω,θ(x)-θ(xk +1)+(ω-ωk +1)TF(ωk +1)≥(ω-ωk +1)TH(ωk-ωk +1),∀ω∈Ω.

(13)

证明在式(11)中，关于x的子问题的解可描述为：

在上式中，对于任何未知的λk +1均有：

xk +1∈χ,θ(x)-θ(xk +1)+(x-xk +1)T(-ATλk +1)≥

(14)

同理，式(14)中关于λk +1的子问题的解可由下式描述：

由以上可得：

λk +1∈Λ, (λ-λk +1)T(Axk +1-b)≥

(15)

联立式(14)和式(15)，由此再根据式(4)中的符号即可得式(13).证毕.

引理3GEALM算法产生的序列{ωk=(xk,λk)}可使下式成立：

θ(x)-θ(xk +1)+(ω-ωk +1)TF(ω)≥

(16)

证明由于式(4)定义的算子F是带有斜对称矩阵的仿射算子，因此有：

(17)

由式(17)可知(ω-ωk +1)TF(ωk +1)=(ω-ωk +1)TF(ω)， 由此进一步可知式(13)的左端等价于θ(x)-θ(xk +1)+(ω-ωk +1)TF(ω).综合上述可知：

ωk +1∈Ω,θ(x)-θ(xk +1)+(ω-ωk +1)TF(ω)≥(ω-ωk +1)TH(ωk-ωk +1),∀ω∈Ω.

(18)

(19)

将式(19)代入式(18)的不等号右边即可得证引理3.

定理1因在GEALM算法生成的序列{ωk=(xk,λk)}中含有矩阵H， 且在式(12)中定义了该矩阵，因此序列{ωk}满足：

(20)

证明将式(16)中的ω设为任意固定的ω*∈Ω*， 则由此可得：

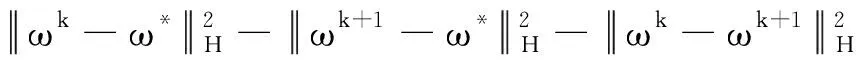
2{θ(xk +1)-θ(x*)+(ωk +1-ω*)TF(ω*)},∀ω*∈Ω*.

由于ω*∈Ω*，ωk +1∈Ω， 所以根据式(4)可知上述不等式的不等号右端为非负，定理1得证.

定理2因在GEALM算法生成的序列{ωk=(xk,λk)}中含有矩阵H， 且在式(12)中定义了该矩阵，因此序列{ωk}可收敛到某个ω∞∈Ω*.

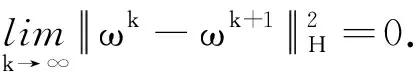
ωkj∈Ω,θ(x)-θ(xkj)+(ω-ωkj)TF(ωkj)≥(ω-ωkj)TH(ωkj-1-ωkj),∀ω∈Ω.

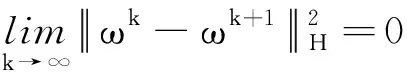
ω∞∈Ω,θ(x)-θ(x∞)+(ω-ω∞)TF(ω∞)≥0,∀ω∈Ω.

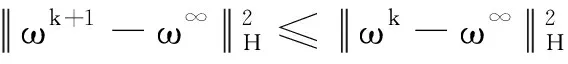
2 数值实验

实验环境为：笔记本电脑，处理器为Intel Core i5 -8250U CPU@1.60 GHz 1.80 GHz，内存为4 GB，系统为Windows10，软件为MATLAB R2016b.实验中给定矩阵C为对称矩阵.在F-模下求与C距离最近的相关性矩阵为：

(21)

由表1和表2及图1—图4可知，在矩阵取不同维度和tol取不同数值时， GEALM算法在迭代次数、CPU运行时间、收敛速度等方面显著优于C -PPA算法，由此表明GEALM算法优于C -PPA算法.

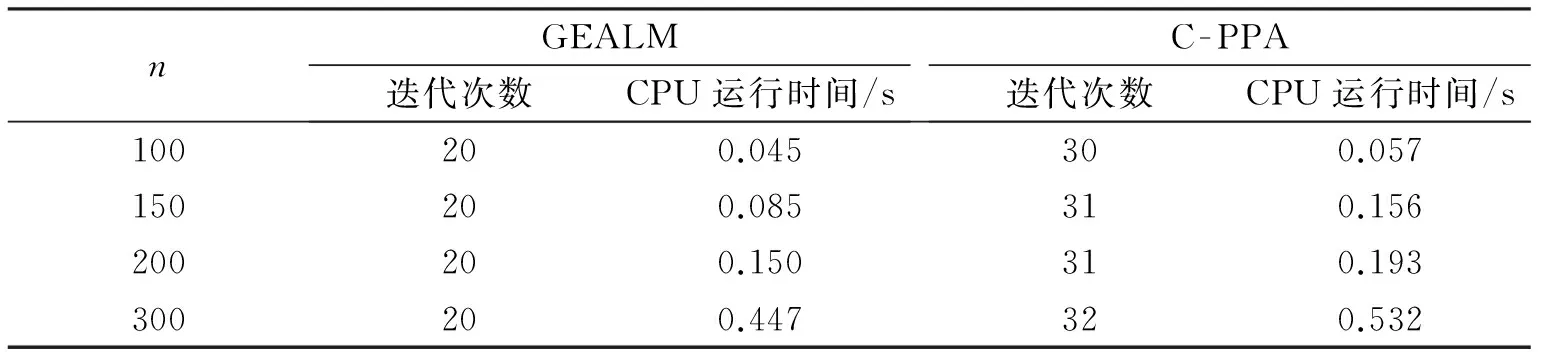
表1 tol=le-10时2种算法的迭代次数和CPU运行时间

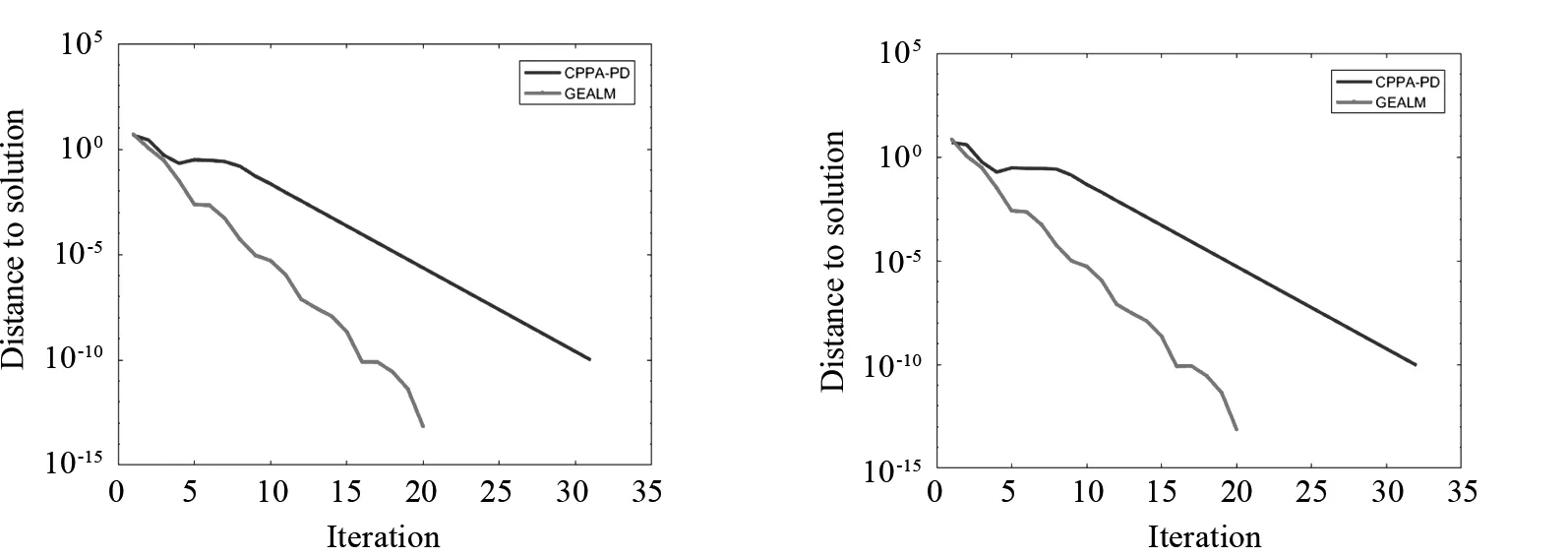
图1 n=150时2种算法的迭代变化 图2 n=300时2种算法的迭代变化

表2 tol=le-12时2种算法的迭代次数和CPU运行时间

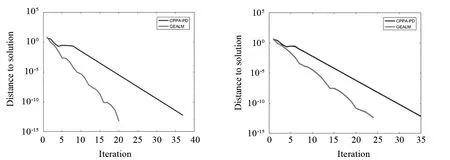
图3 n=100时2种算法的迭代变化 图4 n=200时2种算法的迭代变化