图切割快速生成扇区的蚁群算法

叶志坚，王建忠，张召悦，杨群亭，牟龙芳

中国民航大学 空中交通管理学院，天津 300300

管制扇区是指一块划定高度和水平范围的管制空域。早期飞行活动主要在终端空域，划分的扇区形状接近扇形，而随着交通越来越复杂，为降低管制员的工作负荷，航路空域也需要划分成更多的扇区，但是航路扇区形状大都不是扇形。扇区大小是根据交通流量、三维空间范围和管制员的工作量来确定的。划分扇区的目的是为了管制员在能力范围内公平组织交通并保持航空器安全间隔，从而实现管制空域安全、高效和快速地运行。

需求与容量的管理一直是交通运输领域的核心研究领域。一般来说，容量和基础设施有密切关系，容量的提升需要较长的时间和巨大的投入。当天气等因素造成容量下降或者预测的需求会超过容量时，通常的做法是控制需求；但随着航空领域研究和实践的发展，欧美等国的研究人员提出了通过动态改变管制员管辖范围来提升空域通行能力的思路并付诸实施，这种做法称为动态空域管理[1]。这与国内的开扇、合扇类似，但更加动态，更加强调空域划分扇区适应交通需求，控制需求被视为需求与容量管理的次优方案[2]。研究和推广动态扇区划分运行范式，对改善民航空管运行效率以满足我国巨大的航空交通需求具有重要意义。

动态空域划分研究的第一个热点是管制员工作负荷或者说是空域的复杂度，管制员工作负荷是管制员主观感受到的负荷，而空域复杂度是造成管制负荷的根本原因。通过回归分析法或采用机器学习可以找到两者之间的相关性联系[3]。通过对操作者在工作中的表现[4~6]或借助眼动仪[7]等测试设备，建立任务负荷关联模型来测试管制员工作负荷，也得到了国内学者的广泛研究。但到目前为止，无论是复杂度模型还是管制员工作负荷模型都没有统一标准。目前欧美采用的容量标准就是最简单的航空器数量[8]。这正如奥卡姆剃刀理论在很多领域的运用一样，如果你有两个或多个原理，它们都能解释观测到的事实，那么你应该使用简单或可证伪的那个，直到发现更多的证据[9]。另外，简单有效的模型能减少扇区负荷的计算时间。

动态空域划分研究另一个研究热点是扇区划分的模型和算法。由于动态扇区划分核心就是要及时调整空域结构适应交通和环境的变化，因此算法的计算时间决定了模型能否用于实际运行。第一种是基于图的模型，图由边和顶点构成，边表示航段，其顶点表示现有航路的交点[10-12]。第二种是基于单元空域增长的模型。首先，将空域划分为比所研究扇区更小的单元空域块，然后对单元空域块进行重组得到扇区。单元空域块有采用正方形的，根据网络流计算每个正方形空域块的负荷，然后再重组[13]；也有用正六边形作为单元空域块的，每个空域块的负荷包括协调负荷、监控负荷、冲突负荷和高度改变工作负荷，单元空域块的重组采用的是聚类算法，这种方法被用于TAAM（total airspace&airport modeller）系统[14]；有的单元空域块是不规则图形，采用混合整数规划算法重组单元空域块[15]，有的采用动态规划算法重组单元空域块[16-17]，有的采用遗传算法的[18]、采用背包算法[19]以及人工神经网络算法的[20]。但这两种方法都或多或少需要后处理以使得扇区形状满足特定要求[21]。第三种方法是利用Voronoi图从上到下分割空域。该方法无需后处理，可一次成型，而且能充分保证最终扇区的连通性、凸性和压缩性。这些特点使得这种方法特别有吸引力[22-25]。但这种方法需要的计算量大，计算效率不高是阻碍其有效使用的瓶颈。上述文献中只有参考文献[22]报道了计算时间，采用双层规划计算美国沃思堡中心生成16个扇区大约需要20 min时间。如果用在较为动态的环境中，该计算时间还是偏长。本文主要通过模型改进和算法改进来缩短这种自顶向下方法的计算时间。

扇区划分涉及的问题非常复杂，有动态交通流多时段的，也有静态交通流单时段的，还可以分为平面2维的，也有3维的。为了减少问题的复杂性，本文研究的是基于某个时段的历史数据，推演今天同一时段的优化扇区结构，是一个静态2维的扇区划分方法，本文的工作主要聚焦在2维模型的求解上。为未来的研究中结合交通流预测，采用计算机扇区自动动态辅助设计奠定基础。

本文主要创新工作主要体现在以下几点：采用航空器在所研究时空范围内4D（4Dimensional）轨迹态势判断为基础来计算工作负荷，大大缩短了计算工作负荷时间；采用自顶向下切割空域方法，一次成型，减少了预处理时间；通过动态步长结合蚁群搜索算法自身具有的个体和群体信息交互能力和并行性，生成满足约束条件的可行解，提高了计算过程的收验速度。这些工作为快速产生空域划设预案，减少计算机扇区辅助设计的时间，服务动态空域运行模式，提升管制席位适应动态变化的交通流奠定了基础。

1 问题描述

1.1 4D轨迹态势与任务负荷的关系

为了求解飞机的四维轨迹在某个时间间隔[τi,τi+1)内穿越扇形边界的准确次数，假设航空器f进入扇区时间表达成，航空器f飞出扇区的时间是。通过以下的例子来推导航空器的协调次数和在扇区中的飞行时间。

假定太原区调空域只有一个扇区，假定在τi=9：00时，有七架飞机（AC1、AC2、AC3、AC4、AC5、AC6、AC7），它们的位置在黄色圆圈指示的位置，τi+1=9：15时，它们沿4D轨迹移动到箭头位置，如图1所示。

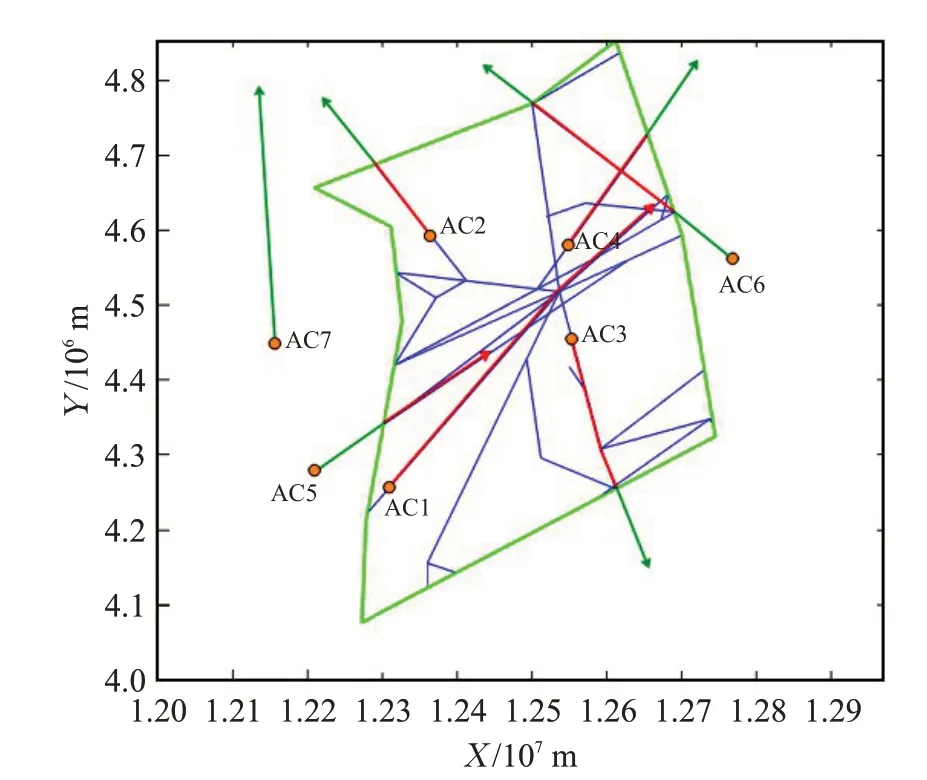
图1 7架飞机9：00—9：15的历史轨迹Fig.1 Historical tracjectory of 7 aircrafts during 9：00—9：15

在09：00—09：15间隔时间内，由一架飞机引起的监测负荷仅与该飞机在太原空域内（红色部分）4D轨迹的飞行时间有关，由一架飞机引起的协调负荷与飞机穿越边界的次数有关。有以下几种情况。

情况1 AC2、AC3和AC4在间隔[τi,τi+1)开始时，τi=9：00，飞机已经在扇区内，，在间隔结束时，飞机在扇区外，。而且所以当进出扇区时间和时间段有以下关系时：，则每个航空器与空中交通管制协调一次，在时间段[τi,τi+1)内航空器在扇区内的飞行持续时间为

情况5在属于在时间段[τi,τi+1)内未曾经过扇区，前面4种情况都是在时间段[τi,τi+1)内经过扇区的。因此，只要判断飞机轨迹在时间段[τi,τi+1)内的是否经过扇区，可以判断飞机是否进入扇区，进入扇区的航空器分以下4种情况计算协调次数和持续飞行时间，如表1。

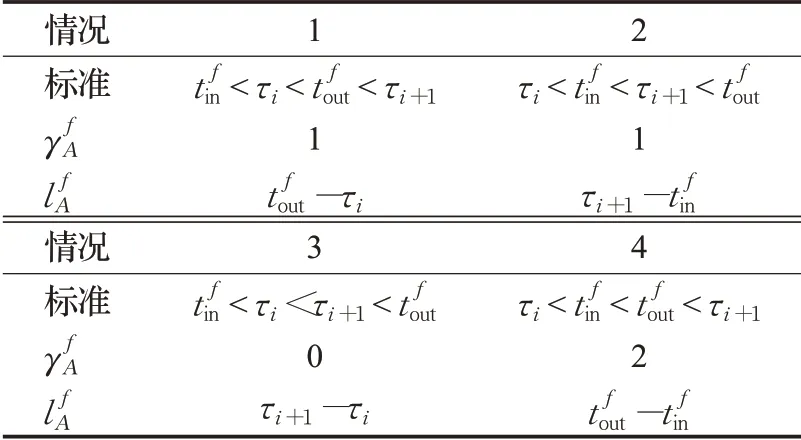
表1 情况判断标准、协调次数和持续飞行时间Table 1 Situation judgment criteria，coordination times and duration of flight

1.2 任务负荷测量

将任务负荷分为监视和协调两种负荷，监视负荷包括了冲突负荷等其他类型负荷，而且和航空器在扇区内的飞行时间成正比，而协调负荷取决于协调一次的时间和协调次数。每架次航空器在扇区内飞行10 min（600 s）需要的监控时间和协调一次所用的时间，都是根据在太原区调空域现场测试统计的平均数。以下描述如何根据这两个参数，以及1.1节描述的在所研究的时空范围内航空器4D航迹的态势，来计算管制员的任务负荷。

不失一般性，假设空域A包含k个扇区，s j,j∈{1 ,2,…,k}，这些扇区预计在时间间隔[τi,τi+1）期间开放。

扇区s j的任务负荷wl s j包括监控和协调任务负荷，如下式所示：

1.2.1 监控任务负荷测量

假设有m架次飞机通过扇区s j，在间隔[τi,τi+1)内扇区s j的监视任务负荷计算如下：

ls f j是表1计算的飞机f通过扇区s j的持续时间（单位：s）。αmot是通过现场测试统计的，每架次航空器在扇区内飞行10 min（600 s）需要的监控时间。

1.2.2 协调任务负荷测量

协调任务负荷计算公式如下：

γsfj是根据表1计算的飞机f在间隔[τi,τi+1)内与s j协扇区管制员协调的次数。αcod是管制员与飞机协调一次所用的时间（单位：s）。

1.3 目标函数

有两个目标函数被用于评估解决方案。第一个目标函数是首要目标，第二个是次要目标。

1.3.1 第一个目标函数

最小化任务负荷不平衡：

使用以下公式计算任务负荷不平衡程度：

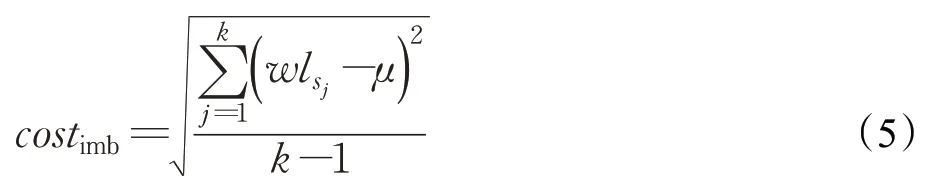
其中，k为需要开的扇区数；j为扇区标号；μ为平均任务负荷为扇区s j中的总任务负荷。扇区s j的总任务负荷包括监视负荷wlmons j和协调负荷wlcods j。

1.3.2 第二个目标函数

最小化总协调任务负荷：

协调任务负荷是影响任务总负荷的关键因素。由于假设监测工作量与飞行器在空域的飞行时间成正比，因此几乎不可能降低总的监测任务负荷。因此，一个好的空域配置方案必须是最小协调任务负荷的方案。一种扇区划分方案的总的协调负荷是公式（3）表示的各个扇区协调负荷的累计。但不能忽略监视负荷，因为监视负荷涉及到工作负荷平衡，这体现在第一个目标函数中。总的监视任务负荷的计算公式如下：

1.4 约束条件

考虑了三个约束条件。首先，每个扇区的平均停留时间必须大于一定阈值。其次，必须限制每个扇区的总负荷量，不能太大，也不能太小。最后，从扇区边界到任何关键交叉点的距离必须满足最小距离约束。

1.4.1 平均停留时间约束

美国联邦航空局的扇区容量计算是基于监控警报参数（monitor alert parameter，MAP）计算的[26]。MAP大约是扇区平均驻留时间（average dwell time，ADT，单位：min）的5/3。这意味着更大的平均驻留时间将有助于提高扇区容量。平均驻留时间测量如下：

各扇区的平均驻留时间的约束可以表示为：

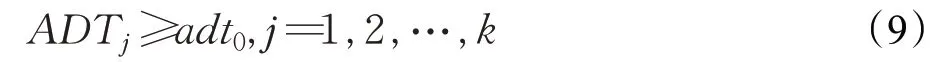
adt0是用户定义的平均驻留时间的最小允许值。为了保证能计算每架次航空器的平均驻留时间，将数据提取时间由[τi,τi+1)扩展到[τi-1,τi+2)，保证在时间段[τi,τi+1)空域中出现的飞机，在时间段[τi-1,τi+2)都能完成穿越扇区。

1.4.2 任务负荷约束

理论上，管制员可以有效使用的最大可接受任务负荷(wlmax)必须小于可用时间。假设在计划期间[τi,τi+1)，每个管制员的工作负荷的上限是：

为了公平起见，管制员在各扇区的负荷不应低于平均负荷μ太多。因此，每个扇区的工作负荷约束如下所示：

α1和α2是用户定义的介于0和1之间的值，大多介于0.6和0.9之间。μ是平均工作负荷，每个管制员的负荷可以在平均工作负荷附近波动，但是必须小于α1(τi+1-τi)，(τi+1-τi)是工作周期，是一个时间段，总的用时间表示的工作负荷不能大于α1(τi+1-τi)。实际应用场景中会有高工作负荷（大交通流）情况或者低工作负荷情况，低交通流强度情况下，管制员一般不会超负荷，α1和α2可以设置比较小的值，而高强度交通流情况下，α2尽量接近1比较好，α1的设置要根据实际管制员的水平尽量大一些，强度越大，需要大家共同分担的任务越多。

1.4.3 最小距离约束

扇区边界和任何关键交叉点之间的距离不得小于给定距离。此约束确保管制员有足够的时间解决此节点上可能发生的冲突。将由至少两条路线的交叉口形成的交叉点，且交通流量达到2架次/15 min的定义为临界交叉口。如果至少存在Q个临界交点，则从每个临界交点到任何一个扇区边界（多边形）的水平距离不能小于用户定义的距离D0。

从临界交叉点p i:(φi,λi)到任何扇区s j的边界的水平距离可以表示为如下：

使用文献[27]中的方法来求解这个距离。那么，最小距离约束可以表示为：

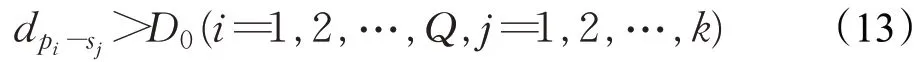
2 切割空域的蚁群智能算法

如前所述，为了充分利用Voronoi图能满足凸性、连通性和压缩性的特点，来切割空域成扇区，前面描述了具体的问题和模型，这一章主要研究如何采用蚁群智能算法实现问题的求解。

国外采用Voronoi图切割空域的文献中的模型求解基本都用遗传算法[22-25]，而且计算时间偏长；国内有文献采用了蚁群算法求解，但从最终解的图形结果来看，是多个Voronoi图组合成扇区，并没有实现利用Voronoi图直接切割成具有Voronoi图显著特征的完整扇区，理论上还是属于元素扇区重组的范畴[28-30]。本章主要描述解的表达形式和采用蚁群算法的求解过程。

2.1 解的表达形式

用Voronoi图切割空域，有一个显著的特点：在空域边界确定的情况下，最终扇区的形成主要取决于Voronoi图的产生点的位置，即Voronoi图的产生点和最终解有一一对应关系。因此，假设要划分成k个扇区解的表达式可以写成如表2形式。

表2 解的表达形式Table 2 Expression of solution

2.2 蚁群算法的解与蚁群个体的信息映射

为了理解中间解和最终解的关系，以及解与蚁群个体间的关系，下面以父体产生初始种群为例来做说明。不失一般性，假设空域要划分成k个扇区，蚁群算法的种群数量为g。种群的产生过程，解及其个体信息的映射关系如下：

（1）将空域边界顶点的坐标转换为平面坐标。

（2）如图2所示，在所研究空域生成均衡分布的点。

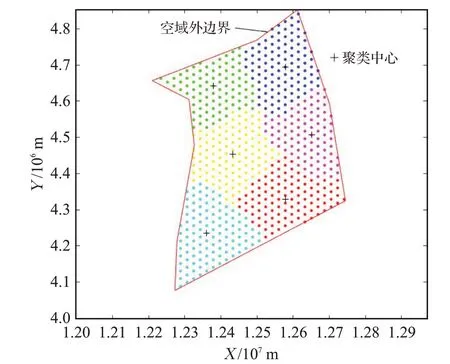
图2 均衡分布的点及聚类中心Fig.2 Evenly distributed points and clustering centers

（3）在第一代扇区生成之前，将上一步生成的这些点的K均值聚类中心（图2中“+”号显示位置）作为Voronoi图的生成点。算法开始只有一个父代，尚未产生种群，需要在其周围邻域范围内构造种群，种群中的个体至少有一部分足所在位置一定和聚类中心位置不同。如果种群数量为g，生成k个扇区，则一个蚂蚁个体有k个足，而且为了保证多样性g只蚂蚁的足应该不完全相同。为了让个体有差异，需要用图4所示的聚类中心（圆圈中心）周围圆圈上的点（聚类中心的邻域）来替换聚类中心，生成其他个体。聚类中心作为父体，生成种群个体时，为了保证个体的多样性，需要位置替换；在每次个体更新的时候也要替换，每次替换，相当于个体的位移（传统蚁群算法，是蚂蚁只有一个位置，本文的个体有k个足，k个位置（在2维平面上），相当于k×2维下的一个位置）。个体只有发生位移才能去探索寻优。位置替换以后，个体就可以在寻优过程中交换信息，提高并行性能。如果仅仅一个聚类中心，相当于种群只有一个个体。

（4）使用上一步获得的某个个体的生成点（k只足），即表2所述的中间解，产生扇区，即表2所述最终解（由每个扇区边界顶点构成），例如，如图3所示，扇区是利用上一步获得的Voronoi图生成点生成的Voronoi图切割所研究空域产生的。图3只是一个个体切割空域的例子，种群数量有g个个体，则有这样的空域切割方案g个。

图3 按生成点生成扇区示意图Fig.3 Generating sectors schematic by generating points

（5）在图3的基础上就可以计算某个个体对应的信息：每个扇区的工作负荷、个体中最小工作负荷、个体中最大工作负荷、个体中平均工作负荷、不平衡性；航空器平均驻留时间，扇区边界到重要点的距离。

解对应的映射信息，是蚁群个体间传递信息的基础，也是解是否可行判断以及优选的基础。

2.3 蚁群算法的中间解产生机制

不失一般性，假定蚁群个体数量是g个，ps代表个体上标，则，代表一个中间解。如图4所示，空域要分成k=6个扇区，6个扇区的初始中间解位置在6个Voronoi图中的圆圈中心位置。

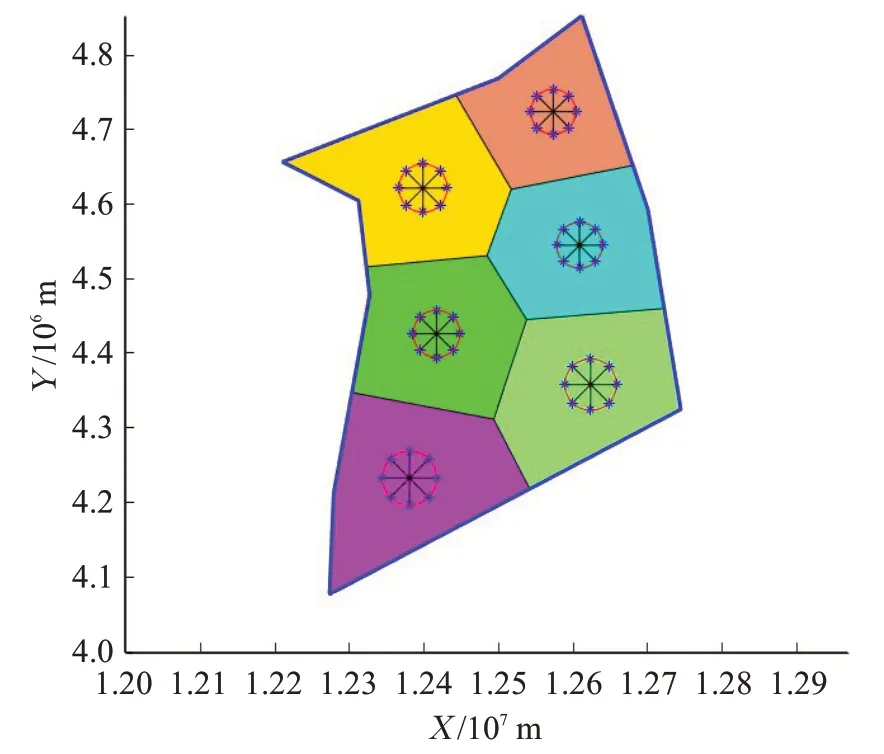
图4 当前生成点的位置和下一代备用生成点的位置Fig.4 Location of current generation point and next generation standby generation point

定义个体最优解为个体在历代寻优过程中的最优值，表达式如下：

等式（23）和（24）中的参数δnc-1被用于限制位置调整量。如果一个扇区的工作负荷接近个体的平均工作量，则调整幅度会更小。否则，将进行更多的调整。算法初期，扇区可能不平衡性比较大，在当前位置附近可能没有接近平衡的点集存在，位置调整量就大些，以便搜索到更平衡的解；在已经接近平衡的情况下，最优解可能就在附近，需要减少移动步长，增加搜索精度。该参数计算公式如下：

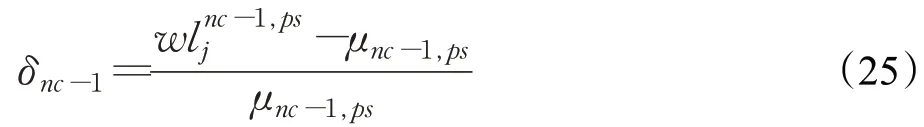
等式（23）和（24）中的还有三个步长调整参数，在参考文献[31]中步长都是固定的（γ1=0.7，γ2和γ3都是1.4）。调整这三个参数，使它们随着迭代次数的增加而减少，如图5所示。

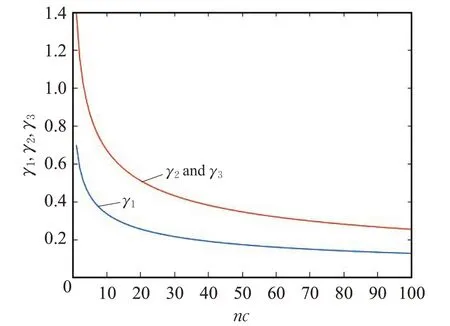
图5 γ1、γ2和γ3随着迭代次数的变化Fig.5 γ1，γ2 and γ3 changing with number of iterations

三个参数（γ1，γ2，γ3）随着迭代次数的增加而减少可以使后期位置变化更小，扇区的负荷值变化也更小，精度更高，更容易收敛到负荷平衡点，这三个参数随着迭代次数变化的公式如等式（26）、（27）所示：

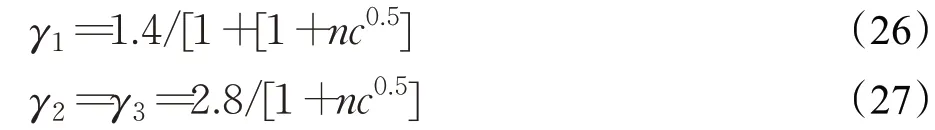
其中，nc是当前迭代次数。

2.4 满足目标的帕累托前沿选择机制和最优解产生流程

如前所述，主要目标是扇区负荷平衡，次要目标是总工作负荷。为了得到尽可能平衡的扇区结果，在优选可行解的时候，只选择扇区负荷不平衡越来越小的方案，而允许选择总工作负荷高于前一代的可行解。随着代数的增加，允许高于前一代总工作负荷的值越来越小。优选条件表达如下：

式中，F2是前一代最佳可行解的总工作负荷，F′2是当前一代某个可行解的的总工作负荷。γ1的表达式见等式（26）。在种群中个体数量为g，生成k个扇区的情况下，最优解产生流程如图6所示。

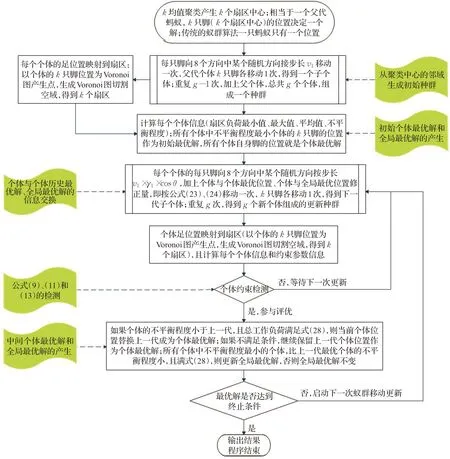
图6 蚁群算法流程图Fig.6 Flow chart of ant colony algorithm

2.5 算法终止条件根据场景设置分析

算法的解首先要满足约束，但探索过程允许不满足约束的中间解存在，满足约束的解才能去参与评优，评优考虑两个目标，一个是总工作负荷，一个是扇区间的不平衡性，两个目标都是越小越好，而缩小扇区间的不平衡性是主要目标，因此将“扇区间的不平衡性”的目标值作为终止条件。如果约束条件越多、越苛刻，比如在重要点分布比较密集的情况下，由于要求扇区边界距离重要点必须一定距离，则产生可行解就会变得困难，因此，在这种情况下，要通过Voronoi图切割空域得到负荷完全平衡的解就会变得非常困难，这时候就要放低终止条件要求，增加“扇区间的不平衡性”的目标值。

当然也可以用重复迭代多次，目标值没有改进作为条件，对于要求快速得到结果且对平衡性能满足允许误差要求的情况下，可能会消耗更多时间。因此，本文采用“扇区间的不平衡性”的预设值作为终止条件。

在其他场景下，采用扇区总工作负荷重复迭代多次无提升，或者扇区总工作负荷小于某个预设值也是可以的。但扇区划分中，总工作负荷最小化，往往扇区间负荷极度不平衡，除非交通流在时空上均匀分布。因此，很少以此为主要目标，或者在与平衡性构建线性目标函数时，其权重也会设置相对较小。

因此，算法终止条件的设置要综合实际应用场景，权衡优化目标、得到可行解的难易程度、算法效率、计算时间要求，来根据具体场景设置终止条件。

3 实例验证

3.1 实验设计

实验目的是为了验证了模型的正确性和测试算法的计算效率。实验采用的数据是文献[21]中的山西区调空域的交通流数据。第一个测试是计算质量测试：通过计算模型中的两个目标（不平衡程度和总工作负荷）来验证解决方案的质量，并与相关的工作进行了比较。第二个测试是蚁群算法与文献[21]中MC-CLFV算法重复100次情况下，用箱线图统计计算质量和计算效率。测试中为了比较计算质量和计算效率，将程序终止条件设置为第一个目标函数(costimb)达到120，同时第二个目标函数达到当前最小值。为了测试算法在扇区数量增加时的计算效率，松弛了关键点到扇区边界的平均停留时间约束和最小距离约束。这是由于用于研究的案例空域太小，目前只有四个扇区，如果保留这两个约束，就没有可行的解决方案，或者需要降低性能评估标准。表3列出了算法中使用的参数。

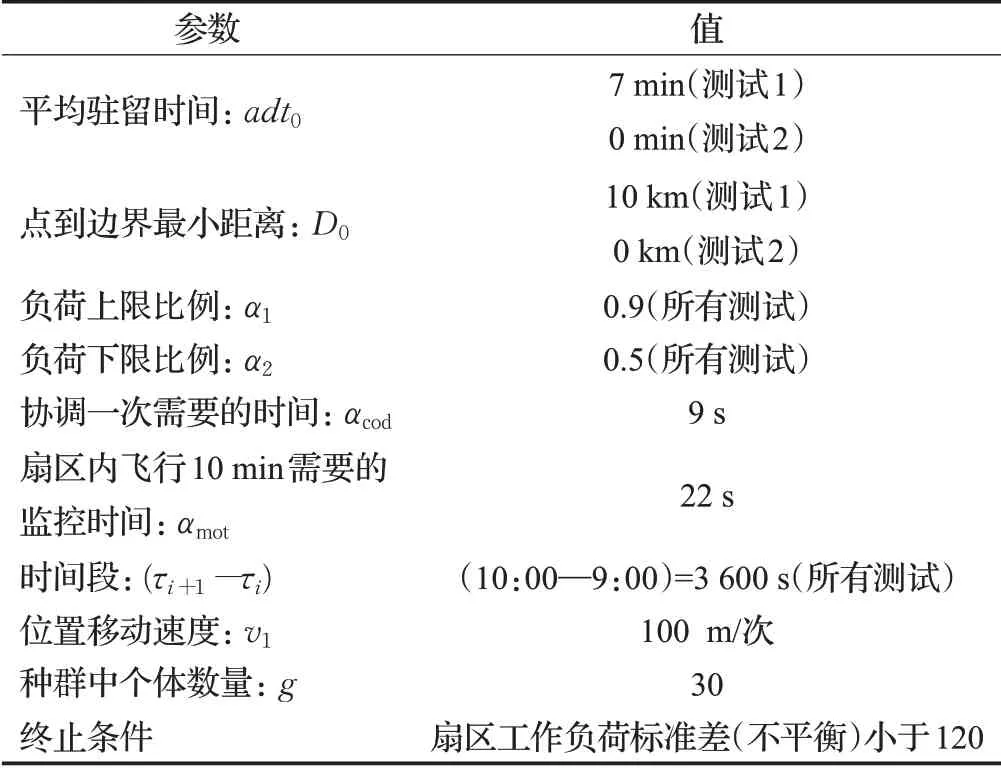
表3 算法中使用的参数Table 3 Parameters used in ant colony algorithm

在以下测试中，使用的计算机设备的处理器是英特尔®Xeon®银牌4215 CPU@2.50 GHz，使用的计算机内存是16 GB RAM。软件平台是Matlab 2018a。

3.2 测试1及结果分析

测试1在所有约束条件下，测试扇区间任务负荷的不平衡程度和所有扇区的总任务负荷，以评估解决方案的质量。两个值越低，解的质量越高。图7是由本文算法生成4个扇区的扇区结构图。

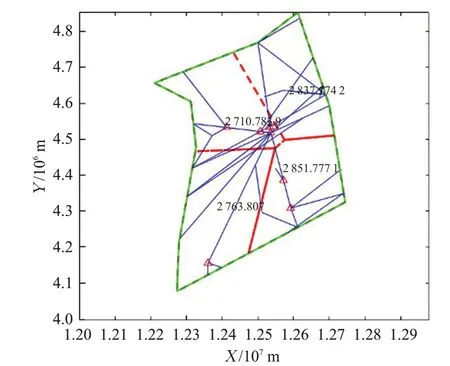
图7 蚁群算法生成的扇区Fig.7 Sectors generated by ant colony algorithm

表4 蚁群算法与以往算法结果的比较Table 4 Comparison of results between ant colony algorithm and algorithm in previous work

显然，扇区之间的平衡程度和总任务负荷，蚁群算法都优于文献[21]两种算法的结果和山西区调管制扇区当前构型下的值。

图8是3种算法随机一次生成4个扇区的不平衡性随迭代次数的变化情况对比。由于有最小距离约束，以及解的邻域不平衡目标下降，使得优化目标值不是随迭代次数连续下降，而是平台式下降，可以推断，扇区划分的解存在许多鞍点。蚁群算法具有更强的跳出鞍点的能力，MC-CLFV次之，MC-RC跳出鞍点能力最差。从图8中也可以明显观察到蚁群算法的迭代次数明显少于另外两种算法。启发式算法的结果有一定随机性，通过单次的结果比较很难有说服力，因此在测试2中做了重复100次的实验，以测试改进后的算法的性能统计优势。

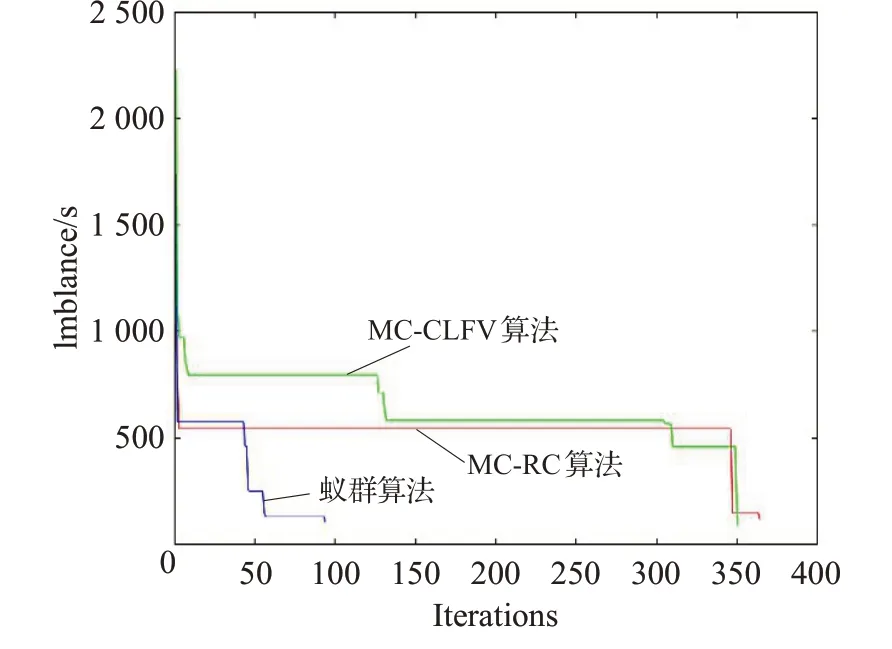
图8 不平衡性随迭代次数的变化对比Fig.8 Comparison of variation of imbalance with number of iterations

3.3 测试2及结果分析

在测试2中，测试太原空域划分为3~8个扇区时，当终止条件为δ=120时，且松弛了最小平均停留时间约束和关键点到扇区边界的最小距离约束情况下，蚁群算法和MC-CLFV算法在100次重复计算中的解质量和求解效率统计。

统计结果的箱线图如图9所示。粉色箱线图为MC-CLFV算法运行100次的任务负荷不平衡统计；蓝色箱线图为蚁群算法运行100次的任务负荷不平衡统计。在图9中的每个框上，凹陷处中心标记表示中位数值，框的底部和顶部边缘分别表示下四分位数Q1（25%）和上四分位数Q2（75%）。上下边缘用“－”表示，用“o”符号绘制异常值。

在图9中，可以看到蓝色框（蚁群算法）的中位数值、Q1和Q2小于粉色框（MC-CLFV算法）。这表明蚁群算法比MC-CLFV算法更有可能得到更好的解。同时，还观察到两种算法的三个参数随扇区数的增加而增加。这意味着，随着扇区数量的增加，解的质量都会下降。

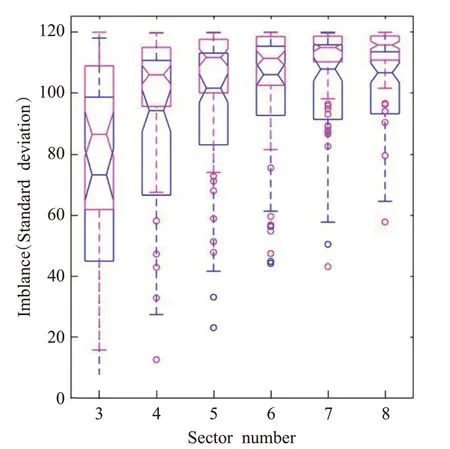
图9 两种算法不平衡性的箱线图对比Fig.9 Comparison of box line diagram with imbalance between two algorithms

两种算法的总工作负荷统计图10所示是蚁群算法（蓝色）与MC-CLFV算法（粉色）的总工作负荷比较。两种算法的总工作负荷都随扇区数量增加而增加，这是由于扇区数量增加必然增加航空器穿越扇区边界的次数，从而总工作负荷增加。两种算法都以平衡性为主要目标，因此差异不大。

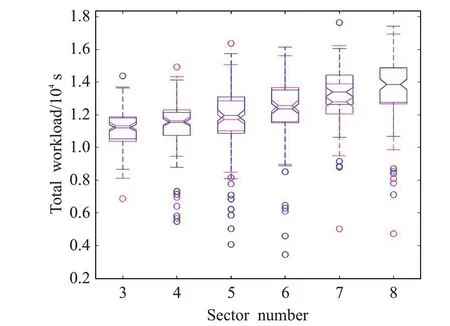
图10 两种算法的总工作负荷比较Fig.10 Comparison of total workload of two algorithms

图11是蚁群算法（蓝色）与MC-CLFV算法（粉色）的计算效率比较图，很明显，蓝框（蚁群算法）的中位数、Q1和Q2都小于粉色框（MC-CLFV算法）。这说明，蚁群算法的计算效率高于MC-CLFV算法。也可以看出，随着扇区数量的增加，两种算法的三个参数之间的差异越来越大。在扇区数量为8的时候，MC-CLFV算法的中位数值（9 856）约为蚁群算法的中位数值（1 006）的10倍。另外MC-CLFV算法需要前期元素空域重组，也需要大量的时间。因此，从计算效率上自顶向下地用Voronoi图切割空域，极大地提高了分扇区的效率。

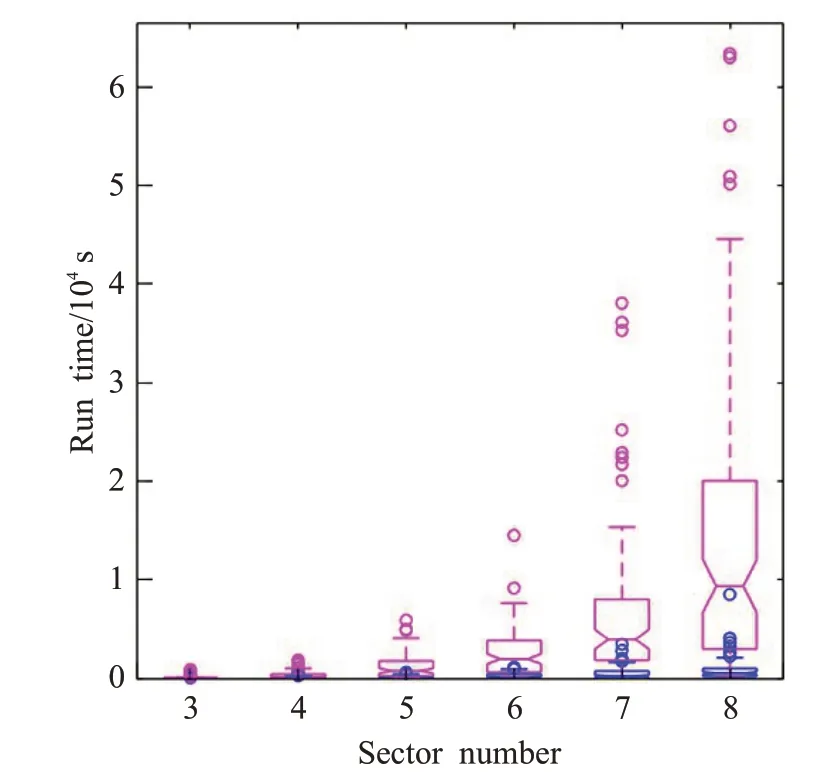
图11 两种算法的计算时间比较Fig.11 Comparison of computing time between two algorithms

3.4 多层规划求解大规模扇区划分的构想

直接用Voronoi图切割空域，至少生成3个扇区，因此2分扇区需要借助其他方法。当需要划分的扇区数量达到9个以上时，采用单层规划，一次成型耗费的时间会比较长，采用蚁群算法大约需要1 h，显然这个计算时间太长。而如果采用双层规划，先把空域分成3个，每一个再分成3个，总共消耗时间相当于4个1分3的时间，大约是4×20=80 s。如果要分成16个扇区，同样第一层采用1分4，第二层再采用1分4，采用蚁群算法总消耗时间是5×30=150 s。虽然研究的空域、算法和文献[22]有很大的不同，但是这篇文章中报道的采用双层规划计算16个扇区大约需要20 min，远远高于推测的计算时间150 s。

如果目标扇区数可分解，多级规划引理如下：

引理1如果空域被划分为n个扇区，并且最多有n个备选方案，且扇区数目可以表示为n=ai×b i×ci，i=1,2,…,m，则三层规划的计算时间计算公式必是：

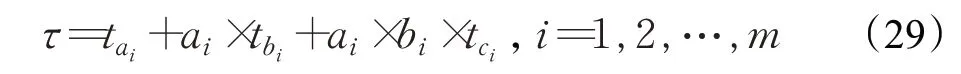
m是可能的数字组合方案数量。在备选方案中，时间最短的方案必定满足以下条件：

t a i是一个空域被分割成a i份空域的计算时间。t b i、t c i和t a i的定义一样。公式中的“|”符号表示条件符号。

对于10个扇区可以双层规划，先借助其他方法2分，再5分。而11、13、17、19这样的数字，可以通过先切割部分扇区或者增加虚拟扇区的形式，变成可分和数来解决。由于篇幅的关系，这个问题留在未来的研究中解决。

4 结论

本文开发了一种用Voronoi图直接切割空域形成管制扇区的方法，模型效率高，能自动满足凸约束、连通性约束和压缩性约束，不需要预处理与后处理。基于航空器在所研究时空范围的4维航迹态势来计算工作负荷计算模型能准确估计管制员的工作任务时间，节约计算时间。本文开发的蚁群算法比基于蒙特卡洛的MC-CLFV算法探索能力强、求解质量高，而且计算时间大大缩短，计算效率得到显著提升。

对于划分9个以上数量的扇区，本文提出了采用双层或者多层规划的解决方案，并推断采用多层规划计算时间会比采用单层规划显著减少，对于多层规划较大奇数个扇区的划分和设计，需要在未来继续研究。