软时间窗多式联运4PL路径问题的改进乌鸦算法

唐怀洞，卢福强，王雷震，王素欣，毕华玲

1.东北大学 信息科学与工程学院，沈阳 110004

2.东北大学秦皇岛分校，河北 秦皇岛 066004

随着我国经济的飞速发展，物流行业也进入发展的快轨道。目前，第三方物流（the third party logistics，3PL）是物流界的主要商业模式，专门从事物流运输服务。然而，随着信息技术的不断发展，3PL也出现了一些缺陷，3PL不能有效地利用各种资源，不能实现供应链的整体优化，单个3PL也难以完成跨区域、跨行业的物流业务。于是，第四方物流（the fourth party logistics，4PL）受到学者们和企业间的广泛关注，4PL是集成管理咨询和3PL服务的集成商，能够根据客户需求提供一套完整的运输方案[1-2]。

4PL的特点决定了4PL路径优化问题不同于传统的车辆路径问题，其需要在选择物流路径的同时选择3PL服务商。一些学者在这一领域展开了相关的研究，但是这些研究大部分仅考虑的是3PL服务商的单一运输方式，忽略了多式联运能够将不同运输方式的优势结合起来，提高运输资源利用率，降低物流运输成本的特点[3]。如黄敏等[4]建立考虑单一运输方式的4PL路径优化模型，并根据问题特点设计混合算法对模型进行求解；Huang等[5]根据不确定性理论建立单一运输方式模糊规划模型，并设计模糊仿真的两步遗传算法来寻找近似最优解。此外，在部分多式联运路径优化问题中，如赖志柱等[6]建立多软时间窗约束的多目标路径优化模型，并设计改进的粒子群算法进行求解，但其将部分中转节点设为软时间窗，货物提前到达将产生存储管理费用，延迟到达产生惩罚费用，而对于目前的多式联运组织来讲，完全可以做到在中转节点进行各种运输方式的无缝对接；杨文东等[7]利用蚁群算法求解了以总运输成本最小为目标，目的节点为硬时间窗的双层优化模型，然而在实际货物运输过程中，由于机械故障、天气状况等随机因素的影响，可能会造成货物不能在客户要求的时间内到达，且运输距离越长，中转节点越多越容易发生，显然，这种硬时间窗数学模型无法应对这种随机情况。

由此可见，在以上研究的基础上，研究目的节点带有软时间窗的多式联运4PL路径问题更具有实际意义和应用价值。目前解决4PL路径优化问题的方法，主要以智能优化算法为主，比较典型的有遗传算法[5，8]、和声搜索算法[9]和蚁群算法[10]等，而乌鸦搜索算法是近年来新兴的智能优化算法，且已经被证明在工程优化方面比遗传算法、粒子群算法等效果更好[11]。于是，本文设计了基于天牛须搜索思想和莱维飞行机制的乌鸦搜索算法对问题进行求解，设计不同节点规模的算例验证模型和算法的有效性。首先通过田口方法得出算法最优参数组合，并与其他算法进行结果比较分析，最后分别研究4PL集成商采用多式联运运输方式具有的优势和软时间窗不同时对实验结果的影响。

1 数学模型

1.1 问题描述

某4PL公司承接了一项运输任务，需要将一批货物从起始节点运送到目的节点，运输网络多重图如图1和图2所示。图2中，数字1、2代表3PL服务商的标号，（1）、（2）、（3）代表3PL服务商的运输方式。每段路径上可能存在多个可以提供运输服务的3PL服务商，每个3PL服务商可以提供多种运输方式。在运输货物时会产生运输费用和运输时间，在中转节点发生3PL服务商运输方式的转换时，会产生中转费用和中转时间。在目的节点设置为客户要求的货物到达时间窗，若货物提前到达，则产生一定的存储管理费用；若延迟到达，则产生一定的惩罚费用。综合上述因素，4PL公司需要确定最佳的运输路径、3PL服务商及其运输方式，使总运输成本最低。

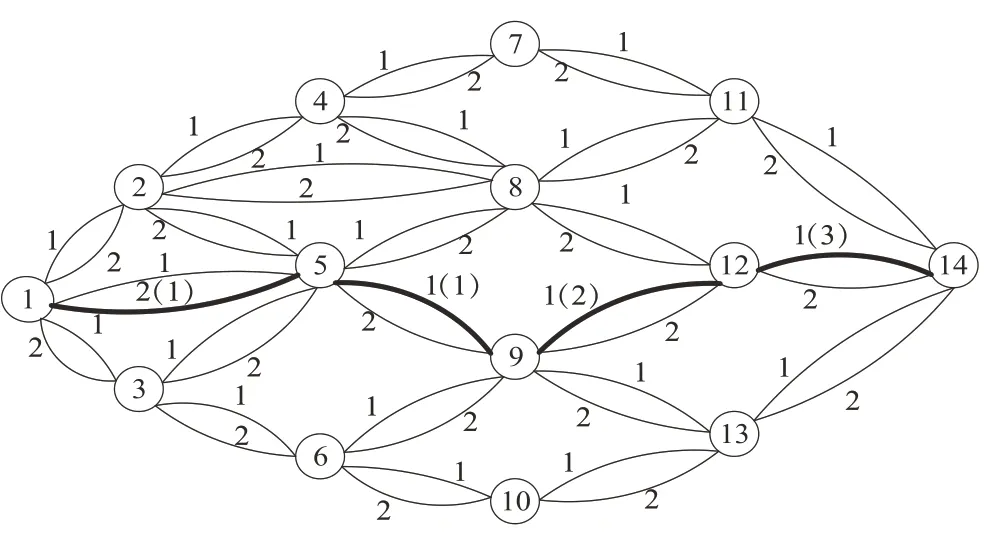
图1 4PL运输网络多重图Fig.1 4PL transport network multiple diagram

图2 节点间运输网络图Fig.2 Transport network diagram between nodes

1.2 模型构建

1.2.1 模型假设

（1）货物在运输路段上不可以更换运输方式，一旦采取某个3PL服务商的运输方式，那么必须到下一个节点才能换成另一种运输方式。

（2）在任何一个中间节点，每个3PL服务商都有满足换装需求的各种运输设备，即在任何中间节点处都可以发生各种运输方式之间的转换。

（3）在中间节点发生运输方式转换时，则只需考虑中转费用和中转时间，不需要考虑其他因素。

1.2.2 模型参数及变量描述

模型参数描述如下：

I为点集合，表示货物运输所经过的节点，i∈I,j∈I；

J为运输方式的集合，表示运输方式的种类，k∈J,z∈J；

r ij为相邻两节点间3PL服务商的数量，i∈I,j∈I；

Q为客户需求量；

C kz j表示在节点j从运输方式k转换成运输方式z需要的单位中转费用；

P E为货物提前到达目的节点，单位时间内需要支付的存储管理费用；

Tmin为客户要求货物从起始节点至达到目的节点的最早时间；S D为货物到达目的节点的时间；

P L为货物延迟到达目的节点，单位时间内需要支付的惩罚费用；

Tmax为客户要求货物从起始节点至达到目的节点的最晚时间；

n为目的节点，n∈I；

决策变量描述如下：

xk ijl表示如果从节点i到节点j采用了第l(l=1,2,…,rij)个3PL服务商的第k种运输方式，那么该值为1，否则为0；

y kz j表示如果在节点j从运输方式k转换成运输方式z，那么该值为1，否则为0。

1.2.3 模型建立

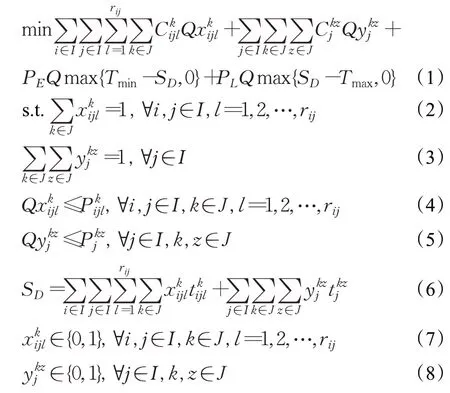
其中，式（1）是该模型的目标函数，表示最小化总运输成

2 算法设计

考虑多式联运的4PL路径优化问题是NP-hard问题，目前的解决方法主要以智能优化算法为主，而乌鸦搜索算法[11]（crow search algorithm，CSA）是2016年提出的一种新兴群体智能优化算法，与其他智能优化算法相比，该算法具有结构简单、参数少、易于学习和掌握等优点，且已经成功应用于多个领域。但是，该算法的两个位置更新策略均存在一定的盲目性，CSA存在求解精度低、收敛速度慢的缺陷。针对这一情况，本文引入代际信息交流机制和天牛须搜索思想对追随领导者产生的位置更新策略进行改进，代际信息交流机制是使乌鸦个体追随上代最优乌鸦个体位置进行移动，弥补了乌鸦个体位置更新盲目性的缺陷，天牛须搜索思想是比较天牛左右两个触角探测到的气味强度来决定下一次的移动方向，提高CSA的寻优能力。针对CSA随机产生位置的更新策略，引入了莱维飞行机制，它的特点是长时间的短距离移动，偶尔长距离移动，可以保证移动不会只停留在某个局部范围，提高算法跳出局部最优的能力。

2.1 编码和种群初始化

根据问题特点，采用双列变长编码机制[12]对乌鸦个体分两段进行编码，第一段表示路径经过的节点集，第二段表示3PL服务商及其运输方式集。采用Dijkstra算法[13]初始化乌鸦种群，首先将4PL运输网络多重图处理成简单网络图，即相邻节点间仅有一个3PL服务商的一种运输方式，然后计算每条边上的权值，计算方式如式（9）：

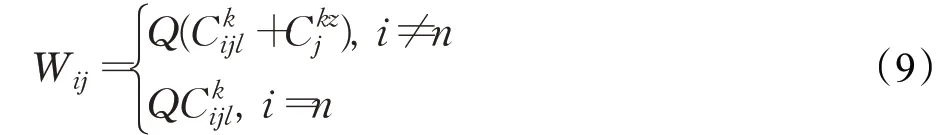
其中，Wij为相邻两节点之间边上的权值，权值的计算为一条路径上的货物运输费用与在节点产生的中转费用之和。若是目的节点，则只需算一条路径上的货物运输费用。

于是，运用Dijkstra算法通过简单网络图求出一个初始解，重复此过程直至达到改进乌鸦搜索算法（levy beetle search algorithm，LBSA）设定的种群规模，从而产生问题的初始种群。

2.2 位置更新策略

利用LBSA的两个位置更新策略进行解的更新，其中位置一更新策略，如式（10）第一个式子，乌鸦个体首先按照加入代际信息交流机制的CSA进行移动，然后将乌鸦个体视为天牛，进行天牛须算法（BAS）的移动。

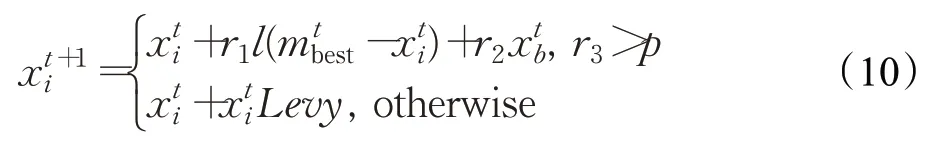
其中，x ti表示第t次迭代中第i个乌鸦的位置，xt+1i表示第t次迭代后第i个乌鸦的位置，r1、r2、r3均是服从[0，1]均匀分布的随机数，l表示第t次迭代中第i个乌鸦的飞行距离，m tbest表示第t次迭代中乌鸦种群的最优位置，即引入的代际信息交流机制，使得乌鸦个体朝着上一代个体最优位置进行移动。xtb表示第t次迭代中按照BAS算法移动的距离，即位置增量，p为转换概率，Levy为遵循Levy飞行的步长：

其中，μ、v服从标准正态分布，β=1.5。

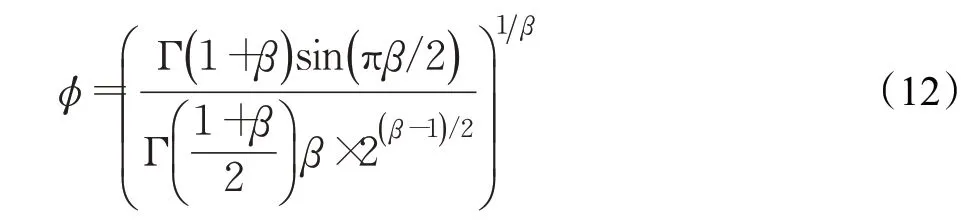
按照天牛须算法移动的位置增量xtb+1更新公式如式（13）：

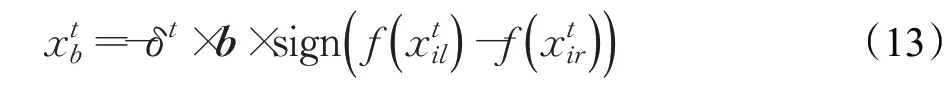
其中，δt表示第t次迭代中天牛的步长，δt=δt-1×eta，eta=0.95，表示步长的衰减系数。表示天牛右触角指向左触角的随机单位向量，rands()为随机函数，k为解的分量个数。sign为符号函数表示天牛左触角位置的适应度值表示天牛右触角位置的适应度值。

天牛左、右触角位置更新公式为：

其中，d t=δt/c，表示两触角之间的距离，c=5。

2.3 适应度函数

将目标函数直接作为算法的适应度函数。若要求的是最小化目标函数，则只需要将解代入适应度函数中，求得的适应度值越小，则解越好，否则则越差。

2.4 算法步骤

LBSA算法步骤如下：

步骤1运用Dijkstra算法初始化乌鸦种群，并初始化种群规模NP，迭代次数NG，飞行距离l等参数。

步骤2根据适应度函数数计算初代个体的适应度值，选择出当代最优解，初代个体的位置即为当前个体的最优解。

步骤3根据产生的均匀分布随机数r3与转换概率p的比较，利用式（10）进行解的更新。

步骤4根据适应度函数计算所有解的适应度值，通过比较，更新个体最优解和种群最优解。

步骤5重复步骤3和4直至到达最大迭代次数NG终止操作。

步骤6输出最优解及其适应度值。

3 算例分析

为了验证本文提出的数学模型和LBSA算法的有效性，设计了三种节点规模的算例，算例规模分别是7节点、14节点和28节点。首先通过田口方法获得算法最优参数组合，然后与BAS、CSA、LCSA算法进行对比分析，验证改进算法的有效性。其次将多式联运与单一3PL服务商的单一运输方式所产生的实验结果进行对比分析，分析得出多式联运能充分发挥不同运输方式的优势，有效降低总运输费用，最后分析不同软时间窗对实验结果的影响。三种节点规模的算例使用的实验数据均参考文献[14]，并根据现实生活中三种运输方式所具有的技术和经济特点进行修改。本仿真实验环境为：Windows10操作系统，主频3.50 GHz，RAM8.00 GB，仿真软件采用Matlab2015b。

3.1 算例描述

某4PL公司承担了一项运输任务，运输货物量为10，要求将货物从起始节点送到目的节点，中间会经过多个城市节点。相邻两节点之间存在两个3PL服务商，且每个3PL服务商可以分别提供三种运输方式，即铁路运输、公路运输和水路运输（部分节点之间存在），每种运输方式的运输费用、运输时间、运输能力会有所不同。在目的节点加入一个软时间窗，提前到达会产生一定的存储管理费用，延迟到达会产生一定的惩罚费用。三种节点规模下的软时间窗范围分别为[35，40]、[50，55]、[81，86]，4PL集成商需要分别选择出一套最小化总运输费用的运送方案。由于篇幅原因，这里仅列出例1的相关数据。

表1中形如x/y/z的数据，其中x为单位费用，y为时间，z为运载能力；表2中数据的分子为单位中转费用，分母为中转时间。提前到达目的节点需要支付货物存储管理费用，单位时间费用为30，延迟到达目的节点需要支付惩罚费用，单位费用为40。

表1 例1运输网络多重图中相邻节点间数据Table 1 Example 1 data between adjacent nodes in transport network multiple graph

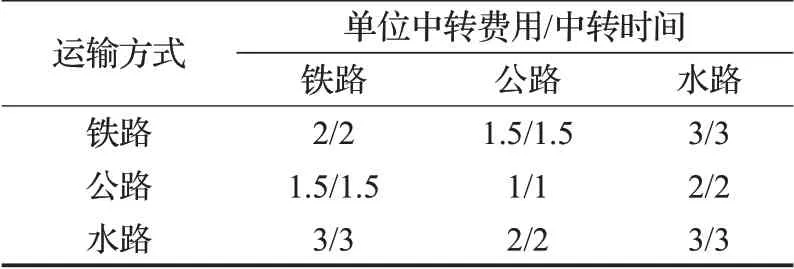
表2 运输方式之间转换情况Table 2 Switching between modes of transport

3.2 算法参数设置

采用田口方法[15]可以确定算法的最优参数组合。为了描述如何确定LBSA的最优参数组合，以14节点规模为例，介绍确定最优参数水平的过程。首先，确定算法的可控参数，分别是迭代次数NG、种群规模NP、飞行距离l、转换概率p、天牛步长δ，然后测试5个参数的不同取值对实验结果的影响，并经多次测试后选取算法性能表现较好的参数水平，如表3所示。

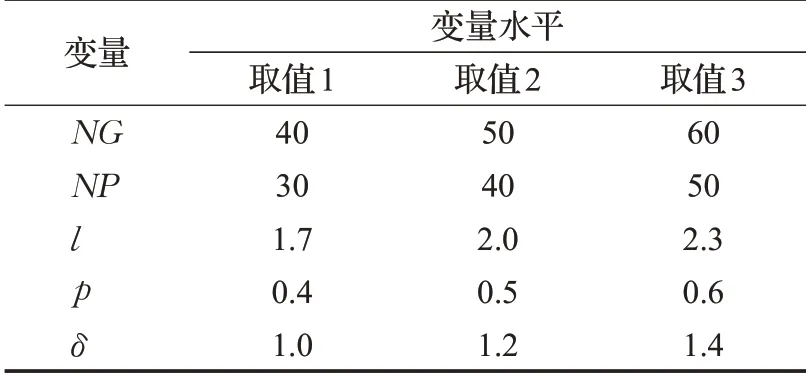
表3 LBSA算法参数及其水平Table 3 LBSA algorithm parameters and levels

按照正交表的创建方法，选取各参数水平的不同组合进行实验研究，将每组参数组合代入到LBSA算法中运行50次，实验结果的平均值放入正交表中，得到实验结果如表4所示。

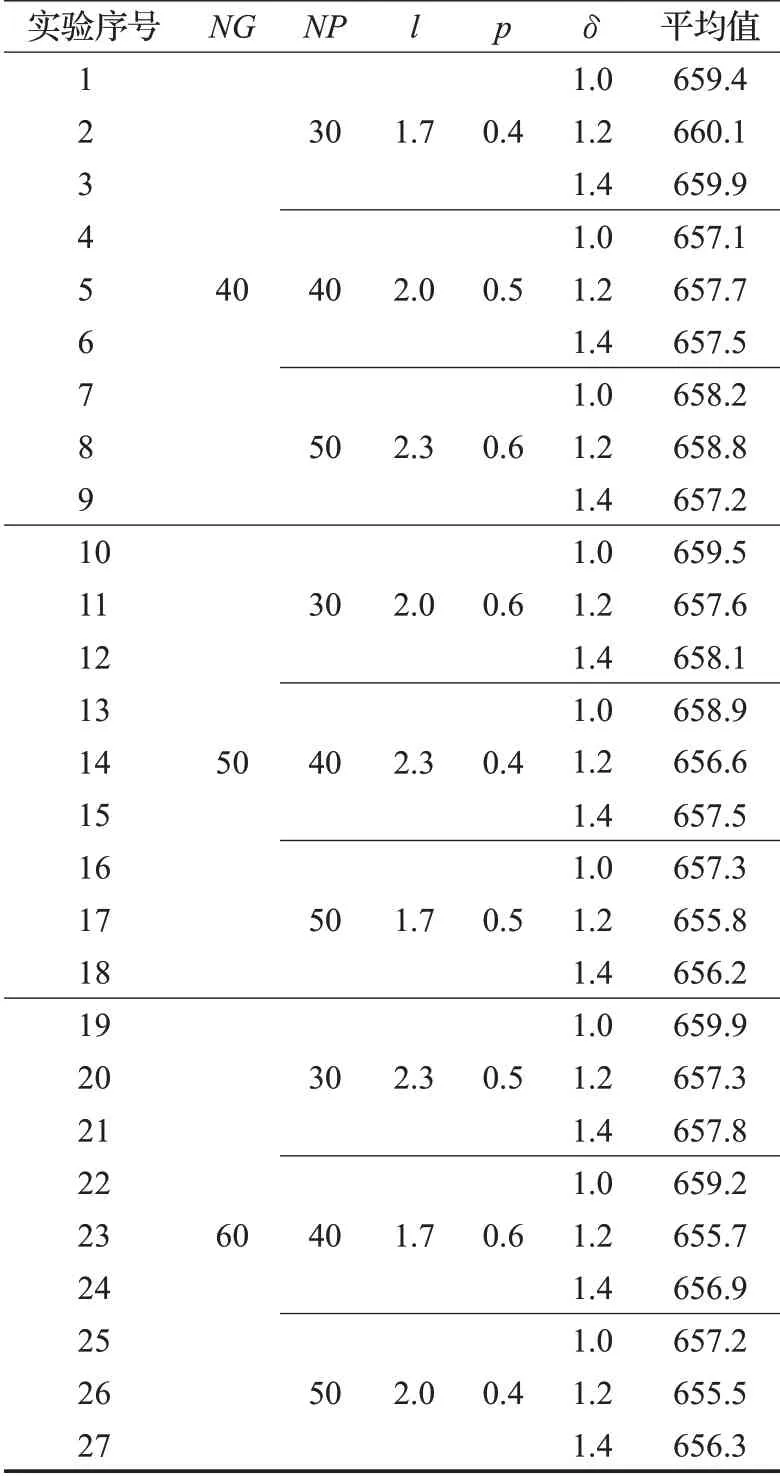
表4 正交实验表Table 4 Orthogonal experiment table

然后运用Minitab17软件分别得到参数的信噪比主效应图和均值主效应图，如图3、图4所示，从图中可以看出，算法参数对信噪比的贡献程度，信噪比的变化趋势，以及参数对实验结果的影响程度和变化趋势。从图3、图4中可以看出，14节点规模算例下LBSA算法的最优参数组合分别为：NG=60、NP=50、l=2.0、p=0.5、δ=1.2。同样，利用田口方法可以得到7节点和28节点的LBSA算法的最优参数组合，如表5所示。

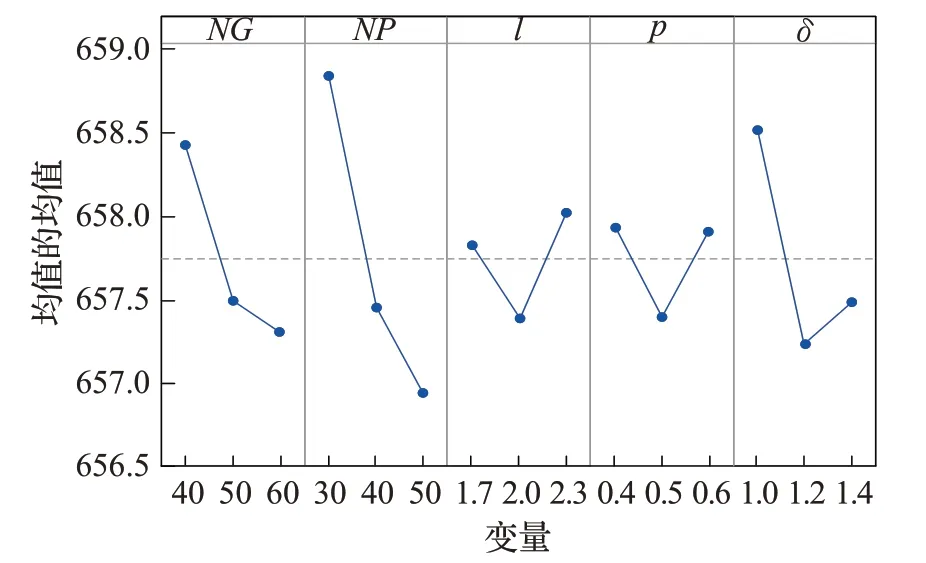
图4 参数的均值主效应图Fig.4 Main effect diagram for means of parameters

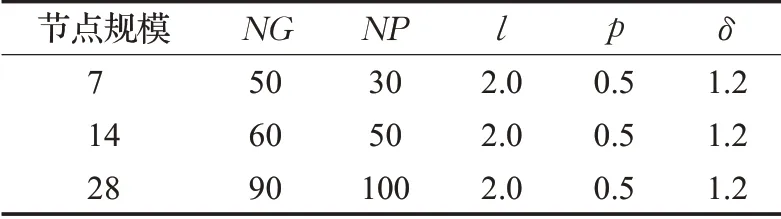
表5 不同节点规模的最优参数组合Table 5 Optimal parameter combination of different node sizes

图3 参数的信噪比主效应图Fig.3 Main effect diagram for SNR of parameters

3.3 算法性能对比分析

针对三种不同规模的实验案例，分别使用BAS、CSA、LCSA、LBSA算法进行运算，每种算法的参数组合都是经过上述田口方法求出，每种算法运行50次，得到的实验结果如表6表示。由表6可知，在计算时间上，BAS算法运行最快，这是因为BAS算法只需要一个个体，而CSA、LCSA和LBSA算法运算时间相差不大。对于7节点规模案例，四种算法都可以求得最优值，但是CSA、LCSA和LBSA算法的最差值、平均值和标准差要优于BAS算法。对于14节点规模案例，BAS算法失效，无法求得最优值，并且CSA、LCSA和LBSA求得的最差值、平均值和标准差都要明显由于BAS算法。对于28节点规模案例，BAS算法依旧失效，虽然CSA、LCSA算法求得了最优值，但最差值、平均值和标准差要较明显差与LBSA算法。并且由表6可知，随着节点规模的增大，LBSA算法的达优率和稳定性要远高于BAS和CSA、LCSA算法。上述实验结果证明LBSA算法在解决本文4PL路径问题具有一定的有效性和优越性。

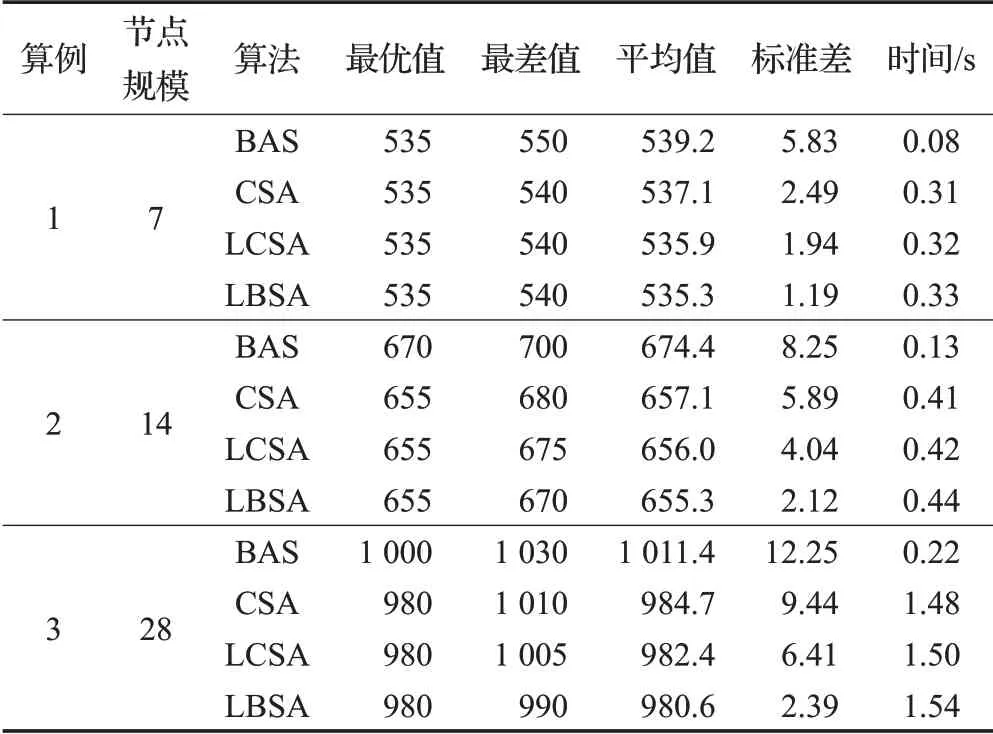
表6 算法实验结果对比Table 6 Comparison of algorithm experimental results

3.4 实验结果分析

运用LBSA算法求出三个算例下的最优运送方案，如表7所示。以算例2为例，介绍4PL公司为客户选择的运送方案。当客户要求货物到达目的地时间范围为[50，55]时，货物依次经过的城市节点为1、5、9、12、14，相邻城市节点间依次选择编号为2、1、1、1的3PL服务商，运输方式依次为各3PL服务商的铁路运输、铁路运输、公路运输和水路运输，如图1中加粗线所示。运用LBSA算法求得的三个算例结果收敛过程如图5、图6、图7所示。

表7 不同节点规模下LBSA算法最优运送方案Table 7 LBSA algorithm optimal transportation scheme at different node sizes

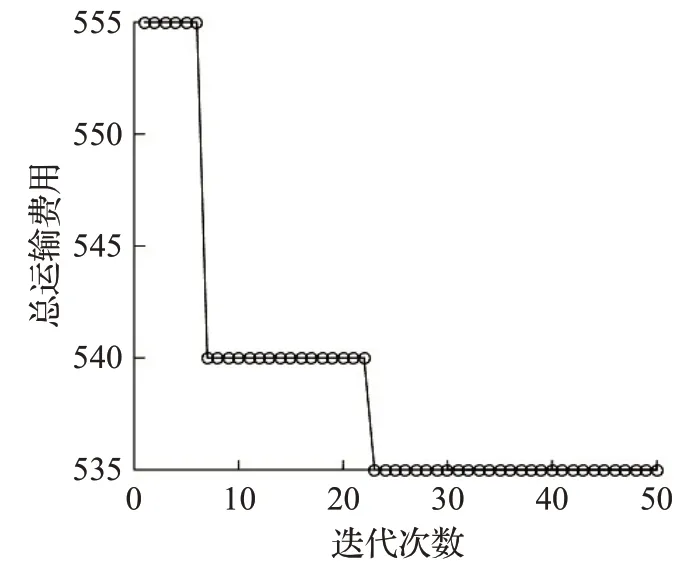
图5 算法收敛过程（算例1）Fig.5 Algorithm convergence process（example 1）

图6 算法收敛过程（算例2）Fig.6 Algorithm convergence process（example 2）

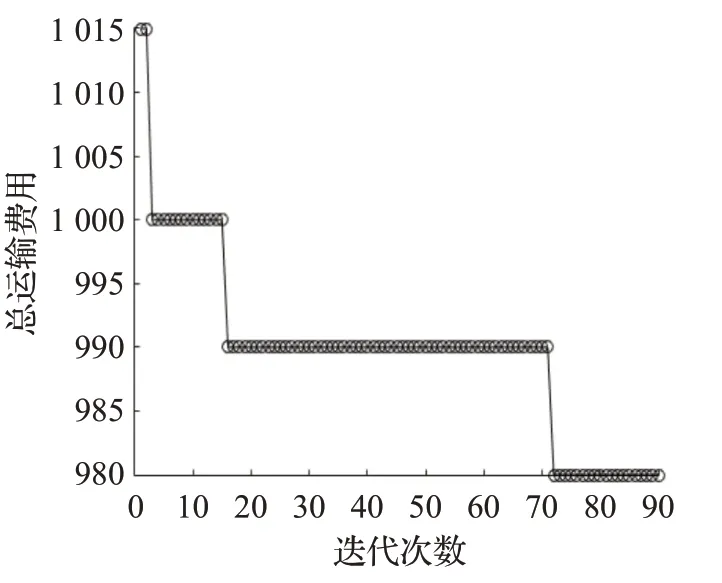
图7 算法收敛过程（算例3）Fig.7 Algorithm convergence process（example 3）

3.5 结果对比分析

为了更直观地分析4PL公司通过不同3PL服务商采用多式联运来降低总运输费用的优势，对表7中三种节点规模下的软时间窗，分别画出不同3PL服务商采用多式联运与单一3PL服务商采用单一运输方式所需总运输费用的对比图，如图8、图9和图10所示。由于水路运输只存在于部分城市节点，故不做分析，同时计算出各运输方式所需的总运输时间，如表8所示。

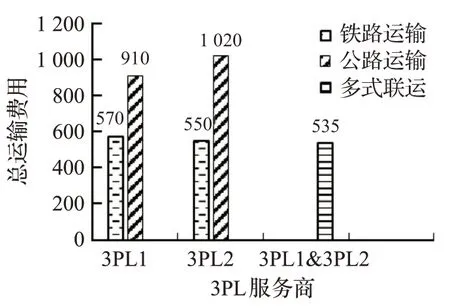
图8 7节点运输方式对比图Fig.8 Comparison diagram of transportation mode of 7 nodes

图9 14节点运输方式对比图Fig.9 Comparison diagram of transportation mode of 14 nodes

图10 28节点运输方式对比图Fig.10 Comparison diagram of transportation mode of 28 nodes

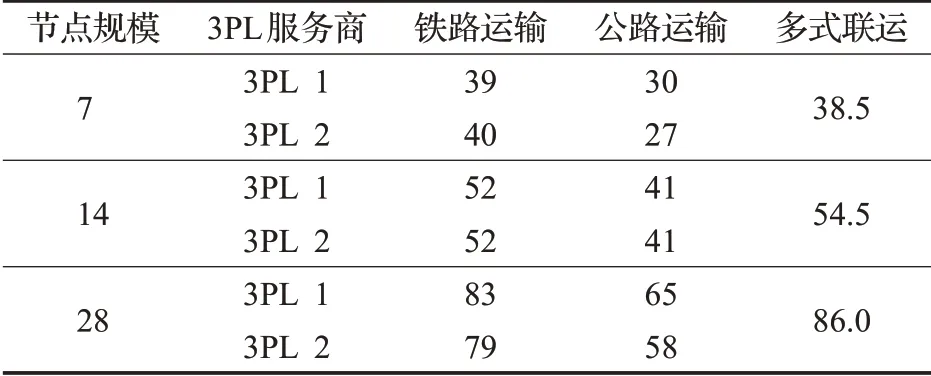
表8 各运输方式所需运输时间Table 8 Transportation time required by each mode of transportation

3.6 软时间窗对实验结果的影响

从图8、图9、图10和表8中可以看出，虽然单一3PL服务商使用铁路运输和不同3PL服务商采用多式联运运输所需运输时间相差不多，但运输总运输费用要比使用多式联运运输高。尤其是当单一3PL服务商使用公路运输时，由于提前到达客户要求时间过多，产生了大量的货物存储管理费用，导致总运输费用偏高。从以上分析可以看出，4PL集成商采用多式联运的运输组织形式，能够在满足客户要求的同时，有效地降低总运输费用。因此，采用多式联运能够更好地为4PL集成商提供决策依据。

分析软时间窗不同时对最优运送方案的影响。在分析软时间窗对实验结果的影响之前，先对无软时间窗约束条件下的问题进行求解，即将数学模型中的存储管理费用和惩罚费用公式去掉。求得28节点规模下的最小总运输费用为900，花费时间99。以上述求得的时间为临界点进行软时间窗的划分，来分析软时间窗对实验结果的影响，如表9所示。

从上述表中可以看出，随着客户对软时间窗要求的范围越来越小，4PL集成商会确定不同的最优运送方案，方案所需总运输费用也越来越高。当客户要求的软时间窗范围过小时，比如表9中软时间窗范围为[52，57]时，最优运送方案花费时间为58，同时58也是运输网络图中所有运送方案花费时间最小者，如果研究的问题是硬时间窗，建立硬时间窗的数学模型，那么显然无法解决这种情况，研究软时间窗的路径问题则更具有实际意义。在这些最优运送方案中，由于客户要求的软时间窗不同，尽管4PL集成商可能会选择相同的运输路径，但3PL服务商及运输方式的选择会有所不同。这是因为4PL集成商能够针对客户不同的软时间窗要求，及时做出决策，得到最优的运输路径、3PL服务商及其运输方式的组合。

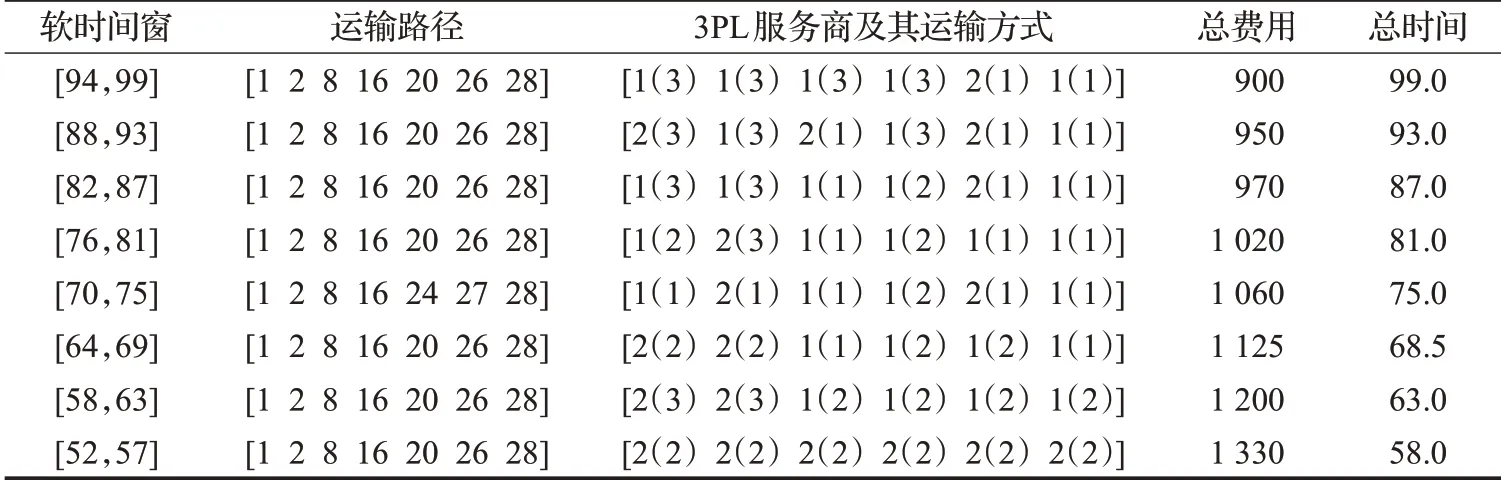
表9 例3软时间窗对结果的影响Table 9 Example 3 effect of soft time window on result

4 结语

（1）考虑机械故障、天气状况等随机因素在运输过程中对各种运输方式的影响，多式联运能够发挥各种运输方式的优势，建立软时间窗的多式联运4PL路径优化模型。

（2）设计引入天牛须搜索思想和莱维飞行机制的乌鸦搜索算法对其进行求解。通过三种不同规模的算例验证了LBSA在解决此问题时的有效性，扩展了此算法的应用领域。

（3）通过实验结果对比分析得出，在满足客户的需求下，4PL集成商采用多式联运的运输方式相比单一3PL服务商采用单一运输方式可以有效降低总运输费用。接着以例3为例，分析了客户要求的软时间窗不同时，4PL集成商会确定不同的最优运送方案。

（4）本文还有一些不足之处，比如未考虑货物量过多，超过任何一个3PL的任一运输方式运载量的情况，在以后的研究中可以从这一角度出发。