多相机与IMU融合的室外机器人定位方法研究
董 荣,厉茂海,林 睿,刘仕琦,丁 文
苏州大学 机电工程学院,江苏 苏州 215021
在人类社会和科技水平不断进步的背景下,信息技术、人工智能、互联网、机械电子等相关产业取得快速发展,室外移动机器人在工业和生活中的应用也越来越多。机器人的状态估计问题一直是研究热点。SLAM技术也就是同时定位和地图创建,是实现室外移动机器人自主定位移动导航的关键技术。近年来,由于相机具有廉价、采集信息丰富、重量轻、安装方便、易于与其他传感器融合等优势,基于视觉的SLAM方法受到研究生的广泛关注,大量的相关方法也应运而生。
纯视觉SLAM常用的包括单目、双目以及RGBD相机。Mono SLAM[1]是2007年提出的基于单目视觉的SLAM框架,后端使用基于EKF(扩展卡尔曼滤波)的方法,追踪前端稀疏的特征点,以相机的当前状态和所有路标点为状态量,更新其均值和协方差。PTAM[2](parallel tracking and mapping)首次区分出前后端,是第一个使用非线性优化作为后端的方案。DTAM[3](dense tracking and mapping)、LSD-SLAM[4](large-scale direct monocular SLAM)、SVO[5](fast semi-directmonocular visual odometry)、DSO[6](direct sparse odometry)等都是基于直接法的单目或双目SLAM方案。ORBSLAM[7-8]相比之前的工作,支持单目、双目、深度相机三种相机模式,该系统主要使用了跟踪、地图构建、闭环检测三个线程。由于其应用广,结构完善,被认为是现代视觉SLAM系统中最为经典的系统之一。
而视觉部分,无论是单目、双目还是RGBD相机均具有朝向单一、采集视野有限、受遮挡、信息不充分等缺点,研究表明,使用多相机可以有效地提高视觉SLAM的性能。2003年,Pless等人首次实现了在SFM领域使用多相机系统[9]。随后,Ragab[10]基于EKF,在机器人上放了两对背对背的立体相机实现了SLAM问题。Kaess等人[11]基于Harris角点[12]提出了多相机的SLAM系统。2013年,Lee团队在无人驾驶领域使用了多相机系统[13],实现了无人车的自定位。Harmat使用多相机对PTAM性能进行了改善[14],改进了透视相机模型并在无人机上安装了一个朝地的立体相机和一个朝天的广角相机,提出了经典的MCPTAM(multi-camera parallel tracking and mapping)方法[15]。Tribou同样基于PTAM以及MCPTAM的方法研究了具有非重叠视场角的SLAM方法[16],改善了无人机定位的鲁棒性。此外,Urban等人[17]基于ORBSLAM开展相关研究,国内杨绍武等人通过配置相机个数和朝向提高了无人机系统的鲁棒性[18-19]。
多目SLAM受益于多相机不同朝向下信息的丰富性,改善了单、双目相机的SLAM方法的鲁棒性,尤其在面对弱纹理以及视线受到遮挡的情形下。然而仅使用多相机无法改善图像模糊,运动过快等缺陷。视觉与惯导融合后能弥补纯视觉下快速运动、图像模糊、过度曝光造成的定位精度低、运动丢失的缺点。视觉与IMU(惯性测量单元)融合的算法有MSF[20](multi-sensor fusion)、OKVIS[21]、MSCKF[22](multi-state constraint Kalman filter)、ROVIO[23](robust visual inertial odometry)、VINS等[24]。其中VINS Fusion支持多种视觉惯性传感器类型(单目摄像机+IMU,双目摄像机+IMU,甚至仅限单目双目摄像机)。相机和IMU具有良好的互补性,高频率IMU可以弥补快速运动对相机的影响,反之相机能够有效修正IMU的漂移。
本文在此基础上,提出了一种基于VINS-MONO算法的多目视觉与惯导紧耦合的定位方法MCSI-VINS,在数据预处理阶段提出了一种基于队列数据结构构建缓冲区的方法,并创新性地提出了一种在线的根据主相机的多相机初始化方法,前端使用Harris角点和LK(Lucas-Kanade)光流跟踪。后端使用基于滑动窗口的非线性优化的方法。此次工作在后端部分增加了多相机的误差项,误差项中增加了时间戳的优化。此方案为室外移动机器人的长期、大规模定位问题提供了保障。最后通过实验验证了本文提出的算法较一些单目、双目与IMU结合的算法相比,鲁棒性更强,精度更高。
1 方法流程
本文提出的多目视觉与惯导紧耦合的定位方法中,多相机提供丰富的视觉信息,惯性测量单元提供高频率运动信息。方法流程大体分成三步,数据预处理、多目VIO联合初始化,优化定位。如图1所示,红色虚线方框部分为数据预处理阶段,此阶段的视觉处理部分对采集到的第一帧图像进行Harris角点的提取并对之后每一帧进行光流追踪,此阶段的IMU部分对数据进行预积分。数据预处理的结果传递给下一模块。在初始化模块中,首先是主相机的视觉惯性联合初始化,对光流跟踪得到的特征点进行处理,求解帧与帧之间位姿的变换,融合IMU预积分信息后最终可以得到尺度信息并将所有量拉到世界坐标系下,完成主相机初始化。随后根据主相机来完成多目相机与惯性的联合初始化。在优化定位模块,基于滑动窗口对视觉重投影误差以及IMU误差进行紧耦合联合优化,其中增加了其他相机的误差项并对时间戳也进行了在线的优化,不仅保证了系统的鲁棒性,也能够更加精确得到机器人位姿。
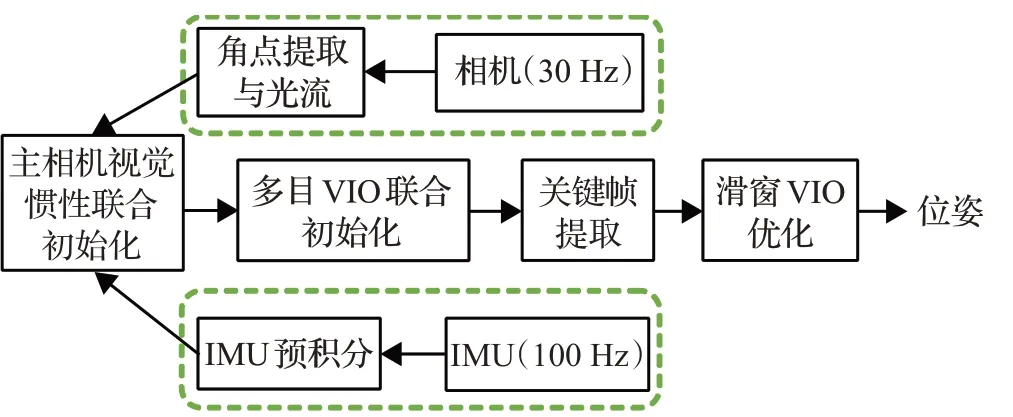
图1 多目视觉与惯导融合方法流程图Fig.1 Flow chart of multi-vision and inertial navigation fusion method
2 数据预处理
2.1 视觉处理部分
多目相机采集到的图像信息丰富,在视觉处理部分,各个相机独立采集图像并进行数据处理。接下来以主相机为例,简述主要流程。首先,对第一帧图像进行Harris角点的提取。随后对之前图像进行LK金字塔光流跟踪,在这个过程中,若光流跟踪成功,则该特征点被跟踪次数增加1,反之被剔除,并通过基础矩阵剔除外点。基础矩阵为一幅图像上一个点到另一幅图像上对极线L的一种映射。一般地,从匹配的点对中选择8个点,使用归一化估算出基础矩阵F,随后计算其余点对到其对应对极线的距离,如果距离小于阈值则为内点,否则为外点,迭代k次当某次去除外点后内点的数目占总数目的比例大于95%时,停止迭代。接着,寻找新的特征点进行数量的补齐,同时通过设置mask来保证特征点均匀分布。最后,对特征点进行去畸变矫正和深度归一化,计算出角点速度,将上述特征点的相关信息传递给下一模块。
在视觉处理过程中,其余相机同时进行数据预处理工作,在这里,提出了一种利用队列这种数据结构,构造缓冲区的方法,由此来解决数据匹配问题。
2.2 IMU预积分
IMU部分,加速度计获得机器人运动的加速度,陀螺仪获得角速度。由于外部存在噪声,将IMU的真实值记为ω、a,测量值记为、,则有:

上标g表示陀螺仪,a表示加速度计,w表示世界坐标系world,b表示IMU坐标系。
将相邻图像时间间隔内的IMU数据进行积分就可以得到这段时间内机器人位姿的变化。预积分使得和IMU测量值无关的部分无需重复积分计算,大大降低了计算量。预积分量仅仅跟IMU测量值有关,表示如下:

在IMU数据预处理阶段,使用中值积分的方法计算离散时间的IMU预积分值,还计算了测量状态的协方差矩阵以及计算了预积分残差对旋转四元数,速度和位移的雅可比矩阵。
至此数据预处理完成,进入下一模块。
3 多目视觉IMU联合初始化
3.1 主相机视觉惯性联合初始化
默认选取前相机作为主相机,如果当前相机提取的特征点数量小于一个阈值时,包括相机受遮挡的情况,则通过判断当前时刻各相机特征点数量而定,此时选取特征点最多的相机作为主相机。
基于主相机的初始化流程图如图2所示。
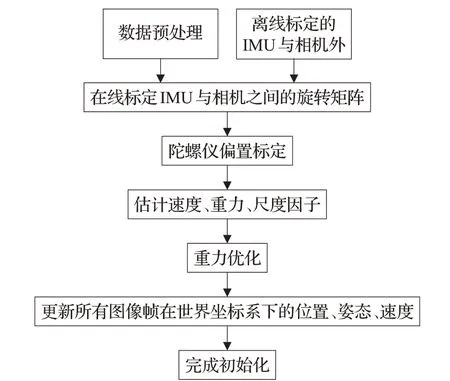
图2 主相机初始化流程图Fig.2 Main camera initialization flow chart
假设前端能够跟踪到足够多的特征点,帧与帧之间的相机之间的旋转变换可以通过滑动窗口的SFM(structure from motion)、经典五点算法、三角化、PNP(perspective-n-point),在滑动窗口中进行整个BA(bundle adjustment)的优化调整得到。与此同时可以通过IMU陀螺仪数据预积分得到相对应的旋转变换。下面的式子表示任意两帧k、k+1之间可以有两条“路径”来得到两帧之间的旋转,这里用四元数表示旋转。
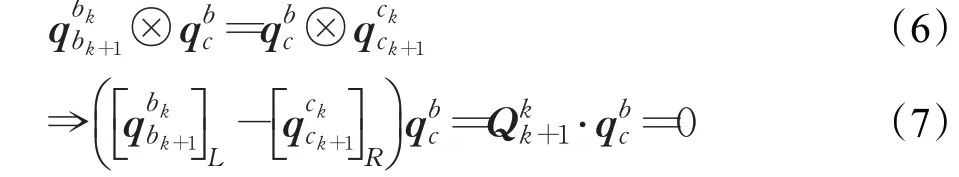
将多个时刻线性方程式(7)累计起来,并加上Huber鲁棒核权重得到:
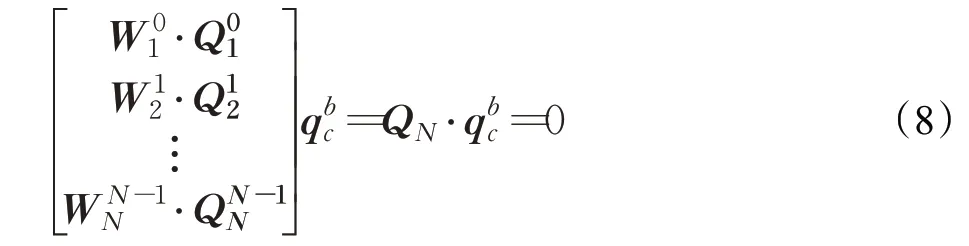
其中权重计算的依据为两条路径的接近程度,这里用旋转轴与旋转角来衡量。旋转角度误差为:
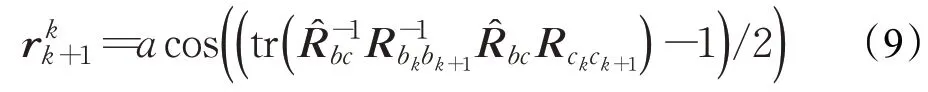
Huber鲁棒核权重为:

公式(8)采用SVD分解,即最小奇异值对应的奇异向量。可以得到相机与IMU之间的旋转约束。利用在线标定的相机与IMU之间的外参以及离线标定的外参,可估计陀螺仪bias,通过求解一个最小二乘得到:
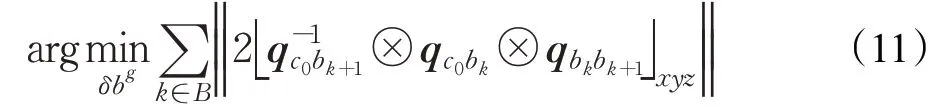
对于n维变量x∈Rn,寻找一个最优值x*使代价函数F()
x取最小值,代价函数通常具有如下形式:

至此可以将第一帧图像坐标系下的所有变量都转换为世界坐标系下的值,并把相机平移和特征点尺度恢复到米制单位,完成一个相机的全部初始化。
3.2 基于主相机的多目VIO联合初始化
上一节求得的世界坐标系与主相机第一帧相机坐标系之间的旋转矩阵记为。除了在线标定和离线标定主相机与IMU之间的外参外,其余相机的外参也被在线和离线标定同时被优化。优化得到的任意相机与IMU之间的外参记为T b c j,这里用j来代表第j个相机。通过对齐重力方向求得的不同相机第一帧相机坐标系与世界坐标系的旋转矩阵,这里要注意世界坐标系并非同一个,因此提出了一种基于主相机的多目初始化方法。
利用主相机,将所有不同相机中的位置、姿态、速度都转化到同一个世界坐标系下,推导公式如下:

至此,完成多目与IMU的联合初始化。
4 优化定位
随着移动机器人不断像新环境探索,就会有新的相机姿态以及看到新的特征点,最小二乘残差就会越来越多,信息矩阵越来越大,计算量将不断增加。为了保持优化变量的个数在一定范围内,使用滑动窗口算法来动态移除变量。初始化之后,执行一个基于滑动窗口的紧耦合多目VIO,得到精度更高鲁棒性更好的状态估计值。在优化中还增加了其他相机的误差项并对时间戳也进行了在线的优化。
4.1 基于滑动窗口的非线性优化
初始化之后,执行一个基于滑窗的紧耦合多目VIO,得到精度更高鲁棒性更好的状态估计值。与3.2节中的推导过程类似,可以求出世界坐标系与IMU坐标系之间的外参

其中,c1为主相机。在建立多目VIO状态量以及残差方程时,都以IMU坐标系作为参考系,不同的相机尽管优化的状态量以及残差方程完全不相同,但求得的状态量的增量也就是机器人的运动姿态几乎是相同的。
使用基于滑动窗口的紧耦合VIO,滑窗中的状态向量定义为:
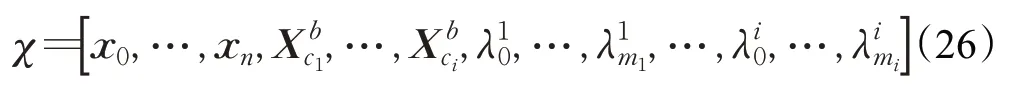
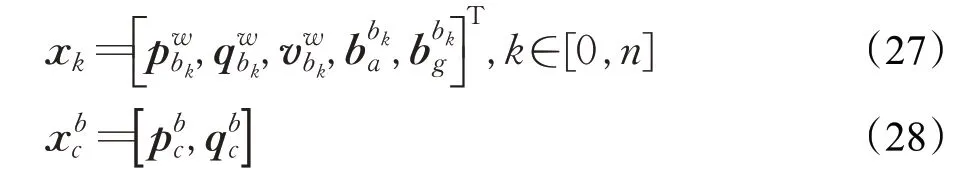
x k是某一时刻捕获第k帧图像时IMU的状态。多目滑窗状态变量共包括滑动窗口内的n+1个IMU的状态,所有相机和IMU的外参,不同相机下mi+1个3d点的逆深度。目标函数如下:
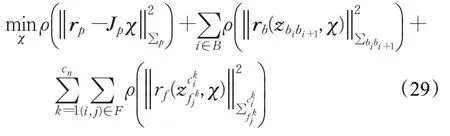
其中三个残差项分别是边缘化的先验信息,IMU测量残差,视觉的重投影残差,cn为相机的个数。
4.2 在线优化时间戳
基于相机与IMU发布频率不同,相机IMU触发的延迟,相机图片传输的延迟,相机与IMU不同的时钟以及相机曝光时间等因素,即使在系统运行前进行了时间戳的标定,也很难保证时间戳的同步,从而造成IMU预积分时间段错误导致里程计的失效。通过将时间差纳入到重投影误差中与IMU积分误差一同优化来实现时间差的在线标定,是削减IMU与相机时钟差对VINS精度影响的最佳方案。
假设在很短时间内,特征点的速度是恒定的。如图3所示,在k时刻,相机检测到这个点,在下一时刻又检测到了这个点记为,则特征点的速度可表示为:

图3 相邻时刻特征点速度Fig.3 Velocity of characteristic point at adjacent moments
用这个速度对观测进行补偿可表示为:


将i时刻的观测进行补偿后得到,在图4中以黄点表示,再反投到j时刻的图像中,得到新的补偿后的反投点,记为,在图4中以红点表示。原先j时刻的观测也进行时间戳的补偿,得到的点记为,在图4中以绿点表示,则新的残差可表示为:

图4 时间戳补偿构建残差示意图Fig.4 Timestamp compensates for build residuals

5 实验
本文的前几部分介绍了多目视觉与惯导紧耦合的定位方法的数据预处理、初始化以及优化定位模块。本章对上文提出的方法进行实验,展示了本文提出的多目和惯导融合的方案MCSI-VINS的实验结果,并且对实验结果进行对比分析。
5.1 实验介绍
本实验使用的室外机器人移动平台通过无线键盘人工遥控,时间延迟小,可以做到实时控制。图5为安装在小车上的多目相机示意图,面向车前的相机为小觅彩色版S2110-95/Color,一左一右为小觅S1030。

图5 相机安装位置Fig.5 Location of camera
为了更好地分析本文提出的MCSI-VINS和经典的VINS双目和单目算法精度的优劣,实验录制了两个不同的数据集。在数据集1中,小车围绕某产业园行驶了约600 m的小圈并回到初始位置。在录制过程中,人为加入了一些使环境更为复杂的因素。如,行人的遮挡、车辆的快速通过、遇到障碍物突然停止、接近于纯旋转的转弯等。在数据集2中,小车围绕同一产业园行驶了约1 800 m的大圈并回到初始位置。与数据1完全相反,在录制过程中,尽量保证了环境因素的稳定。
5.2 实验结果
为了更简单地表示各个算法、约定,经典的VINS双目算法简称为2CVIO,VINS单目算法简称为1CVIO,本文提出的MCSI-VINS简称为MCVIO。RTK-GPS得到的轨迹为真实轨迹,用groundtruth表示。在本章节的图中,各自算法得到的轨迹也遵循上述约定表示。
实验结果将算法得到的机器人运动轨迹和真实轨迹进行对比来评价。本文采用绝对轨迹误差(absolute trajectory error,ATE)来对比,也称为绝对位姿误差(absolute position error,APE)。原理为将算法解算的轨迹与真实轨迹进行绝对距离评估,两者以一定的标准对齐,然后计算偏差。同时,基于计算绝对位姿误差,用RMSE的大小来评估最终算法的精度。也就是计算所有时间上的均方根误差(root mean square error,RMSE)。
5.2.1 小圈复杂环境实验结果
该实验使用数据1进行实验。利用1CVIO、2CVIO、MCVIO得到的机器人位姿轨迹和GPS得到的groundtruth轨迹如图6(a)所示。其中蓝色为单目V
IO算法得到的轨迹,绿色为双目VIO算法得到的轨迹,红色为本文提出算法的轨迹,虚线为GPS的轨迹。根据图6(a)可以直观地看出单目VIO算法由于复杂的数据集环境,其估计的机器人轨迹与真实的轨迹相差较大,而双目VIO和本文提出的算法得到的轨迹和真实轨迹较为接近。注意后半段,红色和虚线仍然保持着高度的重合,而双目VIO算法也由于IMU累计误差产生了些许的漂移。
如图6(b)的evo结果显示,双目VIO算法的RMSE为1.71 m,平均误差为1.42 m,其他参数如表1所示。如图6(c)的evo结果显示,多目VIO算法的RMSE为1.56 m,平均误差为1.09 m,其他参数如表1所示。可以看到和双目的算法相比,多目VIO算法在初始阶段的误差较大,这与双侧两个相机的初始化不充分有关,在后续的运行中明显比双目算法更稳定,最后的累积漂移也明显减少。总的来说,在复杂的环境下,多目VIO算法的各项参数Mean、Median、Min、RMSE均低于双目VIO算法,算法鲁棒性更强,定位精度更高。要注意的是,多目的最大值Max和标准差Std都大于双目,多目的最大值出现在一开始,是由于录制的数据集并没有一个良好的初始化而造成。而由于离散程度的不同,多目的最大值与平均值相差较大而造成Std也偏大。但总的来说,多目VIO算法更优。
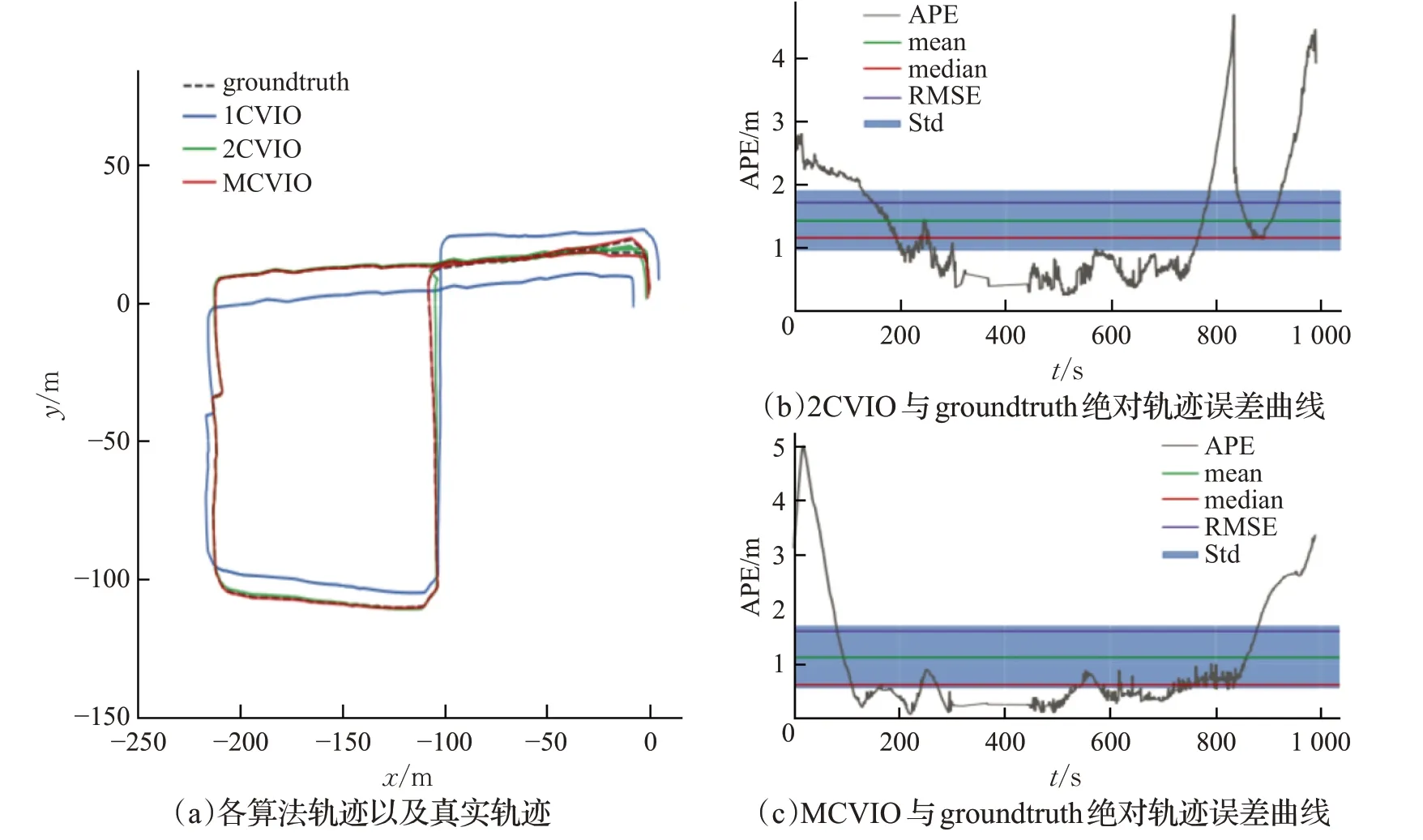
图6 数据1实验结果Fig.6 Experimental results of data 1

表1 双目多目VIO与真实轨迹的绝对轨迹误差的各项参数(数据1)Table 1 Parameters of absolute trajectory error between binocular multivision VIO and groundtruth(data 1)m
5.2.2 大圈简单环境实验结果
该实验使用数据2进行实验。利用1CVIO、2CVIO、MCVIO得到的机器人位姿轨迹和GPS得到的groundtruth轨迹如图7(a)所示。其中红色为单目VIO算法得到的轨迹,蓝色为双目VIO算法得到的轨迹,绿色为本文提出算法的轨迹,虚线为GPS的轨迹。根据图7(a)可以直观地看出,单目VIO算法于简单稳定的环境下,其轨迹与真实轨迹相比复杂环境更为相近,但由于其初始化不充分而造成单目VIO算法与其余算法相比仍旧存在定位精度上的差距。而双目VIO和本文提出的算法得到的轨迹和真实轨迹较为接近。绿色轨迹和虚线始终保持着高度的重合,而双目VIO算法也由于IMU累计误差产生了些许的漂移,在各个转弯时漂移稍大。

图7 数据2实验结果Fig.7 Experimental results of data 2
虽然可以直观地看出单目VIO算法的定位精度明显不佳于其余算法,但却无法明确地看出双目VIO和多目VIO的优劣。如图7(b)为双目VIO算法和真实轨迹的evo评估结果,双目VIO算法的RMSE为2.78 m,平均误差为2.48 m,其他参数如表2所示。

表2 双目多目VIO与真实轨迹的绝对轨迹误差的各项参数(数据2)Table 2 Parameters of absolute trajectory error between binocular multivision VIO and groundtruth(data 2)m
如图7(c)所示为文本提出的多目VIO算法和真实轨迹的绝对轨迹误差曲线,结果显示,多目VIO算法的RMSE为1.08 m,平均误差为0.94 m,其他参数如表2所示。可以看到和双目的算法相比,多目VIO算法在初始阶段仍存在初始化偏移大的问题,此时APE最大为3.38 m。在后续的运行中明显比双目算法更稳定。总的来说,在简单稳定的环境下,多目VIO算法的各项参数Max、Mean、Median、Min、RMSE均低于双目VIO算法,算法鲁棒性更强,定位精度更高。要注意的是,与上个数据集实验结果不同,多目的最大值Max与标准差Std均优于双目,此处双目的Max出现于路程的后半段,Max值是多目的两倍之多是由于机器人运行时间长、IMU累积误差造成。而初始阶段,多目VIO最大值Max还是由于初始化不良造成。
6 结束语
在未知环境下的定位问题中,本文针对单目相机在室外复杂环境下易受到遮挡、相机移动过快、图像模糊以及机器人纯旋转下算法精度和鲁棒性下降、低精度IMU的累积偏移等问题,提出一种多目相机与IMU融合的方案。首先在数据预处理阶段提出了一种基于队列数据结构构建缓冲区的方法,并创新性地提出了一种在线的根据主相机的多相机初始化方法,前端使用Harris角点和LK光流跟踪。后端使用基于滑动窗口的非线性优化的方法。此次工作在后端部分增加了多相机的误差项,误差项中增加了时间戳的优化。此算法保证了系统的鲁棒性,也能够更加精确得到机器人位姿。
通过两个不同的数据集对MCSI-VINS进行测试,得到以下结论:
(1)多目相机可以提供一个更广阔的视野,提供了不同方位的特征点信息,在某相机被遮挡的情况下,仍能保证定位算法的准确性和鲁棒性。
(2)本文提出的MCSI-VINS方法不论室外是简单稳定的环境还是复杂环境,较经典的单目、多目VINS算法来说,其鲁棒性更好,定位精度更高。
(3)对于数据集的录制,给本文提出的算法一个更好的初始化过程能够使其性能发挥更好。

