干热环境喷射用纤维混凝土力学性能及孔隙结构分析

崔圣爱 符 飞 曾 光 陈 振 李固华

(西南交通大学土木工程学院， 成都610031)

随着设计理论和施工技术的进步，隧道建设逐渐向长大深埋方向发展，伴随而来的高地温问题也日益突出[1-3].隧道高地温主要以2种形式出现：①干热，即在地质构造较好的地方，地质层内部热量通过岩石传到隧道表面；②湿热，即在断裂破碎、断裂转折复合及岩石破碎地段，裂隙发育程度高，地下热水富集形成温泉.实际工程调研表明，在高地温隧道中，干热环境普遍存在[4-5].同时，现场施工监测和前期研究均表明，高地温环境会使喷射混凝土性能劣化，甚至导致混凝土脱黏开裂，隧道的初期支护质量难以得到保证.高地温隧道中干热环境普遍存在，在该环境中喷射混凝土快速升温与失水，水泥基材料微细观结构劣化，混凝土干缩增大，加剧了混凝土裂纹的产生与发展.喷射混凝土作为初期的安全防护，其开裂问题关系到支护结构安全性和耐久性的有效发挥.

文献[6-10]研究了高地温湿热环境对喷射混凝土性能的影响及改善措施；文献[11]分析了高地温环境下喷射混凝土的变形性能；文献[12-13]研究了高地温干热环境对喷射混凝土-岩石黏结强度的影响规律；文献[14]指出材料的微观结构决定着宏观性能.混凝土材料是具有复杂结构的非均质、多相(气、液、固)和多层次(微观、细观、宏观)的复合材料体系，其宏观物理学行为所表现出的不规则性、不确定性、模糊性和非线性等特征与其微观结构的复杂性密切相关.孔结构是混凝土微观结构研究的重要内容之一，与混凝土的力学性能紧密相关.研究高地温干热环境下混凝土孔结构对分析其性能的劣化机理及探索改善措施具有重要意义.

本文选取100 ℃高地温干热环境为研究背景，利用恒温烘箱模拟干热环境，对混凝土进行养护.采用隧道常用喷射混凝土配合比，通过力学性能试验和孔结构测试技术研究高地温干热环境下不同纤维混凝土的力学性能和孔隙结构的经时变化特征，分析纤维的改善效果，探索改善机理，并建立强度与孔隙结构参数的数学模型.

1 试验方案

1.1 原料及工况设计

本文拟设计4种工况：①未掺加任何纤维；②掺加体积分数为0.2%的玻璃纤维；③掺加体积分数为1%的端钩型钢纤维；④掺加体积分数为1%的镀铜微丝钢纤维.各工况混凝土采用隧道工程中常用的C25强度等级，参照文献[15]进行基准配合比设计，减水剂质量为胶凝材料质量的1%.各工况的配合比及现场实测坍落度见表1.

表1 各工况及配合比 kg/m3

水泥采用P.O42.5R型普通硅酸盐水泥；细骨料为Ⅱ区河砂，细度模数为2.9；粗骨料采用5～10 mm连续粒级的碎石；减水剂为减水率34%的YH-A聚羧酸高性能减水剂；速凝剂采用JX-E3型低碱液体速凝剂，总碱质量分数为3.5%，初凝时间为150 s，终凝时间为470 s，质量分数为5%；玻璃纤维单丝直径为5～100 μm，长度为10～40 mm，断裂强度大于等于450 MPa；端钩型钢纤维直径为 0.75 mm，长度为30 mm，抗拉强度为1 100 MPa；镀铜微丝钢纤维直径为0.2 mm，长度为13 mm，抗拉强度为2.8 GPa.

1.2 试验方法

本文着重考察高地温环境下不同纤维材料对混凝土性能的影响.考虑到喷射混凝土试件成型需要专门的喷射设备，制作费时、费力且费用高昂，故前期试验可采用模筑混凝土试件替代[16].浇筑成型方式是将混凝土拌和物浇筑到钢制三连模中，采用振动台振动成型.

基于表1中的配合比，每个工况下每个龄期成型2组边长为100 mm的立方体试件.每组共计3个试件，一组用于抗压强度试验，另一组用于劈裂抗拉强度试验.试件于自然环境(温度为20 ℃，湿度为70%)中成型，成型后立即置于温度100 ℃、湿度低于35%的密闭烘箱中，模拟干热环境进行养护.待试件养护1 d后，取出进行拆模，然后将拆模后的试件放回恒温烘箱继续养护.养护至1、7、28 d龄期，达到规定龄期后，从烘箱中取出试件，进行力学性能试验和孔结构测试.

力学性能试验包括抗压强度测试和劈裂抗拉强度测试.孔结构测试采用压汞测试法(MIP)，试验仪器为AutoPore Ⅳ 9500型全自动压汞测孔仪，其测孔范围为3.0～3.6×104nm.测孔前需用尖锤将劈裂后的试件敲成5 mm左右的颗粒状试样，试样中不含石子和粗大纤维.

2 力学性能

为便于比较，图1给出了混凝土抗压强度σc和劈裂抗拉强度σst的折线图.由图可知，100 ℃干热环境下，掺加钢纤维和玻璃纤维后混凝土的抗压强度和劈裂抗拉强度均明显提高.

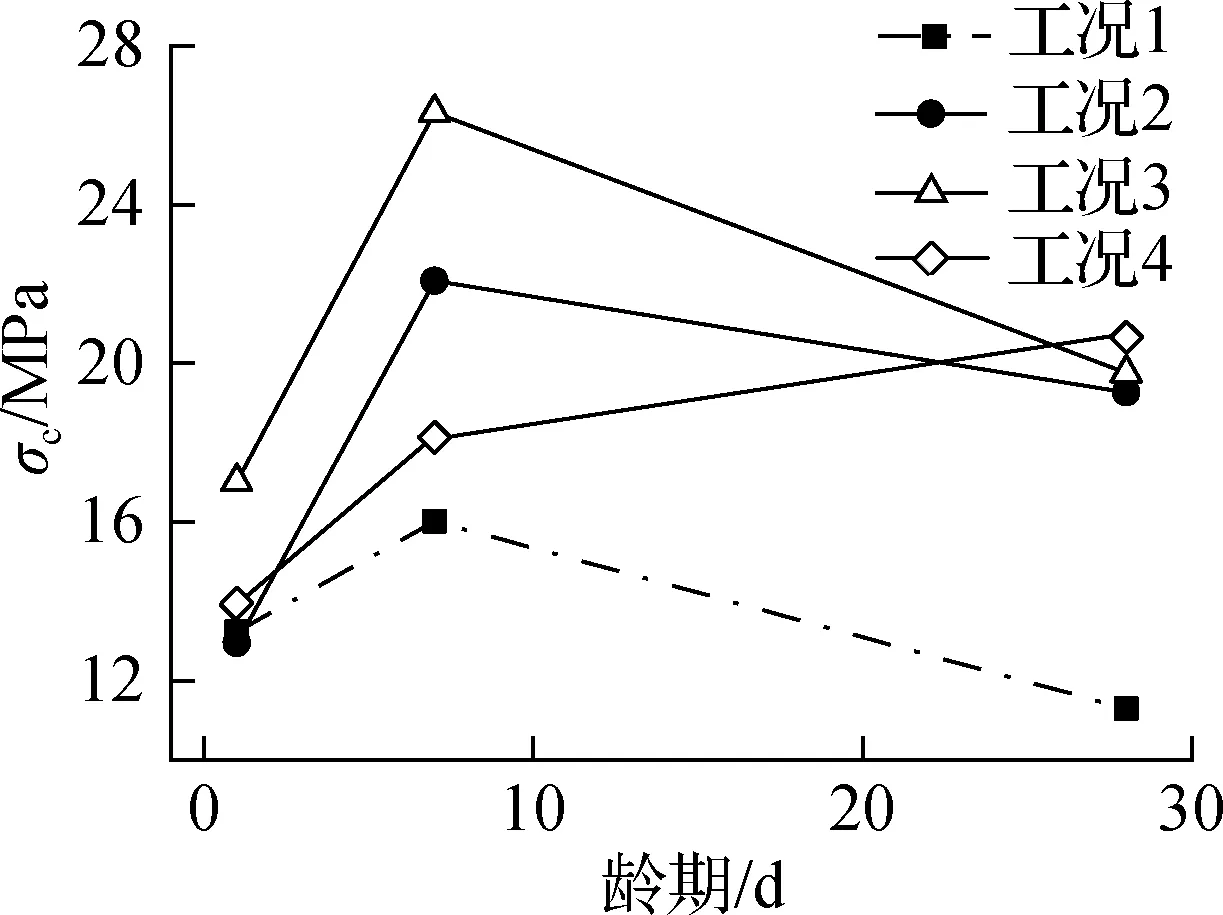
(a) 抗压强度

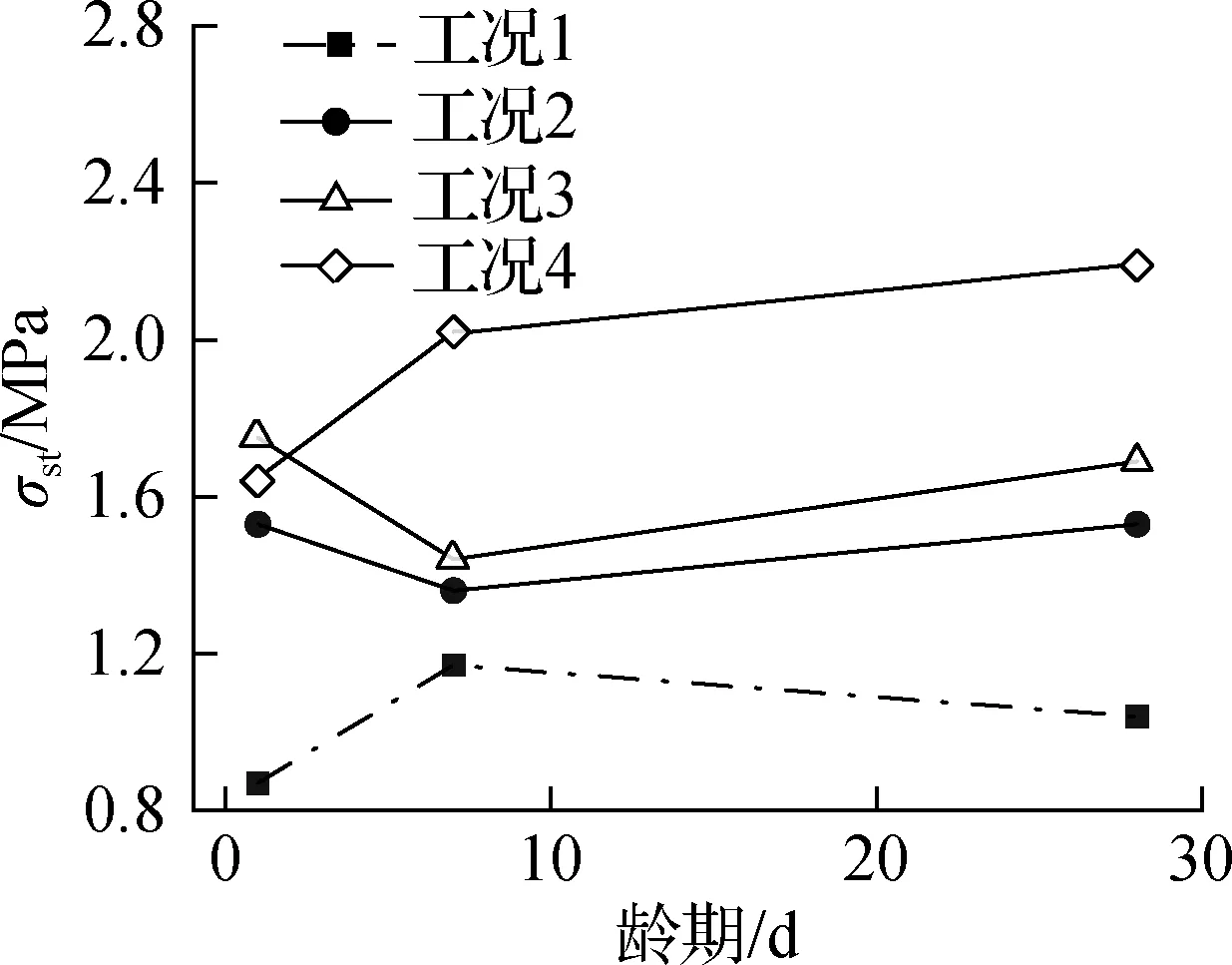
(b) 劈裂抗拉强度

由图1(a)可知，镀铜微丝钢纤维对混凝土抗压强度的改善效果最明显.与工况1相比，工况4下1、7、28 d龄期混凝土的抗压强度分别提高约28.47%、64.40%、74.78%.工况2和工况4下，7 d龄期之前的抗压强度随着龄期的增长逐渐增加，但在7 d龄期之后则逐渐下降.工况3下混凝土的抗压强度在整个养护龄期中均呈单调增长趋势，28 d龄期时抗压强度达到20.65 MPa，相比同龄期工况1的抗压强度提高约82.74%.

由图1(b)可知，端钩型钢纤维对劈裂抗拉强度的改善效果最明显，镀铜微丝钢纤维次之.与工况1相比，工况3下1、7、28 d龄期混凝土的抗拉强度分别提高约88.5%、72.6%、110.6%.工况3下混凝土的劈裂抗拉强度在整个养护龄期中均呈单调增长趋势，且在7、28 d龄期时达到4种工况下的最大值.工况2和工况4下混凝土的劈裂强度在1 d龄期时劈裂抗拉强度较高，之后略有降低，7 d后又开始逐渐回升.究其原因在于，干热环境对混凝土初始水化的促进效果显著，水化速度快，纤维和水泥基迅速黏结，故2种工况下1 d龄期时均表现出较高的劈裂抗拉强度；随着时间的推移，混凝土内水分大量散失，水化速度减缓，干缩增大，水泥基和纤维之间的黏结性能劣化，故龄期为1～7 d时混凝土劈裂抗拉强度随着龄期增长略有降低；7 d龄期之后，干缩逐渐趋于稳定，此时仍有水化产物不断生成，使得纤维和水泥基界面的黏结性能逐渐提升，因此混凝土劈裂抗拉强度在7～28 d龄期时表现为随着龄期增长而略有提高.

综上可知，干热环境下混凝土后期强度随龄期增长而逐渐降低.掺加钢纤维后，因钢纤维的导热系数较大，混凝土内部温场能快速达到均匀，同时钢纤维抑制收缩变形，阻止或阻滞原有裂缝的开展，显著提高了混凝土的抗压强度和劈裂抗拉强度.总体上，较早龄期时，掺加镀铜微丝钢纤维对于混凝土抗压强度的改善效果最为显著；28 d龄期时，掺加端钩型钢纤维对于混凝土抗压强度的改善效果最为显著.

3 孔结构分析

3.1 特征参数

混凝土试件养护至规定龄期后，对直径为5～8 mm、质量为3.5～4.5 g的混凝土试块进行压汞测试.孔隙结构按孔径大小可以分为如下4类：孔径小于10 nm的凝胶孔、孔径为10～100 nm的过渡孔、孔径为100～1 000 nm的毛细孔和孔径大于1 000 nm的大孔.不同工况下的中值孔径、平均孔径及总孔隙率见图2.

由图2(a)和(b)可以看出，掺加纤维材料后，除了1 d龄期的工况2以外，其余龄期及各工况下的中值孔径和平均孔径均小于工况1，特别是28 d时表现尤为突出.

由图2(c)可知，1 d龄期时，工况4和工况2的总孔隙率比工况1分别提升4.3%和16.53%，而工况3则降低了14.70%.随着龄期的增长，工况1和工况3的总孔隙率呈上升趋势，工况2和工况4呈下降趋势.

各工况下不同孔隙结构的孔隙率分布见表2.

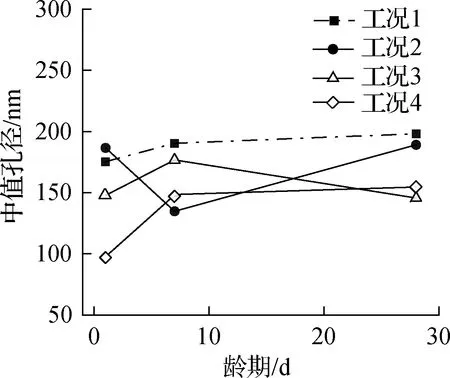
(a) 中值孔径

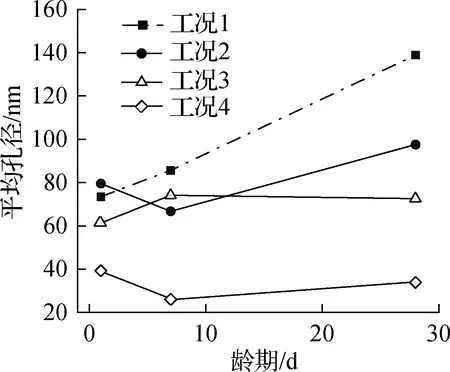
(b) 平均孔径

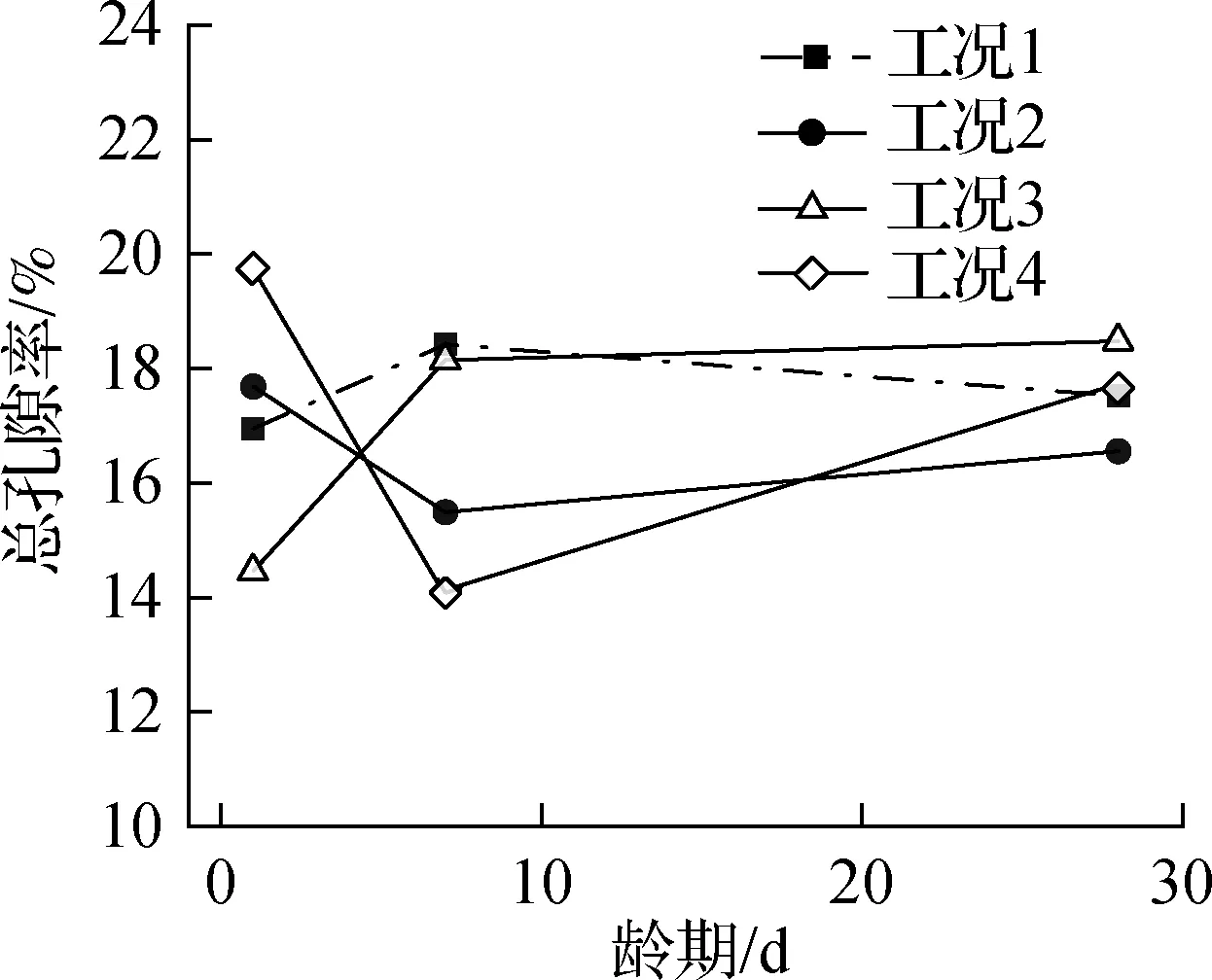
(c) 总孔隙率

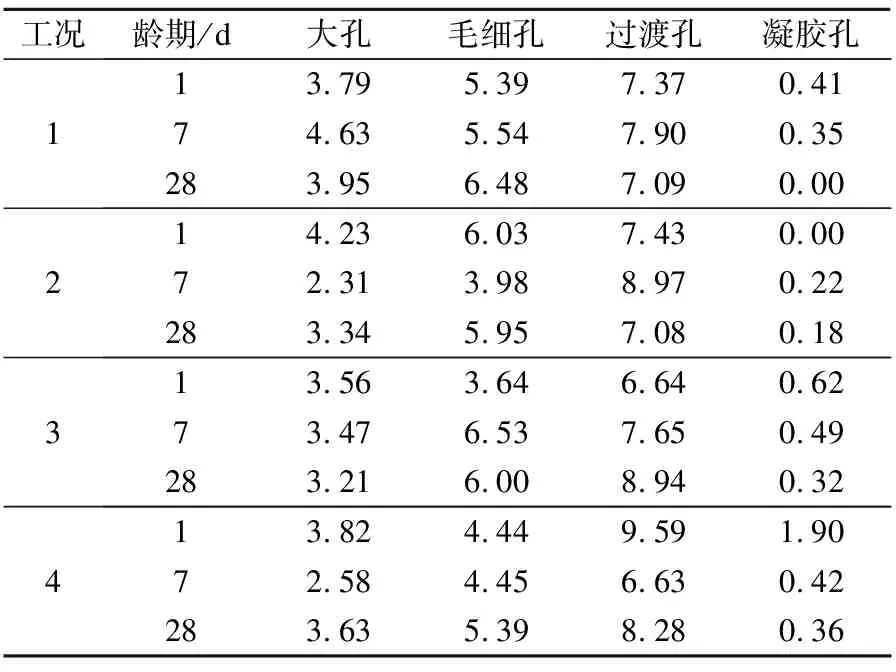
表2 各工况下不同孔隙结构的孔隙率 %

由表可知，7 d龄期时，工况1的总孔隙率最大，其次为工况2和工况3.在7 d龄期后，随着高地温干热环境水分的蒸发，混凝土干缩较大，各工况下混凝土的总孔隙率均呈不同程度的上升趋势.28 d龄期时，工况1的总孔隙率达到17.52%，较工况2高 5.82%，但较工况3和工况4分别低35.43%和 0.78%.究其原因在于，钢纤维的掺入增加了混凝土与纤维之间的界面，从而增大了总孔隙率.

随着龄期的增长，干热环境中混凝土内部水分不断散失，水泥水化不充分以及干缩裂缝的产生导致工况1下孔径大于100 nm的孔隙数量迅速增加，孔隙结构进一步劣化.纤维材料可以有效抑制混凝土内部微裂纹的产生和发展，细化粗大孔隙结构，减少孔径大于100 nm的有害孔孔隙率.28 d龄期时，工况1下的有害孔隙率不断上升，高达 10.43%，而掺加纤维的工况2、工况3和工况4下有害孔隙率分别为9.30%、9.21%和9.02%，较工况1分别降低了10.9%、11.72%和13.55%.

不同工况下孔径分布微分曲线见图3.由图可知，各微分曲线均存在一个峰值，该峰值对应的孔径即为最可几孔径，即出现几率最大的孔径.龄期为1、7 d时各工况下混凝土的最可几孔径接近，均为62.5 nm左右.28 d龄期时工况1的最可几孔径约为110 nm，表明混凝土内毛细孔所占比例较大；其余工况下的最可几孔径仍为62.5 nm左右，说明混凝土中过渡孔所占比例最高.

3.2 分形模型

混凝土作为一种典型的多孔材料，其孔形、孔面积及孔体积等均有明显的分形特征[17].目前，基于压汞法和光学法的分形模型应用较为广泛，前者主要包括空间填充模型、Menger 海绵模型、孔轴线分形模型和基于热力学的分形模型[18].本文采用基于热力学的分形模型对试验结果进行分析，基于压汞测试过程中汞液面表面能增加值与外力对汞所做功相等的原理进行求解[7].

利用压汞法测定数据，对应的分形维数可按照下式计算：

(1)

式中，pi、Vi分别为第i次进汞操作的压力和进汞量；Vn为压力间隔1～n时的累计进汞量；rn为第n次进汞时的孔径；C为系数；Dt为基于热力学关系计算得到的分形维数.

对工况1下7 d龄期的压汞法测定数据进行处理，得到基于热力学关系的对数散点图(见图4).由图可知，对数散点图在整个孔径范围内呈明显的线性关系，孔隙结构分形特征显著，其余工况也具有相同的规律.

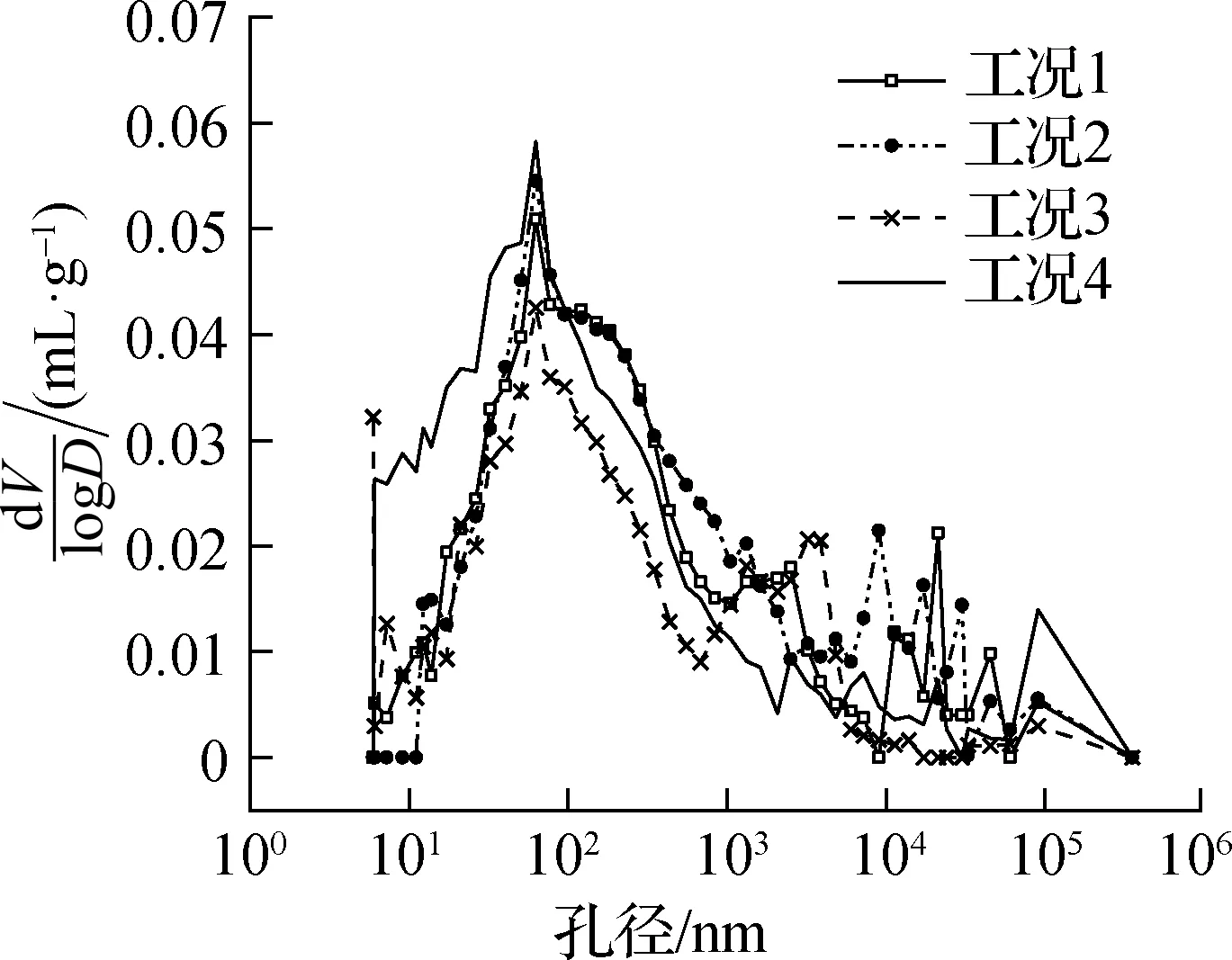
(a) 1 d龄期

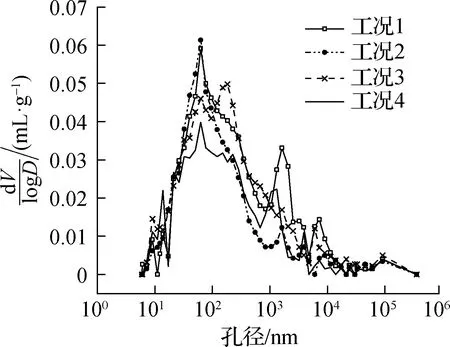
(b) 7 d龄期

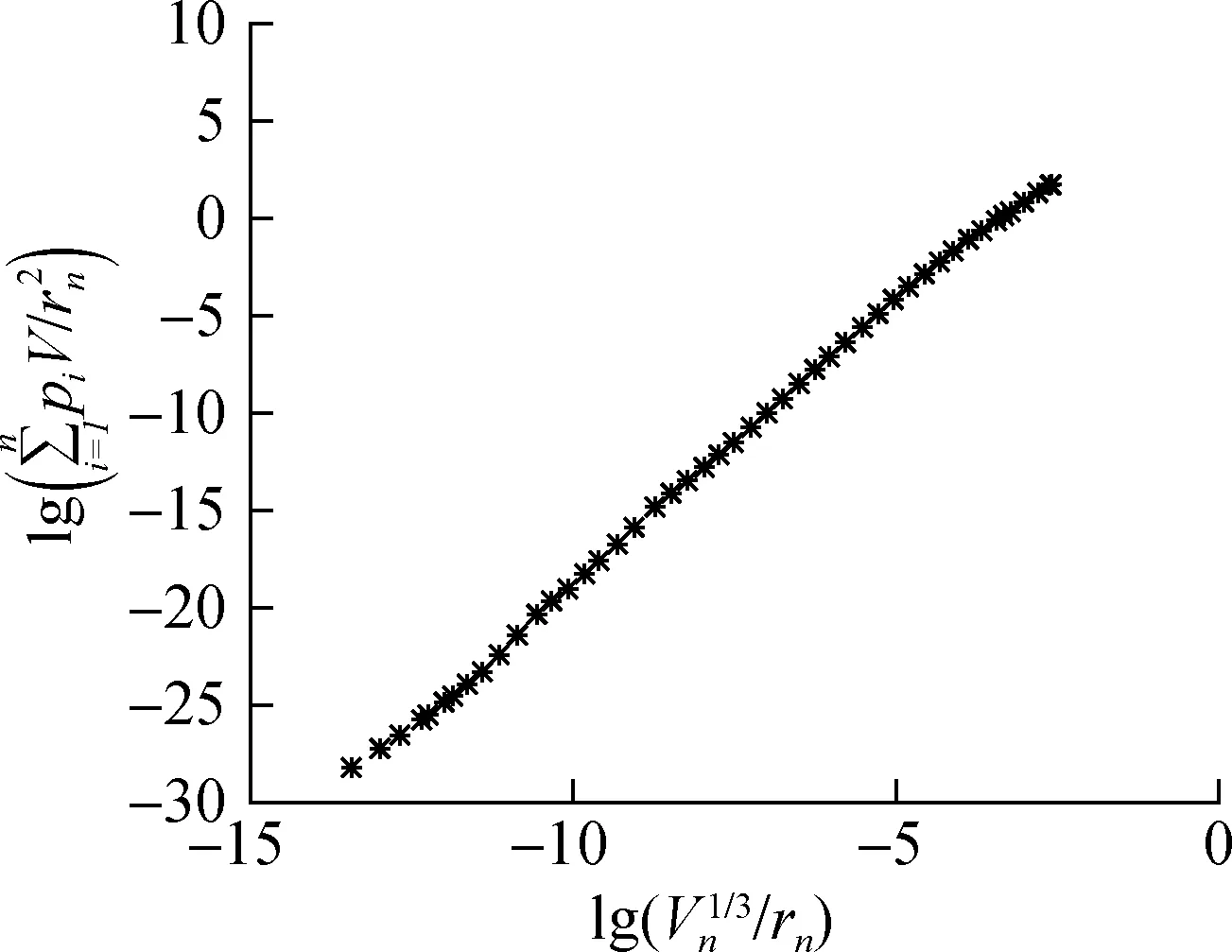
图4 基于热力学关系的对数散点图

由此可知，基于热力学关系的分形模型在整个孔径范围内具有统一的分形维数，且分形特征显著，说明基于热力学关系得到的分形维数可以较好地描述测试范围内的孔径分布情况.各工况下混凝土孔隙结构的分形维数计算结果见表3.

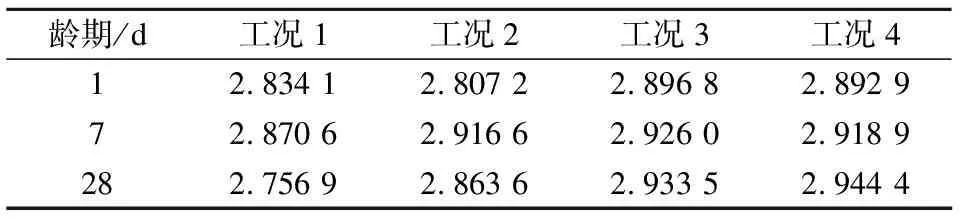
表3 各工况下孔隙结构的分形维数

3.3 混凝土强度与孔隙结构关系

混凝土强度是其宏观性能的最基本指标，研究表明混凝土强度与其孔隙结构存在着密不可分的关系.为定量分析混凝土强度与孔隙结构的关系，学者们进行了大量研究，并建立了相应的数学模型[19-20].干热环境中喷射用混凝土的孔隙率、孔径分布及孔隙形状特征与标准养护条件下差异较大，混凝土强度也相差甚远.因此，干热环境中喷射用混凝土孔隙结构与强度的关系和以往研究结论有所不同.为更好地探求孔隙结构与强度的关系，本节拟通过对力学性能与孔隙结构参数进行多元回归分析，确定干热环境中喷射用混凝土孔隙结构特征与抗压强度、劈裂抗拉强度之间的关系，并建立相应的数学模型.

在回归分析中，同时考虑孔径分布D和孔隙量V对混凝土强度Rc的影响，构建关系模型为

Rc=f(V，D)

(2)

计算可得混凝土抗压强度与中值孔径、平均孔径、分形维数的相关系数分别为-0.150 81、-0.317 23、0.787 18；劈裂抗拉强度与中值孔径、平均孔径、分形维数的相关系数分别为 -0.470 86、-0.719 29、0.667 60.由此说明，混凝土的抗压强度和劈裂抗拉强度与分形维数具有较为显著的相关性，可较好地反映孔径分布情况.因此，选择分形维数作为孔径分布状态的代表参数.

混凝土抗压强度与总孔隙、大孔孔隙、毛细孔孔隙、过渡孔孔隙、凝胶孔孔隙的相关系数分别为-0.133 6、-0.548 1、-0.005 9、0.175 7和 -0.074 4；劈裂抗拉强度与总孔隙、大孔孔隙、毛细孔孔隙、过渡孔孔隙、凝胶孔孔隙的相关系数分别为-0.222 6、-0.356 9、-0.322 3、0.068 4和0.201 80.由此可知，无论是抗压强度还是劈裂抗拉强度，均与总孔隙率及各级孔隙率无显著的相关性.因此，不能采用总孔隙率或某一级孔隙率单独表征混凝土的抗压强度和劈裂抗拉强度，还需考虑孔径分布的影响.

综合考虑各级孔隙率对混凝土抗压强度的影响，将复合孔隙率Pc作为孔隙量的代表参数，计算式可表示为

Pc=α1P1+α2P2+α3P3+α4P4

(3)

式中，P1～P4分别为大孔、毛细孔、过渡孔和凝胶孔的孔隙率；α1～α4分别大孔、毛细孔、过渡孔、凝胶孔孔隙率的强度影响系数.

通过回归分析得到干热环境中喷射用混凝土各级孔隙率的抗压强度和劈裂抗拉强度影响系数，结果见表4.为更好地探索混凝土强度与孔隙结构参数的关系，同时考虑分形维数和复合孔隙率对强度的影响，提出了如下的多因素强度模型：

(4)

式中，σ为混凝土强度；β1～β3为回归系数.

表4 各级孔隙率的强度影响系数

根据式(4)，通过多元回归可得干热环境中喷射用混凝土抗压强度和劈裂抗拉强度与孔隙结构参数间的关系，得出关系模型表达式为

(5)

(6)

回归结果表明，抗压强度和劈裂抗拉强度与孔隙结构参数的多因素关系模型拟合度均大于0.9，且显著性水平小于0.05，说明回归效果显著.因此，所建立的强度模型与试验结果吻合良好，说明该模型可以比较准确地反映干热环境中喷射用混凝土的抗压强度和劈裂抗拉强度与孔隙结构参数间的定量关系.

4 结论

1)干热环境下掺加纤维材料可使混凝土的抗压强度和劈裂抗拉强度明显提高，且端钩型钢纤维的改善效果最好，其次是镀铜微丝钢纤维，最后是玻璃纤维.

2)除1 d龄期外，基准工况下各龄期的中值孔径与平均孔径均高于其余工况，特别是28 d时表现得更加明显.随着龄期的增长，干热环境下基准工况混凝土孔径大于100 nm的有害孔隙数量不断增加，孔结构劣化.掺加纤维材料可有效减少有害孔孔隙率，且钢纤维对孔结构的优化效果优于玻璃纤维.

3)龄期为1、7 d时，各工况下混凝土的最可几孔径接近，均为62.5 nm左右.龄期为28 d时，基准工况的最可几孔径约为110 nm，说明混凝土内毛细孔所占比例较多，而其余工况下的最可几孔径仍为62.5 nm左右.

4)基于热力学关系的分形模型在整个孔径范围内具有统一的分形维数，且分形特征显著.该模型适用于求解干热环境中混凝土的分形维数.

5)干热环境下喷射用混凝土的抗压强度和劈裂抗拉强度与孔隙结构参数的关系模型回归效果显著.该数学模型结果与试验结果吻合良好，可以准确地描述强度与孔隙结构参数的定量关系.