考虑粗骨料破碎的混凝土力学特性细观模拟

崔 溦 魏 杰 李国栋

(1天津大学水利工程仿真与安全国家重点实验室， 天津 300350)(2天津大学中国地震局地震工程综合模拟与城乡抗震韧性重点实验室， 天津 300350)(3中国电建市政建设集团有限公司， 天津 300384)

混凝土具有原材料丰富、抗水性好、抗压强度高、成本低等优点，被广泛应用于土木、水利、桥梁等建筑工程中，是当代应用最广泛的人工建筑材料之一[1].在细观层次上，混凝土被视为由砂浆、粗骨料及二者之间的界面过渡区(ITZ)组成的三相复合材料.粗骨料的体积占混凝土试件总体积的 40%～50%，对混凝土的弹性模量、密度等起着决定性的作用[2].试验证明，粒径越大、形态细长和扁平的粗骨料所占比例越大，则水分越容易在粗骨料表面聚集，从而造成 ITZ 的强度减弱，即粗骨料的形状和强度会间接影响混凝土试件的力学特性[3].现有混凝土力学特性研究中，为了简化模型，将粗骨料视为刚性材料进行数值模拟[4]，然而对混凝土试件进行单轴压缩试验发现，存在粗骨料破碎和主裂缝穿过粗骨料延伸扩展的现象.因此，研究粗骨料破碎对混凝土力学性能的影响具有重要意义.

Wriggers等[5]使用有限元法对混凝土进行建模,基于蒙特卡洛方法随机生成粒径、尺寸、位置不同的球形粗骨料，通过塑性损伤本构关系预测裂缝的扩展，研究表明裂缝首先发生在骨料周围，然后在砂浆内传播.周正峰等[6]采用黏聚力单元模型模拟混凝土中裂缝的萌生和扩展，结果表明，混凝土强度随ITZ强度的增加而增加.近年来，鉴于离散元方法在模拟裂缝的便捷性，学者们使用离散元方法(DEM)对混凝土进行中尺度建模[7-8].Nitka等[9]采用不同力学性能的球形黏结颗粒模拟砂浆和骨料，而裂缝则由黏结键破坏表示.目前，关于颗粒破碎的研究大多集中在堆石料、钙质砂、铁路道砟等方面[10]，混凝土研究则涉及较少，粗骨料破碎对混凝土力学特性的影响有待进一步研究.关于颗粒破碎的模拟方法主要有连续-离散耦合法(Combined FDEM)和离散元法(DEM)[11]，且基于离散元的颗粒破碎法具有计算效率高、能考虑颗粒的复杂形状等优点[12].

本文基于离散元软件 EDEM，建立了粗骨料-砂浆-ITZ的三相混凝土离散元模型.采用黏结颗粒模型(BPM)建立粗骨料破碎模型，以模拟粗骨料和砂浆之间的力学特性，从细观层次探究粗骨料破碎对混凝土变形和破坏特性的影响.

1 数值模型

本文将混凝土视为砂浆、粗骨料和ITZ组成的三相复合材料，将ITZ建模为砂浆和骨料颗粒之间的弱界面，其实现方式为均匀削弱骨料黏结力或删除部分黏结键[13].考虑骨料与骨料、骨料与砂浆、砂浆与砂浆之间的黏结特性，采用三维扫描技术对粗骨料进行扫描，并重建其三维几何数字模型.基于黏结颗粒模型(BPM)，模拟粗骨料与砂浆之间的力学行为，建立混凝土三相离散元模型.

1.1 BPM模型

BPM模型能实现颗粒之间的黏结与颗粒破碎模拟.在BPM模型中，黏结键将小颗粒单元黏结成为大块的物料模型[14].在外力作用下小颗粒单元间的黏结键破碎，从而模拟物料破碎、产生裂缝的效果，适用于模拟岩石破碎、混凝土产生裂缝等脆性材料破坏的过程.

BPM模型黏结计算示意图见图1.图中，R1和R′1分别为颗粒1的物理半径和黏结半径；R2和R′2分别为颗粒2的物理半径和黏结半径.由于黏结半径等于或略大于颗粒半径，因此生成黏结键的两颗粒可能没有发生真正接触.在生成黏结键的瞬间，颗粒的合力和合力矩会重置为0，计算每一时间步长下合力和合力矩的变化值，计算公式为

(1)

式中，ΔFn、ΔFt分别为法向和切向力变化值；ΔMn、ΔMt分别为法向和切向力矩变化值；vn、vt分别为法向和切向速度；ωn、ωt分别为法向和切向角速度；Kn、Kt分别为法向和切向刚度；Δt为计算时间步长；S为黏结区域面积；J为黏结区域横截面的极惯性矩.对于球形颗粒单元，有

(2)

(3)

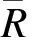
图1 BPM模型黏结计算示意图

BPM模型中的黏结区域为圆盘形状，其外围的最大拉应力σmax和最大剪应力τmax分别为

(4)

(5)

式中，Fn、Ft分别为法向力和切向力；Mn和Mt分别为法向力矩和切向力矩.

当σmax大于抗拉强度或τmax大于抗剪强度时，颗粒间的黏结键断裂.黏结键断裂后，对应的力、力矩、刚度等不再作用于颗粒单元.

1.2 黏结颗粒BPM模型的参数标定

ITZ是指骨料和砂浆之间宽度为15～30 μm的低强度、高孔隙率的薄层.为简化处理，参考文献[9,13]的方法，将ITZ建模为骨料和水泥砂浆颗粒之间的薄弱接触，此时ITZ不存在物理宽度.骨料与骨料、骨料与砂浆以及砂浆与砂浆之间的接触均采用BPM模型模拟.

选用强度为C30的混凝土，尺寸为 150 mm×150 mm×150 mm.利用PLS-500T型微机控制电液伺服加载试验机对混凝土试件进行单轴压缩试验，压板的加载速率为1 mm/min.将加载板位移除以试件初始长度可得轴向应变，最终得到混凝土单轴压缩的应力-应变曲线.在EDEM软件中建立混凝土的BPM模型(见图2).砂浆颗粒的半径为3.5 mm，随机生成的粗骨料颗粒粒径范围为10～31.5 mm.将粗骨料三维模型导入EDEM软件后，软件将粗骨料颗粒默认为刚体，在外荷载的作用下无法变形和破坏，因此将粗骨料作为不可破碎的刚体.

图2 混凝土单轴压缩离散元模型

BPM模型中包含如下3类参数：① 材料的本征参数，如密度、剪切模量、泊松比等；② 接触参数，如碰撞恢复系数、静摩擦系数、滚动摩擦系数等；③ 黏结参数，如单位面积的法向刚度、单位面积的切向刚度、临界法向力、临界切向力、黏结半径等.C30混凝土中的材料为砂浆和粗骨料；模拟混凝土的单轴压缩试验时，压板和底板为钢材.因此，需要确定砂浆、粗骨料、钢材的本征参数及三者之间的基本接触参数.此外，还需对砂浆颗粒与砂浆颗粒、砂浆颗粒与粗骨料颗粒间的黏结参数进行参数标定.

本征参数是材料自身的特性参数，参考文献[7，15]，砂浆的泊松比为0.2，密度为2 000 kg/m3，剪切模量为0.56 GPa，弹性模量为1.3 GPa；粗骨料的泊松比为0.3，密度为2 630 kg/m3，剪切模量为0.72 GPa，弹性模量为5.3 GPa；钢材的泊松比为0.3，密度为7 800 kg/m3，剪切模量为0.92 GPa，弹性模量为6.5 GPa.

基本接触参数可由室内试验或者现场试验测得.文献[16]利用室内试验对混凝土的基本接触参数进行了研究，本文选取的接触参数见表1.

表1 接触参数

黏结参数与颗粒粒径、粗骨料形状、混凝土配合比等有关，且对混凝土的宏观力学性能存在较大影响，需要对其进行标定.参数标定时，对C30混凝土试件进行单轴压缩试验，并在EDEM软件中模拟，不断更改黏结参数，直至数值模拟得到的应力-应变曲线与试验结果相符.

标定过程中初始单位面积的法向刚度kn和单位面积的切向刚度kt分别为

(6)

(7)

式中，E、ν分别为材料的弹性模量和泊松比.

在kn和kt的基础上，反复修改黏结参数，直到符合混凝土宏观力学特性，结果见表2.

表2 混凝土的黏结参数

图3给出了室内试验和数值模拟得到的应力-应变曲线对比图.由图可知，试验结果和模拟结果的曲线变化趋势相似.在加载初期，室内试验曲线和数值模拟曲线呈现非线性变化.随着加载的进行，混凝土进入线弹性阶段，曲线均近似线性变化，直至达到比例极限.随后，混凝土开始软化，应力-应变曲线开始弯曲，且随着加载的进行，曲线的弯曲程度不断增加.当模拟值和试验值分别达到峰值应力fc和f′c时，曲线开始迅速下降.当应力值达到收敛值时，混凝土完全破坏.

表3给出了室内试验和数值模拟的混凝土强度指标对比.由表可知，抗压强度、抗拉强度、抗折强度的误差都在10%以内，说明数值模拟的准确性较高.图4为混凝土最终破坏形态的对比图.由图可知，在外荷载的作用下，试件底部和顶部生成细小裂缝；随着荷载的不断增大，裂缝延伸扩展，最终造成混凝土试件的破坏.数值模拟得到的最终破坏形态与实际单轴压缩试验结果相似性较好.

图3 混凝土单轴压缩试验的应力-应变曲线对比图

表3 室内试验和数值模拟的强度指标对比 MPa

(a) 室内试验

(b) 数值模拟

1.3 颗粒破碎BPM模型的参数标定

离散元模拟颗粒破碎的方法包括基于BPM模型的颗粒破碎方法和碎片置换法(FRM)[11]. 本文采用基于BPM模型的颗粒破碎方法模拟粗骨料破碎，其原理是通过黏结键将小颗粒黏结成的团聚体替代原始颗粒(即母颗粒).当黏结键承受的剪切力或者法向力超过极限值时，黏结键断裂，颗粒也会随之破碎.

选择4种代表性形状的碎石作为粗骨料，编号分别为Ⅰ～Ⅳ，其产地为天津，母岩为花岗岩，粒径为10.0～31.5 mm.为反映混凝土粗骨料的三维结构特征，采用三维扫描技术对粗骨料进行扫描并重建其三维几何数字模型.为使仿真模拟效果更接近于实际情况，粗骨料用非球形颗粒表示，在EDEM软件中构建相应的BPM模型，结果见图5.

(a) 颗粒Ⅰ

(b) 颗粒Ⅱ

(c) 颗粒Ⅲ

(d) 颗粒Ⅳ

计算并对比真实颗粒和离散元模型颗粒形状参数，包括球度s、凸度Cx、主尺度(长轴长度a、中轴长度b和短轴长度c)等.球度S用于衡量颗粒与球体的接近程度，定义为等同球体的表面积与颗粒表面积的比值；凸度反映了三维颗粒的紧凑程度.球度和凸度的表达式分别为

(8)

(9)

式中，V为颗粒体积；As为颗粒表面积；VCH为凸包的体积.

表4给出了颗粒Ⅰ的形状参数对比.由表可知，三维模型对粗骨料的还原性较高，离散元模型能反映出粗骨料的形状特性.

表4 颗粒Ⅰ的形状参数对比

利用WDW-300型电子式万能材料试验机对颗粒Ⅰ进行单轴压缩试验，加载速度设置为2 mm/min.粗骨料参数标定结果见表5.

基于标定参数得到的力-位移曲线见图6.由图可知，力-位移曲线中包含多个峰值点.随着加载的进行，在达到每个峰值点后力均会急剧下降，表示颗粒发生一次破碎.对比数值模拟和室内试验中第1次发生破碎时的力和位移，其误差分别为3.1%和7.6%，故可认为表5中的黏结参数能够反映出粗骨料真实的力学性质.

表5 粗骨料的黏结参数

图6 颗粒Ⅰ在单轴压缩试验下的力-位移曲线

图7对比了颗粒Ⅰ在室内试验和数值模拟中的最终破坏模式.由图可知，无论是室内试验还是数值模拟中，颗粒Ⅰ均发生了剪切破坏.裂缝从粗骨料中部萌生并向四周扩展，直至贯穿于整个粗骨料，从而造成粗骨料的破碎，说明数值模拟得到的破坏模式与试验结果吻合较好.

(a) 室内试验

(b) 数值模拟

2 骨料破碎对混凝土力学特性的影响

为使数值模型更接近于实际试验，将部分粗骨料设置为可破碎状态，探究可破碎粗骨料的质量分数w对混凝土试件的应力-应变曲线、抗压强度及最终破坏模式的影响.受计算效率限制，且实际混凝土受压过程中只有部分粗骨料发生破坏，故将w设置为0%～40%.为减少可破碎骨料随机分布对模拟结果的影响，每个工况下进行3组试验，将结果取平均值.w=10%时的混凝土模型见图8.

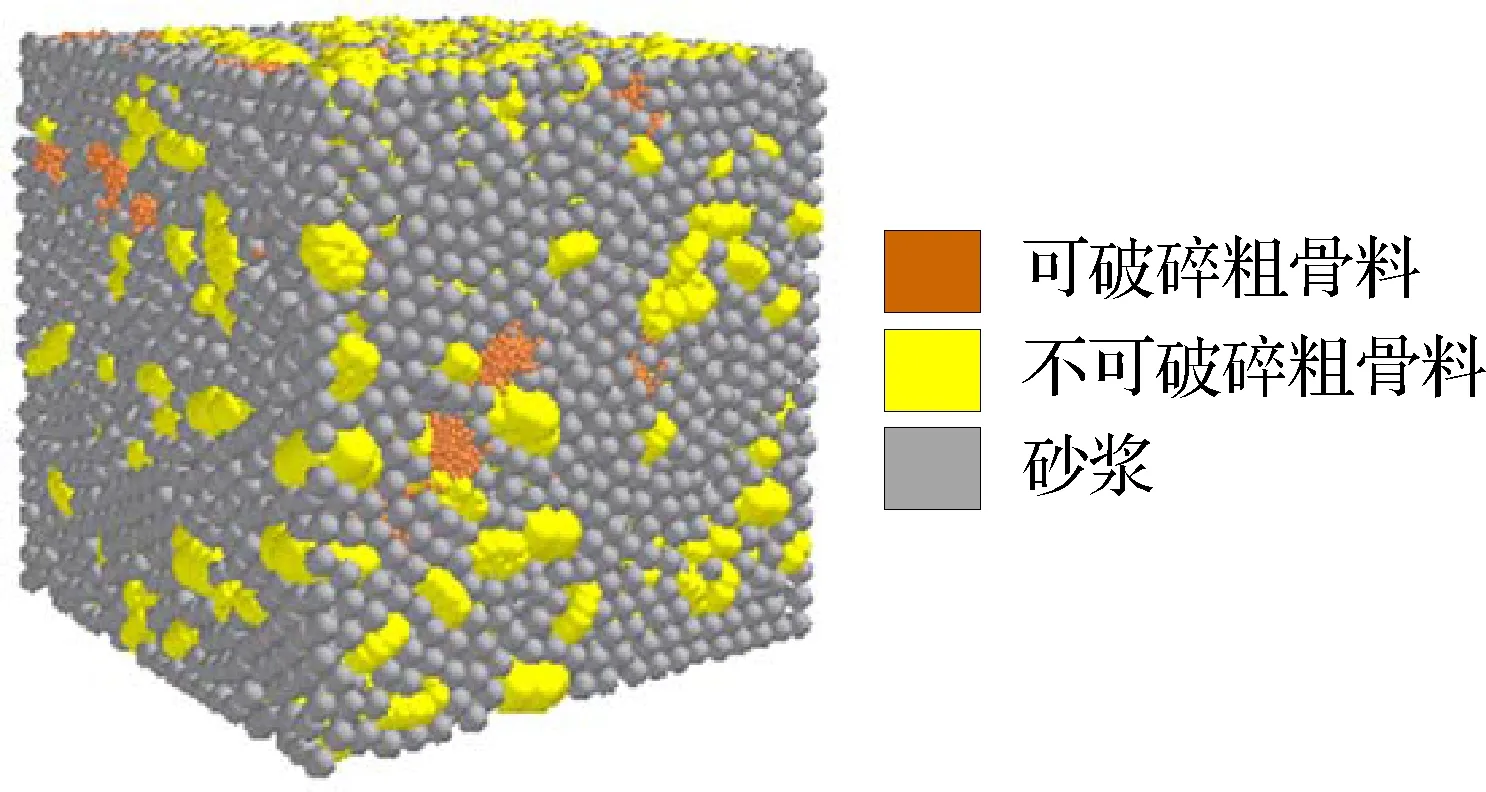
图8 混凝土模型(w=10%)

2.1 应力-应变曲线

图9为含不同可破碎粗骨料质量分数的混凝土的应力-应变曲线.由图可知，当混凝土试件中的w=0%时，混凝土试件的峰值应力fc= 33.17 MPa，对应的峰值应变εc=1.98×10-3.不同可破碎粗骨料质量分数下的混凝土应力-应变曲线形状相似，变化趋势基本相同.粗骨料的破碎会影响混凝土的峰值应力和应变.当0%5%时峰值应力和应变随w的增加逐渐减小.

图9 不同可破碎粗骨料质量分数混凝土应力-应变曲线

综上可知，粗骨料破碎对混凝土的变形特性存在显著影响.粗骨料的破碎会增强混凝土的硬化特性和延性，改变峰值应力和应变，且峰值应力和峰值应变整体上随可破碎粗骨料质量分数的增加而减少.

2.2 抗压强度

混凝土的抗压强度受粗骨料粒径、水灰比、水泥级配等多种因素影响，是混凝土结构最重要的力学特性之一[17].图10为可破碎粗骨料质量分数对抗压强度的影响曲线.由图可知，随着混凝土中可破碎粗骨料质量分数的增大，抗压强度先增大后减小，最后趋于稳定.

图10 粗骨料破碎对抗压强度的影响

图10中的曲线可分为3个阶段：① 当w<3%时，混凝土的抗压强度随w的增大而略微增加.w=0%时混凝土的抗压强度为33.17 MPa；w=3%时，混凝土的抗压强度达到最大值35.23 MPa.产生这一现象的原因在于，采用离散元方法模拟混凝土时，离散元颗粒间会存在一定的孔隙，w较小时粗骨料破碎产生的颗粒会对孔隙进行填充，从而增加了混凝土试件的密实性，使混凝土的抗压强度增大.②混凝土抗压强度随w的增大而减小，w=5%时的抗压强度为33.24 MPa，与w=0%时基本一致.随着w的增加，混凝土抗压强度迅速下降，可破碎粗骨料对裂缝的阻碍作用减弱，导致混凝土更易破坏.当5%

2.4 破坏模式

单轴压缩试验过程中，混凝土内部局部区域出现应力集中并萌生裂缝，在外荷载的作用下裂缝会继续扩展，其扩展方向与外荷载方向基本平行.当裂缝扩展到一定程度后，裂缝之间相互贯穿形成主裂缝.主裂缝决定了混凝土试件的破坏形式.图11给出了考虑和不考虑粗骨料破碎时混凝土试件的破坏模式.由图可知，不考虑粗骨料破碎时，裂缝沿着粗骨料颗粒与砂浆颗粒的交界面延伸扩展，粗骨料没有破碎.对于可破碎粗骨料质量分数为15%的混凝土试件，部分粗骨料发生破碎且存在主裂缝穿过粗骨料的现象，位于主裂缝位置上的可破碎粗骨料破碎最为严重，其他位置损伤程度较小.

图12给出了混凝土破坏前后的黏结键.试件破坏后，断裂黏结键个数为24 108.断裂黏结键显示了混凝土中裂缝的延伸趋势和易破碎位置，主裂缝贯穿整个试件，这与图12中的破坏模式吻合较好.

(a) w=0%

(b) w=15%

(a) 破坏前

(b) 破坏后

3 结论

1) 采用三维扫描技术构建了粗骨料三维几何模型.通过BPM建立了粗骨料破碎模型，以模拟粗骨料和砂浆之间的力学特性，进而实现了考虑粗骨料破碎的混凝土粗骨料-砂浆-ITZ的三相离散元模型.

2) 含不同可破碎粗骨料质量分数的混凝土的应力-应变曲线形状相似，发展趋势相同.峰值应力和应变整体上随可破碎粗骨料质量分数的增加而减少.

3) 粗骨料的破碎会影响混凝土的抗压强度.当w<3%时，少量粗骨料破碎产生的颗粒会填充于离散元模型中颗粒间的孔隙中，增加密实性，混凝土抗压强度出现短暂的上升；随着w的增加，混凝土更易产生裂缝，抗压强度迅速下降.当w达到临界值32%后，抗压强度几乎不变.

4) 从细观角度解释了裂缝不仅沿着ITZ拓展，还存在着贯穿粗骨料的现象.