基于多尺度和注意力机制的滚动轴承故障诊断

丁 雪 邓艾东 李 晶,3 邓敏强 徐 硕 史曜炜

(1东南大学能源与环境学院， 南京 210096)(2东南大学火电机组振动国家工程研究中心， 南京 210096)(3南京审计大学信息工程学院， 南京 211815)

滚动轴承作为风电机组传动链系统的关键部件，在运行过程中极易受到力、热及振动等非线性、非平稳因素的影响[1]，从而产生变形、裂纹、断裂等损伤，进而严重影响风电机组的运行[2].因此，对滚动轴承进行精确的故障诊断不仅可以降低维修成本，而且可以提高风电机组的可靠性和稳定性，具有重要的现实意义.

近年来，卷积神经网络(CNN)作为深度学习的重要分支之一，已逐渐成为故障诊断领域的研究热点.李恒等[3]将短时傅里叶变换后的二维时频谱图作为CNN的输入，提高了模型的鲁棒性.陈仁祥等[4]应用离散小波变换构造原始信号的时频矩阵并送入CNN网络进行分类，以验证所提方法的可行性.曲建岭等[5]将原始振动信号直接作为一维卷积神经网络的输入，依靠模型自身的结构对原始信号进行特征提取和故障分类.

虽然上述文献均表明CNN网络在滚动轴承故障诊断中的可行性，但仍然存在以下问题：传统的CNN网络都采用单一尺度卷积核提取特征值，无法捕获振动信号的多尺度特征；当前提出的模型绝大多数仅将获得的特征简单堆叠后进行故障诊断，并未考虑多尺度特征在故障诊断中的不同权重影响.

针对上述问题，本文提出了一种多尺度注意力卷积神经网络(MSACNN)模型.该模型通过多尺度层对不同尺度特征的信息进行融合，然后引入注意力机制使模型更加关注于具有判别力的特征，从而提高模型的特征学习能力，最后通过全连接层的多分类函数实现滚动轴承的故障诊断.实验结果表明，本文模型不仅在同负载各测试集上达到很高的准确率，而且在变负载工况下具有较强的迁移泛化能力和鲁棒性；同时，该模型在强噪声环境下也具有良好的诊断性能.

1 原理

1.1 CNN基本网络结构

卷积层由多个卷积核组成，卷积层利用卷积核对输入数据的局部区域执行卷积运算，并通过激活函数生成输出特征图[6]，卷积的运算过程如下：

(1)

池化层通过池化核对卷积层的输出进行降采样操作，在保留原有主要特征的基础上实现了降维减参[7]，同时使网络结构不易出现过拟合.最常用的池化层是最大池化层，其数学表达式为

(2)

式中，ah(m,t)为第h层中第m个特征图的第t个神经元的激活值；g为池化区域的宽度；n为第n个池化核；ph(m,n)为相应池化层的输出.

1.2 注意力机制

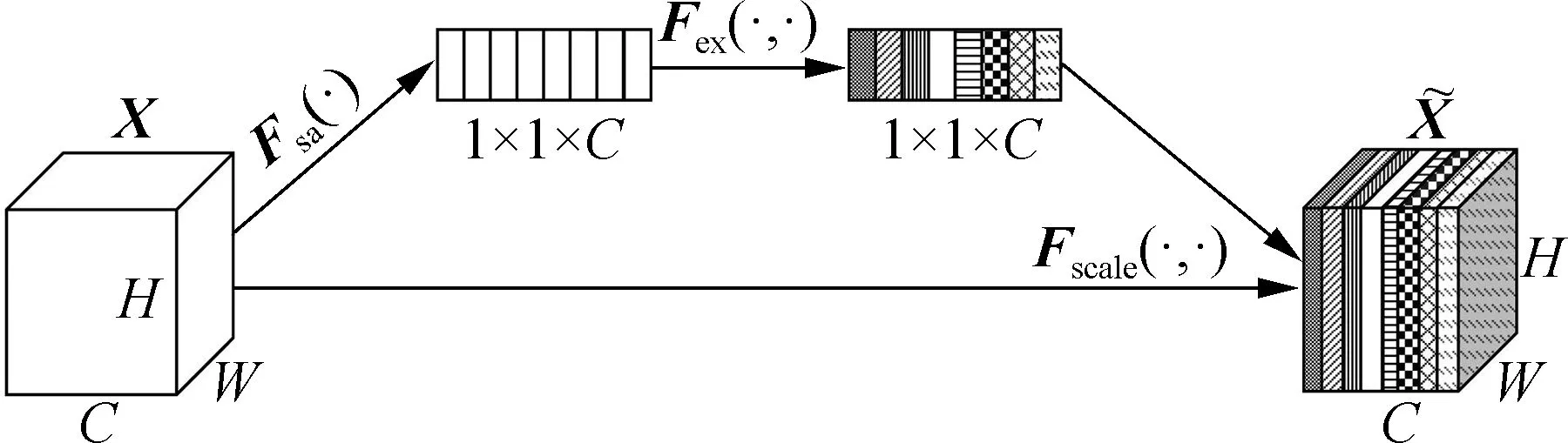
图1 注意力机制示意图

SE模块的工作过程分为3个步骤：压缩、激发和乘积.首先是压缩操作，沿着特征通道的方向将H×W×C维的特征图通过全局平均池化操作压缩为1×1×C的向量，其中每个通道的二维特征图压缩成一个具有全局感受野的通道特征响应值.其计算过程如下：

(3)

式中，uc(v,w)为v×w通道的二维矩阵；v=1,2,…,H；w=1,2,…,W；c为压缩通道的第c个元素；zc为压缩操作后的输出.

其次是激发操作，使用2个全连接层和一个sigmoid激活函数来参数化门控机制.全连接层用于更好地融合全部的输入特征信息，而sigmoid函数用于将输入特征映射为0～1之间的归一化权重，其具体实现过程如下：

sc=σ(W2δ(W1zc))

(4)

式中，σ为sigmoid函数；δ为Relu激活函数；W1、W2为2个全连接层的权重；sc为激发操作后的输出.

最后是乘积操作，经过上述操作得到的通道权重利用乘法逐通道加权到原来的特征上，从而在通道维度上实现对原始特征的重新分配.计算公式如下：

(5)

2 MSACNN模型结构

2.1 模型结构

本文在多尺度和注意力机制的基础上构建了如图2所示的网络模型结构：该模型主要由2个卷积-卷积-最大池化对、一个多尺度特征提取层、一个注意力机制融合层、一个全局平均池化层和2个全连接层组成.2个卷积-卷积-最大池化对借鉴了VGGNet的卷积神经网络结构，连接在其之后的是多尺度特征提取层，该层由卷积核大小分别为3、5的卷积层和用于降维减参、卷积核大小为1的PW(PointWise)卷积层构成.通过将这2对卷积层进行拼接，拓宽了网络的宽度并提取到了丰富的多尺度特征.为获得更高维度的特征信息，使模型的注意力集中在更具判别性的特征上，将上述得到的多尺度特征引入到注意力模块，对更重要的特征赋予更多的权重，接着进入全局平均池化层，以进一步减少参数并防止过拟合.最后通过2个全连接层和Softmax分类器输出故障分类的诊断结果.

图2 MSACNN模型结构

2.2 模型参数

MSACNN模型在卷积过程中大部分采用3×3的卷积核，这是因为较小的卷积核能够保证在具有相同感知野的情况下，提升网络深度，保证网络精度，从而在一定程度上提升模型的效果.在训练过程中，迭代次数设置为80，批次大小设置为32，将学习速率为0.001的Adam优化器用于更新网络参数，该模型的其他参数在表1中列出.

3 实验分析

3.1 CWRU轴承故障数据集

采用美国凯斯西储大学(CWRU)轴承故障数据集对本文方法的有效性进行验证.

3.1.1 数据集

CWRU滚动轴承试验台如图3所示，该试验台由1.5 kW的电动机(左侧)、转矩传感器(中间)和功率计(右侧)组成.以驱动端轴承SKF6205作为研究对象，系统采样频率为12 kHz.轴承故障由电火花技术单点引入，分为内圈故障、滚动体故障和外圈故障3种故障类型，每种故障类型包含3种故障尺寸：0.177 8、0.355 6和0.533 4 mm，因此可将轴承状态分为9种故障状态和1种正常状态，共10种轴承状态.分别在0、0.735、1.471、2.206 kW四种不同负载下采集轴承振动以用于实验.

表1 MSACNN模型参数

图3 CWRU滚动轴承试验台

为避免数据样本过少而导致的过拟合问题，本文采用重叠采样的方式进行数据增强，如图4所示.从原始振动信号的起始点开始采集，每次采集 2 500 个点，采集完成后则向后移动200个数据点继续采集，每种故障状态采集500个样本.其中，300个样本作为训练集，100个样本作为验证集，其余100个样本作为测试集，故每种负载下总共 5 000 个样本，具体的实验数据情况如表2所示.为验证MSACNN模型的有效性，创建了数据集A、B、C、D、E，具体情况如表3所示.

图4 数据重叠采样示意图

表2 实验数据描述

表3 所创建数据集的描述

3.1.2 数据集重构

表2所示的数据集为原始振动数据的一维时间序列形式.为充分利用卷积神经网络在图像分类中的优势，便于卷积和池化等操作，本文将一维信号转换为二维图像以用作模型的输入.一维原始数据[2 500，1]重构为二维特征图形式[50，50，1]，其中1表示1通道.重构方法示意图如图5所示，具体过程为：首先等长截取长度为2 500的一维时间序列样本，截取50段，每段含50个数据点，然后将该50段数据进行堆叠以获得一个50×50的二维特征图，因此每类轴承状态均有500个格式为[50，50，1]的输入特征图样本数据[7].

图5 输入数据格式重构

3.2 同负载下故障诊断结果及与其他方法的比较

为更好地分析所提模型的诊断性能，本文分别使用创建的数据集A～E进行实验，并将该模型与相关文献中一些模型在数据集A～E下的分类准确率进行了比较，如基于集成经验模态分解(EEMD)的支持向量机诊断模型[9]、基于稀疏滤波无监督特征学习模型[10]、基于时域振动信号的多层感知器(MLP)模型(Time+MLP)[11]、基于小波包能量(WPE)和深度卷积网络的能量波动多尺度特征挖掘模型(WPE+CNN)[12]、基于数据驱动的多头注意力卷积神经网络智能故障诊断模型Multihead CNN[13]和基于一维卷积神经网络的故障诊断模型1D-CNN[14].不同模型对不同数据集的故障诊断准确率如表4所示.

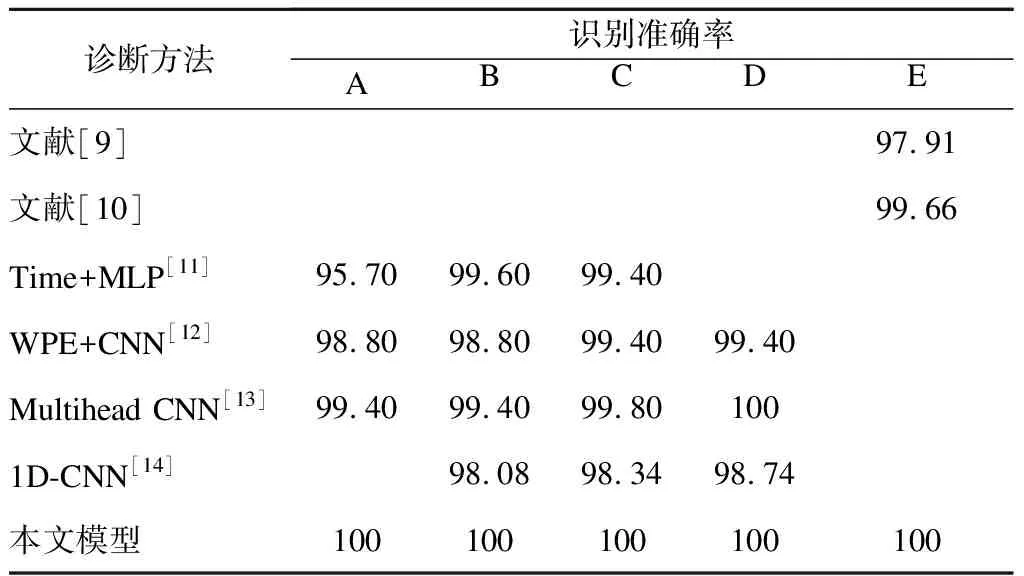
表4 不同模型对5个数据集的故障识别准确率 %

如表4所示，在同负载(训练集、验证集和测试集均为同一负载数据)的情况下，本文提出的模型在无需提取任何特征的情况下，在数据集E上的故障诊断准确率达到100%，明显高于文献[9]，原因主要在于该类模型的学习效果对所提取特征的依赖性较强，然而人工提取的特征适应性较差，因此在混有多种负载的数据集E上表现较差，这也突出了深度学习自动提取特征的优势.与其他深度学习方法[10-14]相比，本文模型的故障识别准确率也优于其他方法，在数据集A～E上的识别准确率均可达到100%.其原因在于多尺度分析方法和注意力机制相结合的二维卷积神经网络能够挖掘数据的内在联系，自动提取抽象特征，并可对特征实现权重分配，从而达到更高的诊断精度.

3.3 抗噪性能分析

工业系统中滚动轴承的振动信号具有高度的复杂性和强烈的环境噪声，因此在不同噪声信号的影响下对轴承的故障进行准确诊断尤为重要.评价信号噪声强弱的标准是信噪比(SNR),为模拟实际工业系统中的噪声环境，可在原始振动信号中加入具有不同信噪比的高斯白噪声以形成含噪声的复合信号.SNR计算公式如下：

(6)

式中，Psignal为信号的能量；Pnoise为噪声的能量.

为验证本文所提模型的抗噪性能，与带有训练干扰的卷积神经网络(TICNN)[15]、基于宽内核的卷积神经网络(WDCNN)[16]、WDCNN(with adaBN)[16]、基于多尺度粗粒度层的卷积神经网络(MSAFCN)[17]等模型进行对比.在内圈故障的原始振动信号上加入信噪比为-4～10 dB范围的高斯白噪声，实验结果如图6所示.

图6 本文模型和4种模型在不同噪声环境下的性能

显然，本文模型优于其他4种CNN模型，在信噪比范围为-4～10 dB时，其平均诊断准确率超过99.8%.总体而言，5种模型的精度随着信噪比的增加而提高，当信噪比超过2 dB后，精度的变化趋于稳定.这是因为在噪声较小的情况下，诊断精度主要取决于模型本身提取故障特征的能力.当信噪比从0 dB到10 dB变化时，只有本文模型始终保持在100%的识别准确率，表明该算法具有较高的故障特征提取能力.当信噪比降至-4 dB时，本文模型仍能达到98.90%的识别准确率，分别比TICNN、WDCNN、WDCNN(with adaBN) 和MSAFCN高16.85%、31.95%、6.25%、14.13%.实验结果表明，本文模型在没有任何去噪预处理的情况下，仍可保持很强的抗噪声能力，具有较好的鲁棒性.

3.4 跨不同负载域的轴承诊断结果与分析

为验证本文模型在负载变化时故障诊断的迁移通用能力，模型训练和测试所用的数据均来自不同负载.例如，B-C表示在数据集B上训练样本，在数据集C上进行测试，每个方法实验10次以最大程度减少随机性.本文将在数据集B上进行训练，在数据集C、D上分别进行测试；然后再在数据集C上进行训练，在数据集B、D上进行测试，最后将实验结果与基于快速傅立叶变换的多层感知器(FFT-MLP)模型、1D-CNN[14]模型、基于改进多尺度和注意力的卷积网络(IMS-FACNN)[18]模型和WDCNN[16]进行对比，结果如图7所示.

图7 不同模型的负载适应性测试结果比较

由图7可看出，FFT-MLP在域适应方面表现最差，平均准确率为81.38%，相比之下，本文模型具有更高的准确率，平均准确率为97.20%，这也表明本文所提模型从原始信号中学习的特征比传统的频率特征更具有域不变性.对于1D-CNN和IMS-FACNN这2种深度卷积模型而言，其每个域适应实验的准确率均明显低于本文模型.WDCNN虽然从数据集B到C的准确率略高于本文模型，但是当从数据集B到D、C到B和C到D进行自适应时，本文模型的分类精度均高于WDCNN，域适应的稳定性较强.

3.5 特征可视化

卷积神经网络的黑匣子特性使得理解其内在的学习机制变得尤为困难.因此，为理解本文模型的内部操作过程，将对模型输出的(多尺度层前、多尺度层后、注意力机制后和全连接层后)特征图进行可视化，此外，还将对上述输出的特征通过t-SNE(t-distributed stochastic neighbor embedding)算法降为二维并进行可视化.

3.5.1 卷积核输出特征图的可视化

本文抽取训练集中某个故障样本的图片作为模型的输入，并将模型的卷积层1-1、卷积层1-2、最大池化层1-3、卷积层2-1、卷积层2-2、最大池化层2-3和多尺度特征提取层分别进行输出特征图的可视化，可视化结果如图8所示.由图可知，模型的浅层网络提取的是纹理、细节特征，其包含更多的特征，也具备提取关键特征的能力.而随着模型层数的加深，更深层次的网络提取的是轮廓、形状和最强特征，但提取的有效特征越来越少，也越来越抽象，越来越稀疏.

(a) 第1个卷积-卷积-池化对后的特征图

(b) 第2个卷积-卷积-池化对后的特征图

(c) 多尺度特征提取层后的特征图

3.5.2 t-SNE降维可视化

上述中间特征图的可视化较为抽象，下面利用t-SNE降维算法将各层特征降为二维以更直观地表示故障诊断分类过程，其中C1～C10表示轴承状态的10种不同类别.原始振动信号故障特征、信号经过几次卷积池化操作但未进入多尺度层前的输出特征、进入多尺度层然后的输出特征、进入注意力机制模块后的输出特征和进入全连接层后的输出特征这5个t-SNE特征可视化结果如图9所示.

如图9(a)所示，原始振动信号的特征交互重叠，杂乱无章地分布在整个空间中，没有明显的分界线.由图9(b)可知，经过几次卷积池化操作，相同类别特征的点开始逐渐聚集，但不同样本之间仍存在大面积重叠的现象.由图9(c)可知，经过多尺度层的多尺度特征提取作用，不同类别样本之间的故障特征界限开始逐渐清晰，可在一定程度上区分部分样本类别.由图9(d)可知，由于注意力机制对特征的权重分配操作，各类样本特征越来越分散，各种类别已基本被分开.由图9(e)可知，经过全连接层后，类与类之间的距离更大，各样本之间的特征分离度达到最高.综上可知，本文模型可从输入的原始信号中有效提取特征，具备很好的分类性能.

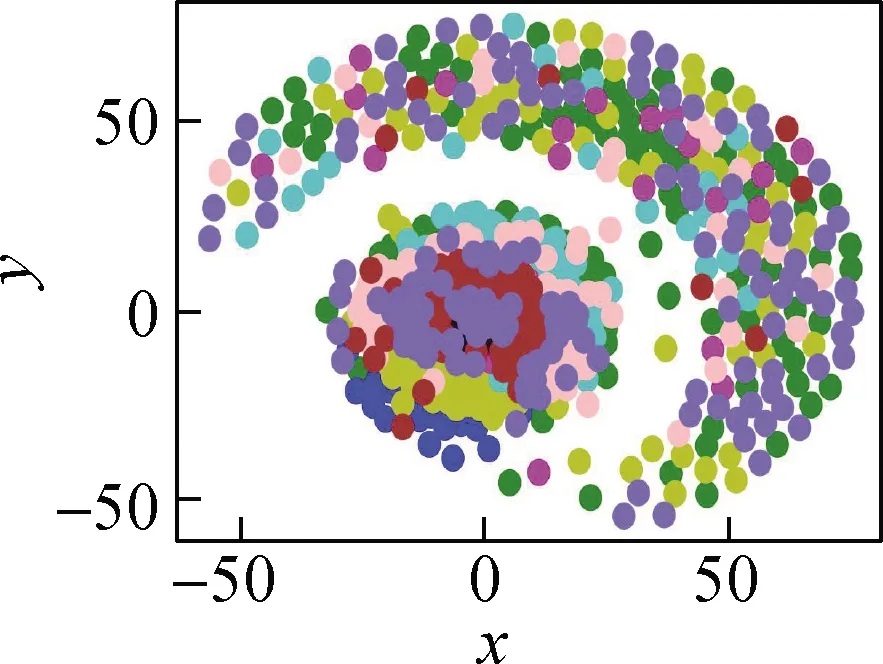
(a) 原始振动信号

(b) 信号进入多尺度层前的特

(c) 信号进入多尺度层后的

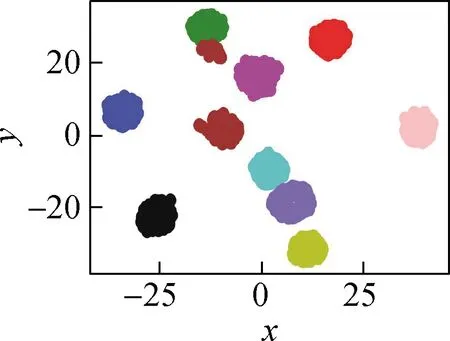
(d) 信号进入注意力层后的特

(e) 信号进入全连接层后的特征图像

4 结论

1)MSACNN模型将一维时间序列转化为二维图像作为模型的输入，并通过大量数据的学习以自适应提取轴承的故障特征，避免了人工提取特征的过程，摆脱了对复杂信号处理技术的依赖，提高了诊断效率.

2)MSACNN模型具有较强的抗噪声干扰能力，在噪声环境下仍然具有良好的故障诊断性能.

3)MSACNN模型不仅能在同负载各测试集上达到很高的准确率，而且对不同负载工况也有较高的准确率，模型在识别精度和诊断鲁棒性方面兼具良好表现.

4)本文模型较复杂，运算成本较大，在后续工作中会继续优化模型，以更好地学习特征表示，在提高诊断性能的同时简化网络结构，最大程度地降低运算成本.