基于多种群差分进化算法的分子动力学模拟体系中局部晶体结构识别

张作恒 周蕾蕾 何思渊 李 艳 马宝财 顾 宁

(1东南大学生物科学与医学工程学院， 南京 210096)(2南京市第一医院医学影像科， 南京 210006)

分子动力学模拟将微观行为与宏观特性联系起来, 是研究晶体合成过程的必要工具.在晶体合成过程中，晶核的形成、生长以及特定条件下晶体的相变，均与局部原子/离子的空间排布直接相关.识别模拟体系中局部结构的动态变化是关键的科学问题.然而，从庞大的模拟数据中准确识别出特定结构的方法却鲜有报道.

目前，常用的局部结构识别算法包括共近邻原子分析法(CNA)[1]与多面体模板匹配法(PTM)[2].这2种算法已被作为程序模块集成在Lammps软件中[3]，能够直接识别出面心立方(fcc)、密排六方(hcp)、体心立方(bcc)等简单晶体结构，但无法直接对刚玉、反尖晶石等较为复杂的晶体类型进行结构分类.复杂体系常用分析方法有2种：① 人工直接观察分析[4]，但由于体系中离子相互遮挡，体系较大时则无法采用该方法；② 基于统计学定义相关结构表征参数[5]，该方法计算简单，但无法进行目标结构的勾画.文献[6]提出了一种基于深度学习的局部结构识别算法，但在实际应用中需针对特定结构训练网络.因此，准确识别排列方式复杂的局部晶体结构，已成为分子动力学模拟中亟待解决的问题.

鉴于此，本文提出了一种基于多种群差分进化算法的分子动力学模拟体系中局部晶体结构的识别算法.该算法以一种晶体结构作为模板，结合模拟体系的几何结构与拓扑结构，定义了用于表示模拟体系的局部区域与模板间重合度的目标函数.然后，利用多种群差分进化算法，搜索出目标函数最大时的平移距离与旋转角度，进而识别出模拟体系的局部区域中所有符合晶体有序排布的原子/离子.最后，采用所提算法对Al、Mg、Fe原子分别构成的3种金属单质聚集体以及4种铁的氧化物、氢氧化物、羟基氧化物进行结构识别.

1 空间变换与目标函数

从模拟体系点集P={p1,p2,…,pN}中识别排列方式符合晶体结构(点集Q={q1,q2,…,qM})原子/离子的过程，可视为结构的相似度比对匹配过程.通过平移与旋转2种空间变换操作，使模拟体系能够最大程度地与晶体结构相重合.

在模拟体系点集P中指定一点po，将模拟体系中每个点pi以向量-po平移，使得点po与三维空间坐标原点重合.同时，po也作为平移后模拟体系的旋转中心，将整个模拟体系按照x、y、z三个方向先后旋转θx、θy、θz，得到变换后的点p′i，即

p′i=RzRyRx(pi-po) 1≤i≤N,po∈P

(1)

在点集P中选择一个与点po所对应原子/离子类型相同的点qo，将晶体点集中每个点qj以向量-qo平移，得到变换后的晶体结构点q′j，此时点qo也与三维空间坐标原点重合，即

q′j=qj-qo1≤j≤M,qo∈Q

(2)

式中，点p′i和点q′j分别构成空间变换后的新点集P′={p′1,p′2,…,p′N}和Q′={q′1,q′2,…,q′M}.

两点集间的几何相似度常以基于欧氏距离的均方根误差表示.定义点集Q′中距离点p′i最近的点为与点p′i相对应的点q′i，即

(3)

定义函数h(p′i,q′i)来判定模拟体系点集P′中的点与晶体结构点集Q′中相对应的点是否重合，即

(4)

式中，δ为阈值参数.

当点p′i与点q′i的偏差值不大于阈值参数δ时，认为模拟体系中点p′i和晶体结构中点q′i基本重合.通过设置阈值参数δ来修正轻微热运动对结构的影响，通常将其设为配位键长的10%～50%.

以晶体结构排布的原子/离子一般集中在局部范围，为了防止模拟体系中其他区域的原子/离子排布对识别结果产生影响，需要将模拟体系中的原子分割为若干子集分别进行比对.根据原子/离子间的拓扑结构判定其所属的局部区域，识别出属于同一区域且与晶体结构点集重合的点.因此，将模拟体系视为无向图G(P′,E)，其顶点集合即为点集P′，边与点集P′和Q′的相似度以及点集P′代表的原子/离子配位情况相关，即E={ei,j|h(p′i,q′i)=1,h(p′j,q′j)=1,且p′i与p′j间存在配位键/共价键}.在确定无向图中的顶点与边的基础上，采用并查集算法[7]分析该无向图的连通性.

点p′o与点q′o分别为点集P′和点集Q′的三维空间坐标原点，即p′o与q′o完全重合，因此仅考虑与点p′o处于同一局部区域的原子/离子排布情况即可.点p′i与点p′o是否存在路径相连通可表示为

(5)

则模拟体系P′中与点p′o处于同一区域且符合晶体结构的原子/离子数量为

(6)

模拟体系中局部区域与晶体结构间重合度的目标函数为

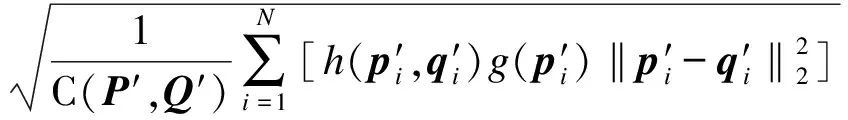
(7)

由此可知，识别到的符合晶体结构排布的原子/离子数越多，相应原子/离子的均方根误差越小，则当前空间变换操作更为合理.

不同晶胞中同一位置的原子/离子具有等效性.为了减少搜索空间，将目标函数中的点qo替换为一个晶胞中与点po所代表的原子/离子类型相同的索引I，则

(8)

2 多种群差分进化算法

选用由Storn等[8]提出的基于种群的差分进化算法，求解式(8).该算法主要包含种群初始化、种群适应度评估、变异操作、交叉操作、选择操作5个部分.

2.1 种群初始化

目标函数中的4个参数可被视为一个四维向量X={I,θx,θy,θz}.其中，I取为[1,m]范围内的整数，m为晶胞中与点po所表示原子/离子类型相同的原子数目；θx,θy,θz取为[0,2π)间的实数.

种群初始化是在整个参数空间中生成NP=1 200个X向量构成的初始种群.初始种群中第t个个体表示为

Xt,0={It,0,θxt,0,θyt,0,θzt,0}t=1,2,…,NP

(9)

It,0=1+mrand(0,1)θxt,0,θyt,0,θzi,0=2πrand(0,1)

式中，随机数生成函数rand(0,1)表示在[0,1)之间生成一个均匀分布的随机数.若I不为整数，则对其向下取整.

2.2 适应度评估

将第G代所有个体依次代入目标函数中，计算目标函数值f(Xt,G)并将其作为适应度.在此之前，需对向量X中的4个参数进行预处理.旋转角度具有周期性，若θx、θy、θz超过[0,2π)的范围，则需按照下式将其映射在[0,2π)的范围：

θ=θ-2kπk∈{…,-2,-1,0,1,2,…}， 0≤θ-2kπ<2π

(10)

采用下式将I映射为[1,m]范围内的整数：

I=I-kmk∈{…,-2,-1,0,1,2,…}， 1≤I-km≤m

(11)

2.3 变异操作

为结合多种变异策略的优势，采用多种群差分进化算法[9].每次迭代更新时，将种群随机划分为3个大小相等的子种群，各子种群采用不同的变异策略.第1个子种群采用DE/rand/1变异策略，即

Vt,G=Xr1,G+F(Xr2,G-Xr3,G)

(12)

第2个子种群采用DE/best/2变异策略，即

Vt,G=Xbest,G+F(Xr1,G-Xr2,G)+F(Xr3,G-Xr4,G)

(13)

第3个子种群采用DE/rand-to-best/1变异策略，即

Vt,G=Xi,G+F(Xbest,G-Xi,G)+F(Xr1,G-Xr2,G)

(14)

式中，Vt,G为第G代变异得到的新个体；Xr1,G、Xr2,G、Xr3,G、Xr4,G为从各子种群中随机选取的4个个体；下标t,r1、r2、r3、r4为向量索引值，且t≠r1≠r2≠r3≠r4；Xbest,G为第G代种群中的最优个体；F为缩放因子，本文中由均值为0.9、标准差为0.2的正态分布产生，被截断在[0.75, 1.25]范围内[10-11].此外，每次迭代结束后，重新对所有个体进行随机分组.

2.4 交叉操作

差分进化算法还引入了交叉操作，即将差分变异后的向量与上一代向量进行交叉，得到新的向量Ut,G.向量第s维度的数值ut,s,G为

(15)

式中，CR为交叉操作参数，本文中由均值为0.5、标准差为0.2的正态分布产生，被截断在[0.1, 0.9]范围内[11]；srand为[1,4]内的随机整数，用于确保交叉操作后的向量中存在元素来自变异向量，避免算法停滞.

2.5 选择操作

DE算法采用贪婪选择策略，即将本次迭代新生成向量的适应度与上一代向量的适应度进行逐一对比.若新生成向量Ut,G拥有更高的适应度，则该向量取代上一代向量进入后续迭代，否则继续保留上一代向量Xt,G，即

(16)

3 实例评估验证

3.1 模拟体系的构建

利用本文算法分别对多种金属单质聚集体和金属化合物聚集体进行识别，以验证所提方法.金属单质聚集体选用fcc结构的Al[12]、hcp结构的Mg[13]和bcc结构的Fe[14]，其原子数分别为2 916、4 860、3 456.由于铁的化合物结构多样，截取铁的氧化物、羟基氧化物、氢氧化物晶体作为金属化合物聚集体，即α-Fe2O3[15]→2 880 Fe3++4 320 O2-，Fe3O4[16]→ 2 000 Fe3++1 000 Fe2++4 000 O2-，α-FeOOH[17]→ 2 496 Fe3++2 496 O2-+2 496 OH-，Fe(OH)2[18]→ 3 024 Fe2++6 048 OH-.

采用Lammps(version 22 Aug 2018)软件包实现模拟[3].体系耦合了恒温恒体积的NVT系综，温度通过Nose-Hoover恒温器控制.模拟体系的盒子尺寸比截断后的晶体块尺寸大4 nm，以确保体系中任何离子都不会受到周期性扩展离子的影响.

对于金属单质模拟体系，选择EAM势作为力场参数[19-21].时间步长设为1 fs.Al、Mg和Fe体系能量最小化后，先分别在1 000、 600、1 050 K高温下进行50 ps的模拟，再在300 K下进行300 ps的模拟.图1给出了弛豫后的金属原子聚集体结构，其初始晶体结构扭曲为多个长程有序区域组成的多晶结构.选择每个区域的中心原子为点po，寻找与该点属于同一区域的局部晶体结构.Al与Mg聚集体阈值参数δ设为0.075 nm，Fe聚集体阈值参数δ设为0.05 nm.

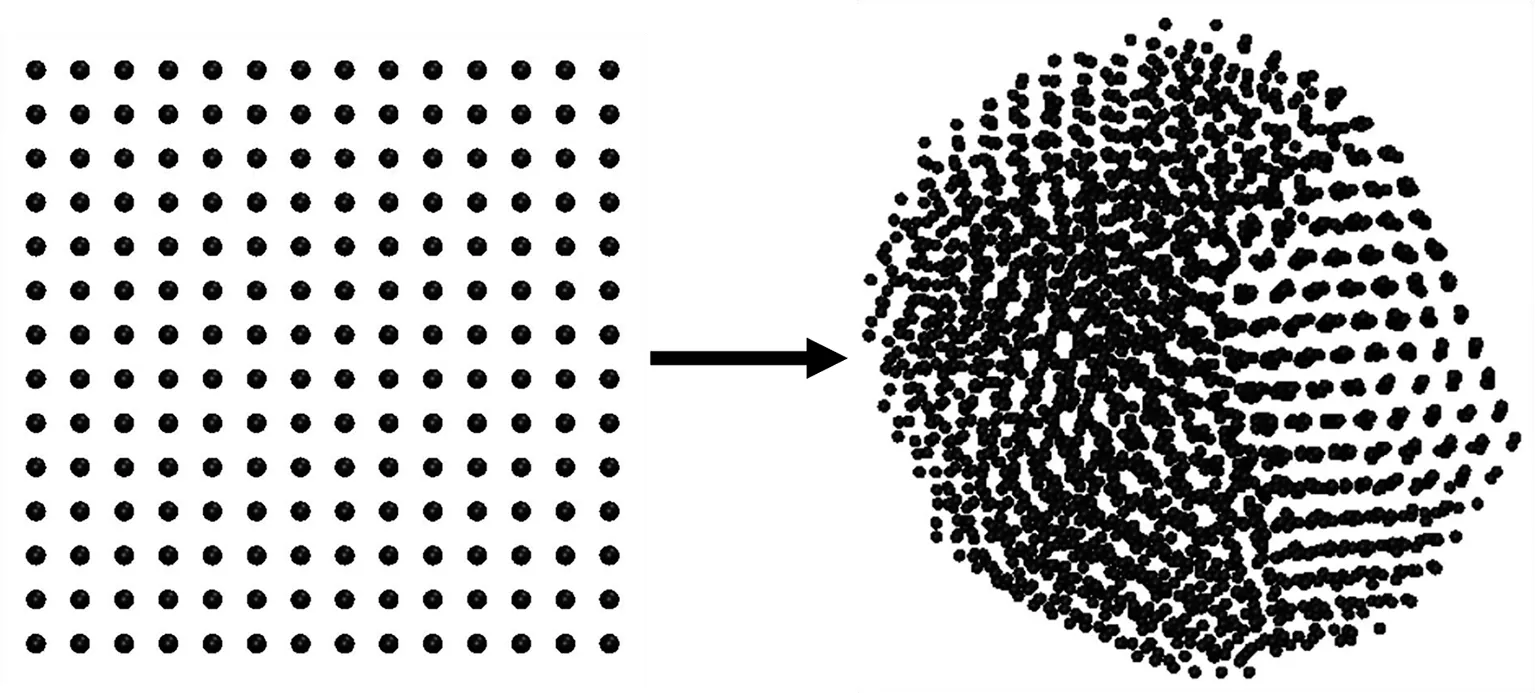
(a) 2 916个Al原子聚集体

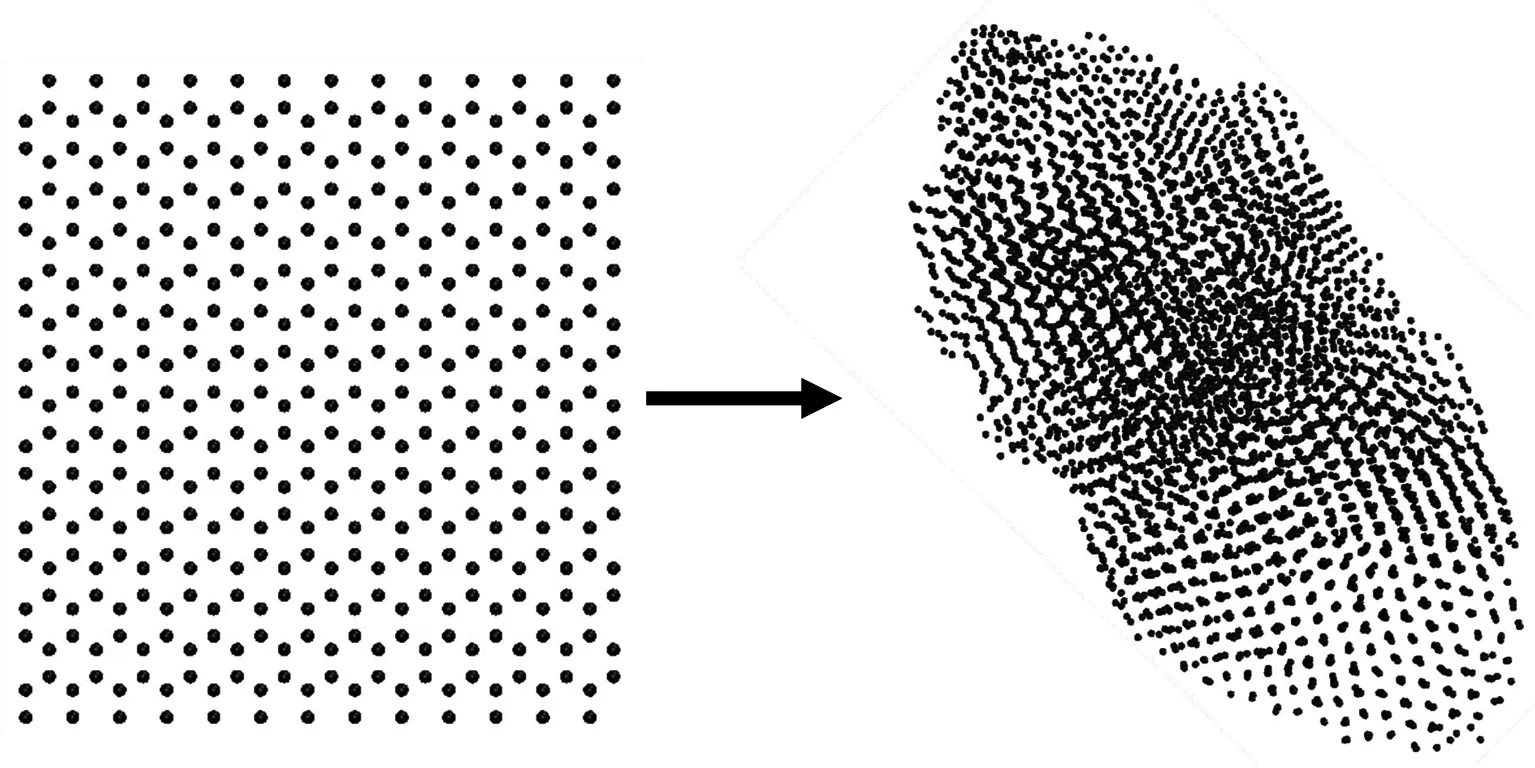
(b) 4 860个Mg原子聚集体

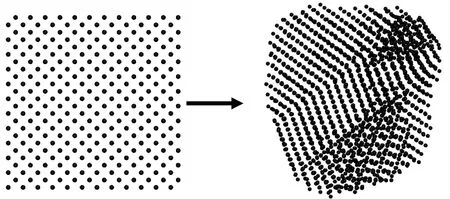
(c) 3 456个Fe原子聚集体

对于铁的化合物模拟体系，选择Coulombic-Buckingham势作为力场参数[22].其中，非化学键相互作用的截断距离设为1.5 nm.时间步长设为0.5 fs.每个离子聚集体能量最小化后，在300 K温度下进行50 ps的模拟，结果见图2.由图可知，弛豫后的离子聚集体表面会因欠配位而产生结构扭曲，但其内部仍存在与晶体类似的有序结构.选择每个聚集体中心的离子为点po，寻找与该点属于同一区域的局部晶体结构.2 880 Fe3++ 4 320 O2-聚集体、2 000 Fe3++ 1 000 Fe2++ 4 000 O2-聚集体与3 024 Fe2++ 6 048 OH-聚集体的阈值参数设为0.05 nm，2 496 Fe3++ 2 496 O2-+ 2 496 OH-聚集体的阈值参数设为0.075 nm.

3.2 结果分析

对Al、Mg、Fe构成的3种金属单质聚集体，分别采用CNA算法、PTM算法以及本文算法进行结构识别，结果见图3.CNA算法中，Al、Mg、Fe聚集体的截断半径分别为0.345 7、0.387 0、0.346 4 nm，PTM算法中阈值均设为0.015 nm.由图可知，3种算法得到的结果基本一致.由于CNA算法与PTM算法均基于原子周围配位情况来判定结构类型，处于聚集体表面或不同取向晶体结构交界处的原子即使呈明显长程有序排布，仍无法被认定为相应晶体结构.本文算法能直接比较聚集体中的原子与给定晶体结构的相似性，因此可识别出更多的边界原子.此外，本文算法还包含了对连通域的计算，可将聚集体直接分割为多个独立的晶体区域.相互独立的晶体区域通过颜色进行区分；在同一区域中，原子的排布方式及取向均相同.

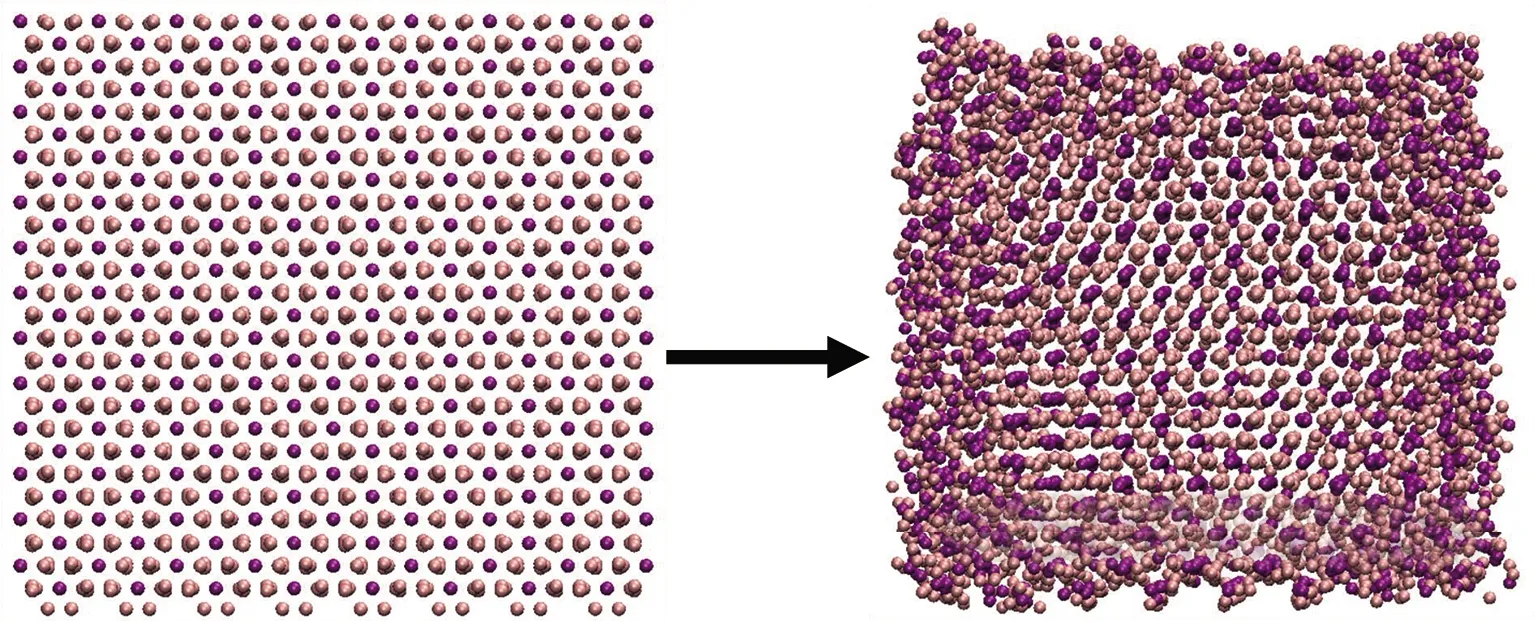
(a) 2 880 Fe3+ + 4 320 O2-聚集体

(b) 2 000 Fe3+ + 1 000 Fe2+ + 4 000 O2-聚集体

(c) 2 496 Fe3+ + 2 496 O2- + 2 496 OH-聚集体

(d) 3 024 Fe2+ + 6048 OH-聚集体

(a) 2 916个Al原子聚集体

(b) 4 860个Mg原子聚集体

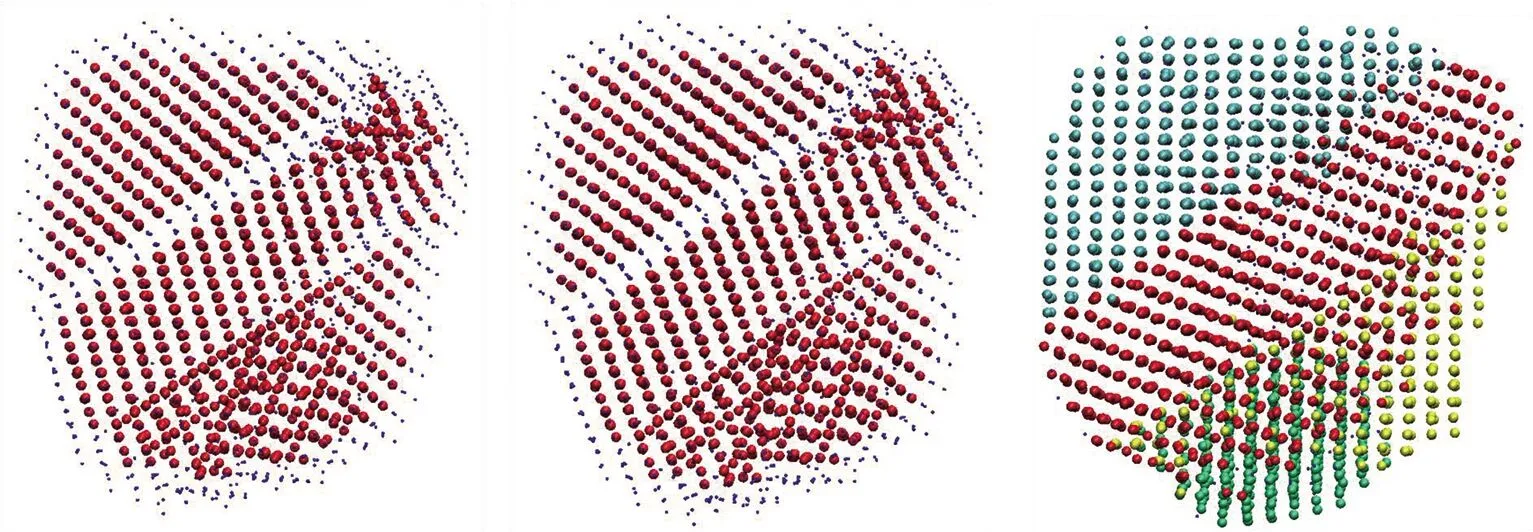
(c) 3 456个Fe原子聚集体

在对2 880 Fe3++4 320 O2-聚集体、2 000 Fe3++ 1 000 Fe2++ 4 000 O2-聚集体、2 496 Fe3++ 2 496 O2-+ 2 496 OH-聚集体与3 024 Fe2++ 6 048 OH-聚集体的局部有序结构识别中，种群平均适应度与最优个体适应度随迭代次数的变化曲线见图4.由图可知，最优个体适应度呈阶跃上升，这是因为只有当新产生的个体比上一代最优个体更优时，最优个体适应度才可能显著提升.在迭代初期，最优个体的更新频率与适应度提升幅值均较高；随着迭代次数的增加，更新频率与提升幅值逐渐减少，最终最优个体的适应度曲线趋于水平.鉴于初始产生个体的随机性，进化方向尚未明确，因此在迭代初期，平均适应度曲线上升较为平缓.随着迭代次数的增加，较优个体的主导作用逐渐显现，平均适应度曲线逐渐陡峭.最终，种群的平均适应度逼近最优个体适应度，表明多种群差分进化算法在解决本文提出的目标函数最大化问题上是收敛的.

4个离子聚集体的识别结果见图5.将算法识别出的离子标记为大尺寸颗粒.整体而言，使用大尺寸颗粒标记的离子排列方式与其对应的晶体结构相似，使用小尺寸颗粒表示的离子则呈现出明显无序的排布.此外，算法识别出的局部有序结构的范围略大于人工框选出的范围，这是因为在聚集体较为无序的表面附近，仍可能存在排列方式与晶体结构相似的少量离子，该算法可以同样对其进行识别.

上述结果验证了本文算法的有效性.在数次迭代后，该算法不仅能够从模拟体系中识别出fcc、hcp、bcc等简单晶体结构，得到与CNA、PTM经典算法相似的结果，也可识别出排布较为复杂的晶体结构，如铁的氧化物、羟基氧化物、氢氧化物.此外，该算法是基于模拟体系与晶体结构相似性进行比对的，故仅提供用于比对的晶体文件即可，无需对数据进行预处理或预训练.

(a) 2 880 Fe3+ + 4 320 O2-聚集体

(b) 2 000 Fe3+ + 1 000 Fe2+ + 4 000 O2-聚集体

(c) 2 496 Fe3+ + 2 496 O2- + 2 496 OH-聚集体

4 结论

1) 结合模拟体系的几何结构与拓扑结构定义目标函数，用于表征模拟体系与模板间重合度.通过多种群差分进化算法，搜索出目标函数最大时的平移距离与旋转角度，从而确定模拟体系中排列方式与晶体结构相似的原子/离子.

2) 采用本文算法，对由Al、Mg、Fe原子分别

(b) 2 000 Fe3+ + 1 000 Fe2+ + 4 000 O2-聚集体

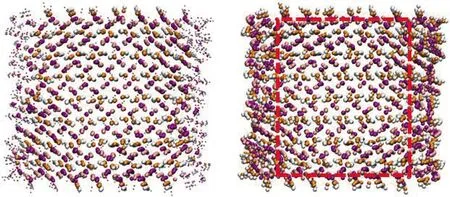
(c) 2 496 Fe3+ + 2 496 O2- + 2 496 OH-聚集体

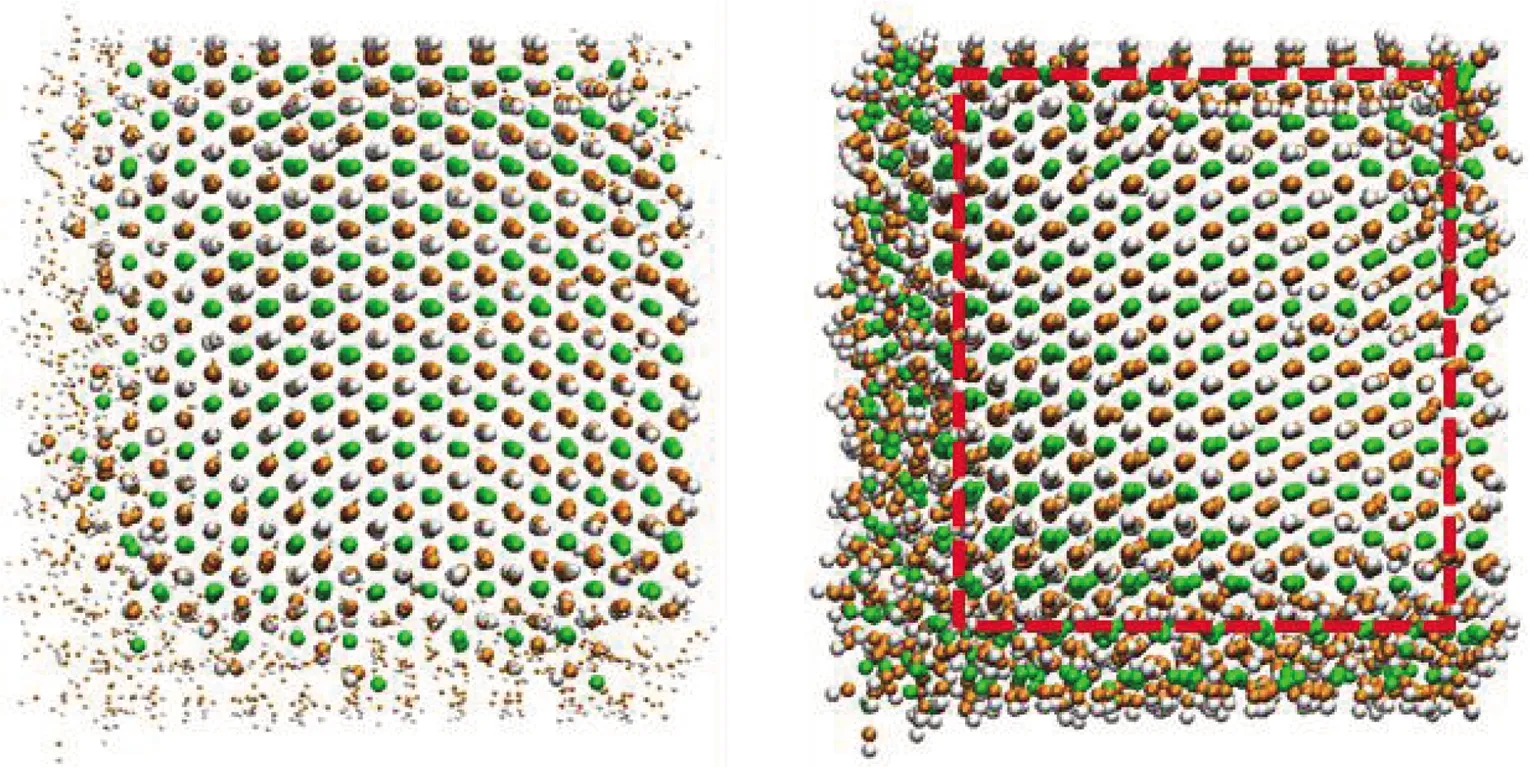
(d) 3 024 Fe2+ + 6 048 OH-聚集体

构成的3种金属单质聚集体进行结构识别，识别结果与CNA、PTM经典算法分类结果基本一致.此外，本文算法还可将聚集体直接分割为多个独立的晶体区域.

3) 对由Fe3+、Fe2+、O2-、OH-离子组成的4种离子聚集体进行结构识别.结果表明，采用本文算法均能搜索出最优的空间变换参数，进而识别出模拟体系中的局部晶体结构.