无人机集群协同探测距离解模糊方法

杨兴家, 段克清,*, 李 想, 祁 炜

(1. 中山大学电子与通信工程学院, 广东 深圳 518107; 2. 空军预警学院, 湖北 武汉 430019)

0 引 言

面对日益复杂的作战环境和作战任务,准确获取战争信息、实现零伤亡是未来武器装备的迫切要求[1]。然而,单平台有人机载预警雷达无法深入敌方做到稳定覆盖探测,且雷达截面积较大及机动性较差,导致战争中易被摧毁造成人员伤亡。而大型无人预警雷达虽然可以保障飞行员安全,但是其机动性差不可避免。随着无人机技术的发展,目前无人机已经逐渐从单平台向集群协同方式转变[2]。无人机系统经过几十年的发展,已经逐步从安全性空域执行情报侦查任务向对抗性空域执行主流作战任务发展。同时,无人机的作战样式已逐步从单平台作战向多平台集群作战方向发展[3-4]。如将雷达布置于无人机集群系统上,便形成分布式无人机集群雷达协同探测系统,可执行共同的任务[5-6]。与传统大型单基无人预警平台相比,无人机集群预警探测具备显著优势[7-8]。首先,更大的天线孔径和空域自由度,可实现更高的目标空间分辨率和更好的杂波抑制性能,同时更窄的主瓣波束可有效对抗主瓣干扰;其次,无人机集群探测时单架无人机所需功率较小,可提供更好的低截获特性,同时具有高机动能力,从而生存能力得到显著提升;再次,多架无人机进行探测可大大提升预警探测系统的任务可持续性,即使单架或多架无人机被摧毁,仍可保持较好的集群整体探测性能;最后,小型无人机具备较低雷达截面积,机动性高,可以穿越山洞、树林等遮蔽环境,深入敌方内部进行探测,起到对大型单基预警平台的补盲作用[9-10]。此外,无人机平台相对廉价,因此可大大降低空中预警探测系统投入成本。综上所述,无人机集群协同探测具备探测范围广、探测精度高、布阵机动灵活等突出优势,因此开展其相关技术研究具有非常重要的军事意义。

空时自适应处理(space-time adaptive processing, STAP)技术是当前各类运动平台杂波抑制和目标检测的关键技术[11]。无人机集群协同探测发现运动目标的前提是强地/海杂波抑制,因此需要利用STAP技术进行空时滤波处理。对于机载雷达而言,由于平台高速运动,主瓣杂波在多普勒域严重展宽。为避免主瓣杂波在多普勒域发生混叠及更方便检测高速运动目标,机载雷达脉冲重复频率(pulse repetition frequency, PRF)往往设置为中PRF(medium PRF, MPRF)或高PRF(high PRF, HPRF),这导致雷达回波存在严重距离模糊[12]。因此,机载雷达回波经STAP杂波抑制和目标检测后,还需要进行距离解模糊才能得到目标真实距离。当前,机载相控阵雷达解模糊的方法主要包括多PRF解模糊法[13-14]、一维集算法[15]、中国余数定理算法[16]和发射脉间编码技术[17]等。其中,多PRF参差变周法通过在同一波位按照两两互质要求发射不同重频相干脉冲进行解模糊,需要在整数范围内求解,因此对距离估计误差较为敏感,同时目标相参积累脉冲数受限;一维集算法列举各PRF测得目标所有可能的模糊距离,再查找目标最可能的重合点;该方法虽然具有较好的解模糊效果,但运算复杂度过大而不利于应用于实际工程;文献[16]提到的基于中国余数定理的目标距离估计算法比一维集算法复杂度低,具有很强的实时性,适合工程上的应用,但其对多目标余数噪声很敏感,无法实现多目标距离解模糊;文献[17]提到的发射脉间编码技术基于Ipatov码,以HPRF发送短脉冲,再针对不同编码信号构造匹配滤波函数进行解码,滤除部分距离模糊信号能量,进而达到距离解模糊效果。因为是在脉间进行编码,所以它只解决了慢时间或多普勒域中的距离模糊问题。除此之外,文献[18]提出基于频率分集阵列(frequency diverse array, FDA)体制的STAP雷达距离解模糊方法,通过FDA的发射导向矢量是距离的函数这个特点可以在距离维引入可控自由度来实现不同距离区杂波的区分,进而达到解模糊的目的,该方法需要利用子空间投影技术和二次距离依赖补偿才能实现模糊距离杂波的分离。在此基础上,文献[19]进一步提出了一种基于FDA体制合成孔径雷达高分辨宽测绘成像中的距离解模糊方法,该方法基于FDA距离维可控自由度,利用频率分集阵列发射导向矢量的距离和角度的二维依赖关系,能在空间频率域区分模糊距离杂波。此外,上述两种解模糊方法均针对FDA体制特点展开,无法直接应用于传统相控阵雷达。近来许京伟等人基于阵元脉冲编码技术,提出一种针对多输入多输出(multiple-input multiple-output, MIMO)体制雷达的距离解模糊方法[20-21]。该方法在阵元间发射傅里叶基正交波形,然后在发射阵元和发射脉冲间增加相位编码,在接收端解码后能够区分不同发射脉冲,从而实现距离解模糊。然而,该方法仅适用于MIMO体制。

不同于传统单基预警雷达,无人机集群协同探测雷达阵列具有大尺寸和超稀疏孔径的特点,其目标回波信号的相位信息不仅与一次相位项有关,还受到二次相位项严重影响。因此,无人机集群雷达阵列回波信号应视为球面波,即存在严重近场效应[22]。在这种情况下,无论是杂波回波还是目标回波,其空域导向矢量均随距离变化而变化。换句话说,用于目标匹配的空域导向矢量信息应该与其真实距离相匹配才能获得目标信号最大增益。基于该特点,本文设计了一种新的距离解模糊方法,即利用不同模糊距离所对应空域导向矢量的差异性,按照不同模糊距离所对应的空时导向矢量形成的权系数分别对雷达回波进行杂波抑制和目标匹配处理,得到多个处理结果,并进行目标功率比较,得到真实目标距离。该方法实现简单,理论上可在单重频条件下实现无人机集群协同探测雷达的距离解模糊处理。

本文首先简要介绍了单基机载雷达空时信号模型,然后进一步推导了近场效应情况下的无人机集群协同探测信号模型,并在此基础上描述了基于近场效应的距离解模糊方法,最后通过仿真数据验证了所提方法的有效性。

1 单平台机载雷达空时信号模型

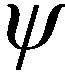
基于Ward报告[24],杂波回波数学模型可表述为

(1)

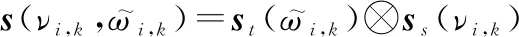
(2)

ss(νi,k)=[1,ej2πνi,k,…,ej(N-1)2πνi,k]T

(3)

根据式(1),待检测距离单元杂波协方差矩阵可表示为

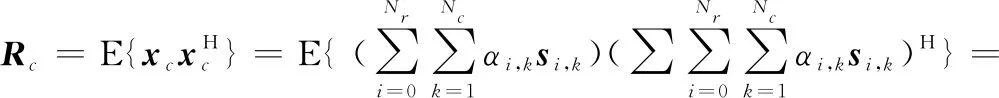
(4)

由式(1)和式(4)可以看到,对于某一待检测距离单元,杂波由地面上Nr个模糊距离的杂波回波共同叠加组成;同样,远距离目标回波也存在严重距离模糊。目标在待检测单元中被强杂波掩盖,因此在进行距离解模糊之前,必须进行杂波抑制处理。STAP技术利用空域(阵元采样)和时域(脉冲采样)二维联合自适应处理,在空时二维平面上可实现对杂波的有效抑制。根据空时最优处理器的算法原理[25-26],最优的空时二维处理器的权矢量w可以表示为

w=μR-1s0

(5)

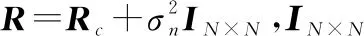
2 无人机集群协同探测距离解模糊方法

传统单平台机载雷达几何模型如图1所示,天线阵列孔径相比于探测距离较小,因此可将目标回波近似为平面波[27],上述空时二维信号模型正是基于回波信号为平面波假设所构建的。对于多平台无人机集群探测雷达而言,假设两架无人机最小安全距离为100 m,共4架无人机,那么无人机集群天线阵列将构成300 m的超大稀疏孔径天线。此时,回波信号不能简单地假设为平面波。根据文献[28],辐射近场区与远场区的分界距离为2a2/λ,其中a为天线孔径。在孔径为300 m的超大稀疏孔径下,若雷达工作在L波段,则其只有在900 km才能近似为远场平面波,而在该距离范围内均为近场区域,需按照与距离有关的近场球面波进行建模。根据这个特点,本文在已有单平台机载雷达信号模型的基础上,对无人机集群协同探测进行空时二维信号的建模,并且根据雷达回波是与距离相关的球面波这个特点,提出一种简单、有效的目标距离解模糊方法。

2.1 无人机集群协同探测空时信号模型

假设有若干架搭载相控阵雷达的无人机以安全距离D并排飞行,其几何关系如图2所示。

在稀疏大孔径近场情况下,雷达回波不再是平面波而必须看成是与距离相关的球面波,此时阵列各阵元接收回波相位受到近场效应严重影响。假设有M架以等间距D线性排列的无人机集群,每架无人机上相控阵天线有N个阵元。以首架无人机第一个阵元为参考阵元,杂波块位于(θ,R1,1)处,第m架无人机第n个阵元与杂波块之间的距离为Rm,n。其他参数定义与图1相同。根据余弦定理有

(6)

则稀疏大孔径阵列中任一阵元相对于参考阵元的时延为

(7)

式中:c为光速。

对

进行泰勒展开并忽略高阶项,可得

(8)

故相位差为

(9)

式中:fc为雷达载频。式(9)中,当满足[(m-1)D+(n-1)d]2≪R1,1时,第二项可以忽略,因此回波可近似为平面波,该情况可视为远场情况。然而,随着[(m-1)D+(n-1)d]2的增大,第二项相位项取值变大,特别是与第一项相位项相比不能再被忽略,因此必须考虑,该情况应视为近场情况。图3为不同波束扫描角情况下无人机集群阵列回波信号的一次和二次相位项。由图3可以看出,当θ=90°时,即波束扫描角位于天线法线方向时,回波一次相位和二次相位项之间相差较小,此时天线近场效应最为显著;θ=45°时,即波束扫描角偏扫较大角度时,回波一次相位与其二次相位项之间差距较法线方向情况变大,但在其近场区域相位差仍然不大,因此同样存在显著的近场效应。

根据上述分析,将式(9)代入到空域导向矢量ss(νi,k),可得近场情况下新的空域导向矢量为

(10)

2.2 基于近场效应的距离解模糊方法

假设系统最大模糊距离次数为L次,当目标位于第p个距离门、第l个模糊距离时,其真实距离为Rl=(l-1)·Ru+pΔR。其中,Ru=c/2fr为最大不模糊距离,ΔR=c/2B为距离分辨率,B为信号带宽,c为光速。

在近场效应下,目标导向矢量将随所在距离变化。若目标所在第l个模糊距离,由式(8)和式(9)可得,目标在各阵元的相位差为

(11)

其中,Rl为目标与参考阵元之间的斜距。此时目标导向矢量为

(12)

其中,

(13)

基于不同模糊距离可以得到一组空时自适应滤波权系数W:

(14)

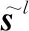
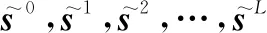
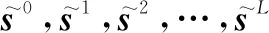
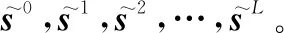
3 仿真分析

本部分对所提无人机集群协同探测距离解模糊方法性能进行仿真验证。本仿真实验无人机阵面放置为正侧视且无人机等间隔分布,单架无人机阵列阵元以半波长等间隔分布。仿真参数如表1所示。根据表1可以计算得到该雷达系统最大不模糊距离为37.5 km,最大距离模糊数为4。

表1 无人机集群雷达仿真参数

3.1 不同导向矢量匹配对方向图影响

假设目标发生1次距离模糊,则分别用不模糊距离、第1次模糊距离、第2次模糊距离和第3次模糊距离对应导向矢量对目标进行匹配,并对其各匹配后的方向图进行对比。

图5为无人机协同探测阵列方向图。从图5可以看出,由于无人机集群阵列为大孔径稀疏阵列,因此其方向图中存在严重栅瓣;同时,由于严重近场效应,各不同距离导向矢量所匹配生成方向图存在明显差异。其中,由图5(b)可以看出,该方向图主瓣宽度明显小于其他3个方向图,同时其副瓣电平也显著低于其他方向图。这是由于目标恰好位于第1模糊距离,因此采用第1模糊距离所对应导向矢量可实现无损失匹配积累。由图5(a)、图5(c)和图5(d)可以看出,其方向图主瓣较图5(b)均有不同程度展宽,副瓣电平也有明显抬升,且距离第1模糊距离越远,由导向矢量失配引起的波形畸变越严重。

3.2 杂波抑制与目标距离解模糊性能分析

本部分通过对无人机集群协同探测杂波建模后的抑制处理,分析并比较利用多个权系数分别进行杂波抑制处理后的目标检测情况。其中,杂波抑制方法选用扩展因子法(extended factored approach, EFA)[30-31]。在本部分实验中,为分析杂波抑制对后续目标积累的影响,设定两个目标,即目标1和目标2,均位于第400个距离门。其中,目标1距离模糊1次,位于空间频率为0、多普勒频率为0.085位置,即位于主瓣杂波区;目标2距离模糊3次,位于空间频率为0、多普勒频率为-0.596位置,即位于副瓣杂波区。

图6为杂波抑制前后的距离-多普勒功率谱图。其中,图6(a)为杂波抑制前距离-多普勒功率谱图,图6(b)～图6(f)分别为采用不同模糊距离所对应空时导向矢量对杂波进行抑制后的距离-多普勒功率谱图。由图6(a)可以看出,在杂波抑制前,两个目标均被杂波掩盖,无法被有效检测。由图6(b)～图6(f)可以看出,经不同模糊距离所对应空时权矢量进行杂波抑制后,主瓣杂波明显变窄,同时副瓣杂波被抑制至噪声电平,可见采用不同权矢量后杂波抑制性能相当;此外,由图6(b)～图6(f)还可以看出,经杂波抑制后,各处理结果中均能检测到两个目标,但由于采用不同模糊距离所对应导向矢量进行目标匹配,各结果中目标功率存在明显差别。具体来说,对存在1次距离模糊的目标1而言,当采用不同空时权系数w0、w1、w2、w3和w4对杂波处理之后,其对目标功率积累分别为-32.87 dB、-19.20 dB、-22.25 dB、-24.71 dB和-22.99 dB。可见,当采用第1模糊距离对应导向矢量进行匹配滤波时目标功率最强,比其他4种情况分别高13.67 dB、3.05 dB、5.51 dB和3.79 dB,因此可判断目标1共发生1次距离模糊。同样,目标2的功率较其他几种情况分别高9.16 dB、4.4 dB、8. 37 dB和6.31 dB,因此可同样判定其共发生过3次距离模糊。

为了探究多个目标到雷达真实距离相同时该算法解模糊性能,本部分实验我们设定两个目标,即目标1和目标2,均位于第400个距离门,距离模糊次数均是1次,两个目标真实距离相同。其中,目标1位于空间频率为0、多普勒频率为0.085位置,即位于主瓣杂波区;目标2位于空间频率为0、多普勒频率为-0.596位置,即位于副瓣杂波区。

图7为真实距离相同的两个目标解模糊情况。由图7可以看出目标1与目标2均在第1个模糊距离处功率最大,分别为-30.53 dB、-20.97 dB,比其他模糊距离大2 dB以上,因此可以判断两个目标均发生1次距离模糊。

3.3 阵元误差对解模糊性能影响分析

为了进一步研究本文提出的方法对阵元误差的敏感程度,本实验分别对理想情况和存在阵元误差情况下的距离解模糊性能进行了对比分析。假设无人机之间定位无误差,仅考虑单架无人机的天线阵元误差。阵元误差主要考虑3%的幅相误差,具体定义为

ξ=[ξ1,ξ2,…,ξN]=[a1ejφ1,a2ejφ2,…,aNejφN]

(15)

式中:ξi服从零均值方差且标准差为3%的复高斯分布;ai和φi分别为各阵元的幅度误差和相位误差,i=1,2,…,N。此外,在该部分实验中,设定目标位于空间频率为0、多普勒频率为-0.596位置,距离模糊2次。

图8(a)和图8(b)分别给出了理想情况和存在3%阵元误差情况下各模糊距离对应目标检测结果图,其中,坐标X、Y与Z分别表示归一化多普勒频率、模糊距离数与目标积累功率。由图8(a)可以看出,在理想情况下,采用第2模糊距离所对应空时导向矢量进行空时滤波时所检测目标功率显著强于其他情况;而存在阵元误差情况时,如图8(b)所示,目标积累功率要略小于理想情况,这主要是由于误差引起的导向矢量失配所致,但此时在模糊距离数为2时目标功率仍明显强于其他模糊距离数的目标功率,分别比模糊距离数为1和模糊距离数为3高8.32 dB和11.78 dB。因此仍可采用本文所提方法进行解模糊处理。

3.4 探测距离与解模糊性能关系

本节通过仿真实验分析了不同探测距离情况下解模糊性能的差异,分别考虑了目标位于第67.5 km、142.5 km、217.5 km、292.5 km和367.5 km这5种典型情况。根据表1参数可以计算得到,上述5种情况所对应目标模糊距离次数分别为1、3、5、7和9。

图9给出了本文方法处理后不同模糊距离数对目标功率积累关系图。由图9可以看出,当目标发生1次距离模糊时即目标位于67.5 km处,其在对应模糊距离所积累目标功率要明显大于其他模糊距离所对应功率,其功率电平要高出相邻模糊距离5 dB以上;当目标分别位于第142.5 km、217.5 km、292.5 km、367.5 km,即分别发生3、5、7、9次距离模糊时,其目标功率较相邻模糊距离积累目标功率分别高7.8 dB、4 dB、1.2 dB、0.8 dB左右。随着目标距离的增加,即目标对应距离模糊数的增加,其在对应模糊距离所积累功率较其他模糊距离所积累功率差异在逐渐减小;本实验说明,当目标位于较近距离情况下,由于近场效应严重,因此采用本文所提方法解模糊性能更为突出;然而,随着目标距离的增加,由于近场效应的不断衰减,本文所提解模糊性能逐渐下降。在实际作战环境下,无人机集群探测的主要目的是深入敌方阵地前沿进行无人侦察预警,此时所需探测距离一般小于300 km,其需求要远低于在后方远距离预警探测的有人预警雷达。因此,本文所提距离解模糊方法在无人机集群预警探测背景下是可行的。

4 结 论

针对无人机集群探测动目标解距离模糊问题,本文根据稀疏大孔径阵列存在严重近场效应这一特性,提出一种简单有效的解距离模糊方法,并经仿真验证了可行性。需要注意的是,当雷达探测距离较远时,阵列近场效应随之减弱;但由于无人机集群主要用于前伸至靠近敌方区域进行探测,因此所提方法仍适用于该应用场景。本文通过空间线性排列多架无人机编队验证了所提解距离模糊方法的有效性,在后续研究工作中将进一步构建空间复杂编队信号模型并验证所提方法。