基于形态学自适应分块的高分辨SAR多特征增强算法

方 澄, 李慧娟, 路 稳, 宋玉蒙, 杨 磊

(中国民航大学电子信息与自动化学院天津市智能信号与图像处理重点实验室, 天津 300300)

0 引 言

合成孔径雷达(synthetic aperture radar,SAR)具有全天时、全天候的对地遥感成像能力,可用于目标检测识别和导弹精确制导等多种任务,在民用和军事领域均得到广泛的应用[1-6]。随着SAR高分辨成像领域的蓬勃发展,基于压缩感知(compressed sensing,CS)理论的稀疏成像类算法[7-9]层出不穷,比如经典的贪婪类算法[7]、贝叶斯稀疏算法[8]以及凸优化(convex,CVX)类算法[9]等。其中贪婪类算法虽运算效率佳,成像精度却受限;而贝叶斯稀疏算法与贪婪类算法截然相反,其运算复杂度高导致速度慢;传统的CVX则在迭代时涉及高维矩阵求逆运算,导致计算效率低。交替方向多乘子法(alternating direction method of multipliers,ADMM)[10]的出现有效解决了CVX算法运算效率低的现状。ADMM结合了多种算法的优点,既具有优越的收敛性又有可分解性,在算法迭代过程中首先分别解决每个子问题,再对子问题的解进行有效调和,从而得到全局最优解。

数学形态学理论为上述问题的解决提供了新的思路[14-21],其主要思想是利用结构元素来遍历并采集图像信息,从而分析各个结构块之间的关系,以便进一步分类识别结构特征[22-25]。传统的数学形态学是采用固定的结构元素进行信息采集和结构识别,但实际的SAR成像场景复杂且散射信息庞大,并具有空间可变性。因此，本文提出利用空间可变形态学实现测地距离结构识别,即基于形态学自适应分块的交替方向多乘子法(morphological auto-blocking alternating direction method of multipliers,MAB-ADMM)实现高分辨SAR多特征表征,该算法采用自适应结构元素实现空间可变,有效增加了目标识别的灵活性。

本文首先分别推导SAR与SAR-GMTIm(ground moving target imaging)模式下回波数据域表达式,从而推导出线性回归模型。针对回归模型的逆问题，本文采用MAB-ADMM来构建正则化解决框架。MAB-ADMM利用空间可变形态学进行自适应分块并建立形态学分块和正则化平滑的混合M/F结构范数,同时利用1范数引入稀疏先验,进而推导其对应的邻近算子,并利用高斯-赛德尔方法来不断并行迭代,更新其积累残差变量。实验部分中的定性分析采用美国空军实验室公布的GOTCHA数据集和SANDIA数据进行实验验证,定量分析采用相变图(phase transition diagram,PTD)进行实验验证,通过对比实验有效验证了MAB-ADMM算法应用于SAR高分辨成像的优越性和可行性。此外，采用MSTAR数据验证了所提算法对分类算法效果提升的有效性。

1 回波信号模型

图1为基于XYZ-O坐标系的SAR和GMTIm模型,SAR平台以速度v沿着预定航线即X方向(方位向)飞行。一般情况下,当雷达波束指向地面观测场景时,即可采集静止场景和运动目标的回波脉冲。

设tn为慢时间变量,则第p个静止散射点和第l个运动目标的位置分别定义为

(1)

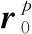
为实现对地面运动目标的检测从而引入多通道天线,设q0(tn)为参考通道的位置矢量,则任意第i个通道可以表示为

qi(tn)=q0(tn)+di

(2)

式中:di是相对于参考通道的空间矢量。

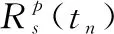
(3)

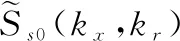
(4)

(5)

通过观察式(4)和式(5),建立统一的矩阵形式:

Y=AX+N

(6)

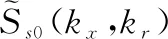
(7)

式中：fd表示多普勒频率;[·]T表示向量/矩阵转置算子。

2 形态学自适应分块ADMM算法

式(6)所示的矩阵等式是典型的逆问题,传统的稀疏恢复类算法,如CVX类算法,求解该等式时通过利用1范数引入稀疏先验[28],从而实现SAR稀疏特征增强,其成像联合最小化形式定义为

(8)

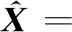
(9)

然后进一步对式(9)所示的联合最小化问题进行求解,该问题可以表示为如下所示的约束性优化问题:

(10)

式中:Θl(X)表示第l个任务的目标函数;λl为每个目标函数对应的正则化参数;ε为根据经验设置的精度阈值。MAB-ADMM延续了ADMM的可分解优势[10],其典型思想是将大的全局问题分解为多个小的局部子问题,从而达到各个击破,分而治之的效果。根据这一思想,引入分裂变量Z,则式(10)可进一步表示为

(11)

(12)

式中：[·]H表示转置算子;ρ>0表示拉格朗日系数;UH为积累残差变量。则其迭代求解形式可表示为

(13)

接下来将根据式(13)所示的流程对所提MAB-ADMM中的全局变量X、形态学结构特征变量Z1、稀疏特征变量Z2以及特征变量各自对应的积累残差变量U1和U2的构建过程进行详细推导和介绍。

2.1 更新全局变量X

全局变量X的更新相当于求解如下所示的联合最小化问题:

(14)

设目标函数为Ω(X),并对目标函数进行进一步的推导得

(15)

式中:Tr[·]是求迹算子。

令dΩ(X)/dX=0,可求其最优解为

Xk+1=(AHA+ρI)-1[AHY+ρ(Zk-Uk)]

(16)

2.2 更新结构特征变量Z1

首先利用空间可变形态学进行自适应分块,形态学中的结构元素是雷达场景/目标检测过程中获取邻域信息的重要手段,因此结构元素的设计对获取各区域相关信息有着不可或缺的作用。不同于传统的空间不变结构元素,变形虫结构元素可以将伪足从指定散射中心向8邻域进行延申,当散射强度变化大时中止扩散,从而有效检测目标结构,达到拟合目标结构的目的。由于SAR检测场景的散射情况复杂,因此首先将观测图像的散射强度归一化为分贝:

(17)

由于结构元素的形状是通过测地距离的方式进行拟合,因此测地长度定义为

(18)

式中:φ=(x=x1,x2,…,xn=y) 表示矩阵W中分辨单元x和y之间的测地路径。含有实参数γ的可变结构元素的距离是

(19)

根据式(19)可进一步定义结构元素为

E(x)={L(x,y)≤r}

(20)

式中:r为结构元素的变化半径。

通过构造的结构元素进一步得到空间可变形态学算子,定义基于结构元素的膨胀和腐蚀算子为

(21)

式中:δ与⊕均表示膨胀算子;ε和⊙均表示腐蚀算子;∨和∧分别表示最大值和最小值算子;(Δx,Δy)为(x,y)的相对位置。膨胀算子可以连接目标中孤立的区域,腐蚀算子可以分离本身非强相关的目标结构。膨胀和腐蚀算子可以进一步推导出开闭运算:

(22)

进而根据式(22)所示算子设计初步的掩膜(Mask)为N=Fη(Fζ)=η(ζ(W)),其中的掩膜已经增强了形态结构信息,聚类的强散射特征会形成不同的形态块稀疏结构,然后通过利用8领域连通性将块结构标记为G块,因此假设所提MAB-ADMM迭代k次,迭代分块后的图像掩膜可写为

(23)

(24)

(25)

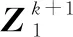
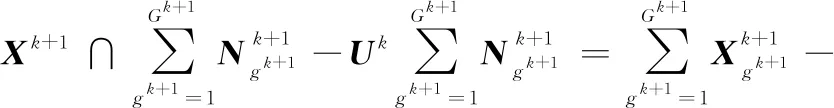
(26)

(27)

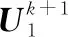
(28)

2.3 更新稀疏特征变量Z2

为进一步引入稀疏先验以增强SAR成像场景/目标的稀疏特征,MAB-ADMM通过引入2范数来实现稀疏表征,Z2的更新过程如下:

(29)

(30)

综上所述,本文所提MAB-ADMM的具体流程如下。

3 实验验证

在本节中,将利用多种实验数据验证所提MAB-ADMM的各项性能,以及与其他现有方法,如基于1范数的ADMM稀疏成像算法、基于传统稀疏组LASSO的ADMM,进行定性和定量比较。并且验证了MAB-ADMM在实际分类应用中可有效提升分类算法的准确率。

3.1 仿真多形态复数据成像对比实验

3.2 SANDIA实测数据对比

本组实验采用SANDIA实测数据来验证所提MAB-ADMM的优越恢复性能,图3(a)为经过0.7降采样,5 dB信噪比处理后的SANDIA实测数据,为地面路径与绿化带。图3(b)为经LASSO-ADMM处理后的成像结果,可见稀疏效果明显,但不足之处是目标内部结构不够连续,因此待背景稀疏干净之时,内部结构将更加稀疏。图3(c)为经SGLASSO-ADMM处理后的成像结果,可见目标内部的结构连续性得到了有效提升,不过仍不够完善。图3(d)为经本文算法处理后的成像效果,可观察左下角目标,结构连续性提升明显。该实验证明了MAB-ADMM应用于实测数据的有效性和可行性。

3.3 定量对比实验

本组实验中采用相变图[29]的方法对MAB-ADMM和其他方法进行比较。实验采用图2所示的仿真形态数据进行蒙特卡罗实验,验证在不同参数变化下不同算法与参考图的相关度,从而验证不同算法的恢复性能。图4为3种算法降采样-SNR的相变图对比,通过经验设置统一阈值,低于阈值的低相关度将被认为是不可恢复的,即如图中左半部分蓝色所示,高于阈值将按照颜色深度判断相关度大小,颜色越深,即越靠近右上角部分的红色视为相关度最大,恢复性能最好。由此可见,所提MAB-ADMM的恢复面积更大,性能相对最佳。本组定量实验有效验证了所提算法相较于传统稀疏恢复算法和结构恢复算法的优越性。

3.4 分类效果提升实验

本组实验中采用MSTAR数据,对MAB-ADMM应用于实际分类时提升分类结果的有效性进行验证,并同时给出部分数据的特征增强结果。实验采用7类数据,其中典型3类数据如图5所示,本实验利用MAB-ADMM调整不同参数对图像进行处理,由于数据集十分庞大,因此给出典型的处理后图像如图6所示。其中图6(a)为本文所提算法成像结果,图6(b)为经典LASSO-ADMM成像结果,图6(c)为SGLASSO-ADMM成像结果。图中选取较为明显的对比部分用红框进行标识,值得一提的是,由于本数据成像场景中噪声环境庞大且复杂,因此LASSO模型的稀疏优势并未很好地体现,对比可知LASSO-ADMM的恢复(见图6(b))均难以区别目标和噪声,导致目标结构损失十分严重。SGLASSO-ADMM的恢复(见图6(c))在结构恢复方面明显强于图6(b),不过由于欧式距离的简单分块影响,导致目标轮廓提取仍然有一定的缺陷,从图6中红框标识部分可见,此算法的结构丢失部分明显大于所提算法。表1为MAB-ADMM分类结果统计,分类算法采用主成分分析网络(principal components analysis net,PCANet)[30],PCANet是一种结构简单、训练高效的图像分类算法,可以提取图像的纹理特征,将图像的纹理特征作为支持向量机(support vector machine, SVM)分类器的输入,最终产生分类结果。本组实验在训练数据集上使用MAB-ADMM对数据进行了扩充,在测试数据集上使用3组不同的参数对处理后图像的分类结果进行测试,3组不同参数对于准确率的提升分别为3.00%、3.59%和3.66%,准确率总的提升为6.00%,可以看出MAB-ADMM可以使得图像的轮廓更加清晰,减少噪声的影响,有效提升分类算法的准确率,具有很好的应用价值。

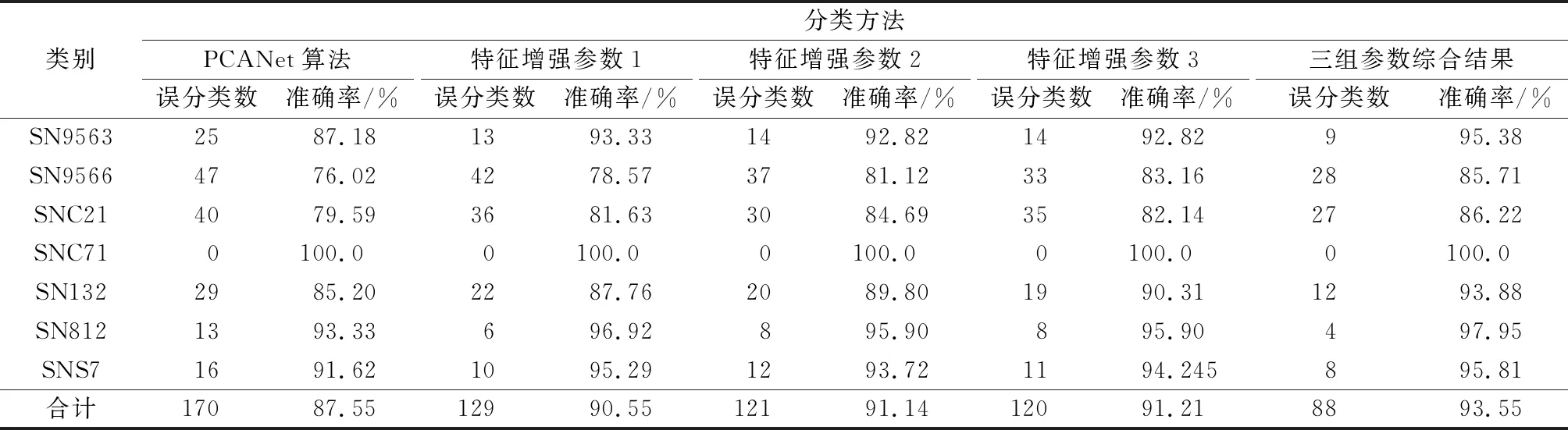
表1 MAB-ADMM分类结果统计

4 结 论

针对基于LASSO模型的SAR稀疏成像算法易丢失弱散射点,而稀疏组LASSO模型由于欧式距离分块方式造成结构增强效果不佳的问题,本文提出一种基于形态学自适应分块的MAB-ADMM来实现高分辨SAR多特征表征,该算法通过空间可变形态学利用测地距离实现良好的结构识别,并进行分块迭代,建立M/F混合范数引入结构先验。此外,为保留稀疏增强性能,采用传统1稀疏范数引入稀疏先验。有效实现多特征增强。仿真复数据和实测SAR成像结果验证了所提算法的有效性和优越性,MSTAR数据分类实验验证了所提算法可有效提高分类算法准确率。