基于脑电信号的情绪识别

李贤哲 暴伟 谢能刚

0 引言

人类在日常生活中的情感交流活动是必不可少的，情绪不仅可以维系人与人之间信息交流的密切关系，更是一种适应生存的基本保障。在人机交互与人工智能技术的相互发展下，产生了一种与情感相关，并施加影响情感的计算，即为情感计算，目的是让机器能够自动感知、识别、分析以及推测人的情绪，使机器拥有更好的智能化交互，提高人性化水平的能力[1]。情绪识别是情感计算中的关键环节，通常用生理或行为特征指标对服务用户的情绪状态进行判断。

目前情绪识别研究中的分类模型主要有离散情绪模型和维度情绪模型[2]。 离散情绪模型定义的数量多为2～8个，目前一般公认的基本情绪是Ekman[3]提出的快乐、愤怒、悲伤、恐惧、惊讶和厌恶。维度情绪模型是将情绪定义在二维、三维或多维坐标空间上的点，点与点距离越近说明情绪的相似程度越高，这种方式能够更好地表达情绪之间的关联程度。二维情绪模型中比较常用的是以Russell与Lang为代表的效价-唤醒度模型[4]，效价表示情绪的愉悦程度，唤醒度表示情绪的激活程度。三维情绪模型是在二维情绪模型的基础上添加优势度，表示主体对情景和他人的控制状态[5]。

情绪的识别可以分成三类：(1) 非生理信号的识别方法，侧重分析面部表情[6]、语音语调[7]和动作特征[8]。该方法不需要特殊设备，但极易伪装，面对受过心理训练的对象时，被测对象能够很好地掩盖或夸大自己真实的表情、语调和动作。(2) 侧重分析外周自主神经系统在不同情绪状态下的变化，如心电[9]、肌电[10]和心率脉搏[11]等，与非生理信号的识别方法相比，外周生理信号可以提供更准确、更复杂的信息作为参考依据，但通常缺乏一个合理的衡量标准。(3) 使用脑电信号(electroencephalograph,EEG)，其描述大脑神经元活动从中枢神经系统传递至大脑皮质，记录大脑皮质的电位变化。由于人的大脑与情绪密切相关，EEG恰好可以作为大脑和情绪之间沟通的桥梁，因此近年来使用EEG研究情绪识别逐渐成为热点话题。

EEG的情绪识别流程主要有信号采集和信号处理，两个流程相结合即称为模式识别的过程。信号采集的好坏往往决定着数据的好坏，刺激方式作为展示给被试激发不同情绪状态的根源性因素，其强弱会直接影响情绪EEG的诱发程度。目前激发情绪的刺激方式有气味、文字、图片、音乐和视频等，其中视频采用视听结合的方式，且对环境、设备和成本等因素要求较低，因此本文选择视频作为诱发刺激方式。EEG的处理流程主要有预处理、特征提取、分类识别，其中特征提取是整个模式识别的关键因素。特征提取主要有时域、频域、时频域三种类型，张冠华等[12]全方面介绍了情绪识别领域中这三种类型相关的特征提取方法，并对每种方法做出相应的数学逻辑推导过程。鉴于不同类型的特征提取方法反映EEG不同方面的信息，且近年来非线性动力学特征也逐渐应用于EEG的情绪识别，因此本文从时域、频域和非线性三个方面提取EEG的有效特征。EEG情绪的分类识别通常用到机器学习中的有监督学习，有监督学习是对已知有分类概念的训练样本学习，尽可能对训练集外的样本进行分类预测，常用的分类器有神经网络[13]、支持向量机[14]、K-最近邻(K-nearest neighbor,KNN)[15]等，其中KNN在处理小样本数据中优势显著，在实时检测识别中应用较好，因此本文选择KNN分类器对不同的特征进行情绪识别。

能够快速准确识别不同人的情绪状态是情绪识别目前存在的难点。本文拟通过设计一种电影片段诱发实验，采集被试在恐惧、愤怒、悲伤和快乐四种情绪下的EEG，经过上述信号处理流程，目的是论证情绪之间是存在区分性的，并通过比较分析不同特征的分类性能来寻找最优的情绪识别特征。

1 脑电信号的情绪采集实验

1.1 脑电实验设备

EEG的产生是放置在头皮表面的电极探测不同位置的电势差得到的。本文选择32导非侵入式电极，电极分布按照国际标准10-20系统进行排列。EEG按照频率特征可以划分为5种频带，即Delta(0.5～4 Hz)、Theta(4～8 Hz)、Alpha(8～13 Hz)、Beta(13～30 Hz)和Gamma(30～47 Hz)频带，每种频带代表不同的大脑活动区域和特征状态。

本文使用E-prime制作不同情绪视频呈现给被试，被试产生的EEG采用软件Brain Vision Recorder进行实时记录。将记录完整的EEG导入分析软件Brain Vision Analyzer2.0中进行信号的预处理，最终将纯净的EEG导入到Matlab中进行后续操作。

1.2 实验素材

对恐惧、愤怒、悲伤和快乐四种情绪的相关视频进行收集、评价和筛选，每种情绪电影找出11个情绪片段，每个片段时长为1 min，统一时间长度是为了在进行数据处理时更加方便。考虑到几分钟的视频片段不容易激发被试情绪，尤其是悲伤情绪，情绪铺垫的时间较长，那么选用包含所有情绪段的完整情节电影片段对情绪的研究或许更为合适。不同情绪电影标记的情绪段和实验时长如表1所示。《狂蟒之灾》片段选取时间范围为正片中的第34分30秒到第83分30秒，即恐惧情绪实验时长为49 min；《南京大屠杀》片段选取时间范围为第31分30秒到第141分30秒，即愤怒情绪实验时长为70 min；《唐山大地震》片段选取时间范围为第3分到第128分，即悲伤情绪实验时长为125 min；《赵本山小品三部曲》选取卖拐、卖车、功夫三部搞笑小品合集，快乐情绪实验时长为40 min。

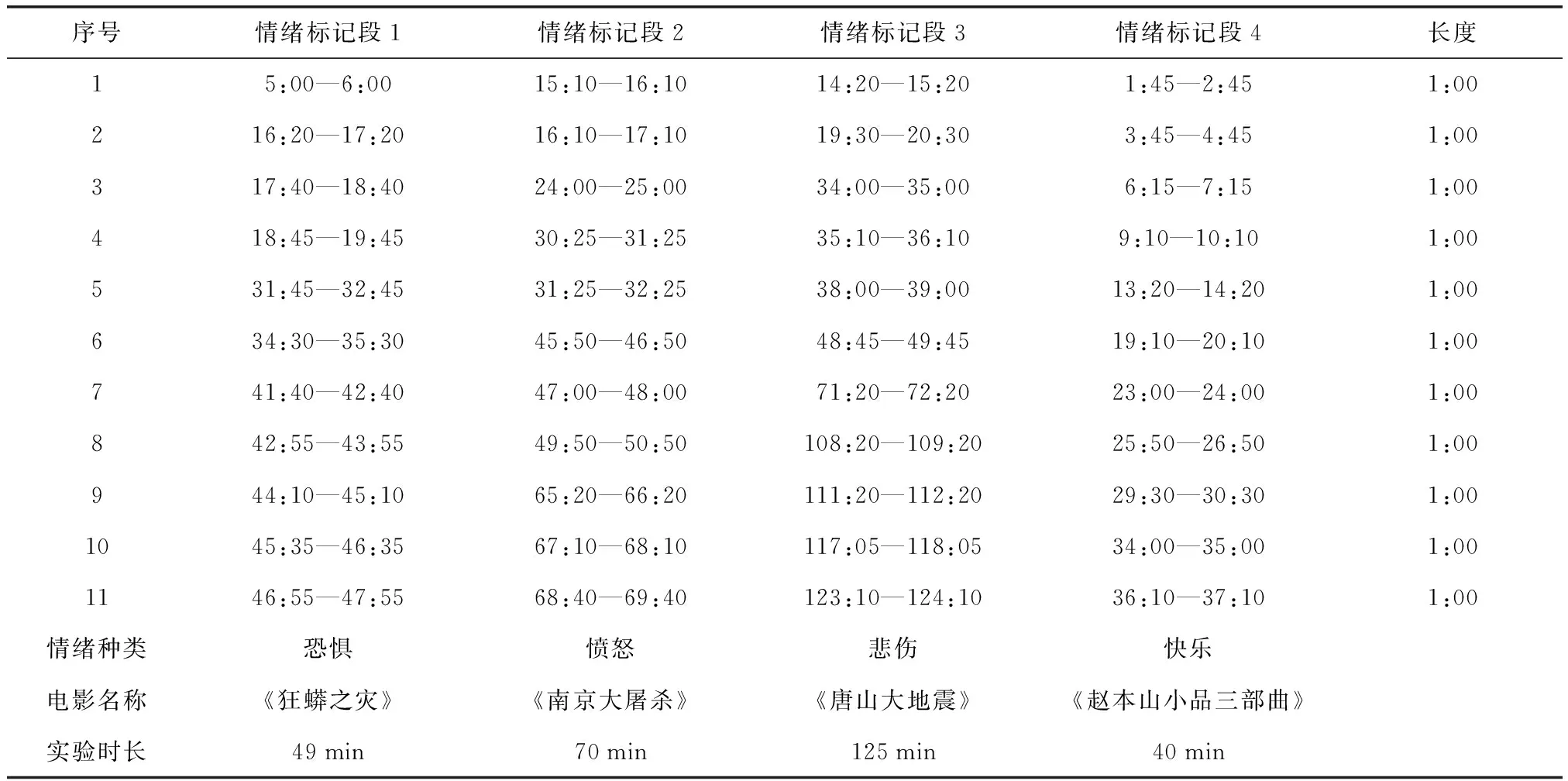
表1 视频诱发情绪材料Table 1 Video induced emotional materials

为保证实验的严谨性，实验结束后从被试主观的角度逐一重现上述电影中标记的情绪片段，被试观看后通过回忆当时的情绪感受并在评估表上进行打分。评估表是根据SAM三维情绪量表对效价-唤醒度-优势度进行1～9的分值打分。信度是客观评估测评有效性的一种方式，本文使用克隆巴赫信度系数，应用SPSS软件分别对每种情绪计算11个片段间的信度值。快乐情绪的信度值为0.742，悲伤情绪的信度值为0.798，愤怒情绪的信度值为0.839，恐惧情绪的信度值为0.852。通常信度值系数大于0.7，说明数据之间关联程度较高，本文4种情绪下的信度值系数都高于0.7，在一定程度上能够说明该量表的有效性。

1.3 实验对象

本次实验招募9位被试者参与实验，均为右利手，其中男性6名，女性3名，年龄为(25±1.7)岁，视听力正常，无烫发染发，无精神障碍和脑损伤等疾病史。每位被试需进行4次实验，每次实验之间间隔1 d。被试到达实验室后需要告知实验目的、实验步骤、风险和注意事项，并签署实验知情同意书。

1.4 实验流程

在正式实验开始时给被试提示实验过程中的相关注意事项，接着让被试保持一段平静状态，开始记录信号；当屏幕出现时间为5 s的‘+’符号时，提示被试即将进入实验；接着跳转到电影进行播放，并在电影结束后对记录的信号数据进行保存；随后依次重现11个情绪片段材料，按照SAM量表让被试对自己当时的情绪感受进行主观评价；最后实验结束。每次情绪实验重复上述流程，按照快乐、恐惧、悲伤和愤怒依次进行实验，且每种情绪实验之间均间隔1 d，防止被试因连续洗头、实验产生厌倦和疲劳。

2 脑电信号的处理与分析

2.1 脑电信号的预处理

原始信号需要采用放大器对电压幅值较小的EEG进行放大，但常常被幅值更高的伪迹信号所掩盖，预处理的目的就是将大部分伪迹信号“消灭”，将EEG从伪迹中“解放”，从而达到除噪的效果。本文使用Analyzer软件进行预处理，采样频率为500 Hz，处理步骤依次如下。(1) 转参考：以双侧乳突TP9、TP10替代Fz作为参考电极，最终记录电极个数为30个。(2) 滤波：情绪EEG通常设置频率宽度在0.5～47 Hz之间，滤除剩余不必要波段频率信号，使波形更清晰。(3) 眼电纠正：使用独立成分分析(independent component analysis,ICA)可以很好地纠正眼电伪迹幅值大、频率低的情况。(4) 伪迹去除：找出实验中由于设备故障导致导联漂移或被试身体动作产生较为严重的肌电伪迹并去除。

预处理后，对情绪段信号按照步长为5 s一个样本数据进行划分(1个样本数据的行包含2500个采样点，列包含30个通道)，因此每个情绪段包含12个5 s的样本数据，每种情绪包含132个样本数据。

2.2 脑电信号的特征提取

2.2.1 时域类型的特征提取方法

针对EEG任一样本数据的时间序列，使用三种时域方法计算特征，公式如下。

标准差：

(1)

式中：xi为时间序列中第i个采样点的值；μx为当前时间序列的均值；N为时间序列的长度，本文为2500。

均方根值：

(2)

一阶差分绝对值的均值：

(3)

2.2.2 频域类型的特征提取方法

功率谱估计(power spectrum estimation,PSE)是对平稳随机信号的能量随频率变化的一种估计方式[17]，基于周期图法中PSE的方差最小化问题，通常有平均和平滑两种途径进行改进。平均是对时间序列长度为N的样本数据进行不重叠平均分段，分别计算每段功率谱后再迭加平均，该方法称为Bartlett法(分段平均周期图法)[18]。平滑是选择合适的窗函数与计算出的功率谱进行卷积，最典型的方法为Welch法。

(1) 改进Bartlett法(加窗平均周期图法)：加窗平均周期图法是在Bartlett法的基础上添加平滑途经，通常合适的窗函数可以减少频谱泄漏，改善谱曲线的光滑性。由于汉宁窗[19]对非周期的连续信号应用较好，本文选择汉宁窗w(n)作为加窗函数，M为窗口长度。

(4)

改进Bartlett法[20]的算法流程如下：

① 对数据进行不重叠分段。假设时序长度为N的信号x(n)，按照窗口长度M分成互不重叠的L段，则N=ML。

② 对每段数据进行加窗计算振幅的平方，得到每段信号的谱估计，则第i个片段的谱估计为：

(5)

式中:ω为频率；U为归一化因子。

③ 对L个片段的谱估计求平均后进行对数处理，得到不重叠分段平均谱估计作为整个样本数据的谱估计，单位转换为dB，取对数的目的是减小高低振幅成分之间所带来的差距。

(6)

(2)Welch法(加权交叠平均法)：Welch法是一种介于平均和平滑两种途径之间最佳折中的方法，其采用重叠加窗的功率谱估计通常比不重叠加窗的效果更好，谱曲线更平滑。本文对样本数据按照2∶1的比例进行重叠分段，即前后两段信号间有一半的重叠部分。Welch法的算法流程[21-22]与改进Bartlett法相似，不同之处为：流程①中对数据进行的是重叠分段，且假设重叠长度为G。流程②中计算第i个片段的谱估计为：

(7)

本文使用改进Bartlett法和Welch法计算样本数据Delta、Theta、Alpha、Beta和Gamma 5种频段的PSE，并对其结果向量求均值，得到该样本数据整体PSE的均值，将向量转换为一个具有代表性的数值作为特征。

2.2.3 非线性的特征提取方法

EEG是一种非线性、不规则、非平稳的随机信号，传统时域或频域的方法只能反映EEG的某方面特征，使用非线性动力学方法，可以更加全方面地认识EEG的特征。熵，在衡量非线性系统复杂程度上优势显著，本文选取近似熵(approximate entropy,ApEn)和样本熵(sample entropy,SampEn)计算特征值。

(1) 近似熵：ApEn是用来检测信号的波动性和新信息产生的概率，是对时间序列复杂程度密切相关的系统性度量。定义为相似向量从嵌入维度m增加到m+1，能够继续维持其相似性的条件概率，嵌入维度m可以理解为切割出时间序列中m个数据点[23]。物理意义为当嵌入维度m变化时，产生新模式的概率越大，ApEn值越大，时间序列的复杂程度越高。ApEn的算法过程如下[24]：

① 设原始信号的时间序列为{x(1),x(2),…,x(N)}，长度为N，按顺序依次对第i个元素重构m维向量Xm(i)，Xm(i)={x(i),x(i+1),…,x(i+m-1)}，其中1≤i≤N-m+1。对任意的两个重构向量Xm(i)和Xm(j)，计算两向量间的距离相似度d[Xm(i),Xm(j)]，其中i,j=1,2,…,N-m+1且i≠j。

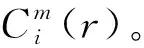
(8)

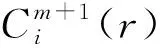
ApEn=φm(r)-φm+1(r)

(9)

(2) 样本熵：SampEn改进了ApEn存在依赖自身数据长度的缺点，具有一定的独立性、一致性等优点，因此理论上SampEn的精确度更高，且运行效率也有一个较好的提升。样本熵的算法过程如下[25]。

① 与ApEn的步骤①类似。不同之处：当前计算第i个元素片段序列时，在不包含自身相同向量的情况下，两个不同向量间的距离计算次数为N-m。

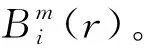
(10)

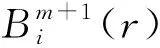
SampEn=lnAm(r)-lnAm+1(r)

(11)

对于ApEn和SampEn中参数的选择，嵌入维度m一般选取1或2，相似容差边界r的选择范围为(0.1～0.25)×std，其中std为时间序列的标准差，即式(1)。

2.2.4 特征归一化

由于被试间存在个体性差异、评价方法存在有量纲和无量纲单位的差异、不同方法对结果映射范围的差异，这些差异会影响数据的分类性能，因此在计算出特征值后进行归一化处理。通常归一化是将数据统一映射到[0,1]的区间内，使不同方法的特征值可以在同一个量级上进行分类。特征值归一化的公式为：

(12)

式中：e为经过特征提取后得到的特征值矩阵；min(e)、max(e)为每个通道特征值列向量的最小值、最大值。本文在特征提取的过程中得到每位被试、每种情绪的特征值，其维度为132×30，4种情绪组合得到特征值维度为528×30，按照通道特征值列向量进行归一化处理，最终得到15个不同的归一化特征值矩阵。

2.3 脑电信号的分类

在情绪识别的过程中，目标是利用分类算法对能够反映情绪的特征进行正确分类预测。KNN是机器学习中较为简单、理论成熟的一种无参数算法模型，核心思想是“物以类聚”，属于有监督学习的一种。算法原理：给定一个已知分类的训练样本，计算测试样本与所有训练样本之间的距离，找出与测试样本中最近的K个训练样本，将占比最多的训练样本类别作为预测测试样本的类别[26]。其中，欧式距离能够很好地表达数据空间中两点间的直线距离，ei表示测试样本中第i个点，j表示划分出训练样本的个数，ek为训练样本中第k个特征值，且k∈(1,j)：

(13)

KNN的缺点主要是样本数据不均衡时，可能导致分类效果欠佳，同时每次需要计算测试数据到所有样本数据的距离，对于数据量偏大或数据维度较高的情况，计算时间较长。本文在每种类别样本均衡的情况下，采用离线的模式识别，因此不影响分类性能。K是KNN算法中唯一需要手动选取的参数，K过小容易造成过拟合，K过大容易造成欠拟合，因此K的选取会影响算法的分类性能。

3 结果分析

为方便结果展示与分析，对经过特征提取后得到的15种有效特征采用简称的形式，如表2所示。本文在进行信号采集时通道电极一般用channel1、channel2……进行表示。

表2 特征及缩写简称Table 2 Features and Abbreviation

3.1 四种情绪状态的特征归一化盒图

在对脑电数据进行特征提取并归一化后，为了观察情绪之间的区分性，选用时域特征中的均方根特征画出被试6的四种情绪状态下30个通道的特征值盒图，如图1所示。图中展示了悲伤、愤怒、恐惧和快乐四种情绪状态下的特征值，每种情绪每个通道包含132个特征值。

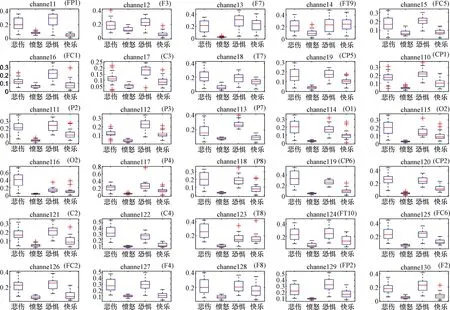
图1 四种情绪状态下的通道特征值盒图Figure 1 Channel eigenvalue box plots in four emotional states

通过观察不同通道的特征值盒图可以发现，情绪之间存在区分性。判断情绪区分性的标准：盒图中样本点数据集中度较高的箱体部分，存在明显的错位现象，判断结果如下。

(1) 在channel5、18、22等通道盒图中发现，悲伤和恐惧情绪的特征值整体上比愤怒和快乐情绪的特征值高。以channel22为例，悲伤特征值的箱体区间为0.25～0.42，恐惧特征值的箱体区间为0.2～0.3，愤怒特征值的箱体区间为0.04～0.07，快乐特征值的箱体区间为0.05～0.12，可以发现悲伤和恐惧特征值的箱体区间最小值高于愤怒和快乐特征值的箱体区间最大值，因此可以判断悲伤、恐惧与愤怒、快乐之间存在区分性。

(2) 在channel2中可以发现快乐特征值的箱体区间最大值位于0.1以下，而其他三种负性情绪特征值的最小值都高于0.1，因此能够判断(1)中的愤怒和快乐情绪可以相互区分。

(3) 在channel16中可以发现悲伤特征值的箱体区间最小值位于0.2上方，而其余三种情绪特征值的最大值位于0.2下方，因此能够判断(1)中的悲伤和恐惧情绪也可以互相区分。

3.2 不同特征使用KNN四分类的识别效果与分析

本文KNN的参数K设置为2，进行恐惧、愤怒、悲伤和快乐情绪的四分类识别。针对个体被试，数据维度为528×(30通道+1标签)；针对总体被试，数据维度为(528×9被试)×(30通道+1标签)。对个体或总体数据进行分类时，都是将个体或总体数据随机划分为70%的训练集和30%的测试集，对此过程循环100次，每次都重新随机划分训练集和测试集，将循环100次的流程称为一轮，最终平均准确率为一轮准确率的均值。

3.2.1 基于时域特征的分类结果与分析

9位被试三种时域特征的个体被试平均分类准确率柱状图如图2所示，图中使用FD特征进行分类得到的个体平均准确率全都保持在96%以上，且大部分被试的FD特征识别效果好于其他两种特征。RMS和std特征平均准确率受个性化差异影响较为严重，被试3的两种特征准确率都没有超过90%，而被试8的两种特征识别率都在99%以上，不如FD特征分类结果稳定。

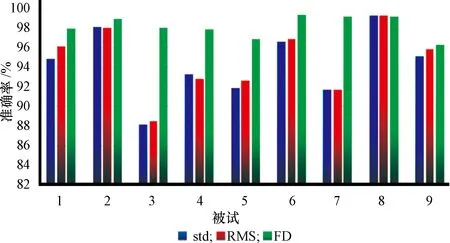
图2 三种时域特征的个体被试平均分类准确率Figure 2 Individual participant average classification accuracy of three time domain features

选择上述三种时域特征，对被试6的第29通道和第5通道画出三维特征值散点图，如图3所示。图中第一维坐标X轴表示std特征，第二维坐标Y轴表示RMS特征，第三维坐标Z轴表示FD特征。从第29通道的三维主视图可以看出，快乐情绪的三维特征值都较低，且数据点较为集中；愤怒情绪的std、RMS特征值较低，FD特征值数据点呈直线扩散；悲伤和恐惧情绪的特征值从该视图观察发现重合，两种情绪存在不可分性。为了区分悲伤和恐惧情绪，从第5通道的三维俯视图中观察到，恐惧和悲伤特征值从原点处数据点分叉，能够说明悲伤和恐惧情绪同样存在区分性。

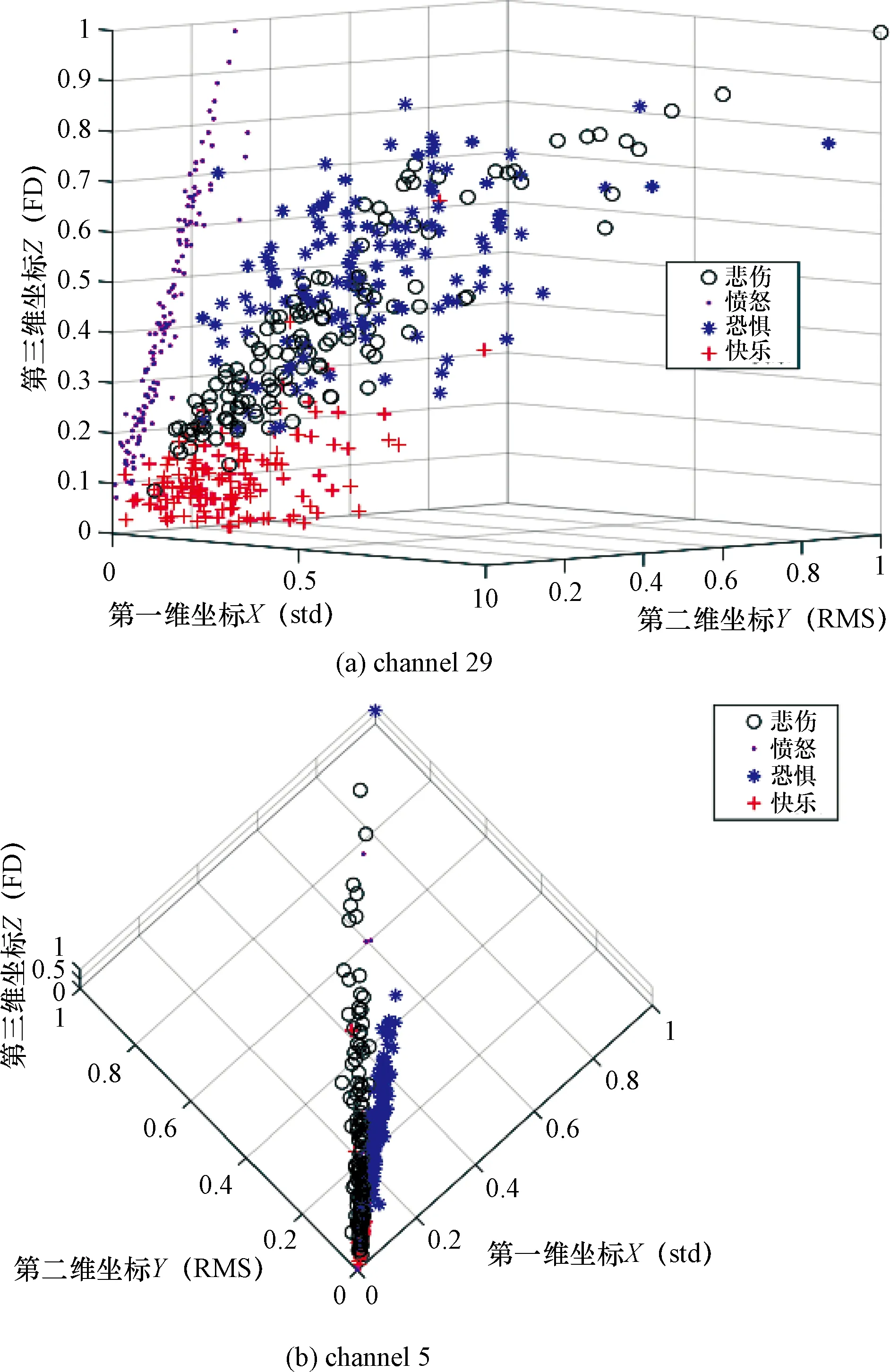
图3 三维特征值散点图Figure 3 Three-dimensional eigenvalue scatter plot

根据9位被试三种时域特征的总体平均分类准确率发现，std和RMS特征识别效果与FD特征相比相对较差，最高准确率没有超过90%，FD特征平均识别率达到95%，识别效果在时域特征中最佳。

3.2.2 频域特征的分类结果与分析

频域特征中使用改进Bartlett法和Welch法计算Delta、Theta、Alpha、Beta和Gamma频带特征的总体被试全通道四分类平均准确率，如表3所示，可以看出不同频带的情绪识别能力存在显著差异。

①Bar_1、Bar_2、Wel_1和Wel_2的平均准确率都低于60%，识别效果很差；Bar_3和Wel_3的识别效果比前两个频段特征高出5%以上，但相较于时域特征，识别能力普遍较差；Bar_4、Bar_5、Wel_4和Wel_5的平均准确率都高于92%，说明分类识别效果较前三个频带特征显著提升的同时又具有稳定的识别能力。由此可以得出Beta和Gamma频带特征在情绪四分类中能够更稳定有效地激发情绪。

②对比Bar_5与Bar_4，Wel_5与Wel_4发现，两种方法的Bar_5和Wel_5识别效果均优于前者，且平均准确率的差值均大于2%，说明Gamma频带特征的情绪四分类识别效果比Beta频带特征好，符合Li等[15]和党杰[27]对不同频带特征贡献度的研究结果，其结果同样发现gamma频带特征的贡献度最高，而Beta频带特征的分类准确率仅次于Gamma频带特征。

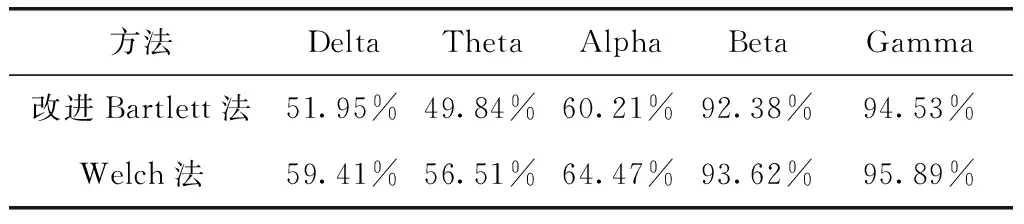
表3 十种频域特征的总体被试平均分类准确率Table 3 Overall participant average classification accuracy of Ten frequency domain features

③ Welch法的Delta、Theta和Alpha频带特征的平均准确率比改进Bartlett法高出约5%，在Beta和Gamma频带高出1%以上，可以说明Welch法的识别效果显著优于改进的Bartlett法，更契合KNN分类算法对情绪的识别。

3.2.3 非线性动力学特征的分类结果与分析

根据9位被试两种非线性特征的总体平均分类准确率发现，SE和AE平均准确率均高于90%，识别结果较好。由于SE与AE之间的平均准确率差值小于1%，同改进的Bartlett法和Welch法频带特征准确率差值相比，差距过小。汤明宏[28]对三种情绪分别使用AE和SE计算出分类准确率，结果得出SE与AE的差值小于1%情况相同，说明AE和SE都适用于情绪识别，但识别效果可能不存在太大的差距。

4 结论

利用Welch法得到的Gamma频带特征和一阶差分绝对值的均值特征作为最优特征，能够快速准确地识别不同被试的情绪状态。并通过RMS特征值盒图和时域特征的三维特征值散点图可以直观验证，四种情绪之间区分性依然很高。以上结论充分说明了使用EEG的客观手段能够对不同情绪进行正确区分。本研究探寻大脑在不同情绪下的信号规律，在面对抑郁症或不善于情绪表达的患者时，能够提供客观有效的评估手段作为辅助治疗。在以后的研究中，提高分类精度和计算效率是脑机接口和情感计算面临的重要挑战。