基于改进二维随机游动的跟踪区域列表优化

陈发堂, 贾俊文, 张杰棠, 杨 玲

(重庆邮电大学通信与信息工程学院, 重庆 400065)

process

0 引 言

在5G网络中,核心网会不停定位用户设备(user equipment, UE)的位置以便于及时发送呼叫请求,这个过程就叫做移动性管理。移动性管理包含位置管理和终端呼叫。位置管理是指UE会不断向网络侧报告其当前位置,终端呼叫是指网络侧会在寻呼区发送广播信号来搜寻被叫UE。但是随着用户剧增和5G网络架构的扁平化,大量用户在网络架构中进行位置变换以及收到寻呼会增加网络负担,造成通信延时,通信错误率增高等问题,因此低效的移动性管理问题亟待解决。在5G架构中,移动性管理方案把整个寻呼区域分成多个跟踪区列表(tracking area list, TAL),每个TAL又包含很多个跟踪区域(tracking area, TA),其中TA内又包含多个小区。当UE在同一TAL内移动时,就不会发生位置更新过程。而在传统的TA方案中,用户只要穿过TA就会发生TA更新(TA update， TAU)过程,因此相比于传统TA方案,TAL方案大大减少了信令消耗。而在终端呼叫方案中,网络侧会同时向TAL内所有小区发起广播。因此，TAL虽然能在一定程度上减少TAU信令消耗,但却增加了寻呼信令消耗。在设计TAL时,要首选考虑到进行TAU信令和寻呼信令的总和,TAL内包含的小区总数越多,相应的TAU信令会减少,但寻呼信令会增加。相反地,TAL内包含的小区数越少,TAU信令会增加,但是寻呼信令会减少,因此TAL的最优化设计是一个非确定多项式难题。

目前已有大量的工作研究TAL的最优化设计,分为静态和动态以及动态和静态结合3类研究方法。第1类静态设计方法中,TAL分配不考虑用户的运动特征。文献[7-8]提出一种局部搜索算法和经验算法,文献[4]和文献[9]分别提出一种启发式粒子群算法和一种多目标约束优化算法,用以解决N-P难题组合优化问题,但这些优化算法只有在每个TA中仅包含一个小区才适用。

第2类动态和静态结合研究方法中,文献[10-11]提出一种新型分布式TAL规划算法,用变阶马尔可夫链为UE分配TAL,但该算法假设一个TAL中仅包含一个TA,且文献[11]中TAL包含的TA数超过上界。文献[12]则介绍了一种两步分配TAL框架,第1步是静态分配TA给TAL,第2步是根据UE的动态运动轨迹将TAL分配给UE。

第3类动态设计方法会根据不同的用户分配不同的TAL。触发用户进行TAU的阈值条件可以为距离、时间、速度等。文献[14-15]提出了一种一维TAL模型,研究当用户分别以不同的概率左移、右移到相邻小区时需要进行的TAU和呼叫总信令之和。这种方法只考虑到两种UE移动方向,不符合实际的UE运动轨迹,因此不能满足5G网络架构中总信令消耗研究。文献[16-17]使用二维TAL模型,设定TAL是由正六边形的小区环TA组成,并提出了种基于用户移动特征的TAL设计算法,使得TAU信令和呼叫信令最小。但这种方法设定一个TA中仅含一个小区,与实际的5G网络部署不符,因此存在局限性。

此外,文献[18]通过分析UE的运动特点来减少或者增加TA中包含的总小区数,且假设用户不经过环上的某些小区,因此TA不是以环为单位,而是以单个小区为单位。文献[19]提出了一种基于分布式小区的二维位置区域(location area, LA)规划算法,使得位置管理和寻呼过程的总信令最小。提出的算法在分析出大量UE运动轨迹后,规划出哪些小区属于相同的LA。在这一方案中,大量用户设备的运动轨迹数据很难收集也不便处理。文献[20]基于4G和5G网络中移动设备的历史通信参数记录,采用基因遗传算法和多目标算法来预测用户的速度以及可能的运动路径。机器学习算法复杂需要大量的真实数据,一旦预测错误,会带来更多的信令消耗。

为了解决以上问题,本文提出一种基于马尔可夫链的新型二维随机移动模型。相比于已有的模型,本文所提出的模型做了以下改进:

(1) 假设TAL中包含的TA数量可变,且最大值不能超过3GPP协议中规定的数值。TA由多圈的正六边形同心小区环组成,且数量可变。

(2) 在构建TAL模型时,采用新型TA分组方式,将最外层TA分为内嵌TA和外临TA类型。在构建TA模型时,采用新型小区编号方式,并定义吸收态代表TA外部相邻小区。以马尔可夫链为基础预测用户从初始位置转移到不同类型TA后,在TA内部不同编号小区内随机移动结果。

(3) 通过大量的模型验证实验确定模型正确性,模拟用户在模型中转移数万步后停留的稳定状态,且由此分析单个UE的运动轨迹特征。

本文分析了TA半径,用户的移动速度以及进行单次TAU所消耗的信令和单次呼叫所消耗的信令对总信令消耗的影响。并通过模型构建找到参数不同的情况下,移动性管理中的信令消耗最小时的最优TAL配置。在最优TAL配置下,信令消耗减少,性能显著提升。

1 系统模型

1.1 小区、TA与TAL的结构

在个人通信系统(personal cornmunication system, PCS)系统中,要分析用户在移动性管理中的总信令消耗,需要对小区、TA以及TAL做模型假设。本文中构建的小区模型为正六边形,TA由多个正六边形小区组成,TAL中包含多个TA,且根据3GPP协议,一个TAL中包含的TA数量应该不大于16个,如图1所示。

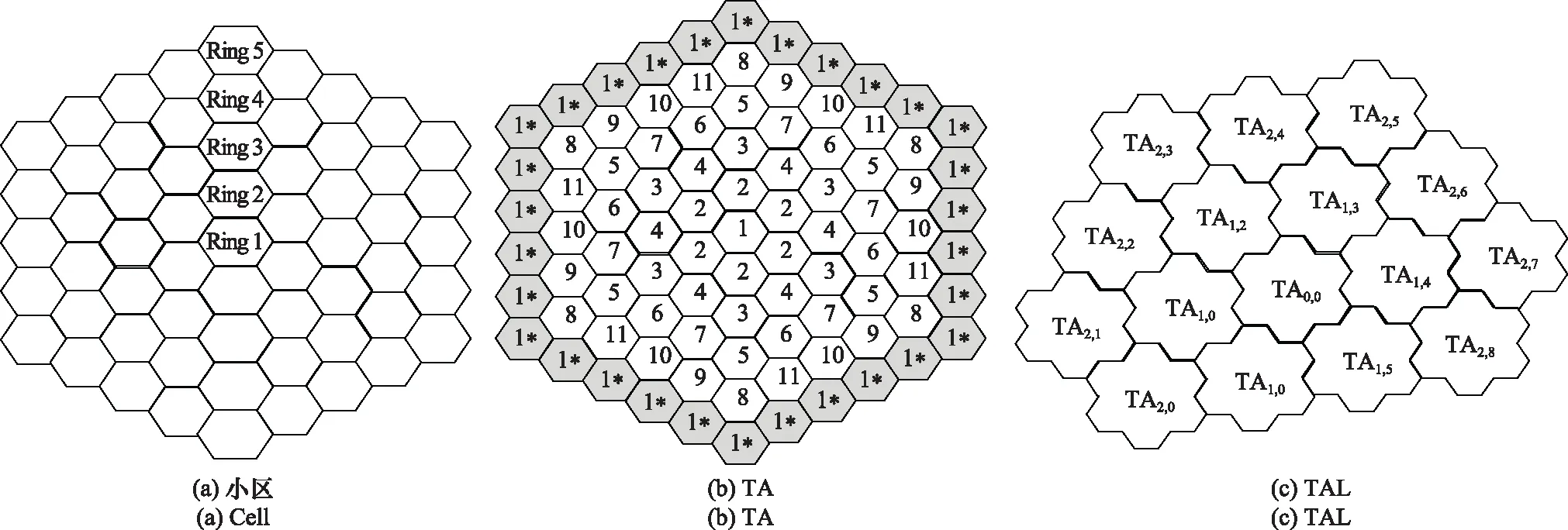
图1 小区、TA和TAL模型Fig.1 Cell, TA and TAL model

(1) 小区结构:假定在5G网络架构中,小区都是正六边形且每个小区都有6个相邻小区。因此,小区中的移动设备能以1/6的概率分别移动到相邻小区。

(2) TA结构:假定在5G架构中,TA包含相同小区形状的环状结构。用表示TA的半径,则TA是由Ring 1,Ring 2,…,Ring构成的。由图1(a)可以看出,Ring 1是中心环,且Ring 1包含一个小区,Ring 2包含6个小区,由此可以类推,每个环包含的小区个数为6(-1),因此TA中总的小区个数为3-3+1,图1(a)中TA的半径为5,包含的总小区数为61。分析用户的移动方向,要对小区进行编号,如图1(b)所示。

从中心Ring 1开始,Ring 1中只包含一个小区,将小区编号为1。

向外层扩展到Ring 2,从Ring 2的转角位置开始,将小区编号为2,由图1(b)中可以看出,Ring 2有6个转角位置,因此Ring 2中所有的小区都为编号2。

向外层扩展到Ring 3,从六边形环的转角位置开始,将小区编号为3。按照顺时针方向移动,依次增加小区的编号直到下一个转角为止,依次给小区编号为3和4,剩余小区也按照相同的方式进行编号。

向外层扩展到Ring 4,从六边形的转角位置开始,将小区编号为5。按照顺时针方向移动。

按照步骤2～步骤4同样的方式对剩下的环进行编号。

与最外层相邻的阴影部分环标号为1*,表示用户离开TA之后进入吸收态。由此完成对小区的编号。

(3) TAL结构:本文中构建的TAL是由一个位于中心的TA以及周围的同心环状TA构成,在TAL列表中所有TA的包含小区个数是相同的。由于TAL中包含的TA最大数量为16,因此TAL最多由3层环构成。用表示TAL中的TA个数,当1<≤7时,TAL只由Ring 0和Ring 1构成,Ring 1包含的TA个数为-1。当7<≤16时,TAL由Ring 0、Ring 1和Ring 2构成,分别包含的TA个数为1、6和-7。已有的研究表明,TAL中包含的TA个数并不是影响信令消耗的关键因素。因此，在本文中,设定TAL中包含16个TA,如图1(c)所示。用TA,对不同位置的TA进行标识,其中表示环编号,表示同环中的小区编号,且编号规则如下:

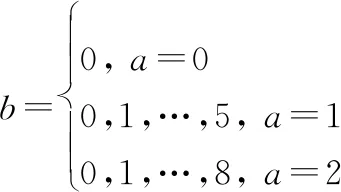
(1)

设定TA是UE最近一次进行TAU的区域。为了方便数学分析,TAL中边境区域的TA可以分为两种类型,内嵌TA和外临TA。内嵌TA在同一个TAL中有4个相邻的TA,外临TA在同一个TAL中有3个相邻的TA。图1(c)中,TA,TA,TA,TA,TA,TA属于外临TA,TA,TA,TA,TA,TA属于内嵌TA,Ring 2中去掉了两个内嵌TA和一个外临TA。除此之外,还有另外一种组合方式,Ring 2中会去掉一个内嵌TA和两个外临TA,两种方式对总信令影响并没有太大差异。图1(c)中TAL中TA的形状会随着半径的增加而改变,具体变化方式如图1(b)所示。

1.2 流体模型

为了解决UE的小区穿过率问题,研究者们提出了一种流体模型。流体模型假设用户的速度服从独立同分布,运动方向范围为[0,2π),且UE在小区中是均匀分布的。用CR表示用户的边境穿过率,推导公式如下:

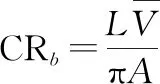
(2)

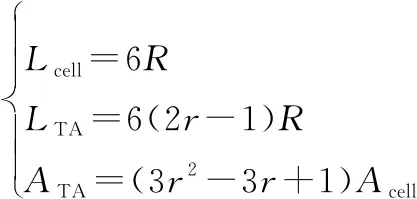
用表示用户离开当前小区仍然处于同一个TA的概率,用,分别表示TA驻留时间和小区驻留时间,,都服从独立同分布,且1,1分别表示、的平均值。关系为

=(1-)

(3)

由式(2)和式(3)得

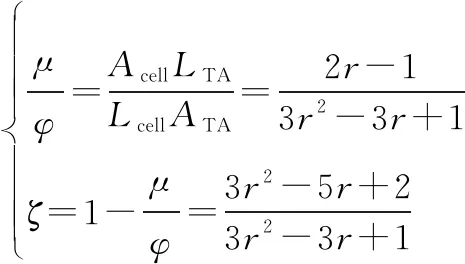
(4)

1.3 呼叫模型

在PCS系统中为了降低寻呼信令消耗,采用的寻呼方案有轮询法、连续呼叫法和基于用户速度和距离大小采用的寻呼方案等。轮询呼叫方案中,当用户接收到寻呼之后,呼叫区中所有的小区都会被同时呼叫,因此不会存在延时等问题。连续呼叫方案中,寻呼区域会被划分成几个相邻的寻呼区,当用户接收到寻呼之后,基站会分别在这些划分之后的寻呼区接连发起呼叫,直到找到被呼叫的用户为止。本文中选用的呼叫方案为平行呼叫方案,通信系统的呼叫间隔服从泊松分布,呼叫率为。因此呼叫间隔t服从指数分布,平均值为1/。

1.4 二维随机移动模型

处于小区中的所有用户在TAL中的运动模式都是相同的,本文中选取的二维随机模型中,用户的TA驻留时间服从独立同分布。用户离开TA后会以1/6的同等概率转移到相邻的6个TA。用户在离开内嵌TA后会有1/3的概率转出当前TAL,在离开外临TA后会有1/2的概率转出当前TAL。且在TA模型中,用户转移到具体TA某小区后,会以1/6的同等概率转移到相邻的6个小区。

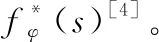
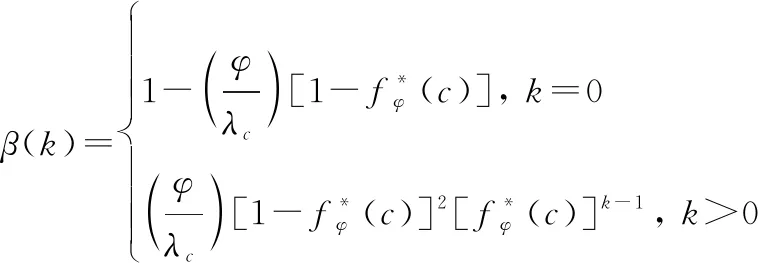
(5)

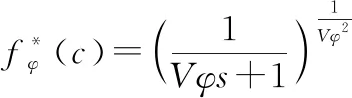
(6)

2 模型分析

本文以马尔可夫链为基础预测用户在TAL中随机移动的位置,在第2.1节和第2.2节中将会分析用户从中心TA转移到边界TA的概率,以及用户转移到边界TA中小区之后,从TA中边界小区转移出TAL的概率。

2.1 TAL的马尔可夫链分析

在本文中使用状态,代表用户当前处于TAL中TA,的位置,当用户发生TAU之后,状态会转到。本文中选取TAL的大小=16,对于其他大小的TAL分析方法仍然相同。因此马尔可夫链的状态空间如下所示:

={,,,,,,,,

,,,,,,,}

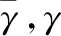
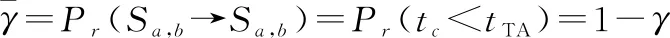
(7)

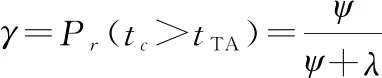
(8)

式中:表示用户收到呼叫的时间间隔;表示用户在TA中停留的时间间隔。当用户进入一个新的TA后有两种情况,一种情况是用户仍处于同一个TAL中,用μ表示用户进入新TA后仍处于同一个TAL的转移概率

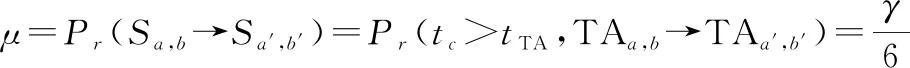
(9)

另一种情况是用户转到一个新的TAL,因此会发生TAU,用户状态从,变成。当用户处于内嵌TA时,用表示转移到不同TAL的概率:

(10)

当用户处于外临TA时,用表示转移到不同TAL的概率:

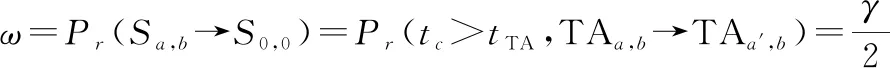
(11)

用表示用户在同一TAL内在不同TA间的马尔可夫转移矩阵,的矩阵表达式如下所示:

用表示马尔可夫链状态转移矩阵的平稳分布,则满足如下表达式:

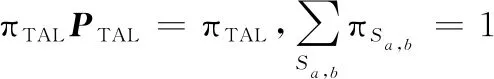
(12)

式中：π,表示用户处于状态,时的平稳分布。

那么由于用户穿出TAL,而发生TAU的平均次数为

NU=(π+π+π+π+π)+

(π+π+π+π+π+π)

(13)

穿出TAL之后用户的状态转为。

用表示用户在某一状态,停留的时间,本文模型中用户在接收到呼叫和穿出TAL都会发生状态变化。当呼叫间隔大于TA停留时间时,的值为。反之,的值为。因此两个连续状态变化的时间期望值表达式为

(14)

则单位时间内发生TAU平均次数为

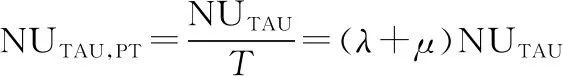
(15)

在两个呼叫间隔之间发生的TAU次数期望值为

(16)

2.2 TA中的马尔可夫链分析

TAL中所有的TA结构都相同,且包含相同的小区数量,按照系统模型的方式进行编号后,用户在半径为的TA中以及相邻TA对应的马尔可夫链转移矩阵如下:

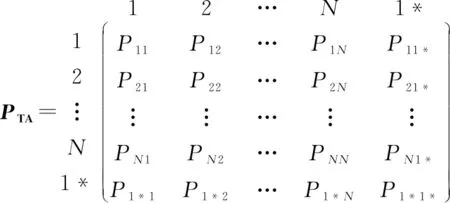
式中:1,2,…,为同一TA内小区编号;1*为用户转到相邻TA内小区的吸收态。马尔可夫链转移矩阵可由状态转移图得到。

用户在半径为5的TA内,各小区之间的状态转移图如图2(a)所示,共有11种状态,图中未做特别标识的转移概率都为1/6。边界小区与相邻TA中定义的吸收态之间的转移图如图2(b)所示,半径为5的TA边界小区编号分别为8,9,10,11,其中1*为转到相邻小区的吸收态。由可得用户在TA内的一步转移概率,那么用户在TA内的步转移概率为

(17)

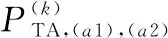
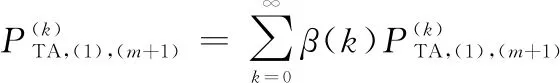
(18)

式中:(+1)为吸收态小区编号;()为第14节中用户在TA内转移步的概率。

用户在同一TAL列表中转移到边界的内嵌TA和外临TA后,进入TA中小区,用户在TA中随机移动步之后,由于转出TAL而进行的TAU信令数学期望表达式为

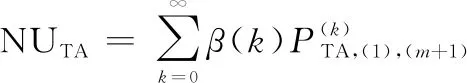
(19)

2.3 呼叫模型分析

本文中选取的呼叫模型为平行呼叫,因此用户在TAL内被寻呼时,用表示接收到寻呼指令的小区个数,表达式为

NU=16(3-3+1)

(20)

2.4 总信令消耗分析

用户在两个呼叫间隔之间由于发生TAU和寻呼所消耗的总信令表达式为

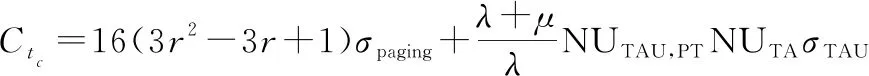
(21)

式中:和分别表示进行寻呼时以及进行TAU时所消耗的信令。

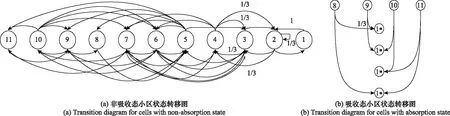
图2 半径为5的 TA内状态转移图Fig.2 Transition diagram for a TA with radius is 5

3 模型验证

本节中通过蒙特卡罗仿真法以及Matlab平台来验证TAL模型,TA模型以及整体模型的正确性。由于在TA和TAL中用户的二维随机移动模型具有随机性,因此可以直接对该模型进行蒙特卡罗模拟。通过随机生成的大量点数来模拟很多个UE在TAL以及TA中的移动情况,计算用户在不同的小区半径下移动到边界的总个数,由此模拟出用户出TAL以及TA边界的概率。验证过程中共重复该过程M1次,得到模拟结果的均值:

(22)

本节主要分别介绍TAL、TA以及整体模型的验证算法,模拟结果和分析结果数据值对比,从而验证模型的正确性。

3.1 TAL模型验证

如图1(c)所示,用户从初始位置TA出发,可分别从上、下、左上、左下、右上、右下方向转移到相邻TA,以及停留在原始TA。用生成的随机数分别模拟用户移动的移动方向,从而计算出用户转移到内嵌TA和外临TA的概率。用生成的随机数模拟用户在TAL中的移动路径流程如图3所示。

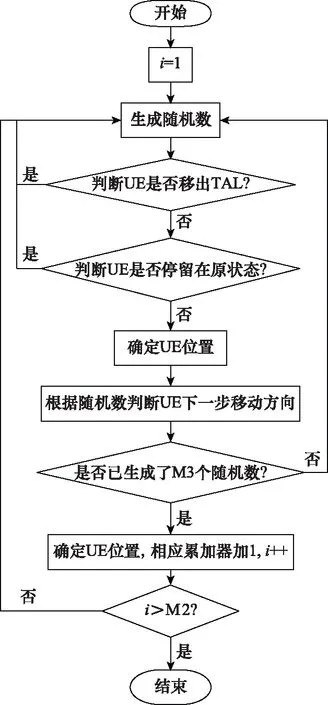
图3 TAL模拟流程Fig.3 TAL simulation procedure

生成M2个数模拟M2个UE在TAL内随机移动,对于每一个UE生成M3个随机数模拟用户的沿不同方向共移动M3次,本节中设M2和M3的值为10 000。UE处于TA和内层TA时有6个随机移动方向,处于内嵌TA时有4个随机移动方向,处于外临TA时有3个随机移动方向。当有6个随机移动方向时,分别用(0～1/6),(1/6～1/3),(1/3～1/2),(1/2～2/3),(2/3～5/6),(5/6～1)范围内的数对应6个不同的移动方向。相应地当UE所处的位置有4个移动方向和3个移动方向时,表示方法同理。

首先,根据生成随机数确定用户移动方向,之后判断用户是否移出TAL,如果移出TAL则不用做任何操作,因此在流程图中并未表示出。如果未移出TAL,则要判断用户是否还停留在原状态,如果UE还停留在原状态,则要根据下一次生成的随机数判断UE的下一步移动位置,如果UE未停留在原状态,则要确定UE转移到具体哪个TA,而后再根据随机数确定UE的下一步移动位置,如此生成M3个随机数,表示UE在TAL内移动了M3步,确定UE最后停留的位置,相应TA的累加器加1。如此重复M2次表示共有M2个UE在TAL中随机移动。最后由各TA对应累加器的值与M2的比值即表示UE停留在各TA的概率。

表1为=16时,TAL模型模拟结果、理论分析结果及误差率。TA的类型分为4种,即TA、内层TA、内嵌TA和外临TA。状态TA是指用户跨出TAL后,状态转移为TA,以及停留TA两种情况。状态为内层TA时,用户经过转移后最终停留在TA、TA、TA、TA。状态为内嵌TA和外临TA如第1.1节中TAL所述。

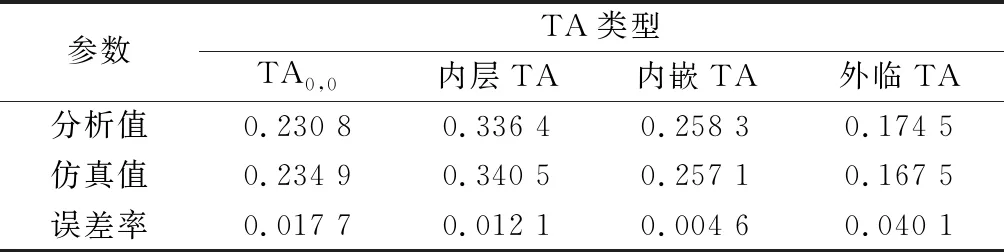
表1 UE转移到各TA的分析值与仿真值对比

从表1可以看出用户在TAL中随机移动停留在各类型TA的理论分析值以及模拟仿真值。用蒙特卡罗模拟用户走完10 000步之后稳定的状态,走到边界TA即内嵌TA和外临TA的概率分别为0.257 1和0.167 5,与理论分析值的误差分别为0.004 6和0.040 1。

为了进一步验证模型的适用性,用相同的方法分别模拟=4,7,10时,TAL模型的模拟结果和理论分析结果。

从表2可以看出,当取值不同时,用户转移到不同TA理论值与分析值误差均低于0.8%。进一步验证了对于不同,模型仍然适用。

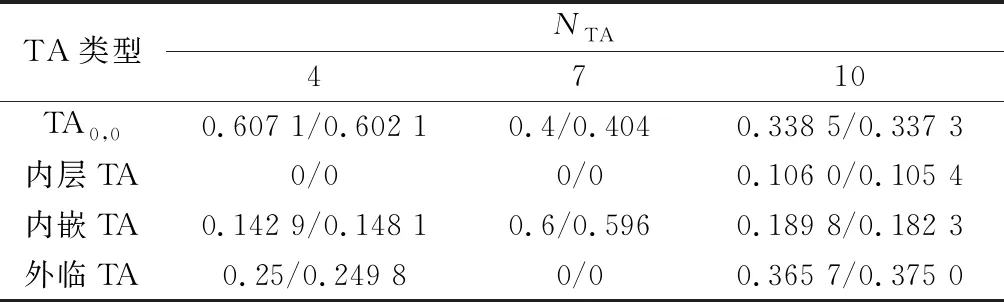
表2 不同NTA中UE转移到各TA分析值与仿真值对比

3.2 TA模型验证

本文构建的TA模型中,TA半径范围可从1增加到无穷大,因此本文在验证正确性时,需验证半径不停改变过程中,模拟用户穿过TA的概率。且在TA半径相同时,用户的移动速度不同也会导致穿出TA的概率不同。本节设定用户在小区停留时间均值与呼叫间隔比值。为10,用以表示用户的移动速度,详细的验证流程如图4所示。

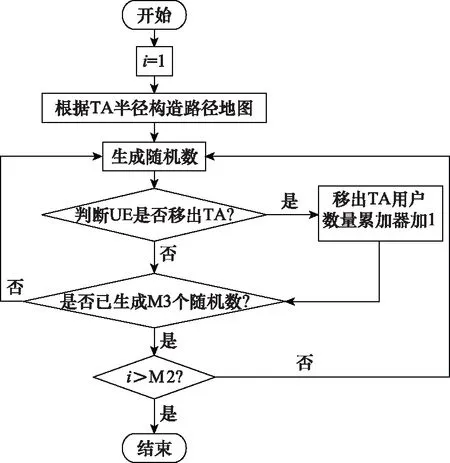
图4 TA模拟流程图Fig.4 TA simulation procedure

首先根据不同的TA半径构造出不同的路径地图,相应地为小区编号,TA外相邻小区编号为(+1)。对于单个UE,生成M3个随机数模拟用户在TAL中共移动M3步,TA中共有M2个用户。用生成的随机数模拟用户分别向6个方向随机移动,分别用(0～1/6),(1/6～1/3),(1/3～1/2),(1/2～2/3),(2/3～5/6),(5/6～1)范围内的数对应6个不同的移动方向。根据UE的移动方向,判断UE是否移出TA,移出的条件为UE所在位置的小区编号为(+1),移出TA则用户数量累加器加1。如此重复M2次,用移出TA的总用户数比M2表示移出TA概率的仿真值。

图5为模拟100个用户在半径从1变化到30的TA中随机移动模型,用户移出TA的概率理论值与分析值对比图。

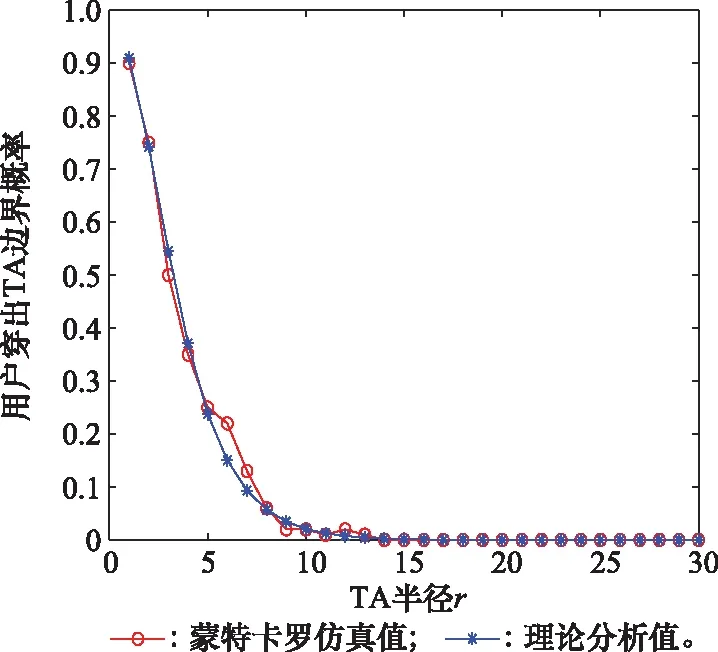
图5 100个UE在TA内移动对比Fig.5 Comparison between simulation and analysis for 100 UEs in TA

从图5可以看出,理论值与分析值曲线基本符合,但是由于样本数量不够大,不能模拟用户在TA中移动足够多步数后稳定的状态,而理论分析值最终计算的结果是转移矩阵对应的稳态分布,因此在TA半径为4和5时,两者存在较大误差。图6为模拟10 000个用户在半径从1变化到30的TA中随机移动模型,用户移出TA的概率理论值与分析值对比图。

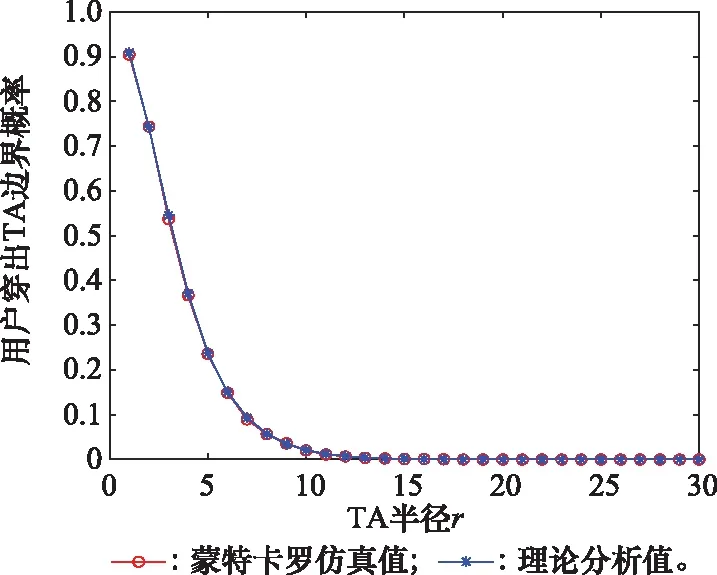
图6 10 000个UE在TA内移动对比Fig.6 Comparison between simulation and analysis for 10 000 UEs in TA

从图6可以看出,理论值与分析值曲线完全符合,当模拟足够多的UE在TA中移动,最终穿出TA的UE个数会达到稳定。表3为TA半径为5到9,UE穿出TA概率理论值、分析值以及误差率。

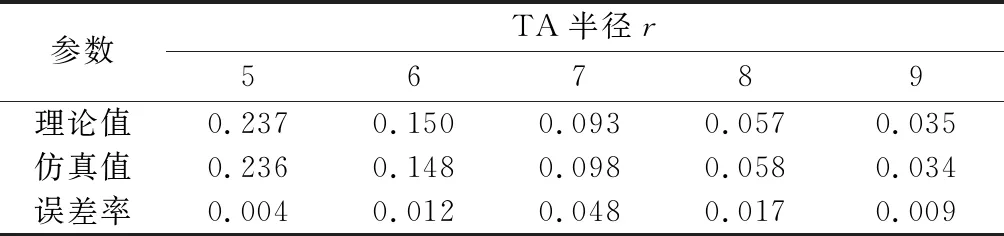
表3 UE转出TA概率分析值与理论值对比

表3为用户移动速度为10时,UE转出TA概率分析值与理论值对比,可以看出,用户在TA半径不同时,转出TA的概率分析值与理论值误差率稳定在小于0.05的范围,因此验证了模型的正确性。

3.3 整体模型验证

本节将验证TAL模型和TA模型结合之后的正确性。生成的大量随机数模拟用户从最初停留在TA,穿过TA内小区进入相邻TA,并穿过相邻TA中小区,最终因穿出整个TAL而进行的TAU信令消耗。

如表4所示,TA半径分别为5,6,7,8,9时,UE以φ/λ为10的速度从TA出发,从TAU的信令消耗理论值与分析值对比,可以看出误差率基本稳定在0.05左右,因此验证了整体模型的正确性。

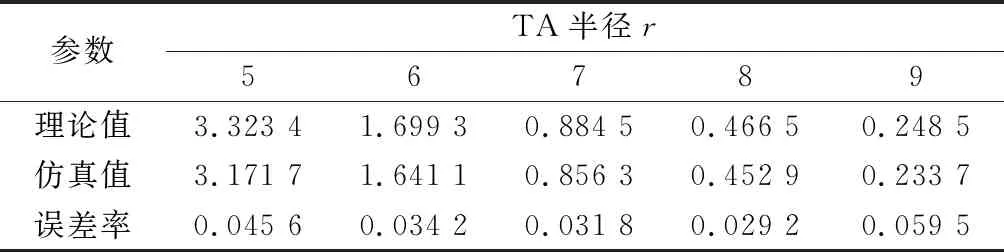
表4 整体模型信令消耗分析值与理论值对比

4 仿真分析

本节中分析了不同的参数对总信令消耗的影响,主要研究了TA的半径,用户的移动速度,进行TAU时的信令消耗和进行呼叫时的信令消耗对总信令消耗的影响。

图7为=1,=20的前提下,TA半径、用户移动速度对TAU信令消耗的影响。TAU信令消耗与TA半径呈现反比,当为1时,代表一个TA中只有一个小区,用户很容易穿出整个TAL。随着TA半径增大,一个TA中包含的小区从1增加到7,19,37等,用户穿出TAL的概率变小,因此由于TAU消耗信令变少。用户的移动速度对TAU信令消耗也有重大影响,图7中列举了用户速度分别为100,50,25时,TAU信令消耗的趋势变化图。在TA半径相同时,用户的移动速度越快,穿出TAL的概率越大,TAU信令消耗越大。

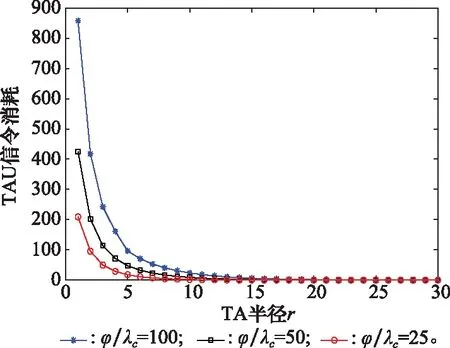
图7 速度对TAU信令消耗影响Fig.7 TAU signaling cost for various speeds

图8为=1,=20的前提下,TA半径、用户移动速度对总信令消耗的影响。由于总信令消耗包含寻呼信令消耗和TAU信令消耗两部分,而寻呼信令消耗与包含的小区个数呈现正向线性关系,TAU信令消耗与小区个数关系如图7所示。当包含小区个数较少时,总信令消耗主要受TAU信令消耗影响,当包含小区个数较多时,总信令消耗主要受寻呼信令消耗影响。图8中,TA半径增加到6时,总信令消耗基本不受TAU信令消耗影响。

图8 速度对总信令消耗影响Fig.8 Total signaling cost for various speeds

图9为=1,=20,用户的移动速度=50的前提下,TA半径对TAU信令消耗、寻呼信令消耗以及总信令消耗的影响。

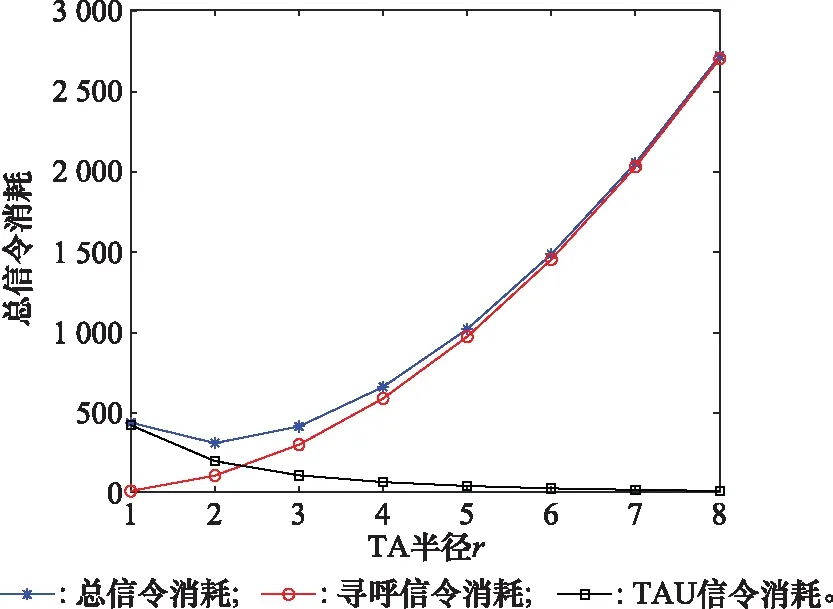
图9 TA半径对各信令消耗影响Fig.9 Different signaling cost versus TA radius

可以看出:① 当TA半径不停增大时,寻呼指令与半径呈现正相关,且增长速率越来越大,这是由于TA半径每增加1,TA中相应的小区增加6,用户收到寻呼指令时,基站会对TAL中所有小区发起广播。② 随着TA半径增大,总信令消耗先是呈现下降的趋势,下降到一定的值后开始上升,原因在于TAU信令消耗与呈现负相关,而寻呼指令消耗与呈现正相关。因此, 存在一个最优的TA半径,满足:

()+()<()+()

(23)

如图9所示,最优的TA半径=2。为了更直观展示和对总信令消耗影响,如图10所示,设=500,TA半径从1变化到10的前提下,和对总信令消耗的影响。

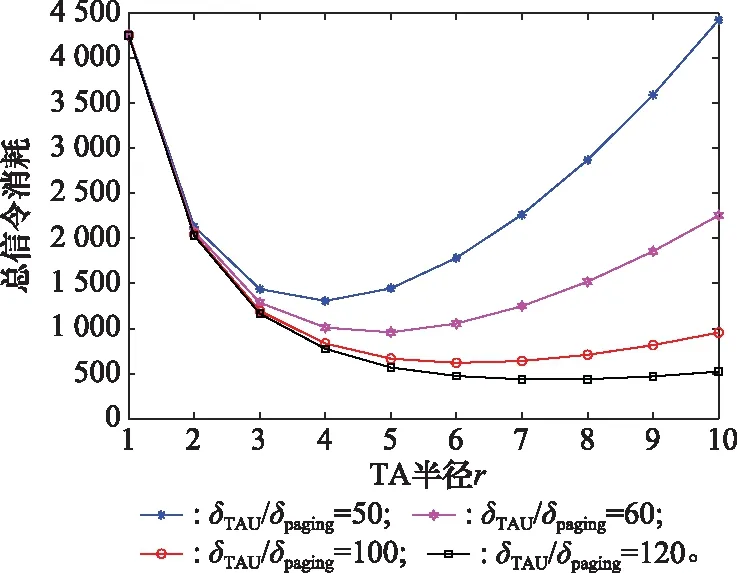
图10 δTAU和δpaging比值对总信令消耗影响Fig.10 Different signaling cost versus δTAU and δpaging radius

在和比值变化的情况下,TA的最优半径也会有所变化。由图10可以看出,/的比值分别为50,60,100,120时,对应的最优TA半径分别是4,5,6,7。原因在于/的值越大,在其他参数相同的情况下,由于进行TAU所消耗的信令越多,此时对应的TA半径越大用户越不容易穿过TAL,进行TAU消耗的信令越少。

图11为设=1,=20,用户的移动速度=50的前提下,TAL中包含的TA个数对总信令消耗的影响。

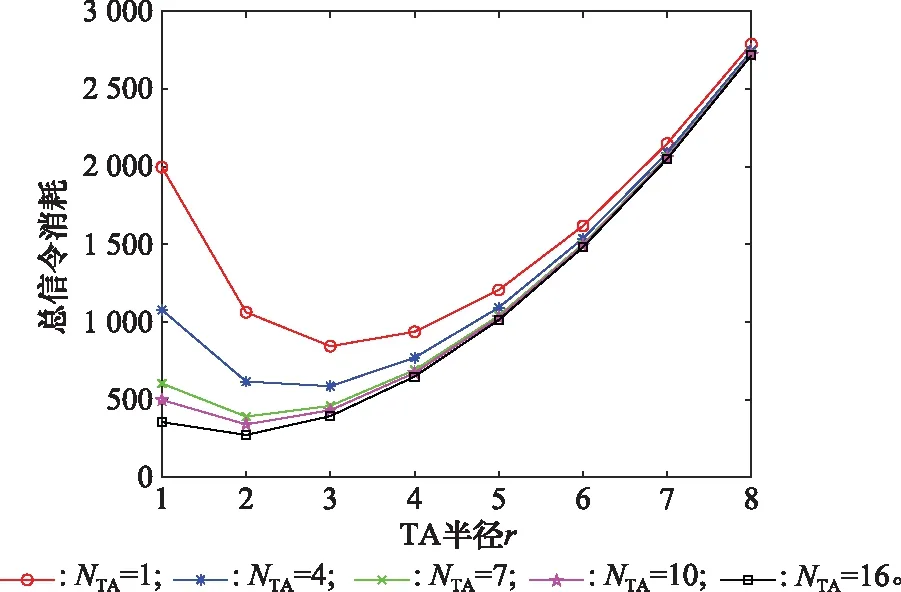
图11 NTA对总信令消耗影响Fig.11 Total signaling cost for various NTA

由图11可以看出,TA半径小于4时,的值越大,所消耗的总信令越少,原因在于越小时,总信令消耗主要受TAU影响,TAL中包含的TA数越多,用户越难穿出TAL,进行TAU的概率越小。因此,=1时,总信令消耗值最大,=16时,总信令消耗值最小。当值不同时,信令消耗最小时对应的最优半径不同,但相应的总信令消耗趋势都是先减少再增加,因此取16外的其他数值时,分析方法同=16相同。

5 结束语

本文的主要目的是通过找到最优的TAL分配模型来减少移动性管理中的信令消耗,分析了TA半径,用户的移动速度以及进行单次TAU所消耗的信令和单次呼叫所消耗的信令对总信令消耗的影响。相比于其他移动性管理方案,本文提出的基于马尔可夫链的二维随机移动模型优点在于不用收集大量的用户实际移动轨迹数据,具有可实践性高,易于操作等特点。缺点在于只考虑了一种平行寻呼方案,在确定TA半径时可能有所局限。未来研究可能会多结合一些寻呼方案,确定具体情形下的最优TAL分配。