三维非线性预设性能制导律设计

唐 骁, 叶继坤, 李 旭

(空军工程大学防空反导学院, 陕西 西安 710051)

0 引 言

在对高速机动目标拦截的末制导段,常把导弹与机动目标之间的最终脱靶距离作为设计制导律的一个重要指标。除此之外,还要实现对目标的直接碰撞拦截,这就要求拦截弹以特定的攻击角度攻击目标,以提高直接碰撞的成功率,所以需要设计出满足攻击角约束的三维制导律。

在对满足攻击角约束的制导律的研究中通常把攻击角约束转化为相应的终端视线角约束，因为滑模控制对系统不确定性具有鲁棒性和易于实现的特点,许多具有终端视线角约束的制导律都是基于滑模控制来设计的。基于滑模控制的制导律设计包括两个部分:滑模面的设计和趋近律的设计,设计滑模面来保证构成滑模面的各项可以收敛到预定的值,如系统状态和跟踪误差,滑模面的形式是多样的,常用的有线性滑模、非奇异终端滑模、积分滑模、分数阶滑模,滑模趋近律主要有等速趋近律、指数趋近律和一般趋近律,其目的是使滑模变量快速收敛以保证系统状态快速到达滑模面。

在滑模制导律的设计中,滑模变量的收敛性能可以通过调整趋近律的参数实现,但是基于李雅普诺夫理论和有限时间收敛理论设计的趋近律在不同拦截条件下同一组参数无法保证同样的收敛效果,找到合适的参数来保证滑模变量的瞬态收敛性能并不容易,特别是在末制导开始的阶段。

近年来,预设性能控制(prescribed performance control, PPC)已被广泛应用于制导控制系统设计中,文献[14]利用预设性能方法将航天器姿态跟踪误差限制在预设范围内,文献[15]针对高超声速飞行器高度控制提出PPC方法,保证了期望的动态性能和稳态精度。

基于PPC理论,跟踪误差可以按性能函数预先定义的收敛范围去收敛,为误差收敛的瞬态与稳态性能提供了一种简便的方法,本文将一种改进的性能函数应用于具有视线角约束的三维制导律设计中,使滑模变量按预设性能收敛。

为了提高制导律在实际应用中的性能,设计了有限时间观测器,结合微分跟踪器,在存在测量噪声的情况下精确估计目标信息,补偿制导律中由目标加速度引起的不确定项,保证制导律的有效执行。

本文首先建立了视线坐标系和三维拦截模型。然后,介绍了PPC理论,并给出所使用的性能函数形式。其次,详细推导了预设性能制导律(prescribed performance control guidance law, PPCG),分析制导律的稳定性。最后,介绍了干扰观测,并进行了数值仿真。

1 三维空间内弹目相对运动模型

相对于二维弹目运动模型,三维弹目相对运动的描述需要建立更复杂的空间坐标系,如图1所示。

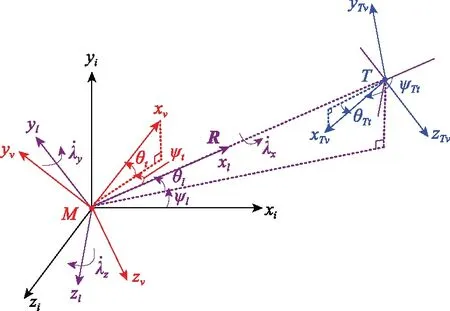
图1 三维弹目相对运动示意图Fig.1 Schematic diagram of three-dimensional relative motion of projectile

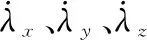
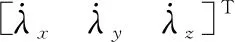
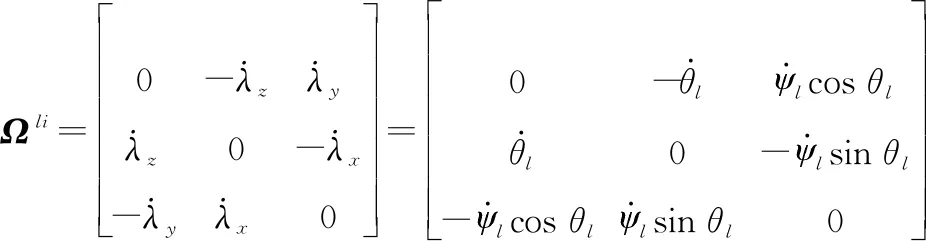
(1)

三维空间内描述导弹与目标相对运动的矢量方程如下:

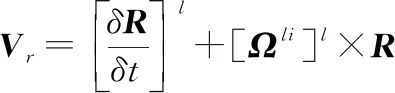
(2)

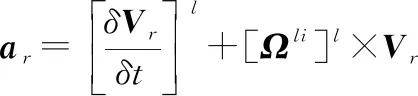
(3)

式中:和分别表示导弹与目标的速度与加速度矢量。对式在视线坐标系下投影可得

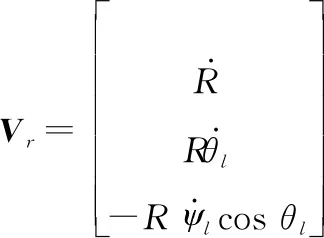
(4)

将式(4)代入式(3)可得到三维空间的弹目相对运动方程:

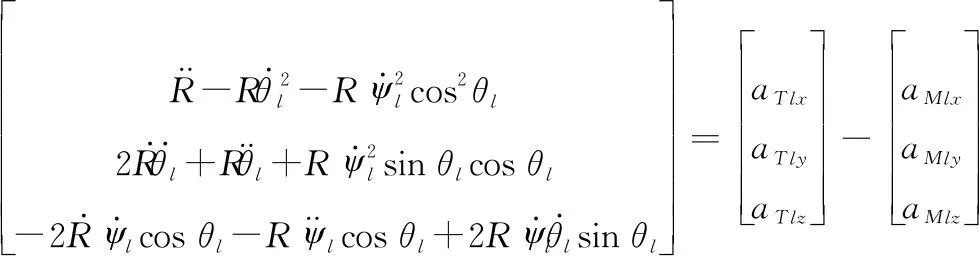
(5)

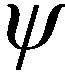
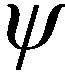
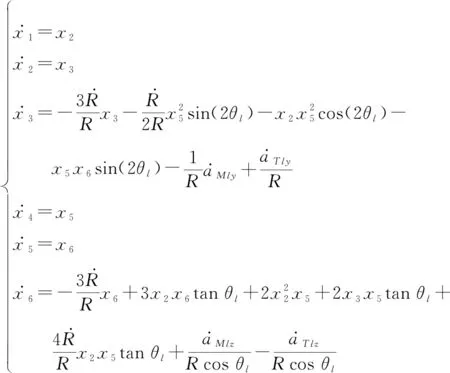
(6)

2 PPC基础理论

2.1 性能函数

通过引入性能函数,对跟踪误差()的瞬态和稳态性能进行设定,性能函数定义如下。

连续函数:→称为性能函数,满足:

(1)()是正的且严格递减;

在初始误差(0)已知的前提下,给出如下形式的不等式约束:

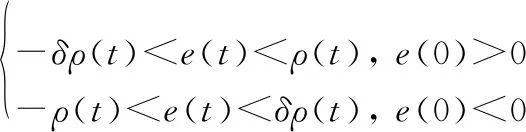
(7)

式中:∈[0,∞);∈[0,1]。

本文选取性能函数的形式为

()=(-)exp(-)+

(8)

如果不等式(7)成立,则误差曲线将被限制在-() 和()之间;另外,结合()的递减特性可知,误差()将在-() 和()的夹逼作用下迅速收敛到0的一个小领域内。常数表示预先设定的稳态误差上界,()的衰减速度为跟踪误差()收敛速度的下界,同时跟踪误差的最大超调量不会大于(0),因此可以通过选择适当的性能函数()和常数对跟踪误差的稳态和瞬态进行限制。

2.2 误差转换

在系统设计过程中,直接对不等式约束进行处理的难度非常大,均采用如下形式的误差变换函数(),将不等式约束转换为等式约束再进行处理,定义误差变换函数为

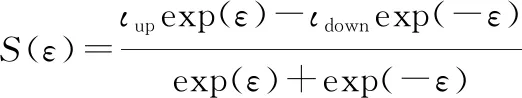
(9)

式中:,为设计的正常数。式(9)满足:

-<()<

(10)

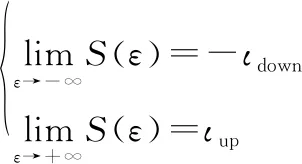
(11)

函数()除具有误差变换函数所要求的所有性质外,又因为∀∈(-∞,+∞),d()d>0是有界的,所以()是充分光滑的且严格单调递增有界。

跟踪误差和变换误差的关系可以表示为

()=()()

(12)

对误差变换函数()进行化简:

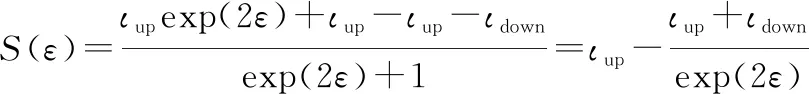
(13)

可以得到()的逆函数:

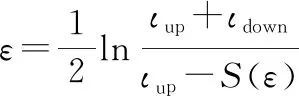
(14)

令=表示函数的逆函数,则式(12)可以等价表示为

=()

(15)

={∈∶-<()<}

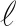
3 制导律设计

带攻击角度约束的三维PPCG分别在视线俯仰平面和视线偏航平面内设计滑模变量和:

=++

(16)

=++

(17)

式中:、、、分别为大于零的常数且满足Hurwitz稳定。当=0,=0成立时,、、、在有限时间内趋近于0。

3.1 视线俯仰平面制导律设计

在视线俯仰平面内设计制导律,针对滑模变量,设跟踪误差为=-0,对跟踪误差求导可得

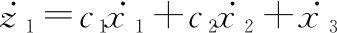
(18)

利用误差转换函数:

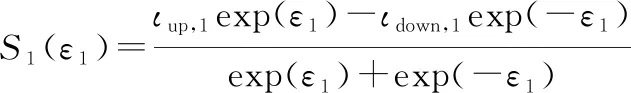
(19)

()=(-)exp(-)+

(20)

对进行误差转化,,为设计的正常数,为性能函数,、、为设计的正常数。

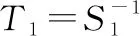
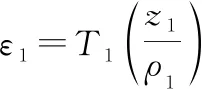
(21)

对式(21)两边对时间求导,得到

(22)

结合三维制导模型式(6)和转换后的误差方程式(22),可以得到视线俯仰平面内的制导系统模型为

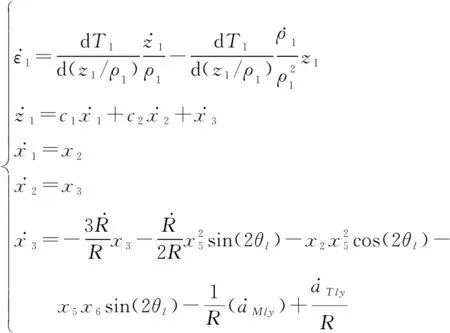
(23)

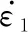
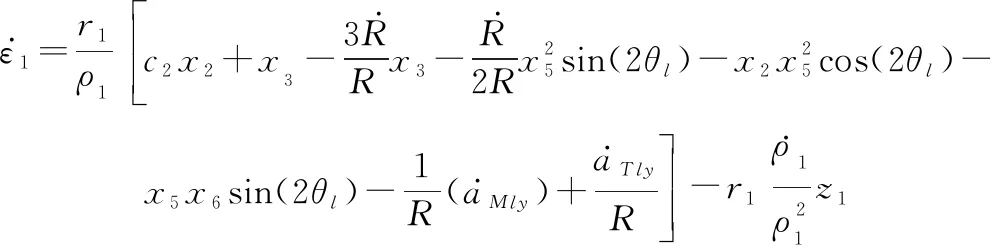
(24)

式中:=dd()>0;>0。

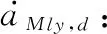
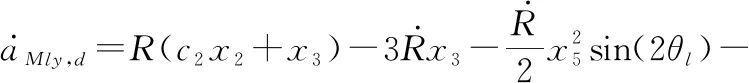
(25)

3.2 视线偏航平面制导律设计

在视线偏航平面内,针对滑模变量,设跟踪误差为=-0,对求导可得

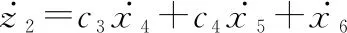
(26)

利用误差转换函数:

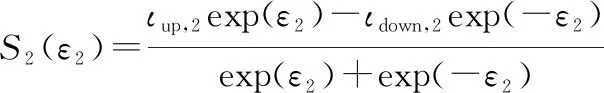
(27)

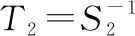
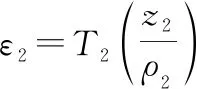
(28)

对式(28)两边对时间求导,得到

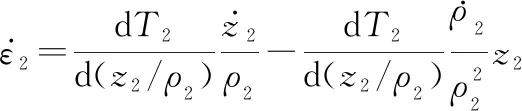
(29)

视线偏航平面内的制导系统模型为

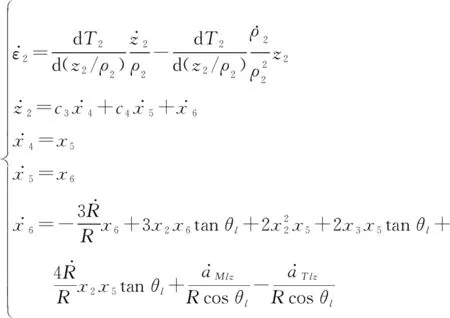
(30)

将式(26)代入式(29),得到

(31)

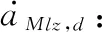
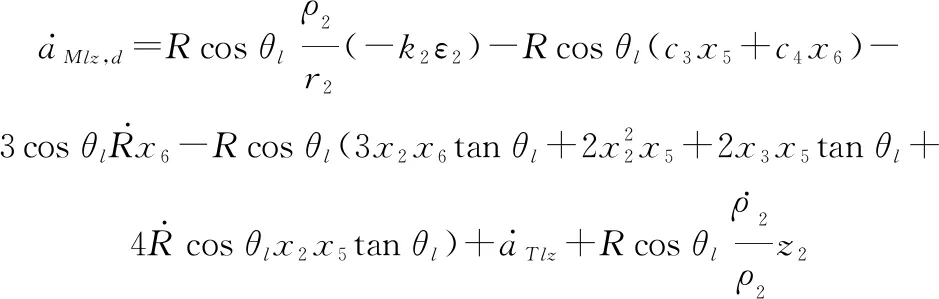
(32)

3.3 制导律稳定性证明

选取Lyapunov函数为

(33)

对式(33)两边对时间求导,得到

(34)

将式(24)和式(31)代入式(34),得到

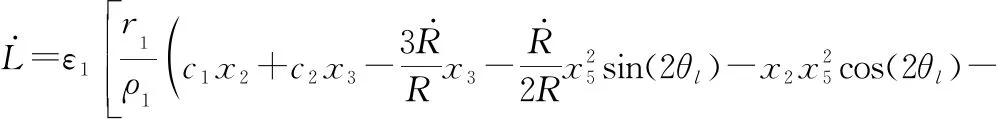
(35)

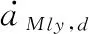
(36)

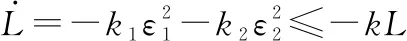
(37)

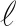
对于视线俯仰平面内,由于有界,所以由误差函数的性质可得误差状态量满足预设的瞬态和稳态性能,将在有限的时间内以预设性能收敛。

以此类推,对于在视线偏航平面内,有界,将在有限的时间内以预设性能收敛。

4 目标信息估计

在对目标的拦截过程中,导引头获取的目标信息有限且带有测量噪声,视线角的微分信号难以提取,目标加速度更无法测量,通常利用观测器进行估计。本文采用有限时间观测器进行估计,本节只给出视线俯仰平面中的有限时间观测器具体形式。

根据第1节给出的含攻击角度约束的制导模型:

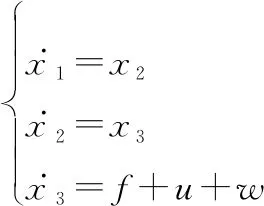
(38)

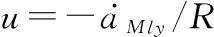
构建状态估计方程:

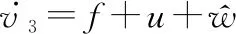
(39)

为的估计值,估计误差为

=-

(40)

构建终端滑模面:

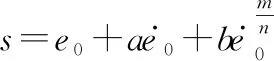
(41)

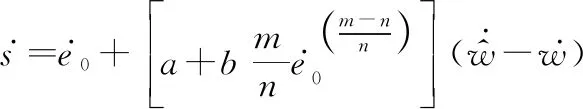
(42)

选择Lyapunov函数:

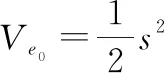
(43)

对式(43)求导可得

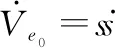
(44)

将式(41)、式(42)代入式(44)可得

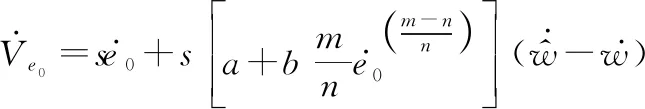
(45)

取扰动估计值为

(46)

代入式(45)可得

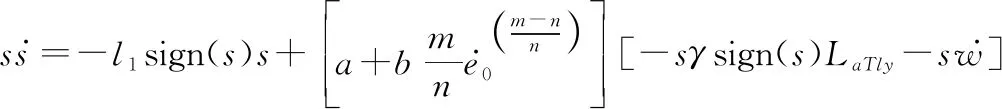
(47)

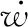
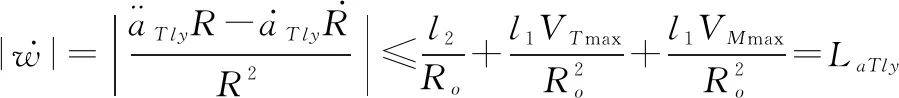
(48)

式中:>0,>0为目标加速度的上界;max、max分别为目标和导弹最大速度,弹目距离满足≥,为导引头盲区距离,在盲区内,导弹依靠惯性飞行,由此可得

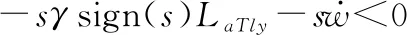
(49)

(50)

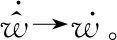
利用跟踪微分滤波器,可得滤波后的视线角速率以及视线角速率的微分信号:

(51)

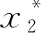
(52)

5 仿真分析

为验证PPCG的有效性,本节将设置目标圆弧机动和螺旋机动两种模式下对PPCG进行仿真;为了突出PPCG的特点,在相同仿真条件下与快速终端滑模制导律进行了对比,最后验证了有限时间观测器对目标信息的估计性能。

5.1 不同机动模式对比仿真

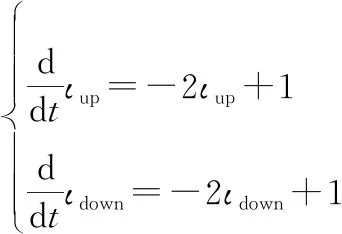
(53)

预设性能参数设置如表1所示。

表1 预设性能参数

目标在纵向和侧向平面分别做 =2, =2的圆弧机动,仿真结果如图2所示。

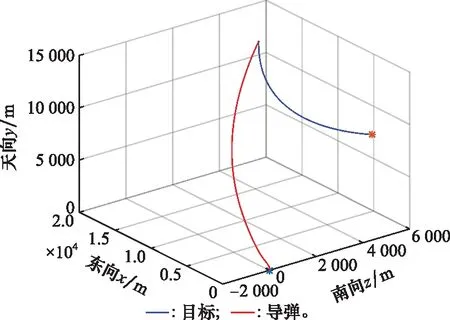
图2 圆弧机动弹道轨迹曲线Fig.2 Arc maneuver ballistic trajectory curve

仿真结果如图2～图7所示,整个拦截过程持续时间为21.515 s,最终脱靶量为0.018 m,说明本文所设计的三维PPCG能够满足对常值机动目标的精确打击需求。图4表示视线俯仰和视线偏航平面的滑模变量变化曲线,可以看出在PPCG的作用下滑模变量可以在预设性能范围内实现收敛,收敛时间约为2.8 s,滑模变量在收敛过程中变化平缓,且收敛之后能继续保持光滑且无抖振。由图5可以看出,视线俯仰和视线偏航平面内视线角速率的收敛特性与滑模变量基本一致。由图6可以看出,视线倾角和视线偏角都能在有限时间内收敛到期望值附近,满足拦截的末端视线角约束要求。图7为导弹在视线俯仰和视线偏航平面过载变化曲线,在制导初始阶段过载出现短暂的饱和,但随着滑模面的收敛,两个平面内的过载曲线也都快速收敛,这反映了PPCG在拦截机动目标时的有效性。

图3 圆弧机动弹目距离曲线Fig.3 Arc maneuver curve of projectile distance

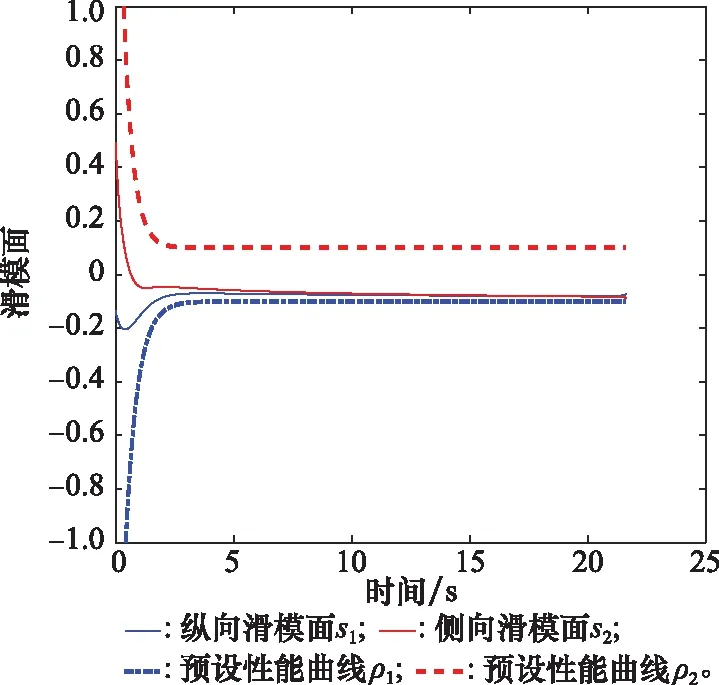
图4 圆弧机动滑模面变化曲线Fig.4 Arc maneuver change curve of sliding surface

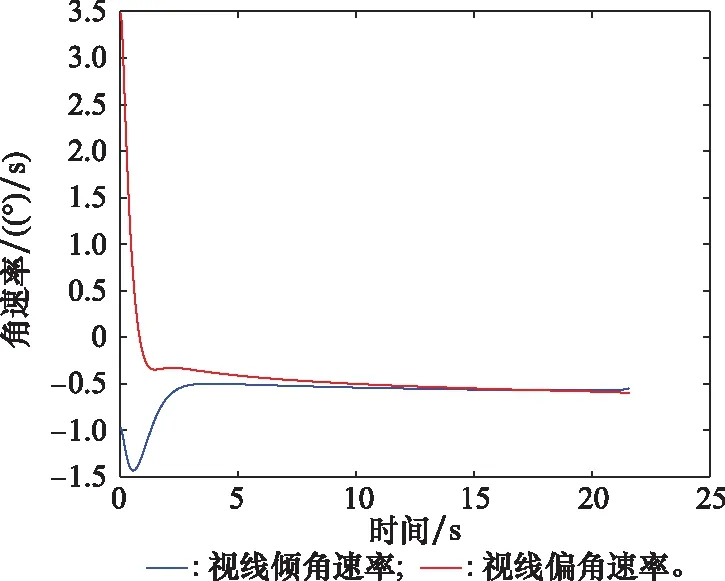
图5 圆弧机动视线角速率曲线Fig.5 Arc maneuver angular rate curve of line of sight

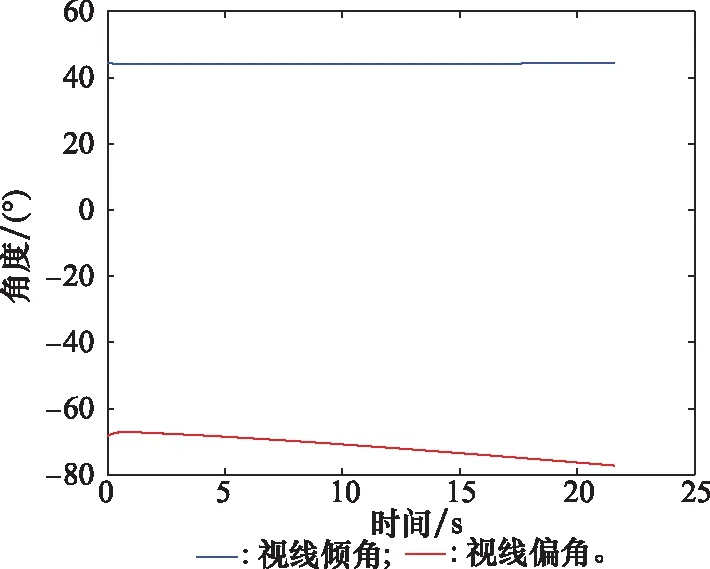
图6 圆弧机动视线角曲线Fig.6 Arc maneuver line of sight Angle curve

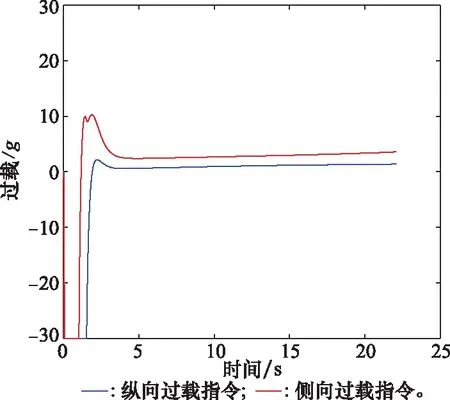
图7 圆弧机动导弹过载曲线Fig.7 Arc maneuver missile overload curve

目标在两个平面分别做 =5sin(π4), =5cos(π4)的螺旋机动。

图8～图12给出了三维空间中拦截螺旋机动目标的仿真曲线,拦截时间为16.183 s,命中目标时脱靶量为0.250 m,不难看出,在预设性能制导律的作用下,即使拦截螺旋机动目标,也能保证滑模变量在预设性能范围内收敛,同时也能使视线角收敛到期望值,视线俯仰和视线偏航平面的过载曲线也都快速跟踪上各自平面内的目标机动,体现了预设性能制导律良好的制导稳定性。

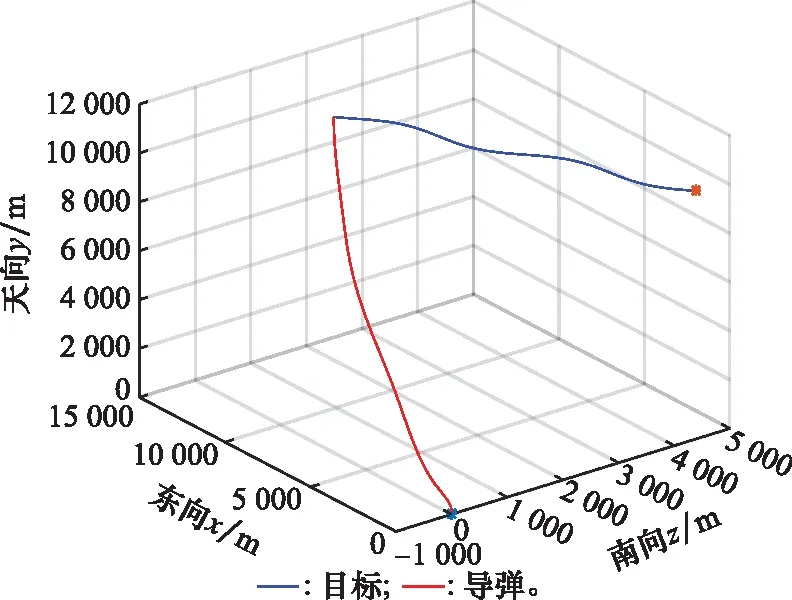
图8 螺旋机动弹道轨迹曲线Fig.8 Spiral maneuve ballistic trajectory curve

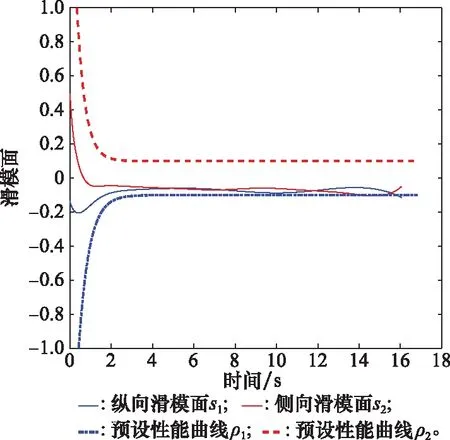
图9 螺旋机动滑模面变化曲线Fig.9 Spiral maneuve change curve of sliding surface

图10 螺旋机动视线角曲线Fig.10 Spiral maneuver line of sight Angle curve

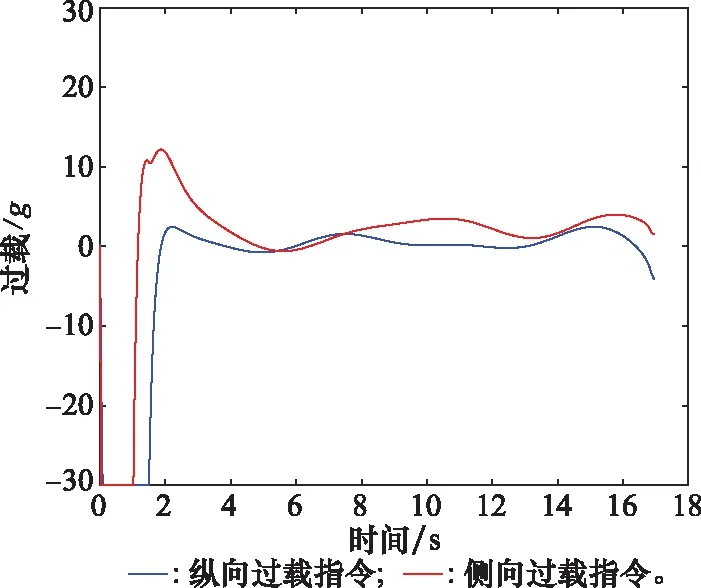
图11 螺旋机动导弹过载曲线Fig.11 Spiral maneuve missile overload curve

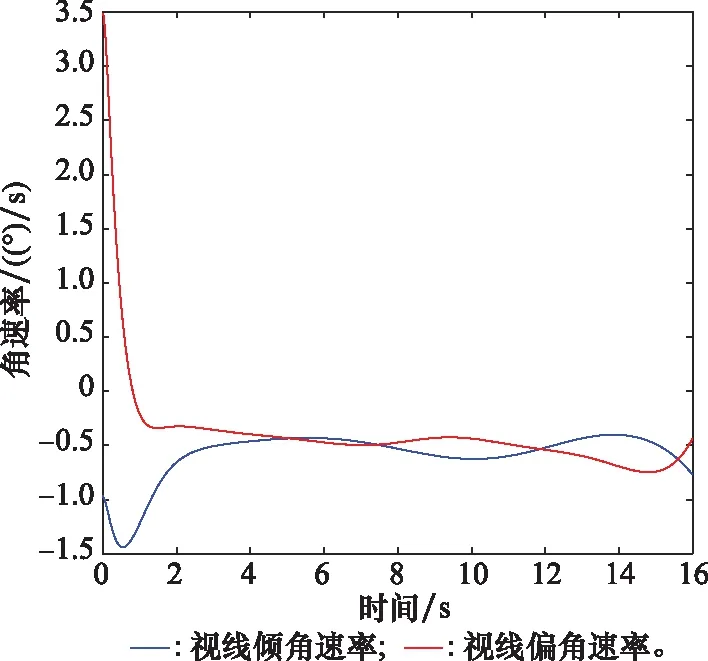
图12 螺旋机动视线角速率曲线Fig.12 Spiral maneuve angular rate curve of line of sight

5.2 不同制导律性能对比

为进一步说明本文设计的PPCG的优越性,将其与文献[22]提出的基于非奇异快速终端滑模和改进超螺旋算法的超螺旋终端滑模制导律(finite time superspiral sliding mode guidance law, FTSSMG)进行仿真对比,仿真条件同情境2,仿真结果如图13～图15所示。

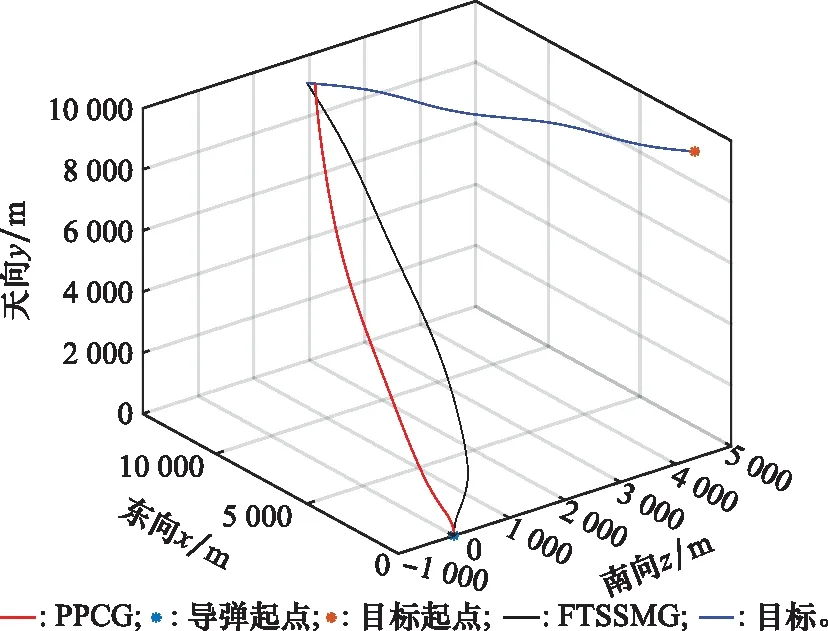
图13 弹道轨迹曲线对比Fig.13 Ballistic trajectory curve comparison

图14 导弹过载曲线对比Fig.14 Missile overload curve comparison

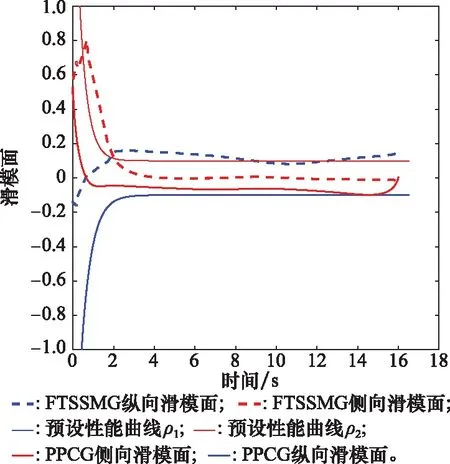
图15 滑模面变化曲线对此Fig.15 Change curve of sliding surface comparison

由仿真结果可以看出,整体而言,FTSSMG和PPCG都具有良好的有限时间收敛特性,拦截时间和脱靶量相差不大,能够满足机动目标拦截要求。但具体来看,FTSSMG的滑模变量收敛的暂态性能和稳态性能都不如PPCG, PPCG滑模变量按预设性能收敛,收敛精度要高于FTSSMG(见图15),在收敛速度方面,PPCG也要快于FTSSMG,FTSSMG在制导初始阶段的滑模变量变化和过载变化都不如PPCG平滑,FTSSMG的过载在正负饱和值之间出现跳变,而且饱和值持续时间更长,相比之下PPCG更有利于弹上执行。

5.3 目标信息估计仿真分析

为了验证第4节设计的有限时间观测器的有效性,给视线角速率加均方差为1.06×10rad/s的高斯白噪声,有限时间观测器参数设置为=3,=0005,=1,=01,=3,=5,其余仿真条件同情境2,由于仿真结果相似,因此这里仅给出视线角速率及目标加速度估计曲线,如图16和图17所示。

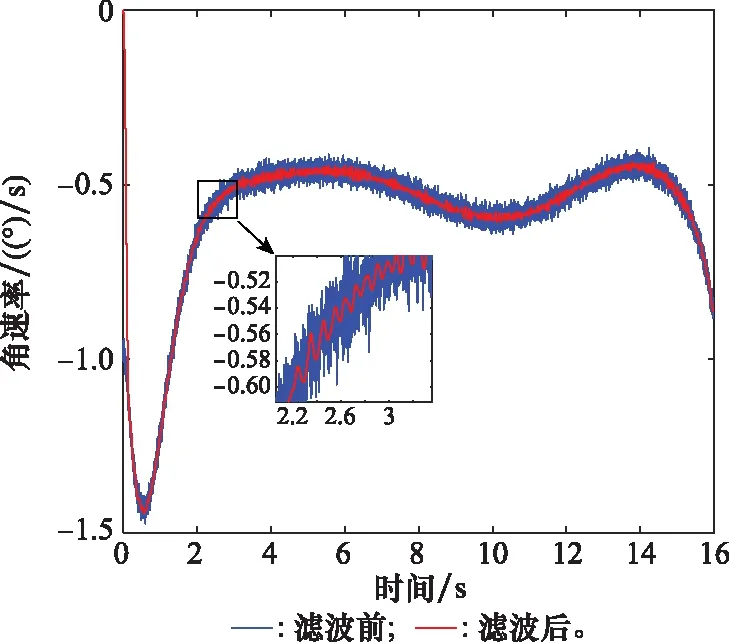
图16 目标螺旋机动视线角速率Fig.16 Angular line of sight rate of target spiral maneuver

图17 目标加速度估计曲线Fig.17 Estimation curve of target acceleration

由图18可知,估计误差能够在1.8 s内收敛,利用有限时间观测器输出的目标信息补偿PPCG中的不确定项,在有测量误差的情况下仍能成功拦截目标,目标做螺旋机动时的脱靶量为0.361 m,拦截时间为16.333 s。因此,有限时间观测器具有良好视线角速率滤波特性及不确定性补偿能力。

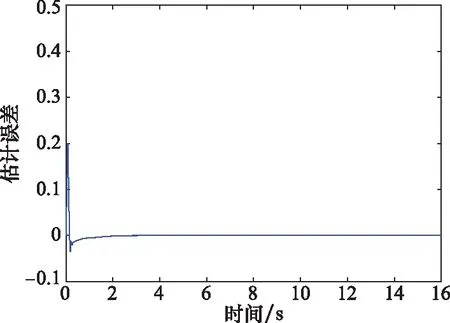
图18 估计误差曲线Fig.18 Estimation error curve

6 结 论

针对机动目标拦截攻击角度约束制导问题,本文基于预设性能控制理论,考虑三维空间内的耦合制导模型,提出一种三维PPCG,并基于二次型Lyapunov函数证明了稳定性。PPCG能够提高制导指令的瞬态性能,避免了过载剧烈变化;滑模变量的收敛参数可以根据预先设计的性能函数进行解析确定;同一组参数,在不同拦截条件下,滑模变量仍能达到规定的收敛效果。其次,PPCG的实现需要较多的弹目运动信息,为了提高目标拦截精度,提出了一种新的有限时间状态观测器来估计目标加速度并对滑模制导律进行补偿,用Lyapunov函数证明了观测器闭环系统的稳定性,仿真结果验证了所提方法的有效性。