融合深度图像先验的全变差图像着色算法

张 玺, 金正猛, 姜亚琴

(南京邮电大学理学院, 江苏 南京 210023)

0 引 言

图像着色是借助计算机技术将灰度图像转化为彩色图像的过程,目前广泛应用于广告、医疗、影视、古画修复等领域。传统的图像着色方法可以分为两类:一类是基于颜色转移的图像着色方法,另一类是基于颜色扩散的图像着色方法。基于颜色转移的图像着色方法需要用户首先输入一幅与目标灰度图像内容信息相近的彩色源图像,再通过合适的算法将源图像中的颜色转移到输入的灰度图像上,该方法的着色效果依赖于彩色源图像的选取。基于颜色扩散的图像着色方法需要人为地将部分颜色添加到目标灰度图像中,再利用适当的算法将所给的颜色信息扩散到整个灰度图像,该方法的着色效果依赖于人为添加的颜色。随着人工智能的快速发展,基于深度学习的图像着色方法已得到越来越广泛的应用,该方法利用在大量数据集下训练好的卷积神经网络,以端对端的方式直接对灰度图像进行着色,减少了人工参与,但其着色效果取决于网络本身的设计和训练集的选取。

近20年来,基于变分偏微分方程的颜色扩散着色方法已得到广泛研究。Sapiro首次将图像修复的偏微分方程(partial differential equation,PDE)方法用于图像着色,将待着色区域作为颜色修补区域,通过亮度信息Y的梯度所决定的引导场将色度信息Cb和Cr扩散至整幅图像。Yatziv等人利用加权距离色度混合技术,通过最短路径来进行图像的快速着色。滕升华等人在灰度图像上人工添加颜色线条后求解拉普拉斯方程,使得所给颜色均匀地扩散到目标灰度图像中。但这些方法都没有考虑保留图像轮廓,以致会出现颜色越界和颜色边缘模糊的问题。为克服颜色在扩散过程中的越界现象,Kang等人提出基于加权调和映射的全变差(total variation,TV)模型(以下简称Kang模型),用目标灰度图像的亮度梯度信息来刻画颜色的边缘,从而阻止颜色在扩散过程中越界。其他形式的加权TV模型也陆续被提出,用于指导颜色扩散。这些加权TV模型都是利用亮度的梯度信息来控制颜色扩散,着色效果容易受到图像轮廓中伪边缘的影响,以致着色范围较小。为了克服这一缺陷,Jin等人提出基于曲率驱动的耦合TV模型(以下简称Jin模型),该模型使用亮度的曲率信息来控制颜色扩散,减弱了伪边缘的影响,对结构信息明显的图像着色效果较好。Min等人在Jin模型的基础上,提出一种基于自然矢量TV的着色模型(以下简称Min模型),该方法能更好地保留颜色边缘,减少颜色越界。

现有的基于亮度信息驱动的颜色扩散模型在对结构图像进行着色时,能较好地保护图像的颜色轮廓。但由于这些模型中的扩散函数无法有效地刻画纹理等多细节图像的颜色边缘,在对纹理图像着色时会出现颜色扩散不均匀和越界等问题。Zhao等人结合卷积神经网络(convolutional neural network,CNN),利用深度图像先验来提取图像中的纹理等细节。在低采样率下,该方法能很好地修复图像的细节缺损信息。受文献[19]中深度图像先验思想的启发,本文在YCbCr颜色空间机制下,把深度图像先验融入到基于曲率驱动的耦合TV模型中,提出融合深度图像先验的TV着色模型。同时在即插即用(plug-and-play,PnP)框架下,结合交替方向乘子法(alternating direction method of multipliers,ADMM)给出该模型的数值求解算法,并分析该算法的收敛性。本文首先介绍相关知识点及本文模型;然后给出求解本文模型的算法;接着给出本文模型和其他模型在结构图像和纹理图像上的着色实验结果及数据,验证本文所提模型的有效性,并给出算法的收敛性分析;最后对所做工作进行总结。

1 模型介绍

1.1 预备知识

对目标灰度图像进行着色,需要选择合适的颜色空间。RGB(red,green,blue)颜色空间是目前广泛使用的颜色空间之一,除此之外还有YCbCr(luminance, two color-difference components)空间,YIQ(luminance, hue, and saturation)空间和CB(chromaticity and brightness)空间等。这些空间将彩色图像分解为色度和亮度,并与RGB颜色空间有某种联系。在本文中,⊂记为图像的支持域,⊂表示待着色区域,=表示图像中给予颜色信息的区域。 RGB颜色空间中的彩色图像可以表示为

:→={(,,):,,>0}

(1)

对于灰度图像：(,)∈→,定义拉普拉斯算子:

Δ：=∂+∂

(2)

用Δ来表示中等值线的曲率信息。

在YCbCr颜色空间中,彩色图像的亮度信息为灰度图像的灰度值,通过某种合适的算法恢复该灰度图像的色度信息(Cb,Cr),再通过YCbCr空间与RGB空间的变换关系计算出R,G,B三通道的像素值,即完成了着色的过程。

PnP框架灵活地利用了ADMM或其他临近点算法中去噪器的功能。经过变量分离技术,优化问题被分解为更简单的子问题,而正则化的临近点算子即为其中之一的子问题。正则化的临近点算子prox:→被定义为

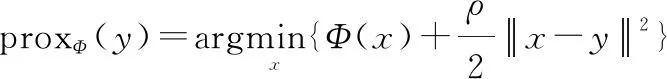
(3)

即将输入的映射到式(3)的极小值。在PnP框架下,正则化的临近点算子被去噪算法(称为去噪器)取代。本文使用去噪CNN FFDNet来替换相应的正则化临近点算子,以更好地解决相关子问题。

1.2 Jin模型

Jin等人在YCbCr颜色空间中对灰度图像进行着色,提出如下基于亮度曲率驱动的耦合TV模型:

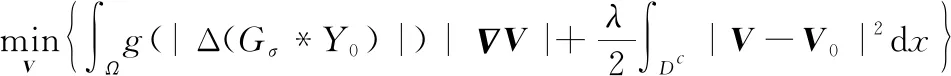
(4)

式中:*表示卷积运算；=(Cb,Cr)为YCbCr空间中色度信息；=(Cb,Cr)为已知的色度信息;()为高斯磨光核;()=11+(∈)为单调递减函数;为权重系数。

模型式(4)中的扩散函数(|Δ(*)|)利用拉普拉斯算子能有效地刻画图像的结构边缘信息并驱动颜色扩散,从而实现对目标灰度图像进行大面积着色。但是纹理等细节丰富的图像的结构、边缘不清晰,(|Δ(*)|)无法有效地刻画出这些图像的边缘,如图1(b)所示。其结果就是Jin模型在对纹理图像进行着色时,会出现颜色扩散不均匀等问题。对图1中纹理图像图1(a)进行着色,Jin模型的着色结果如图1(d)所示。很容易看出,在图1(d)中,人为添加的初始颜色与扩散后的颜色有较大的偏差。

图1 g(|Δ(Gσ*Y0)|) 的绘图及两种模型的着色效果Fig.1 Plot of g(|Δ(Gσ*Y0)|) and coloring result of two models

1.3 本文模型

为克服亮度信息驱动的局部颜色扩散模型在对纹理图像着色时出现的颜色扩散区域较小、扩散不均匀等问题,本文在Jin模型的基础上,结合CNN,提出融合深度图像先验的TV着色模型:

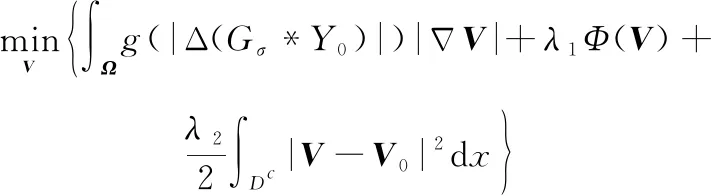
(5)

式中:=(Cb,Cr)为YCbCr空间中色度信息;=(Cb,Cr)为已知的色度信息;()、()分别为式(4)中的高斯磨光核和单调递减函数;和均是权重系数;()是隐式正则项。在PnP框架下把在自然图像数据集上训练好的二维去噪CNN FFDNet插入到模型式(5)中,以解决与()相关的子问题。

本文模型具有大数据的优势,在给定颜色较少的情况下,能有效整合耦合TV边缘捕获和CNN细节捕捉的功能,对结构图像和纹理等细节丰富的图像,均能实现较大范围的有效着色。本文对图1(a)中图像的着色结果如图1(e)图像所示,不难发现,本文模型能很好地克服Jin模型对纹理图像着色出现扩散不均匀的问题,对纹理等细节丰富的图像能实现较大范围的有效着色。

2 本文算法

本节在PnP框架下,结合ADMM算法,给出本文模型式(5)的快速数值求解算法。先引入符号

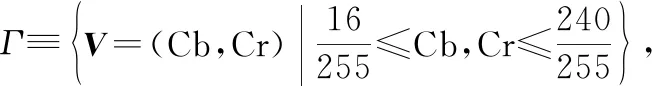
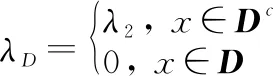
(6)

以及辅助变量、和,模型式(5)等价为如下约束优化问题:

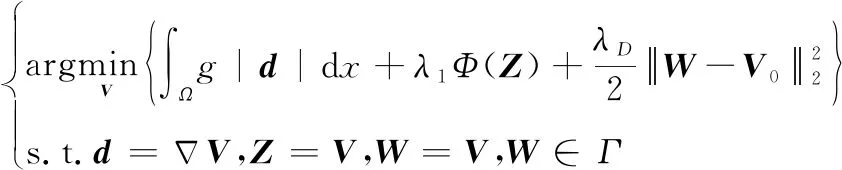
(7)

将式(7)转化为无约束极值问题,得到其增广拉格朗日函数:

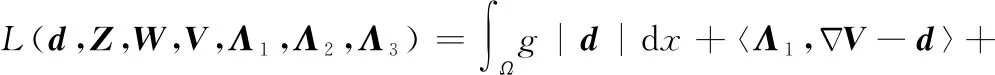
(8)

式中:,,是拉格朗日乘数;>0是惩罚参数;定义为

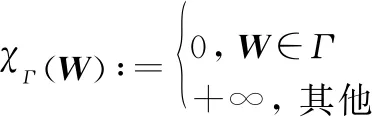
(9)

下面分别对,,,4个子问题进行求解。

(1) 求解关于的子问题:

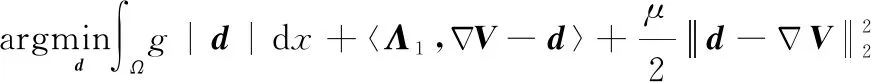
(10)

等价于

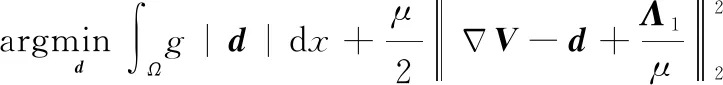
(11)

其中,对所有∈,都有()≥>0,为常数。可得

(12)

(2) 求解关于的子问题:

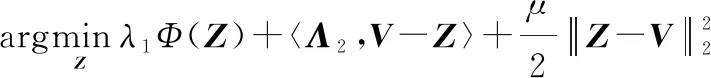
(13)

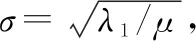
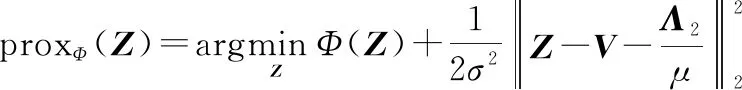
(14)

在PnP框架下,正则化的临近点算子prox:××→××被快速灵活的去噪 CNN FFDNet替换。将+馈入FFDNet中,可以解得

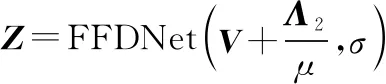
(15)

在FFDNet中,参数与噪声水平有关,此处与估计值与真实值情况之间的误差水平有关。

(3) 求解关于的子问题:

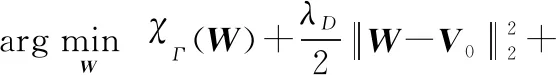
(16)

可对求导并令其等于0,解得

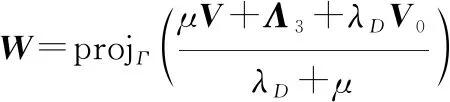
(17)

式中:

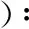
(18)

(4) 求解关于的子问题:

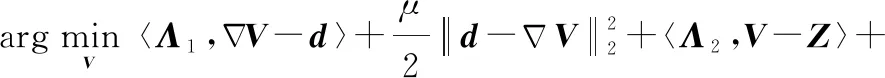
(19)

等价于求解

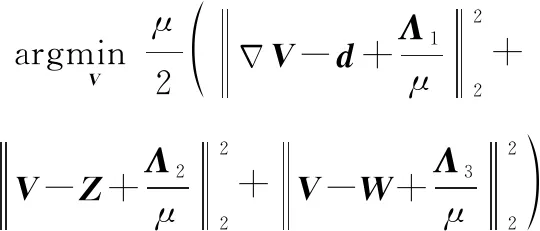
(20)

根据Euler-Lagrange方程得出

2μ-Δ=(+)---div+div

(21)

再利用快速傅里叶变换求出

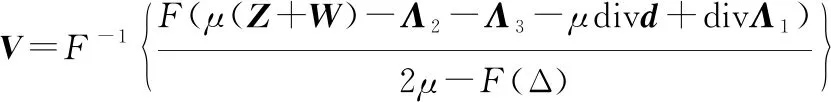
(22)

其中,及分别为傅里叶变换及其逆变换。

结合式(12)、式(15)、式(17)和式(22),本文算法的具体步骤如下。

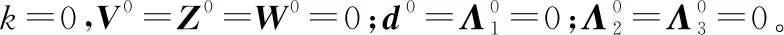
在第步迭代

由式(22)得

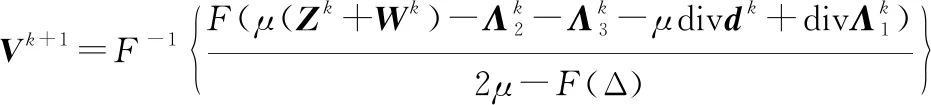
由式(12)得

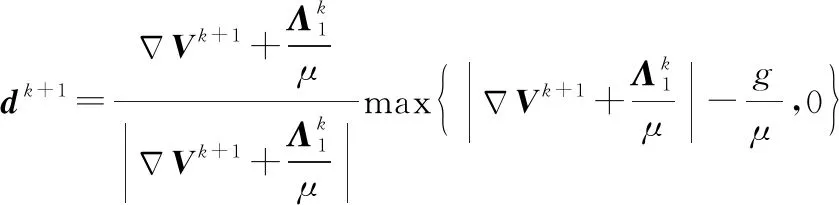
由式(15)得

由式(17)得

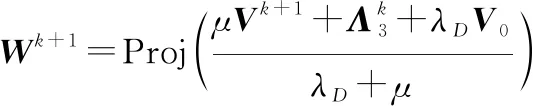
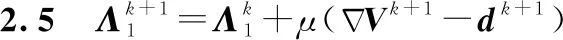
(23)

(24)

(25)

=+1

(26)

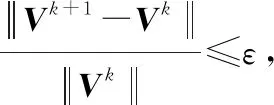
3 实验步骤及结果分析

本文图像着色的具体步骤如下。

在RGB 颜色空间上,输入一幅灰度图像,并在图上绘出适当的彩色线条。

将步骤1中输入的带有少量颜色的图像转换到YCbCr颜色空间中,并获取色度信息和亮度信息。

表1 实验中10幅图的参数设置

将彩色图像转换到RGB颜色空间中,输出图像,完成着色。

本文采用PSNR、均方误差(mean square error,MSE)和四元数结构相似性(quaternion structural similarity,QSSIM)作为着色效果的评价标准,定义如下:

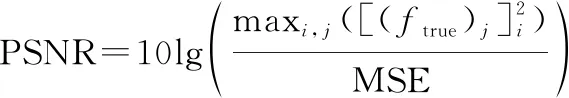
(27)

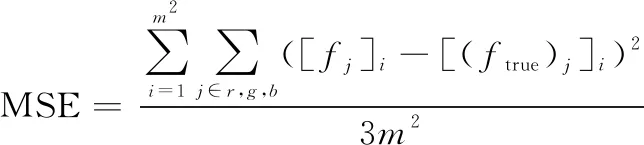
(28)

QSSIM详见Amir等人的文章,其中表示原始彩色图像,是着色后图像。的PSNR值和QSSIM值越高,MSE值越低,表示图像着色效果越佳。

为验证本文模型和算法的适用性以及有效性,本节对结构图像和纹理图像进行着色实验,并与其他模型进行比较, 其中包括两个基于深度学习的全自动着色方法: Larsson模型、Iizuka模型以及3个基于颜色扩散的着色方法:Kang模型、Jin模型和Min模型。在实验中,使用Kang模型、Jin模型和Min模型中的参数设置,并如Jin等人所提,*仅用做数学分析,采用Δ并通过有限差分法代替Δ*进行计算。由于 Larsson模型和Iizuka模型是基于深度学习的全自动着色,所以仅需输入相应的灰度图像,而在Kang模型、Jin模型、Min模型和本文模型中,输入带有部分颜色的图像。

3.1 结构图像着色

本小节展示各着色方法在结构图像(见图2)上的着色效果,实验结果如图3所示。从图3中的图像可以看出,Larsson模型和Iizuka模型所输出彩色图片与实际图像相差较大,不符合视觉效果;从图3(c)第1幅图和图3(c)第4幅图可以看出,Kang模型的颜色信息扩散范围较小;Jin模型和Min模型对结构图像着色效果较好,但在图3(d)的孩子手肘部分和左下角的番茄,图3(e)第1幅图的右上角和图3(e)第3幅图的右边苹果处颜色仍有扩散不均匀和少量越界。从图3(f)可以看出,本文模型将深度图像先验用于捕捉颜色细节部分,所以在图像细节处的着色效果较佳,生成的颜色更为准确。由此可见,本文模型对结构图像的着色效果更佳。

图2 添加部分颜色的灰度结构图像和原始结构图像Fig.2 Grayscale structural image with some color given and original color structural image

图3 使用不同模型得到的彩色结构图像Fig.3 Colorized structural image with different methods

表2列出了图3中各彩色图像的PSNR、MSE和QSSIM值,从而可以得到各模型在这4幅图上的平均PSNR、平均MSE和平均QSSIM值,如表3所示，其中最高值以蓝色标记,第二高值以粗体标记。从表3可以看出,本文模型的平均PSNR值最高,平均MSE值最低,平均QSSIM值排在第三名,但相较于第一名的 Larsson模型和第二名的Iizuka模型,其所生成的彩色图像更符合视觉效果。

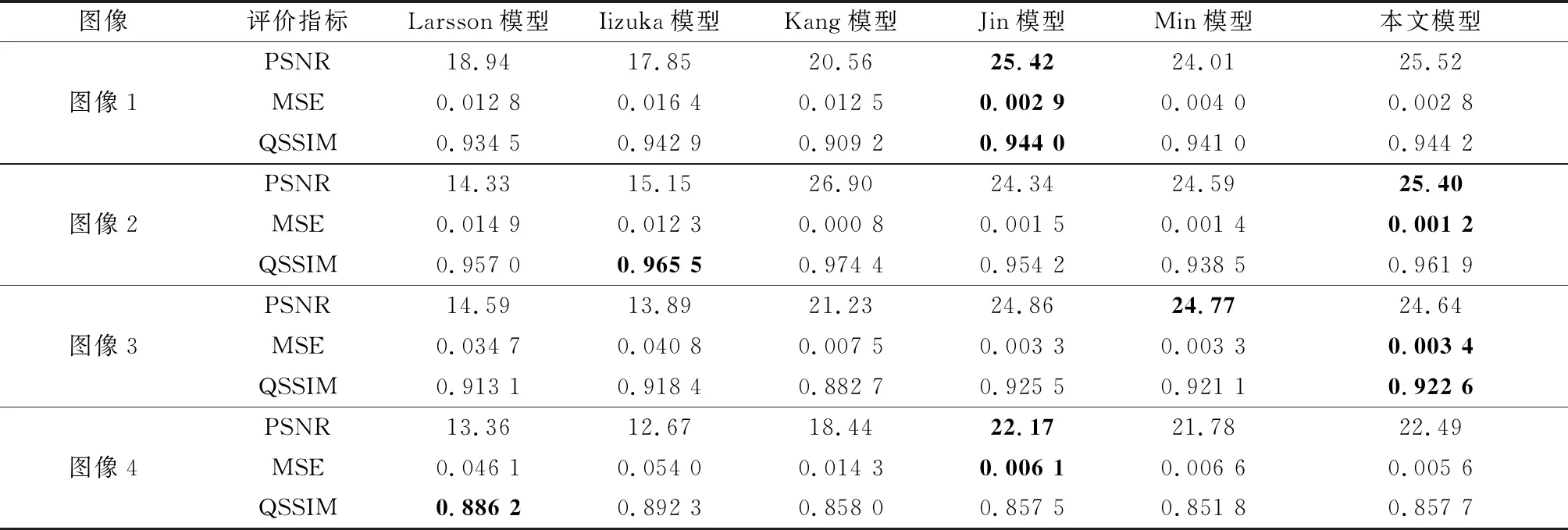
表2 图3中彩色图像的PSNR、MSE和QSSIM值

表3 图3中彩色图像的平均PSNR、平均MSE和平均QSSIM值

3.2 算法的收敛情况

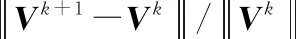
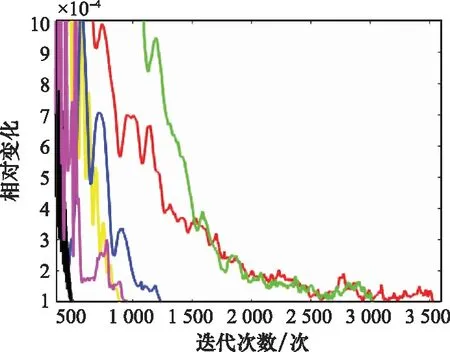
图4 本文算法在纹理图像5～10上的相对变化曲线Fig.4 Relative changing curve of the proposed algorithm in texture image 5～10

3.3 纹理图像着色

本节展示各着色方法在纹理图像(见图5)上的着色效果,实验结果如图6所示。 Larsson模型和Iizuka模型对图像5～图像10的着色效果都不佳,着色后的彩色图像与原始彩色图像相差较大,也不符合视觉效果;从图6(c)可以看出,对于纹理图像,Kang模型的颜色信息扩散范围较小;从图6(d)可以看出,Jin模型在对纹理图像着色时会出现颜色扩散不均匀,颜色越界的问题;从图6(e)中人的衣袖、草原、沙滩和鼻子边缘可以看出,Min模型对纹理图像着色依旧有明显的颜色扩散不均匀和颜色越界现象。较于这些方法,从图6(f)中的第一幅下侧、草地、沙漠、草原、沙滩、鼻子可以看出,本文模型有效整合耦合TV边缘捕获和CNN细节捕捉的功能,减少了颜色的越界,同时对图像的细节和纹理部分着色效果更佳。由此可见,本文模型对纹理图像着色效果较好。

表4列出各个模型对不同纹理图片着色后彩色图像的PSNR、MSE和QSSIM值。本文模型的PSNR值均为最高,MSE值均为最低,在图像5和图像6上取得了最高QSSIM值。表5中列出了各模型在6幅图像上的平均PSNR、平均MSE和平均QSSIM值。在平均QSSIM值上,本文模型排在第二名,与第一名的Iizuka模型相比,本文模型所生成的彩色图像更符合视觉效果。

图5 添加部分颜色的纹理灰度图像和原始纹理图像Fig.5 Grayscale texture image with some color given and original color texture image

图6 使用不同模型得到的彩色纹理图像Fig.6 Colorized texture image with different methods

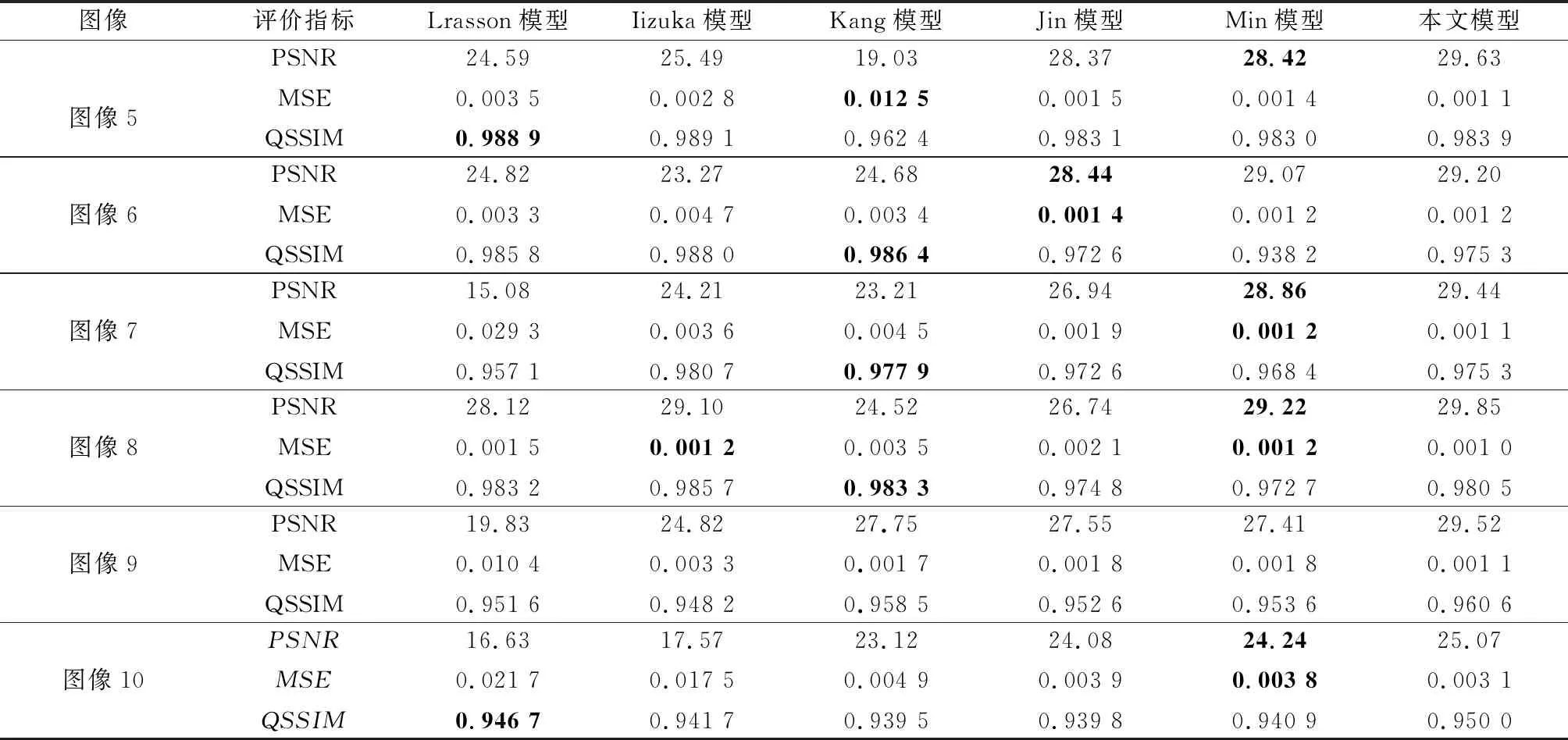
表4 图6中彩色图像的PSNR、MSE和QSSIM值

表5 图6中彩色图像的平均PSNR、平均MSE和平均QSSIM值

3.4 计算时间

在相同设备上,本文将40张图片分别在 Larsson模型、Iizuka模型、Kang模型、Jin模型、Min模型以及本文模型上进行运算,各模型的平均计算时间如表6所示。

表6 图像的平均计算时间

从表6可以看出,相较于基于深度学习的全自动图像着色方法(Larsson方法和Iizuka方法),本文算法的耗时更多,但相较于基于颜色扩散的图像着色方法(Kang方法和Min方法),本文算法的耗时更少。同时,通过对结构和纹理图像进行数值实验可知,本文算法的着色效果较上述其他方法更佳,总体优势较大。

4 结束语

本文从Jin模型出发,结合CNN 的数据补偿和细节捕捉功能,提出融合深度图像先验的TV着色模型,并在PnP框架下,结合ADMM算法进行数值求解。通过与 Larsson模型、Iizuka模型、Kang模型、Jin模型和Min模型的着色效果进行比较,可以发现,该模型能有效整合耦合TV边缘捕获和CNN细节捕捉的功能,对结构图像和纹理等细节丰富的图像,均能实现较大范围的有效着色。