带限图信号的最优采样集设计

谢 煊, 冯 辉,*, 胡 波, 李 旦,2

(1. 复旦大学信息科学与工程学院智慧网络与系统研究中心, 上海 200433;2. 上海市空间智能控制技术重点实验室, 上海 200433)

0 引 言

我们生活在万物互联的时代,分布式的网络信号广泛存在于传感器网络、社交网络等不规则的拓扑上。由于传统的时间信号无法很好地描述网络信号不同节点之间的相互关系,图信号应运而生。图信号将信号与图的拓扑结构作为一个整体表达。以社交网络为例,图的拓扑关系可以表达用户之间的好友关系,而图上每个节点的信号可以表达每个用户对某个商品的评价或对某个事件的态度等。

图信号处理通过引入图上的傅里叶变换将传统信号处理理论进行了延伸与推广。图谱理论是图傅里叶变换中最重要的理论基础,其通过图矩阵的特征值和特征向量研究图信号的图谱域特征。借助图上的傅里叶变换,研究人员已经将经典信号处理中的采样与重构及实际应用、滤波、平移等拓展至图信号处理领域。此外,图信号处理也被广泛地应用于群体检测、异常检测、半监督学习和图卷积神经网络等。

现实世界的网络中,相邻节点的信号一般具有一定的平滑性。例如,传感器网络中距离较近的传感器监测到的温湿度、气压等差异值不会很大;社交网络中有好友关系的人往往具有相似的兴趣爱好或者观点。这种图信号在节点域上的平滑特性在图谱域可以表示为带限或近似带限。在此情形下,可利用部分节点上的信号来重建或者估计所有节点的信号。根据节点信号的观测是否有噪,可将图信号的采样集设计方法分为两类:节点信号观测无噪的采样集设计和节点信号观测有噪的采样集设计。

本文主要研究观测有噪的带限图信号的最优采样集设计,其目的在于在给定采样预算的情况下选择出能使得信号估计误差最小的采样集。最优采样集设计可以通过实验设计或非实验设计的方法获得。前者主要基于对估计子性能的组合优化建模,可以纳入信号的先验知识,但通常是NP-hard的组合优化问题,需要近似求解。近似求解的方法主要分为两种:一种是贪婪算法求解;另一种是将原始问题松弛成凸优化问题进行求解。后者主要包括随机采样和基于拓扑重要性的采样。

实际中,考虑到人力物力的成本、数据传输带宽等约束,对传感器网络、交通网络等的采样与估计往往是分多阶段进行的。在已有工作中,最优采样集都是为单阶段采样设计的,即假设采样一次性完成,每个节点只允许被采样一次。由于观测噪声的存在,对某些重要节点进行多阶段观测可能会带来更好的信号估计性能。因此,无论从应用场景还是信号估计性能的角度出发,多阶段采样与估计都有更高的研究价值。

在本文的初步工作文献[17]中提出了多阶段采样的初步建模并通过松弛-量化的方法对多阶段采样集设计的问题进行了求解。本文对松弛-量化方法的性能在理论上进行了分析，证明了该方法是渐近最优的,同时也给出了松弛最优解与量化解目标函数值之差的界。此外,由于原始优化问题的目标函数中存在求逆操作,松弛-量化的方法得到的采样集在采样预算过少时有可能使得目标函数中的求逆操作无法进行,所以本文还通过扰动分析给出了保证目标函数有意义的采样预算的下界。

与具有规则拓扑的传统时域信号不同,图信号拓扑上的不规则性使得其不同节点对于信号估计的重要性会有所不同。现有的基于实验设计的采样集设计方法,往往更多关注于优化问题的求解而没有对影响节点在采样与估计中的重要性的因素进行讨论与分析。本文定性分析了不同节点采样比例的分配对采样集设计优化问题的目标函数值的影响,得到了评价带限图信号的各个节点在采样与估计中重要性的指标,并给出了其物理意义。对于大规模的图信号,求解优化问题的计算量往往是难以负担的,基于对节点在采样与估计中的重要性的分析,本文还为该场景下的采样集设计提供了复杂度较低的近似解。

最后,本文对所提出的最优采样集设计方法及近似解的性能进行了仿真验证。实验结果表明、使用本文中多阶段的采样集设计方法得到的观测可以很好地估计信号并且对噪声具有良好的鲁棒性。而近似解能够以最低的计算复杂度达到与对比算法相当的估计性能。

1 系统模型

本节将首先介绍图信号的基本概念及带限图信号的模型。然后,基于图信号估计子的形式,给出旨在最小化信号估计误差的最优采样集设计的优化问题。

=

(1)

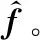
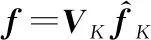
(2)

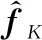
接下来首先对各个阶段采样矩阵已知情况下的图信号估计方法进行推导。假设对图信号的采样分个阶段进行,若在阶段采样个节点,则该阶段的观测信号可以表示为

=(+)

(3)

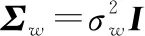
(4)

例如,对于一个有5个节点的图,阶段采样观测其第1,3,4号节点上的信号,则

(5)

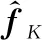
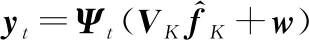
(6)

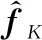
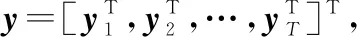
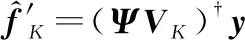
(7)

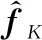
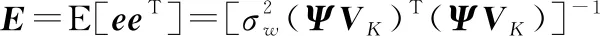
(8)

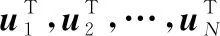
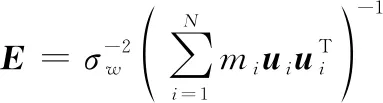
(9)

通过该变形可以发现,估计的误差协方差取决于被选择的次数,而与每个阶段分配的采样预算无关。因此,在下文中,为了减少优化问题的变量个数,我们将直接对={,,…,}进行求解。

由于误差的协方差为矩阵,不便于最小化,所以本文旨在设计最优的使得信号估计的误差协方差的某种标量化形式最小。公式的标量化主要有如下几种形式:

-optimal:()=logdet()

(10)

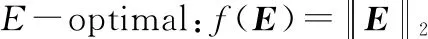
(11)

-optimal:()=tr()

(12)

因此,多阶段采样集设计的优化问题可以表达为

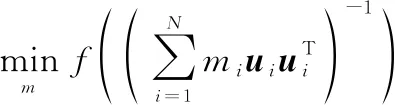
s.t.++…+=

(13)

0≤≤

∈

式中:3个约束分别对应了个阶段共采样个观测,每个节点最多采样次和采样次数为整数3个约束。

2 松弛-量化算法及分析

第1节中所述的多阶段采样集的优化问题为一个难解的组合优化问题。本节首先通过松弛-量化的方法来求得次优解。然后对所求得的次优解的性能进行理论分析。

2.1 次优解的求取

令=[,,…,],其中=为第个节点被采样的比例,对整数约束∈进行松弛,可以得到松弛的优化问题:

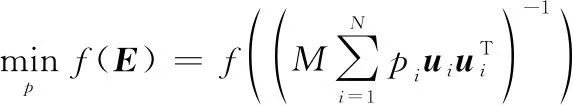
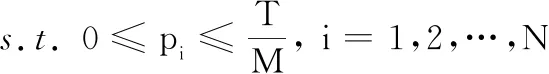
(14)

=1

上述优化问题是一个凸优化问题,可以使用标准工具包来求解。下文中,其最优解用来表示。

为了从式(14)的解中获得对应的采样集,需将的每一个元素量化成1的整数倍。与最常用的四舍五入的取整方法不同,本文使用随机量化方法来保证量化的均值是无偏的。随机量化Q∶→Q()的定义如下:∈[0,1]被等分成-1个间隔,即量化点为{1,2,…,1}。对于∈{0,1,…,-1},∈[,(+1))的量化值()是一个随机变量,定义为

(15)

对每个∈[,(+1)),都有E[()]=,所以()为的一个无偏的量化。

本文称·()为式(13)的松弛-量化解(relaxation-quantization solution,RQS)。

2.2 量化的扰动分析

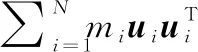
令

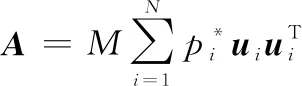
(16)

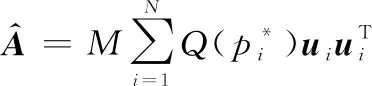
(17)

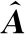
(18)

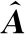
若已知是非奇异的,那么根据文献[26],与距其最近的奇异矩阵在范数意义下的相对距离满足:

(19)

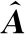
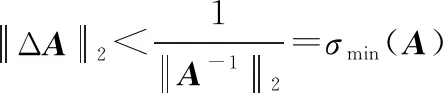
(20)

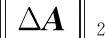
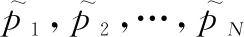
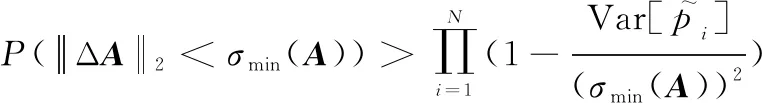
(21)

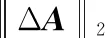
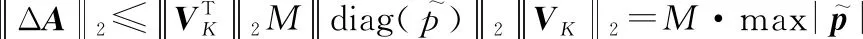
(22)

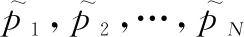
(23)

由切比雪夫不等式:

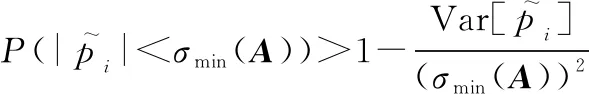
(24)

证毕

当足够大时,任意∈[,(+1)]可以近似认为是均匀分布的,即～[-12,12]。由于E[()]=,所以有

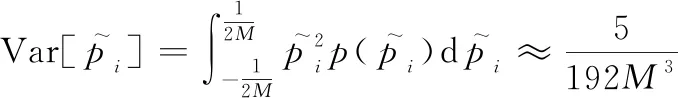
(25)

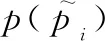
大多数情况,并不需要式(23)中的概率为1,它可以根据实际需要被设置为(0<<1)。的值决定了不同的的下界,可得如下推论。

如果采样预算满足

(26)

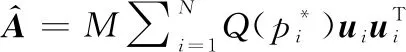
2.3 松弛-量化解的性能

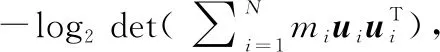
首先,可以得到如下不等式:

|()-(·())|≤
|()-(M)|+
|(M)-(·())|

(27)

当→∞,的可行域与M的可行域将变得相同,即

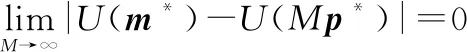
(28)

所以接下来需要证明

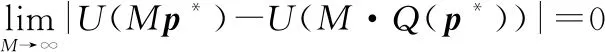
(29)

由于问题为一个凸优化问题,为其最优解,因此对的任何量化都会带来目标函数值的增加。因此

|(M)-(·())|=
(·())-(M)|=
-logdet(+Δ)+logdet()

(30)

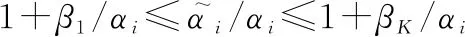
(31)

则(·())与(M)之间的差满足如下不等式:

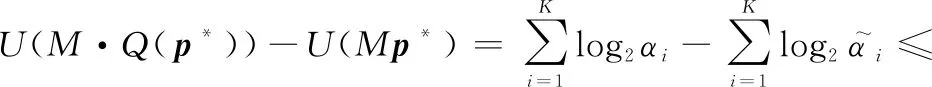
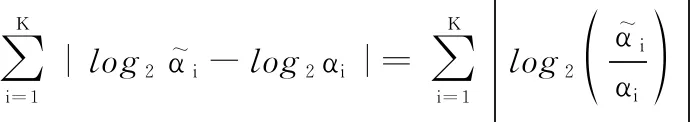
(32)

由式(31)可得

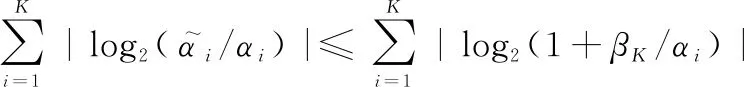
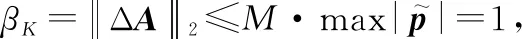
(33)

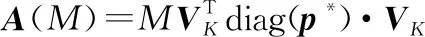
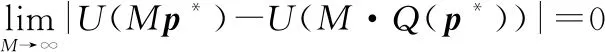
(34)

证毕

3 节点采样重要性与近似求解

本节旨在探索影响图信号的节点在采样与估计中的因素,并给出评价该重要性的指标及其物理意义。最后,基于节点重要性提出了低复杂度近似求解优化问题的方法,为大规模图信号的多阶段采样集设计提供了可行的方案。

3.1 节点采样重要性

依旧以-optimal为例,本节将通过分析式(14)中的目标函数来定性分析图的拓扑如何影响节点对信号估计的重要性。

优化问题的目标函数可以表达为

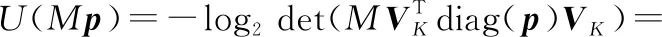
(35)

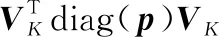
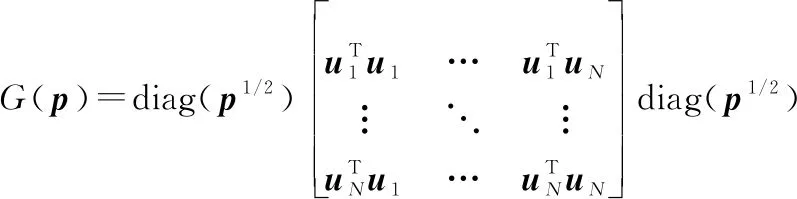
(Gershgorin圆盘定理)令为×矩阵,其第行第列的元素为。对于∈{1,2，…,},令=∑≠||为的第行的非对角元素的绝对值之和。令(,)为一个以为圆心为半径的圆,则称(,)为一个Gershgorin圆盘(Gershgorin circle,GC)。矩阵的每一个特征值都至少落在的一个GC里。

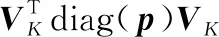
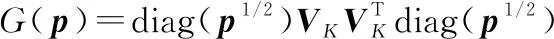
(36)

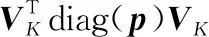
(37)

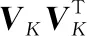
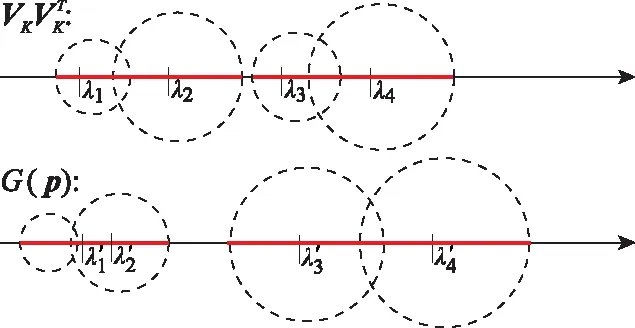
图1 GC及特征值分布示意图Fig.1 GC and locations of eigenvalues

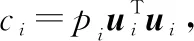
3.2 近似解

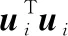
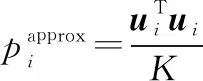
(38)

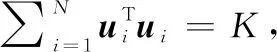
初始化:归一化系数Z=K1: 将{uT1u1,uT2u2,…,uTNuN}使用快速排序从大到小进行排列,排序后的序号集为S={s1,s2,…,sN};2: for i=1,2,…,N do3: papproxsi=uTsiusi/Z;4: if papproxsi>T/M then5: papproxsi=T/M;6: end if7: Z=Z-papproxsi;8: end for

上述求解过程中第1步的算法复杂度为(log 2),第2步到第7步的算法复杂度为()。可以发现该近似解法大大提升了算法的速度,可以应用于难以求解优化问题的大规模图信号的采样集设计中。在得到的近似解后,依旧可以通过将其量化为1的整数倍,本文将()称为近似松弛-量化解(approximate relaxation-quantization solution,ARQS)。

4 仿真结果

图2 实验中选用的图信号的拓扑Fig.2 Topologies of graph signals in the experiment

对使用不同采样集设计方法得到的节点进行信号估计,其性能使用归一化均方误差评价,计算方式如下:

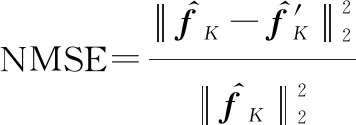
(39)

4.1 量化方法性能分析

图3 量化方法性能Fig.3 Performance of quantization method

4.2 近似解性能验证

本节将对比不同带宽下第32节中的近似解与优化问题的最优解(M)在目标函数值上的接近程度来评价其性能。实验参数设置为=128,=5,=2。实验结果如图4所示。

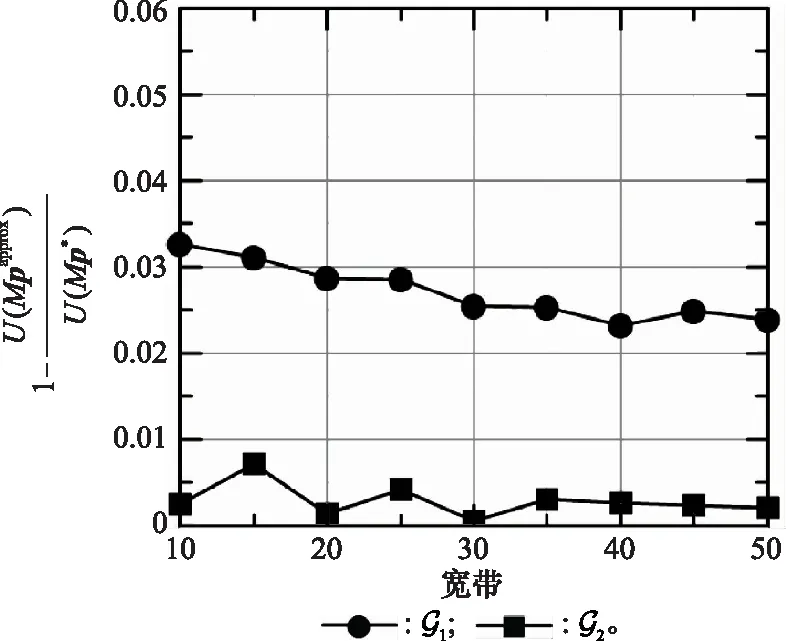
图4 近似解的性能Fig.4 Performance of approximate solution

4.3 多阶段采样性能

本节将本文的多阶段采样算法RQS和ARQS和其他文献中的单阶段采样算法的性能进行对比。对比算法如下。

M1:随机采样个不同的节点。

M2:使用贪婪算法求解优化问题得到个不同的采样节点,算法复杂度为()。

M3:求解松弛的凸优化问题,选取采样比例最大的个节点,算法复杂度为()。

M4:选择个节点使得其上的核函数能够均匀地覆盖整个图信号,算法复杂度为((||+)+)+(),其中和均为与M4中特定算子有关的参数。

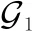
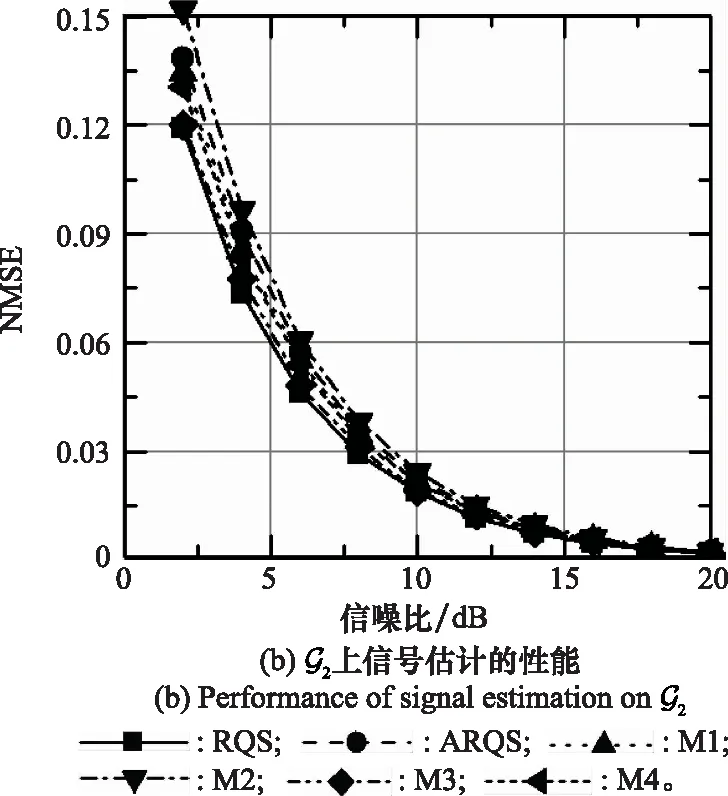
图5 不同算法在不同信噪比下的信号估计性能Fig.5 Performance of signal estimation of different algorithms under different signal to noise ratios

图6 不同拓扑下节点采样重要性分布Fig.6 Sampling importance distribution of vertices on different topologies

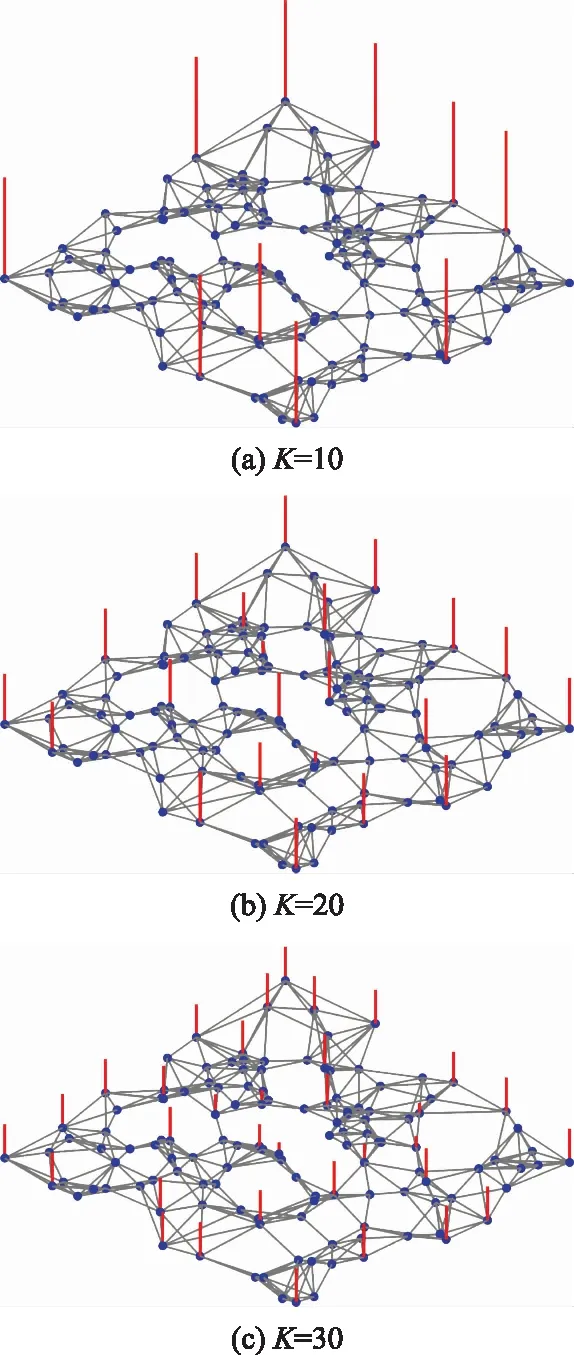
图7 不同带宽下RQS节点采样比例分配Fig.7 Sampling proportion on vertices of RQS for different bandwidths

5 结 论

本文研究了带限图信号的多阶段最优采样集的设计,提出了一种基于松弛-量化方法的最优采样集设计方法,分析了该方法有效的条件和渐近性能。通过对最优采样集设计的目标函数进行定性分析,展示了图信号的拓扑对节点采样重要性的影响,进而提出了松弛优化问题的低复杂度近似解,用于降低大规模图信号采样集设计的计算开销。仿真结果表明,使用所提算法设计的采样集在估计具有不规则拓扑的图信号时比其他现有算法有更好的性能。