初三数学复习最值问题的几点教学策略与建议

张海萍

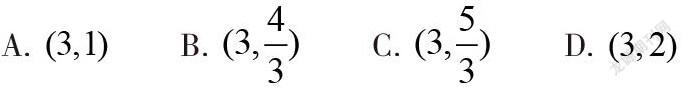
近年来，最值问题是初中数学中考的一个热点问题，这类试题往往会以填空、选择、解答压轴题的形式频繁出现。其涉及到的知识面广，运用的综合性强，集多个知识点于一体，而且问题情境层出不穷、新颖别致，全方位地考查了学生的基础知识、基本技能、解题技巧，以及数学的思维与素养能力。正因如此，对学生来说是一个难点，但是老师们在复习时若能注重教学思路＼复习策略的研究，以专题形式逐步向学生介绍这类问题的几种基本原理，同时注重培养学生转化问题的能力，帮助学生多去总结、练习这类问题解决的思想与方法，当学生形成“化折为直”的意识时，相信这类问题定能迎刃而解！

初中平面几何具有非常清晰的直观性，它的一些基本原理、图形性质学生们是熟练知晓的，也是易于掌握的，因此复习时我们可以从利用几何图形的性质解决这类问题出发，从平面几何的基本元素点与线入手，结合典型呈现模式“平面直角坐标系”，层层铺设、由浅入深地向学生介绍处理此类问题的基本思路与方法。下面本人结合教材、结合具体实例，以点的发展为思路，谈一谈初中数学复习最值问题的一些教学策略与建议。

一、点与点

几何定理：两点之间线段最短，及其延伸

七上教科书：如图，A、B是河l两侧的两个村庄。

现要在河l上修建一个抽水站C，使它到A、B两村庄的距离之和最小。请在图中画出点C的位置，并说明理由。

解题分析：两点之间线段最短，因此只有当点C在线段AB上时，它到A、B两村庄的距离之和才最小，因此点C的位置为直线l与线段AB的交点。

教学建议：本题是初中阶段最值问题的起点，学生们人人都能理解，从此入手可以增添学生研究问题的信心，教学时还可以给出具体的数据或放入平面直角坐标系中结合A、B两点坐标，再来解决问题。

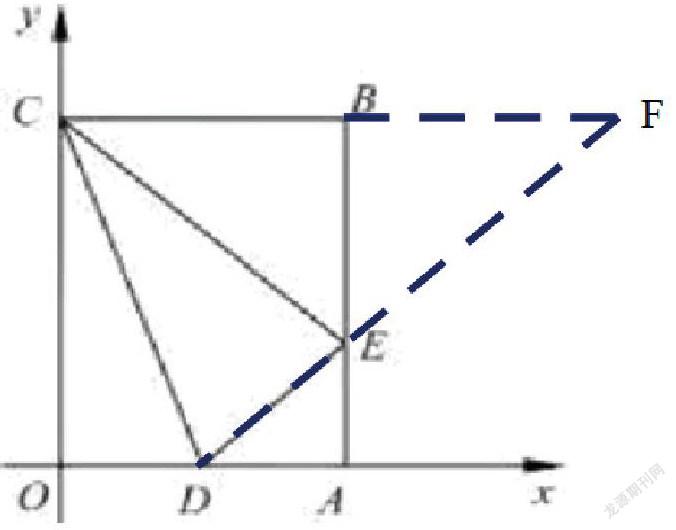
定理延伸：矩形OABC在平面直角坐标系中的位置如图所示，点B的坐标为（3，4），点D是OA的中点，点E在AB上，当△CDE的周长最小时，点E的坐标为（ ）

解题分析：△CDE的周长=CD+DE+CE，其中CD边为定长，因此△CDE的周长最小时即可转化为DE+CE为最小值时，而C、D为固定点，点E在固定直线AB上，那么这个问题类似于上述问题，唯一的区别是两固定点是位于已知直线的同侧、还异侧。同侧则直接运用定理，异侧需要运用对称点转化一下再运用定理。所以本题可以过点C作AB的对称点F（或作D点关于直线AB的对称点），连接DF交AB于点E，从而将DE+CE转化为DE+EF的值，很明显当点E在直线DF上时取得最小值。因此E点的坐标为直线DF与直线AB的交点，当然用相似的知识也可解决。

教学建议：本题首先需要利用三角形周长的定义才能将问题转化为直线AB与位于其同侧的两点C、D的问题，揭开这层面纱之后学生的心理会小有窃喜，但是能正确解得点E的坐标还是需要一定的解题经验与能力的。因此复习时老师们同时需要注重培养落实学生解析能力。

二、点与线

线是由若干个点所组成的，当这些点共线时，就形成了点与直线的问题;当这些点不共线时，就形成了点与曲线的问题。因此对于点与直线中的最值问题，教学时建议可分为两部分内容：1是点与直线;2是点与曲线，初中阶段最值问题中的曲线重点研究了圆，以下均称为点与圆。

1.点与直线的问题

几何定理：直线外一点到直线上各点的连線段中垂线段最短。

举例：如图，在平面直角坐标系xOy中，直线AB：

y=x+1与坐标轴分别交于A、B两点，点C（3，0）。

点P为直线AB上的一动点，则PC长的最小值为 。

解题分析：本题在平面直角坐标系中求点C与直线AB之间的线段长问题。

解题策略：过点C作直线AB 的垂线段CH，再利用相似三角形或锐角三角函数，亦或一次函数的一些基本知识即可迅速解决。

教学建议：本题答案很简单，学生易懂、易解决，但教学时要注重引导学生研究对象的角色转换，同时渗透多重角度解决问题的思想与方法，培养学生灵活、有效解决问题的能力，为后期综合题打下良好的思维习惯。

2.点与曲线（圆）的问题

由于一个圆将一个平面分为圆内、圆上、圆外三个部分，而圆上就是若干点所组成的曲线，因此此类最值问题的探究可分为两类：（1）圆外一点与圆;（2）圆内一点与圆。

（1）圆外一点与圆

几何定理：圆外一点与圆上各点的连线中，经过圆心的连线分别为最长与最短的。

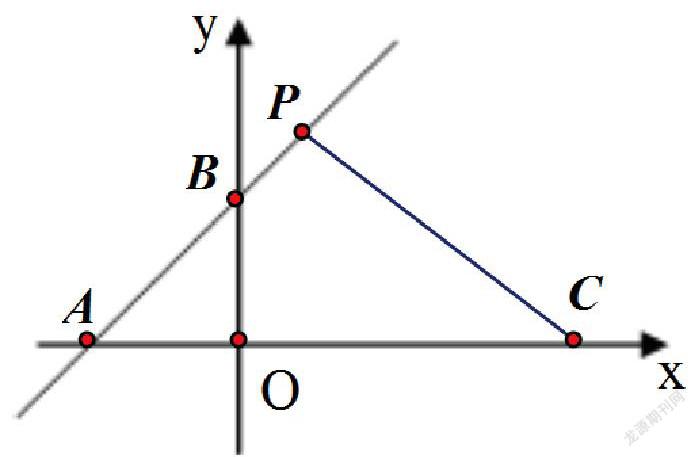
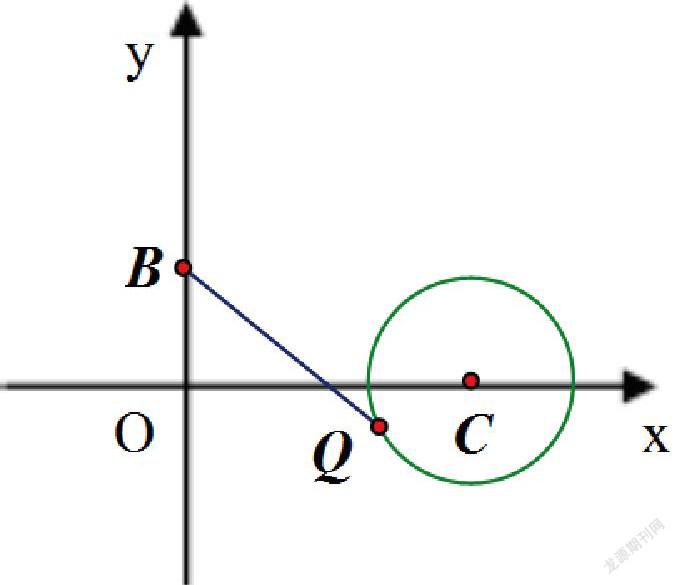
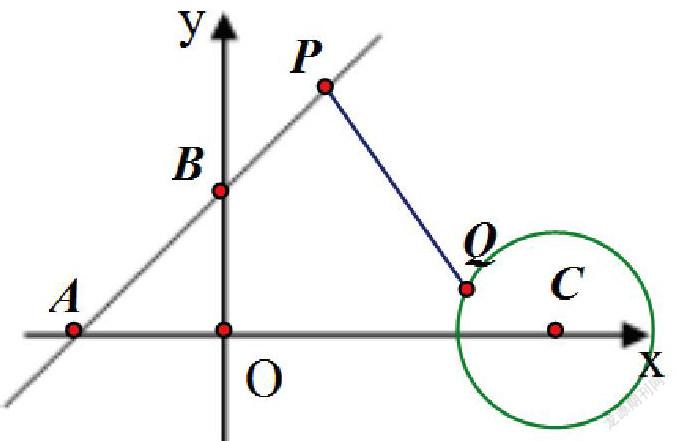
变式1：在上述问题中，以点C（3，0）圆心、1为半径作⊙C，点Q为⊙C上的一动点。求BQ的最小值为 。

解题分析：本题是在上述问题中再作⊙C，针对直线上的点B引入直线外一点与圆的问题，学生只要能够思维转换意识到直线上的点B同时也是⊙C外一点B，问题就变得迎刃而解了。

解题策略：连接BC，交⊙C于点Q，则此时BQ的长就是点B与⊙C上各点的连线中最短的连线段，再将BQ的长度转化为BC-CQ（其中CQ为⊙C的半径1）来求即可。

教学建议：举例中的问题对于学生来讲解答上是不存在任何障碍的，而变式1中的问题涉及到研究对象角色思维转换的障碍，因此教学时要注重结合具体实例培养学生从多重角度理解问题的转换能力，为问题的进一步拓展、延伸打好伏笔。

变式2：在上述问题中，PQ的最小值为 。

解题分析：本题是上述例题与变式1问题的综合，首先从圆外一点P与圆上一点Q的最值问题中发现PQ的最小值是在PC的连线与⊙C相交时的点Q处产生，即PQ=PC-CQ（其中CQ为⊙C的半径1），从而将PQ的最小值问题转化为求PC的最小值问题;

再次转化成直线外一点C与直线AB上各点的连线段中垂线段最短，便可将问题转化为例题中的基本问题来解决。

教学建议：本题的难度小有增强，体现在思维转换能力上，需要学生具有灵活的转换思想与基本的转化能力，初次接触时学生会思维反映缓慢，因此教学时需适当设置类似问题强化训练，学生们便能迅速具备这方面的能力，为后期灵活的转化能力的培养打下良好的基础。

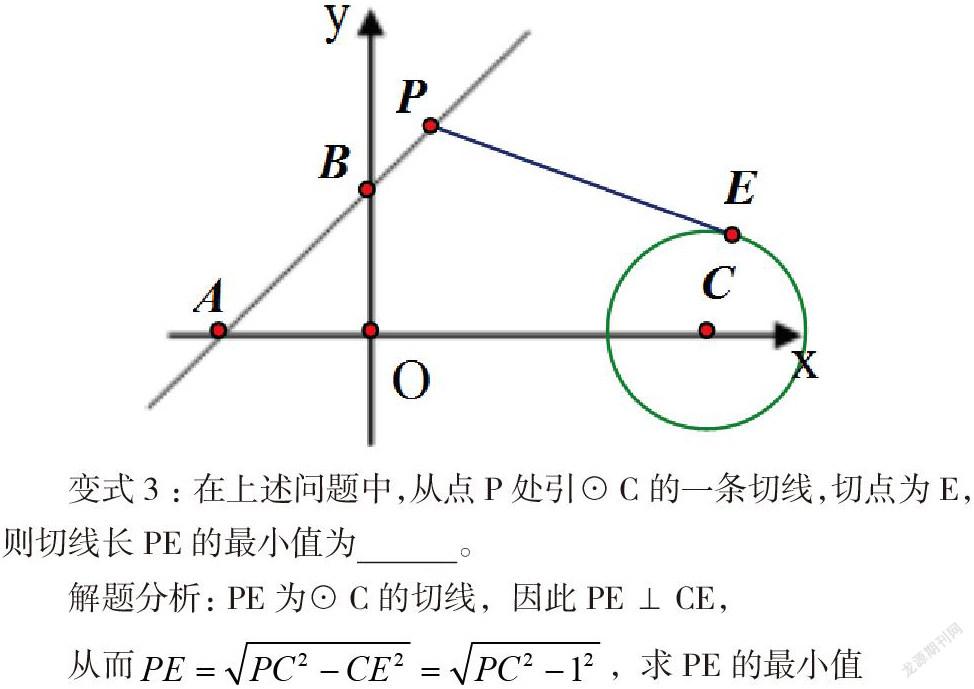
变式3：在上述问题中，从点P处引⊙C的一条切线，切点为E，则切线长PE的最小值为 。

解题分析：PE为⊙C的切线，因此PE⊥CE，

从而，求PE的最小值

转化为求PC的最小值即解决例题中的基本问题。

教学建议：本题是从另一个角度：切线的性质定理将问题转化成圆中的基本最值問题来处理，转化思想一致，只是转化的途径略有区别。教学时适当注重引导与训练，学生们处理此类问题便会得心应手，同时引导学生总结心得：转化问题的方式是因问题背景的变化而变化的，在多练习的同时更要注重多思考、多总结自己的解题心得，不能一味机械地刷题。

教学策略：圆中最值问题是最值问题中的难度提升点，大多数学生会在圆这章的几何学习中首先就产生了心理障碍，其次与代数中的重点内容函数中的平面直角坐标系相结合，这样的一个问题背景下学生们大多数会因为心理障碍而放弃了问题的研究。因此教学时我们可以从简单、易懂的问题入手，采用以上类似的变式方式，设置基础性的问题，铺设阶梯淡化问题难度，逐步将问题深化，逐步培养数学转换思想与转化能力，可以有效地帮助学生克服心理障碍，增强学生研究、解决此类问题的信心与决心。

（2）圆内一点与圆

几何定理：过圆内一点的弦中，最长的弦是直径，最短的弦是与过该点直径垂直的弦。

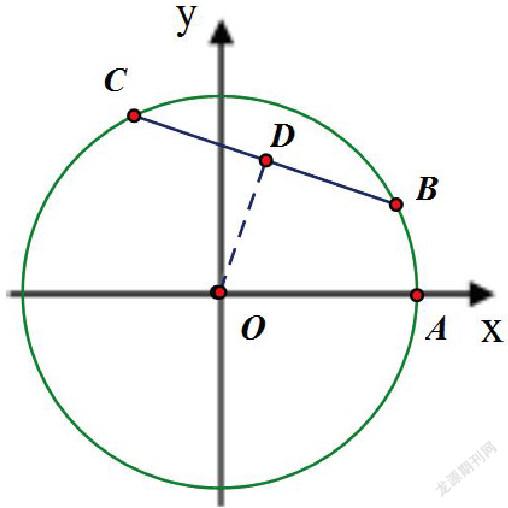
举例1：（如图，在平面直角坐标系xOy中，以原点O为圆心的⊙O过点A（13，0），直线y=kx-3k+4与⊙O交于B、C两点，则弦BC长的最小值为 。

解题分析：首先通过观察直线解析式的特征，发现该直线必定经过圆内一点D（3，4），进而发现过点D且垂直于OD的弦为所求的最短的弦，从而BC=2BD=2，其中BO为半径13、OD利用平面直角坐标系中的两点间的距离公式来求。

教学建议：本题发现弦BC所在直线必定经过点D是一个障碍，揭开这层面纱之后，问题就会变得很清晰、很简单。因此在平时教学中，要注重引导学生多去练习、总结解题心得。

教学策略：中考题中最值问题往往背景形式比较复杂多变，因此转换思想与转化能力尤其重要，只有当学生潜意识里形成这种观念时问题往往就会事半功倍了。

当然利用几何图形的性质解决最值问题只是中考考查内容中的一部分，还存在着与二次函数相结合的典型最值问题，尤其是在自变量的取值范围内的最值问题，以及难度较大的动点生成轨迹问题中的最值问题……这里本人就不逐一阐述了。

最值问题由于涉及的内容繁多、形式多样、综合性又很强，因而成为中考试题中的一朵“奇葩”！希望本人以上对此类问题的分析、研究所建议的复习策略能有所帮到大家。当然问题的形式不是一概而论的，问题的解决也不是一蹴而就的，本人上述若有不足之处敬请各位同仁批评指正。