延安新区非饱和重塑Q2黄土力学特性研究

张渭军，商 丽

(1.甘肃第三建设集团有限公司，甘肃 兰州 730050；2.黄淮学院 建筑工程学院，河南 驻马店 463000)

0 引言

填料的力学性质是填方工程研究的重点[1]，延安新区是中国规模最大的削山建城项目，仅一期工程建设面积就达10.5 km2，其中仅填方区就近1.63亿m3的土方量，填方区的最大深度达112 m，涉及多个不同功能填方区，填料首次大规模利用Q2重塑黄土。延安新区位于中国西北，该地区年降雨量较小，Q2和Q3黄土层分布位置多半高于地下水位[2-3]。因此，应开展关于非饱和重塑Q2黄土力学特性的研究。关于非饱和土力学特性的研究，Bishop[4-5]和Fredlund[6-7]先后建立了基质吸力和非饱和土有效应力的基本理论，为非饱和土的研究开辟了理论基础。Alonso[8]通过试验，得出吸力屈服方程，并引入剑桥模型中，建立了能够描述非饱和土强度-变形的巴塞罗那模型，陈正汉[9]在通过试验研究了邓肯-张模型参数随吸力的变化规律，将吸力引入到邓肯-张模型中，提出了非饱和土的线弹性本构模型。庞旭卿[10]通过研究原状黄土剪切破坏过程中的细观演化规律，构建了描述原状黄土结构破损的本构模型。在前人的理论基础上，学者们研究了非饱和Q2黄土的力学特性，如：方祥位等[11]以原状Q2黄土为研究对象，研究了吸力对其强度、变形及屈服特性的影响；于清高等[12]研究了泾河南岸水利项目原状Q2黄土不同含水率下的破坏模式及强度特性；刘新荣等[13]以王家会隧道项目中的原状Q2黄土为研究对象，根据试验规律，在经典弹塑性力学理论的基础上，建立了原状Q2黄土的非饱和弹塑性本构模型；江耀等[14]以甘肃Q2原状黄土为研究对象，通过试验分析了其应力-应变规律，并研究了其破坏应力及破坏时的孔隙水压力与围压的关系；胡再强等[15]以洛川Q2黄土为研究对象，采用环剪仪开展了单级剪切试验和多级剪切试验，研究了干密度和剪切速率对其残余强度的研究规律；宋彧等[16]通过原位试验和室内试验研究了陇东Q2黄土的湿陷性、压缩性指标、抗剪强度参数等力学指标，并论述了沿深度范围相关参数的变化规律。由于Q2黄土埋置较深，以往工程涉及的大多是原状Q2黄土。近些年，虽然重塑Q2黄土的研究受到学者的重视[17-19]，但围绕重塑Q2黄土力学特性系统研究的资料仍十分匮乏。

本研究以延安新区不同干密度重塑Q2黄土为研究对象，通过一系列不同吸力和围压的固结排水三轴剪切试验，研究了吸力对不同压实度Q2黄土力学特性的影响，可为黄土场地上填方工程的沉降变形及稳定性计算提供参考。

1 研究方法

1.1 试验设备与土样

试验设备采用应变控制式非饱和土三轴剪切仪。试验用土取自延安新区工地15 m高土坡的坡角处，所取的Q2黄土和填方区填料用土完全一致。该土的基本物理指标[20]列于表1 。

表1 Q2黄土的基本物理参数Tab.1 Basic physical parameters of Q2 loess

现场Q2黄土中有少许浆石(结核)，需剔除大块浆石，并过2 mm的筛子，由于Q2黄土中黏粒含量较Q3黄土大[21]，水分在土中扩散相对较慢，因此土样预湿均匀所需时间较长(一般需要72 h)。根据不同功能区的实测压实度79%，88%，93%，设计对应试样的初始干密度为1.54，1.72，1.81 g/cm3。

1.2 试验方案

3种不同压实度试样，均开展固结排水的非饱和土三轴剪切试验，通过脱湿来实现吸力为50，100，200 kPa，这3种不同湿度状态，控制围压分别为100，200，300 kPa，共进行了27组试验。

2 试验结果分析

文中ua，s，uw，σij，p，q[22]分别为孔隙气压力、基质吸力、孔隙水压力、总压力张量、净平均应力、偏应力。

(1)

q=σ1-σ3，

(2)

s=ua-uw。

(3)

2.1 应力-应变关系曲线

通过控制吸力和净围压来实现不同的初始应力状态，通过非饱和土三轴剪切试验所获得的不同干密度重塑Q2黄土的偏应力-轴应变数据点，并利用双曲线拟合，如图1所示。

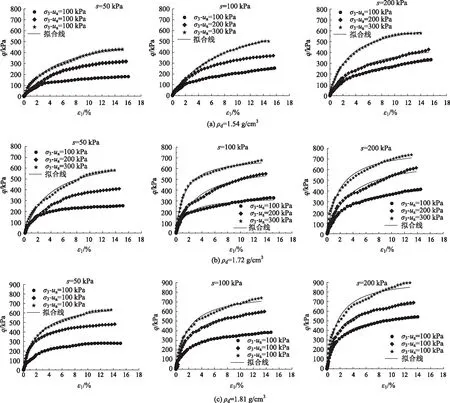
图1 不同干密度土样应力-应变关系及双曲线拟合效果Fig.1 Stress-strain relationship and hyperbola fitting of soil samples with different dry densities

从图1中可以看出，延安新区重塑Q2黄土的破坏形态仅有应变硬化和理想弹塑性两种，没有出现应变软化形式，采用双曲线拟合的效果较好，说明其曲线形态基本符合双曲线，因此，重塑Q2黄土的应力-应变关系可以采用双曲线模型进行描述。

2.2 强度参数

按《土工试验方法标准》[23]规定，选取破坏应力；各组试样破坏应力(qf,pf)列于表2。

每种干密度试样在不同吸力状态下的破坏应力点在p-q平面内的分布规律近似一条直线，如图2所示。各状态下土体的强度参数用下列表达式[24]求得：

qf=ξ+pftanω，

(4)

式中，ξ为线性拟合的截距；pf为试样破坏时的净平均应力；tanω为斜率值。

表2 不同初始干密度土样的强度参数Tab.2 Strength parameters of soil samples with different initial dry densities

内摩擦角φ′可从式(5)求得：

(5)

而土的有效黏聚力c′则由式(6)求得：

(6)

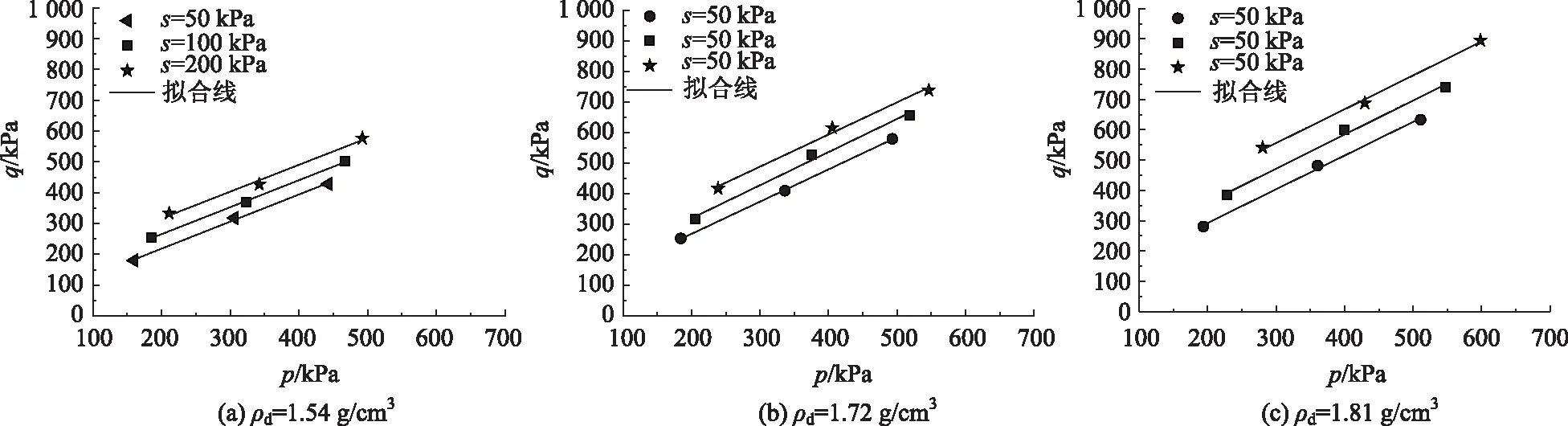
图2 不同干密度土样在p-q平面内的强度包线Fig.2 Strength envelopes in p-q plane with different dry densities

根据文献[6]中关于吸力摩擦角φb的定义，将求得的c′与s做于图3，从图3中可以看出c′-s接近线性关系，线性拟合的斜率即为φb，由此便可计算出文献[6]中抗剪强度公式中的所有强度参数c′和φ′，φb，将其值列于表2。

图3 不同吸力下黏聚力的变化Fig.3 c varying with different suctions

2.3 干密度与吸力对强度参数的影响

从表2和图2中可以看出吸力对强度参数的影响主要表现在c′上，吸力对φ′影响较小，使用时φ′可取均值。初始干密度对φ′和c′均有较大影响，分别做出φ′和c′随初始干密度的变化关系如图4～5所示。从图4中可以看出φ′与ρd呈线性关系，采用线性拟合的倾角为87.33°。

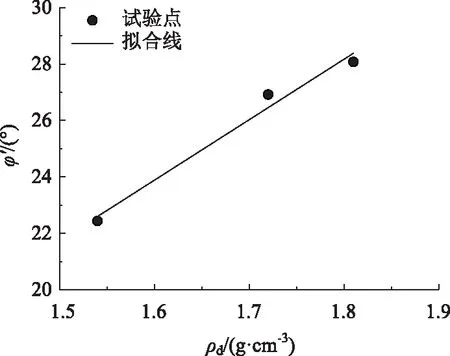
图4 不同初始干密度下内摩擦角的变化Fig.4 φ′ varying with different initial dry densities

从图5中可以看出ρd越大对应的c′越大，吸力越大，这一规律越明显。不同压实度下，吸力摩擦角均小于内摩擦角，这与文献[6]中关于其他类型土的研究结论相一致。将吸力摩擦角与内摩擦角的比值随初始干密度的变化规律做于图6，从图6中可以看出在ρd=1.54 g/cm3和ρd=1.72 g/cm3时φb/φ′相差不大其值分别为0.75和0.74，当ρd=1.81 g/cm3,φb/φ′的值为0.98，吸力摩擦角近似等于内摩擦角。

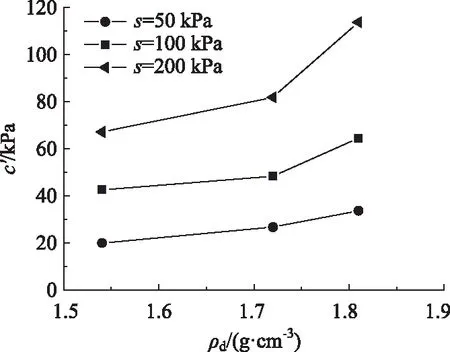
图5 不同初始干密度下黏聚力的变化Fig.5 c′ varying with different initial dry densities

图6 不同初始干密度下φb/φ′的变化Fig.6 φb/φ′ varying with different initial density

2.4 邓肯-张模型参数随干密度和吸力的变化2.4.1 切线弹性模量Et

σ1-σ3=ε1/a+bε1，

(7)

式中，a和b分别为在ε1/(σ1-σ3)-ε1坐标系中线性拟合的截距与斜率，表示的含义分别为Ei的倒数，b为(σ1-σ3)ult的倒数。按ε1/(σ1-σ3)-ε1关系对图1中应力应变点进行线性拟合，得出式(7)中的拟合参数a，b的值，列于表3中。

根据文献[24]中初始切线模量Ei与净围压关系的论述，对同一压实度试样，分别做出不同吸力下的lg(Ei/pa)和lg[(σ3-ua)/pa]的对应关系，如图7所示。从图7中，可以看出不同压实度试样，在不同吸力下lg(Ei/pa)和lg[(σ3-ua)/pa]的关系

表3 不同初始干密度土样的双曲线模型参数Tab.3 Parameters of hyperbolic model of soil samples with different dry densities

曲线均呈直线关系和文献[24]中的试验规律一致，因此文献[24]中给出的初始切线变形模量的表达式同样适用于描述非饱和土的变形。

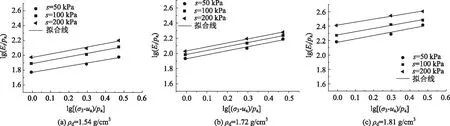
图7 lg(Ei/pa)与lg[(σ3-ua)/pa]的关系曲线Fig.7 Curves of lg(Ei/pa) vs. lg[(σ3-ua)/pa]

初始切线变形模量的表达式：

(8)

式中，pa为标准大气压；k和n分别为图7中拟合直线的截距与斜率。对图7中数据点线性拟合，得出式(8)中的参数k，n的值列于表3中。

利用表3中数据点，可以做出不同吸力下，参数k的变化规律，如图8所示，从图8中可以看出同一干密度下，参数k随吸力近似呈线性增长，其表达式为：

k=k0+m1s。

(9)

图8 k随吸力的变化Fig.8 k varying with suction

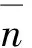
将式(9)代入式(8)即可推出非饱和土的起始切线模量的表达式：

(10)

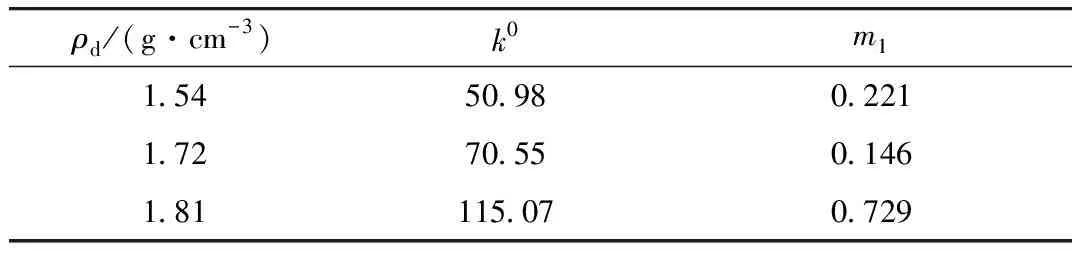
表4 各土样参数k0，m1的取值Tab.4 Values of k0 and m1 for different soil samples

采用文献[24]中切线变形模量Et的表达式：

Et=(1-RfL)2Ei，

(11)

式中，破坏比Rf=(σ1-σ3)f/(σ1-σ3)ult；应力水平L=(σ1-σ3)/(σ1-σ3)f。

土的强度准则可表达为：

(12)

式中，c′由式(6)确定，φ′由式(5)确定。则切线弹性模量Et的表达式可写为：

(13)

将式(10)代入式(13)，则非饱和土的切线弹性模量的表达式：

(14)

2.4.2 切线体积模量Kt

这里采用文献[9]中给出计算重塑Q2黄土切线体积模量的方法计算Kt，即：

(15)

式中εv为试样的体应变。

(16)

3 结论

本研究以不同压实度重塑Q2黄土作为研究对象，研究其在不同吸力作用下的力学特征，并将吸力和干密度引入到模型参数中，以描述非饱和Q2压实黄土的力学性能。得出以下结论：

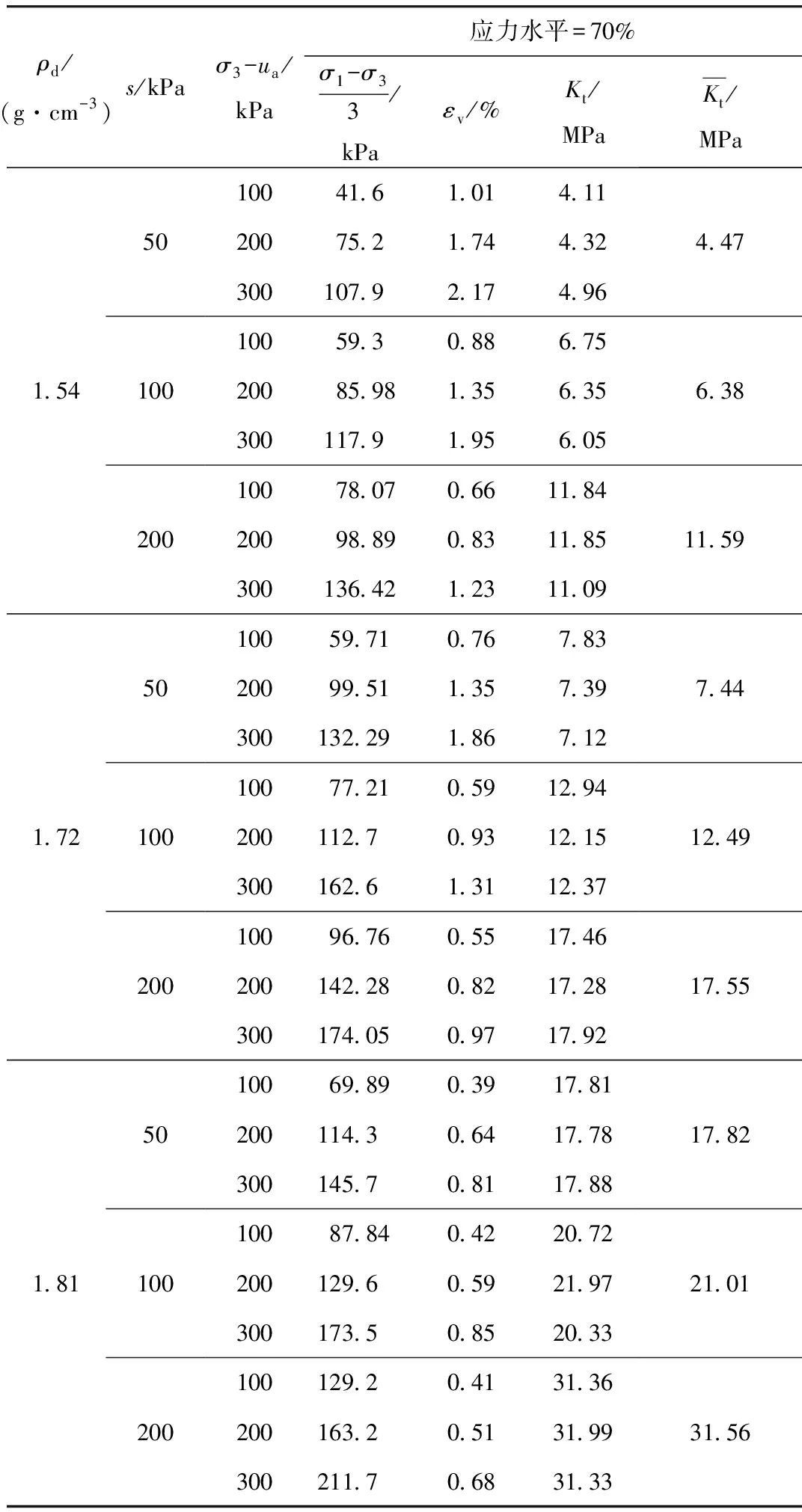
表5 土样的切线体积模量Tab.5 Tangent bulk modulus of soil samples

图9 土的切线体积模量随吸力的变化Fig.9 Kt of soil varying with suction

表6 不同初始干密度土样参数的取值Tab.6 Values of and m2 of soil samples with different initial dry densities

(1)不同干密度重塑Q2黄土在不同吸力作用下，其应力-应变曲线呈双曲线，其破坏形态仅有理想弹塑性型和应变硬化型两种。

(2)吸力对土体强度的影响主要体现在土体的有效黏聚力上，最高达80 kPa，对有效内摩擦角影响不大；有效黏聚力、有效内摩擦角和吸力摩擦角均受干密度的影响；吸力摩擦角在研究范围内总是小于有效内摩擦角。

(3)得出3种干密度重塑Q2黄土试样在不同吸力作用下的模型参数值，发现吸力值与切线弹性模量参数k值呈正比例关系，而吸力对参数n值影响不明显；切线体积模量与吸力值呈正比例关系。

(4)根据干密度和吸力对非饱和重塑Q2黄土切线弹性模量和切线体积变形模量的影响规律，将拟合结果引入到相应的公式中，得出了考虑干密度和吸力的修正计算公式。