CLLLC谐振变换器变频移相混合控制方法

邓钦瑞，何英杰，2，雷 超，刘进军

（1. 西安交通大学电气工程学院，陕西 西安 710000；2. 奥尔堡大学能源系，丹麦 奥尔堡9200）

0 引言

近年来双向DC-DC 变换器成为了研究的热点。传统的双有源桥DAB（Dual Active Bridge）DC-DC变换器利用一、二次侧开关管移相角来实现软开关，但是存在功率回流、电流应力过高等问题［1-3］。而谐振变换器可以同时在宽电压范围与宽负载范围实现一次侧开关管的零电压开通ZVS（Zero Voltage Switching）与二次侧开关管的零电流关断ZCS（Zero Current Switching），能够降低损耗，提升效率。

LLC 谐振变换器的控制方式是当前研究的热点［4］，但由于传统的LLC 谐振变换器正反向运行时的谐振状态不同导致无法同时实现软开关，并且控制策略不同导致难以控制，有学者陆续提出更多的拓扑［5-7］。其中，文献［7］提出一种双向对称的CLLC谐振变换器，在副边有额外的电感和电容，软开关可以确保在所有开关没有额外的缓冲或箝位电路，且能保证双向控制完全一致，是目前性能最优异的一种拓扑。但建模过程中忽略了谐振槽包含的励磁电感，无法保证建模的精确性。为此，在建模中考虑谐振槽包含的励磁电感，将其称为CLLLC 谐振变换器。文献［8］采用基波分析法对CLLLC 谐振变换器进行了分析，对其拓扑进行了简化和等效。基波分析法仅考虑基波分量，忽略了高次谐波对功率转换的影响，因而仅在谐振点附近比较精确，且不能反映电压、电流在具体某一工作点的时域状态。文献［9］对LLC 谐振变换器分别使用时域分析法与基波分析法进行建模，通过仿真与实验证明采用时域分析法进行谐振变换器的增益设计更为精确。文献［10］对LLC 谐振变换器进行了时域分析，其精准的解析表达式给其他拓扑的建模提供了参考。时域分析法相对基波分析法而言，可以得到更为精确的波形表达式与增益曲线以设计谐振元件参数，并且能够准确推导出实现ZVS 的边界条件，损耗计算更为精确，故可以精确地在满足限制条件的前提下进行效率优化算法的设计。但目前的研究仍缺乏针对CLLLC谐振变换器传递增益的详细、准确的时域定量分析，也就无法进行准确的损耗分析以及控制算法设计。

传统变频控制下，CLLLC 谐振变换器启动时的输出电压与冲击电流仍较大，且电压增益调节范围有限，将移相调制PSM（Phase-Shift Modulation）加入脉冲调频PFM（Pulse-Frequency Modulation）控制能够给谐振变换器带来更大的电压增益范围，特别是在电池充电变换器等场合，移相控制的应用也越来越多［11-15］。其中，文献［13］提出一种远在谐振频率前就直接从变频控制切换到移相控制的控制方法，虽扩大了电压增益范围，但没有考虑到整机效率；文献［15］提出了一种脉冲调频与单侧移相控制相结合的新型控制策略，移相控制的引入可以实现在低电压增益工况下的ZVS，但无法实现全局ZCS，且单侧移相控制只能够调节功率传输比，无法实现整个电压范围内的单位电压传输比，亦无法调节软开关范围、电流应力等特性。因此本文在此基础上提出一种变频移相混合控制方法，创新地提出了同时改变占空比与开关频率的混合过渡模态。首先移相控制实现软启动，软启动结束后进行变频控制实现稳态运行，高压输入或负载突降时采用变频移相混合控制进而过渡到移相控制，保证整个装置在宽电压范围内保持在高效率运行。

近年来碳化硅（SiC）在DC-DC 变换器领域的应用越来越多。开关频率提升到100 kHz 以上，谐振元件与变压器体积均得到缩小，提升了整机工作效率，因此本文搭建基于SiC 的CLLLC 谐振变换器进行相关研究。本文依据时域分析法进行建模，得到准确的变换器传递增益模型设计参数［16］，并研制了一台基于SiC 的CLLLC 谐振变换器以测试谐振工作特性，最后通过实验对所提控制算法进行了验证。

1 CLLLC谐振变换器拓扑结构与时域分析

1.1 CLLLC谐振变换器拓扑结构

相比传统的LLC 谐振变换器，CLLLC谐振变换器在变压器副边增设了一个LC谐振网络，因此正反向完全对称，正反向的控制方法可以完全一致。CLLLC谐振变换器电路拓扑图如图1所示，2个高频H 桥通过中间的高频变压器连接，变压器的变比为n。图中，Sx、Dx（x=1，2，…，8）分别为SiC-MOSFET 开关管及其反并联二极管；V1、V2分别为变换器输入、输出侧直流电压；Vab、Vcd分别为输入、输出侧H桥输出交流电压；L1、L2分别为输入、输出侧谐振电感，且L1=n2L2；C1、C2分别为输入、输出侧谐振电容，且C1=C2/n2；Lm为变压器励磁电感；Cin、Co分别为输入、输出侧电容。

图1 CLLLC谐振变换器电路拓扑Fig.1 Circuit topology of CLLLC resonant converter

总谐振电感Lr=L1+n2L2+Lm，总谐振电容Cr=（C1+C2/n2）/2。基于基波近似理论，负载电阻在输出侧的交流等效电阻为（8/π2）Ro，折算到输入侧为RL=（8n2/π2）Ro，其中Ro为负载电阻。双向结构完全对称，因此只需对正向分析即可，分析结果也适于反向。

1.2 CLLLC谐振变换器时域分析与参数设计

基波分析法仅考虑基波分量，忽略了高次谐波对功率转换的影响，因此结果不够精确。由于已有大量文献对基波分析法进行过阐述，本文不再赘述，而时域分析法还未应用于CLLLC 谐振变换器的详细分析。对于变频移相混合控制方法，开关管上下有一定的相移，但谐振回路以及电感电流波形仍保持对称。因此，仅分析输入侧上管驱动然后类比即可。将运行模态分为正向导通、反向导通以及谐振3种模态，下面逐一进行分析。

1.2.1 正向导通

正向导通时S1、S4导通，D5、D8导通，变压器励磁电感电压箝位于n（V2+uL2+uC2），其中uL2、uC2分别为输出侧谐振电感、电容两端的电压，电压与电流同向，其等效电路如附录A图A1所示。

进一步地，由电路基本定理以及状态模型可以得到正向导通模态下的状态变量方程为：

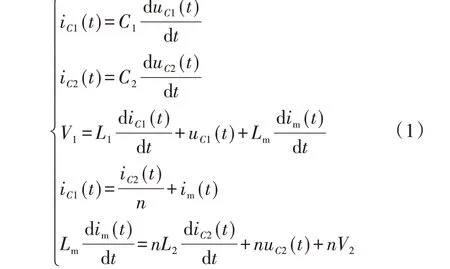
式中：iC1、iC2和im分别为流过C1、C2和Lm的电流；uC1为电容C1两端的电压。

在此过程中，谐振变换器谐振参数的边界条件可以设置为：品质因数、死区时间与励磁电感值。品质因数的限制是为了实现软启动，而死区时间与励磁电感值是为了保证实现全局软开关。

1）死区时间与励磁电感值。

定义变压器励磁电感不参与谐振时的第二谐振频率fr的计算公式为：

式中：TP为正向导通持续时间。

通过对CLLLC 谐振变换器的开关状态分析可知，在开关管关断时刻，谐振电流的最小值等于励磁电流。因此可以得到如下关系：

式中：Coss为MOSFET 的静态输出电容，具体数值见对应型号MOSFET 器件手册；Tdead为MOSFET 死区时间。

又因为存在寄生电容等因素，一般死区时间都会留有安全裕度，此处不可取等，即：

一般而言，品质因数与启动电流成反比，品质因数越小则启动电流的峰值越大。因此为了避免出现过大的启动电流瞬间烧毁器件，还必须对启动电流进行限制，即对品质因数的边界条件进行限制。根据电路可以推算出：

式中：Imax为启动电流的最大值。

1.2.2 反向导通

由于电压与电流存在相位差，当其反向时会出现反向导通模态。此时变压器励磁电感电压箝位于n（-V2+uL2+uC2），等效电路图如附录A图A2所示。

进一步地，由电路基本定理以及状态模型可以得到此模态下的状态变量方程为：

其他计算过程与正向导通模态相同。

1.2.3 谐振状态

变压器励磁电感自由振荡，电路发生谐振，等效电路图如附录A图A3所示。

进一步地，由电路基本定理以及状态模型可以得到此模态下的状态变量方程为：

2 增益分析

基于基波分析法可以非常方便地绘制增益曲线并进行相关的参数设计，但仅考虑基波而忽略了高频分量，无法反映电压与电流关系的时域状态，因此为了解决基波分析法仅在谐振频率附近能够精确描述增益的问题，基于1.2节的时域分析状态方程推导出电压、电流的时域波形，根据边界条件得到增益及电压、电流瞬时值等，准确推导软开关边界条件，进而准确地进行损耗分析以优化传输效率。

对于状态方程的求解有多种成熟的方法，本文直接引入文献［20］的Cayley-Hamilton法进行计算。

依据变压器磁链守恒，可以得到：

式中：T1为一个开关周期内，开关管从开通到谐振电流与励磁电流相等的时间；IT1为谐振电流与励磁电流相等的时刻的电感电流。

将式（14）与状态方程组一起求解，可以得到变换器电压增益M的简化表达式为：

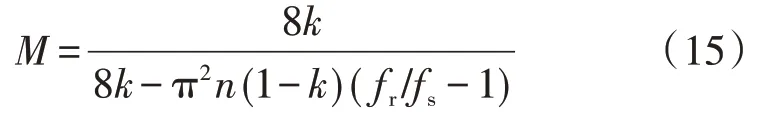
式中：fs为开关频率。

在n=1 的情况下，增益曲线如图2 所示。k值根据实际工况来确定，满足要求即可。在此基础上，可以依据增益曲线以及边界条件进行谐振腔设计。

图2 频率变化时的电压增益曲线Fig.2 Curves of voltage gain when frequency varies

3 变频移相混合控制策略

3.1 变频控制

变频控制又称扫频控制，通过改变开关频率的方式改变负载输出阻抗来调整输出电压，频率增大则输出电压减小，频率减小则输出电压增大，由于变频控制技术已经非常成熟，本文不再赘述，附录A图A4 为典型变频控制模式下CLLLC 谐振变换器的主要工作波形。

由于CLLLC 谐振变换器拓扑存在2对谐振电容和电感，相比于传统的LLC 谐振变换器拓扑动态响应较慢，因此本文采用输出电压反馈与输入电压前馈相结合的等效双闭环控制方法，控制框图如图3所示。图中，Gv2（s）为输出电压闭环控制器；Gv1（s）为输入电压对开关信号的传递函数；Gvg（s）为输出电压对输入电压的传递函数；V1ref与V2ref分别为输入与输出电压的参考值。

图3 闭环控制框图Fig.3 Block diagram of closed-loop control

通过将输入电压也引入控制闭环形成等效双闭环控制结构，可以使输入偏差通过频率及时反映出来，输出偏差也就可以得到更好更快的清除，使得动态响应速度增快，这也简化了CLLLC 谐振变换器拓扑的控制复杂程度，与传统LLC 谐振变换器拓扑相比具有更加优良的性能。

3.2 移相软启动控制

CLLLC 谐振变换器采用双重移相DPS（Dual Phase Shifting）控制时，工作波形如附录A 图A5 所示。图中，D1为输入侧H 桥的内移相比，即对应于S1超前于S4开通，且0 ≤D1≤1；D2为输入侧H 桥相对于输出侧H 桥的外移相比，即对应于S1超前于S5开通，且0 ≤D2≤1。由于传统变频启动时增益调节范围有限，最高频率处启动仍会产生较大的冲击电流，因此本文引入移相控制以调节电压增益与软开关：启动时，电压增益、占空比对（D1、D2）、输出电压均为0，输出电压从0 开始上升就可以消除启动冲击电流；此时，算法在有限制不至于上升过快的前提下，逐步改变占空比对的值，电压增益逐渐上升，输出电压随之上升直到给定输出电压值，然后软启动结束，改为变频控制方式。

3.3 变频移相混合控制

对于谐振变换器而言，电压增益宽范围与整机效率是互相矛盾的2 个指标。目前的研究均是找一个最佳切换频率点，切换频率点前后分别进行变频控制与移相控制。本文提出了一种新的控制模态，在升频的同时进行移相控制，由于频率已经达到较高的水平，在一定的频率基础上，移相控制增大的环流损耗相比升频带来的开关损耗更低，因此为了综合满足整机效率与电压增益的要求，电压增益一部分由升频满足，另一部分由移相满足，这样在满足宽范围输入电压范围的前提下提升了整机效率。

图4 为变频移相混合控制框图。图中，Kf、Kd分别为变频控制、移相控制的比例系数。输出电压反馈之后经过计算可以得到维持稳定输出需要的频率变化量，然后将其与不同比例系数相乘后分别输入变频控制模块与移相控制模块，产生新的开关频率fs与新的占空比D，这样相比传统变频控制就增大了增益范围，又因为升频的一部分改由移相替代而提升了整机运行效率。

图4 变频移相混合控制框图Fig.4 Block diagram of PFM+PSM hybrid control

在此过程中，由于变频控制与移相控制均同时进行，需要同时满足2 种控制方式的软开关范围。对于变频控制而言，软开关范围由谐振参数的设计确定，具体内容见附录B；对于移相控制而言，软开关范围由各移相比确定，具体分析如下。

移相控制情况下共有4种模态：0≤D1≤D2≤1且D1+D2≤1；0≤D2≤D1≤1且D1+D2≤1；0≤D1≤D2≤1且D1+D2>1；0≤D2≤D1≤1 且D1+D2>1。为简化分析，本文以0≤D1≤D2≤1 且D1+D2≤1 为例进行建模。如附录C 图C1 所示，一个开关周期内电感两端电压均为三电平，变换器可分为10 种工作模态分析。由图可知，iL(t)=-iL(t+Ths)，电感电流半周期近乎对称，所以只需分析半个周期的工作情况。由能量的传输与电路基本定理，可以得到各个子区间的电感电流值如下：

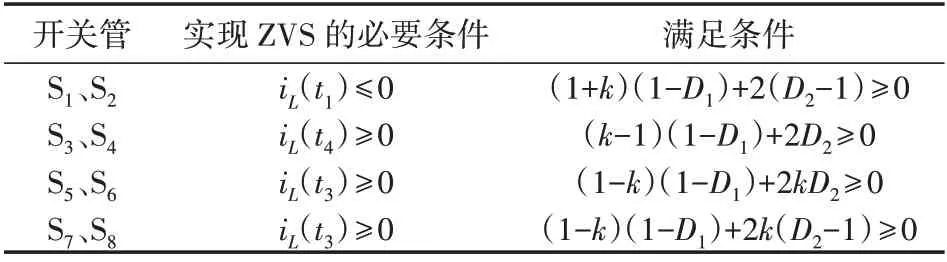
表1 开关管ZVS的约束条件Table 1 Constraints for ZVS of switches

因此，只要在移相控制过程中满足式（18），且谐振参数满足设计，就可以实现全局软开关。

变频移相混合控制流程如图5 所示。图中，f1=80 kHz；f2=240 kHz，为变频控制到混合控制的切换频率。

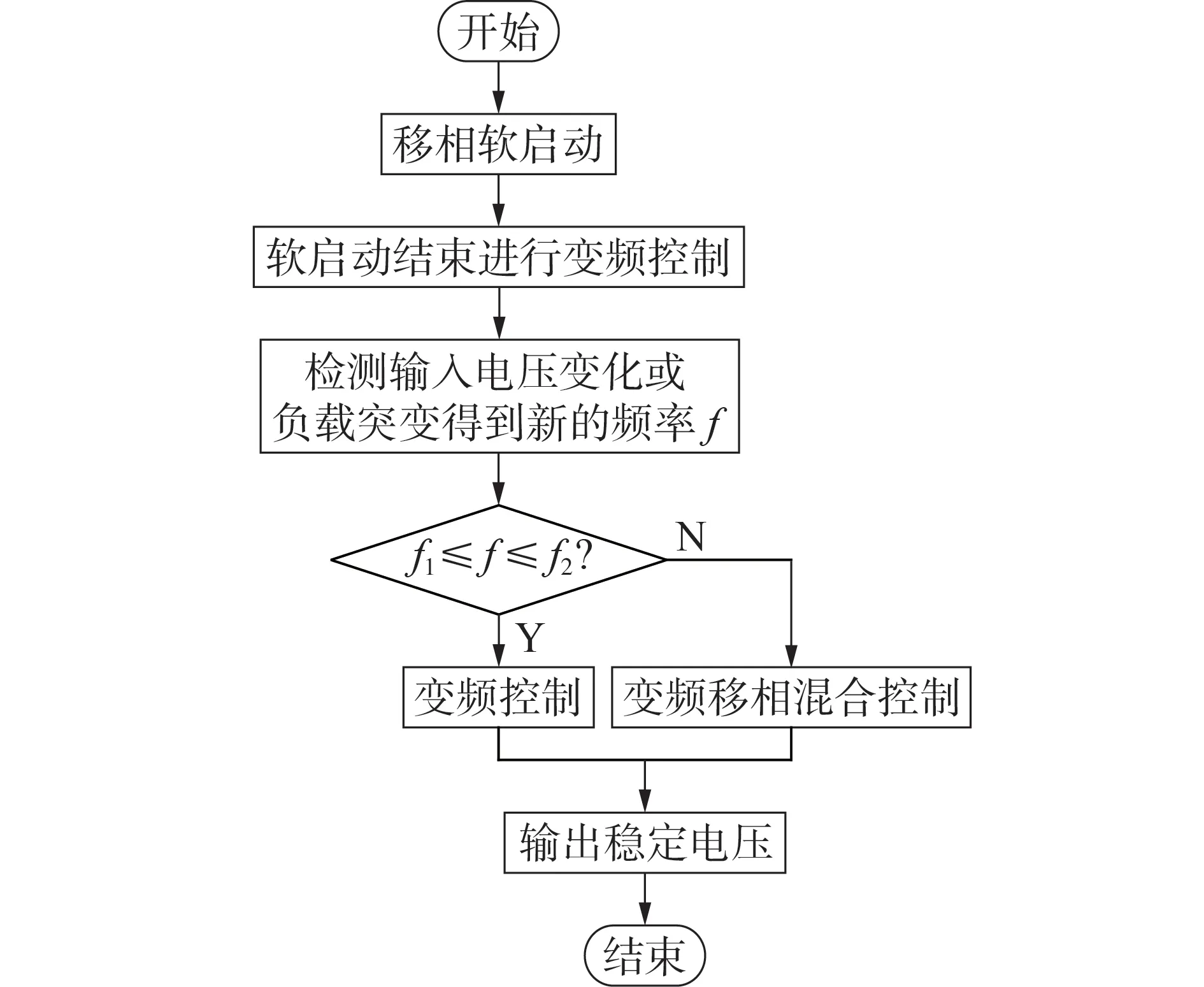
图5 变频移相混合控制流程图Fig.5 Flowchart of PFM+PSM hybrid control

4 实验验证

为验证本文所提出的基于时域分析的SiC 器件CLLLC 谐振变换器混合控制策略的正确性，基于时域分析法建模结果搭建了以TMS320F28335 为控制芯片的1 kW级CLLLC谐振变换器实验平台，其中驱动芯片采用W345-060E，开关管选用C2M0080120D。实验平台见附录C 图C2，实验平台主要参数见附录C表C1；实验结果及其分析如下。

图6 为基波分析法、时域分析法与实验得到的电压增益曲线。由图可知，实验结果与时域分析法的结果基本吻合，准确性得到大幅提升。

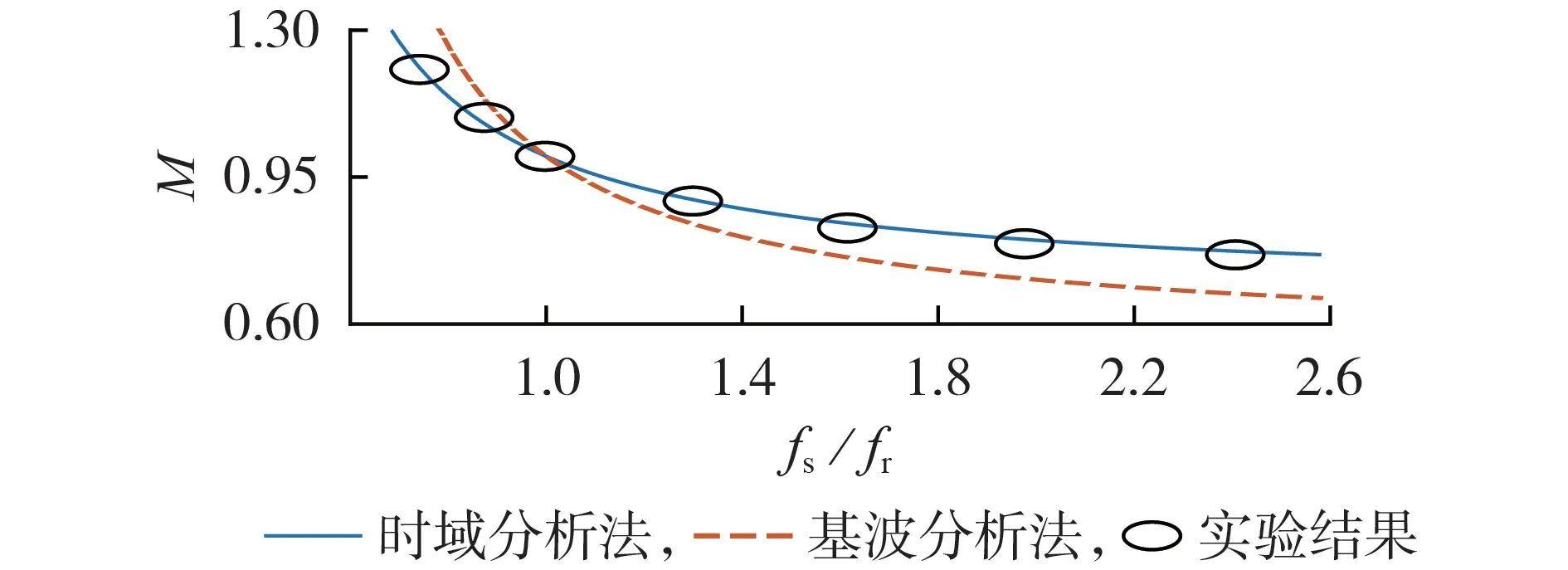
图6 2种建模方法与实验得到的电压增益对比Fig.6 Comparison of voltage gains obtained by two modeling methods and experiment

图7 为软启动波形。可以看到，使用移相控制算法的软启动效果优异，几乎没有电压、电流尖刺。

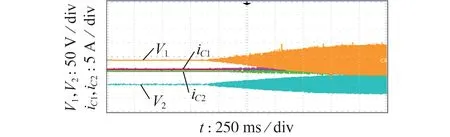
图7 软启动波形Fig.7 Waveforms of soft start

由于接近了第一谐振频率，低于第一谐振频率时变换器进入容性工作阶段，因此电压出现稍有凹陷、尖刺现象，实验波形见附录C 图C3。而当开关频率位于谐振频率附近时，电压增益为1，实验波形见附录C 图C4，此时电压超前于电流达到0，因此实现了ZVS。

图8 为相同电压增益下变频控制和混合控制的实验波形。图中，变压器励磁电流由输入侧电感电流减去输出侧电感电流得到。由图8 可知，混合控制相比变频控制在同一增益下的频率更低，证明了在相同的电压增益下混合控制可以以更接近于谐振频率的开关频率运行，整机效率更高，且在相同的频率范围内可以有更宽的电压增益范围。由图8 中输入、输出侧电流和励磁电感电流以及输入、输出电压波形可知，实验波形与理论分析基本一致，并且在全范围内都保持了ZVS以保证高效率运行。

图8 相同电压增益下不同控制方法的实验波形Fig.8 Experimental waveforms of different control methods with same voltage gain

下面绘出不同控制方法下样机效率随输出功率变化、输入电压变化的曲线。图9 为固定输出电压150 V 工作状态下的样机效率随输出功率变化的曲线。由图可知，在到达额定输出功率前，效率先升后降，但相比变频控制方法，混合控制方法在效率降低阶段由于频率上升较缓，整机运行效率要高于变频控制方法。

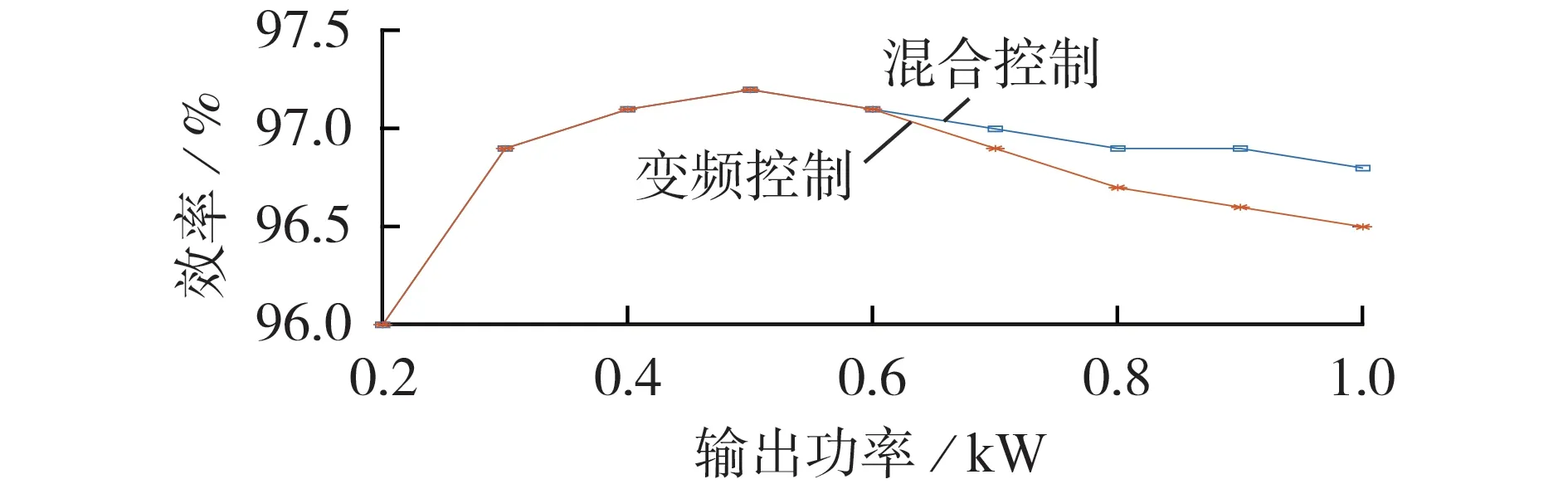
图9 效率随输出功率变化的曲线Fig.9 Curves of efficiency vs. output power

相比变频控制，由于混合控制引入了移相控制，通过改变占空比在一定程度上延缓了开关频率升高的速率，因而在同一高功率工况下混合控制下的开关频率低于变频控制，从而得到更高的效率。并且由谐振变换器基本理论可知，当开关频率高于谐振频率时，开关频率越大则效率曲线的斜率越大，因此由图9 可知，混合控制在高功率对应的高开关频率下有着优异的功率传输性能。

图10 为固定输出功率为0.6 kW 工作状态下的样机效率随输入电压变化的曲线。同样可以看出，混合控制在高输入电压对应的高电压增益、高开关频率下有着优异的电压传输性能。

图10 效率随输入电压变化的曲线Fig.10 Curves of efficiency vs. input voltage

2 种控制方法的损耗对比如表2 所示。由表可知：混合控制的开关损耗低于变频控制的开关损耗，混合控制的导通损耗高于变频控制的导通损耗；但开关损耗降低的部分高于导通损耗增加的部分，整机效率得到提升。因此，本文提出的变频移相混合控制方法的整机运行效率要高于传统变频控制方法。

表2 损耗对比分析Table 2 Comparison and analysis of loss单位：W

5 结论

本文针对CLLLC 谐振变换器，通过时域分析法进行建模，建立了各个工作模式下的状态方程，推导并绘制出电压增益曲线，在此基础上提出一种同时进行变频和移相的混合控制方法，并制造了一台基于SiC 的CLLLC 谐振变换器样机以测试谐振工作特性。

本文所引入的移相控制方法实现了软启动，降低了电流应力。所提出的变频移相混合控制方法通过引入移相控制使得变换器在宽范围内保持在开关频率附近，同时进行开关频率与移相角的控制，这样整机在满足软开关的前提下保持宽电压范围、宽负载范围内高效率运行，并且可以根据实际情况改变切换频率以获得更大的输入电压范围、负载适用范围或更高的整机效率，通过实验证明了变频移相混合控制方法的正确性和高可靠性。

附录见本刊网络版（http：//www.epae.cn）。