提高暂态稳定性的VSC-HVDC功率附加滑模控制方法

姜惠兰，李 政，肖 瑞，李希钰

（天津大学智能电网教育部重点实验室，天津 300072）

0 引言

柔性直流输电（VSC-HVDC）具有非同步联络能力强、功率调节迅速及无换相失败等优点，在新能源并网及区域电力系统互联等方面被广泛应用［1］。交流系统故障下的暂态功角失稳会对系统的安全运行造成严重影响，在交直流互联系统中，通过控制直流功率提高系统的暂态稳定性，已成为保证系统安全运行的有效手段［2］。因此研究提高系统暂态稳定性的直流功率附加控制策略具有重要意义。

分析直流功率对交流系统暂态稳定性的影响和采取附加控制策略提高系统暂态稳定性已有一些研究成果。文献［3］基于扩展等面积准则（EEAC）通过加速、减速面积定性分析直流功率对系统暂态稳定性的影响，但未定量分析二者的关系。文献［4］在多端交直流互联系统中提出了一种基于最优控制理论紧急功率调制方案。但紧急功率支援是开环控制，仅对特定系统结构和特定故障位置起作用，难以实现不同网络拓扑和故障下的稳定辅助功能。文献［5］通过对渝鄂背靠背直流工程进行时域仿真得到交流故障情况下的直流功率调制策略。但是通过实际网架结构进行仿真得出的控制策略，只对该网架结构起作用，导致控制策略适用性较差。

交直流互联系统具有强非线性特点，基于线性控制理论设计的直流功率附加控制策略［6］，会因系统运行状态的改变导致其偏离稳态运行点，使控制效果变差，因而一些非线性控制方法被用来设计直流附加控制策略。文献［7］在多区域交直流混联系统中基于协同控制理论设计了直流附加控制器，并通过仿真验证了控制器的有效性。文献［8-9］构造基于Lyapunov 能量函数的控制器，通过快速调节直流功率改善了交流系统的功角稳定性。文献［10］建立了多区域交直流混联系统的多状态Markov 模型，以此提出了基于逆最优反推控制理论的直流附加控制策略，仿真证明了该策略的有效性。文献［11］设计了基于Bang-Bang控制的直流功率附加控制器，提高了系统暂态稳定性。但以上研究多针对单机无穷大和双机系统进行理论分析和设计直流附加控制策略，缺少理论上从多机系统入手分析直流功率对系统暂态稳定性的影响，在设计控制策略时，所用交直流互联数学模型过于简单，未量化分析直流功率与多机系统暂态稳定性之间的关系。

针对以往研究的不足，本文从基于VSC-HVDC的多机交直流异步互联系统出发，综合考虑VSCHVDC 功率特性和网络拓扑结构对系统暂态稳定性的影响。依据EEAC，借助VSC-HVDC 等效导纳模型，通过推导包含VSC-HVDC 整流站功率特性和拓扑信息的系统等值机械功率变化量的表达式，建立了多机交直流异步互联系统的数学模型，寻找到整流站有功附加量与反映系统暂态稳定性的等值功角之间的量化关系。在此基础上，通过将等值功角变化速度及加速度作为状态变量建立切换面，并采用基于指数趋近律的非奇异Terminal 滑模控制，制定VSC-HVDC 整流站有功附加量的控制策略，该控制策略通过加快系统趋近稳定点来达到提高系统暂态稳定性的目的。

1 VSC-HVDC对多机系统暂态稳定的影响机理

1.1 VSC-HVDC对多机系统暂态稳定的影响途径

当交流系统发生故障时，作用在同步机转子上的机械转矩与电磁转矩会失去平衡，使同步机转子加速或减速，导致功角失稳，造成暂态稳定性问题。VSC-HVDC 通过换流站与交流电网相连，当交流系统遭受大扰动时，VSC-HVDC 可以通过改变与交流电网进行交换的功率来影响系统内同步机输出的电磁功率，进而影响系统的暂态稳定性。然而，对于多同步机系统而言，VSC-HVDC 对同步机电磁功率的影响还与网络拓扑结构有关，需要明晰VSC-HVDC对不同位置同步机电磁功率影响的不同特征，才能准确分析VSC-HVDC对系统暂态稳定性的影响。

由于VSC-HVDC对系统暂态功角的影响体现在与电网交换的功率上，可以将VSC-HVDC 功率外特性等效为动态接地导纳模型［12］，则VSC-HVDC 整流站的等效导纳模型的数学表达式见式（1）。

式中：ydc为整流站的等效导纳；gdc和bdc分别为等效电导和电纳；Pdc和Qdc分别为整流站吸收的有功和无功功率；UH为整流站并网点电压。

1.2 多机交直流异步互联系统等效转子运动方程

交直流异步互联系统结构如图1 所示。区域1 的多机系统通过VSC-HVDC 输电装置与交流电网相连。

图1 交直流异步互联系统结构示意图Fig.1 Structural schematic diagram of AC／DC asynchronous interconnection system

当图1中区域1内的交流系统发生故障时，根据EEAC［13］，可将受扰同步机划分为2 个同步机群，分别为领先群S和余下群A。将网络中所有节点分为领先群S和余下群A的同步机内电势节点、VSC-HVDC整流站并网节点H以及其余负荷节点。通过收缩处理消去负荷节点，得到只包含同步机内电势节点和整流站并网节点的系统节点电压方程为：

式中：导纳矩阵中对角线元素YSS、YAA、YHH为节点自导纳；导纳矩阵中非对角线元素为节点间互导纳；ES、EA、UH为节点电压；IS、IA、IH为节点电流。

根据式（1），将VSC-HVDC整流站等效为接地导纳后，其注入电流IH变为0，节点H的自导纳修正为：

式中：G0和B0分别为消去负荷节点后节点H的自电导和自电纳。

对修改后的节点电压方程进行再次收缩，只保留同步机内电势节点：

式中：ΔGij和ΔBij分别为节点间的修正电导和修正电纳。由式（5）可知，通过对节点电压方程的修正和收缩处理，将系统网络拓扑信息和VSC-HVDC 整流站的功率特性揉进了修正矩阵中，将VSC-HVDC 整流站对于不同拓扑位置同步机电磁功率的影响转化为对该节点自导纳和互导纳的影响。

根据式（4）、（6）和EEAC 可得反映多机交直流异步互联系统暂态稳定性的等效转子运动方程为：

式中：MSA为S群相对A群的转动惯量；δSA为转子角；Pm.SA为等值机械功率；Pc为功率偏移值；Pmax为功率极限值；γ为转子偏移角；Pm.eq为系统等效机械功率；MS、MA分别为S群和A群的等效转动惯量；n、m分别为S群和A群中同步机台数；Gij、Gik、Gjl为节点间电导；Bij为节点间电纳；Ei、Ek、Ej、El为同步机内电势；i、k、j、l为同步机节点编号；PH为VSC-HVDC 对系统等值电磁功率造成影响的部分，其表达式如式（9）所示。

式中：MT为S群和A群的等效转动惯量之和；ΔGik、ΔGjl、ΔGil、ΔGjk和ΔBil、ΔBjk分别为节点间的修正电导和修正电纳。为便于分析，本文将PH视为系统等值机械功率变化量，并将其与系统等值机械功率Pm.SA合并为Pm.eq，PH变化所导致等效机械功率的变化会改变系统的加速能量或减速能量，从而影响系统的功角稳定性。

2 整流站功率与PH的量化关系

由式（9）可知，VSC-HVDC整流站的等效电导gdc和电纳bdc隐藏在各节点导纳的修正量中，需要进一步探求整流站功率和网络拓扑对系统等值机械功率变化量PH的影响特征，以实现定量分析整流站有功和无功功率对系统暂态稳定性的影响。

考虑到同步机有较强的励磁能力，维持其暂态内电势不变［14］。同步机内电势幅值取标幺值Ei=1（i=1，2，…），并考虑到节点导纳矩阵的对称性，将式（9）改写为式（10）所示矩阵形式，式中下标(i，j)表示矩阵中第i行第j列元素。

3 VSC-HVDC功率附加滑模控制策略设计

3.1 交直流互联系统数学模型

在研究VSC-HVDC功率附加控制以提高交直流互联系统的暂态稳定性时，采用有功功率附加控制，忽略VSC-HVDC 的高阶动态特性，将VSC-HVDC的有功功率附加控制模型近似为一阶惯性环节［15］，如式（13）所示。

3.2 基于非奇异Terminal滑模控制的VSC-HVDC功率附加控制策略

由动态数学模型式（14）可得，VSC-HVDC 整流站有功功率附加量U与反映系统暂态稳定性的等值功角之间的关系是非线性的。针对二者之间的非线性关系，本文提出采用非奇异Terminal 滑模控制方法来制定VSC-HVDC功率附加控制策略。

3.2.1 非奇异Terminal滑模控制特征

滑模控制是一种非线性控制，具有参数少、设计过程简单、鲁棒性强的特点，对强非线性系统具有良好的适应性。非奇异Terminal 滑模控制是在Termi⁃nal滑模控制基础上的完善，不仅使跟踪误差能在有限时间内趋近0，还克服了奇异问题［16］。

非奇异Terminal滑模控制切换面函数：

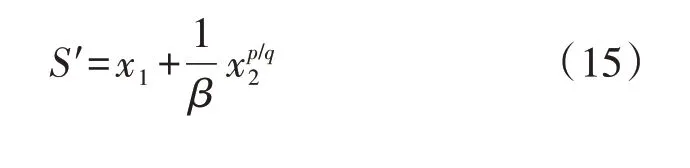
由式（16）可得，状态变量x2体现了系统等值机械功率和电磁功率的差值，通过令x1、x2趋近切换面并沿切换面到达稳定点来提高系统暂态稳定性的作用机理可以依据等面积法则来解释。系统功率特性曲线示意图如附录A图A1所示。

1）系统等值功角正摆期间。

t0时刻发生故障，因等值电磁功率小于等值机械功率而使同步机转子加速，导致x2>0、x1>0。为使x1、x2趋于切换面，此时需要调节整流站的有功功率，通过减小PH来减小x2，这会使系统等值机械功率减小，即在图A1中的加速面积由D1+D2减少到D2。在t1时刻切除故障后，功角仍在正摆时，此时系统的等值机械功率小于等值电磁功率，有x2<0、x1>0，此时仍需要减小PH，使x2进一步减小以趋近切换面，在图A1中表示为减速面积由D3增加到D3+D4。

2）系统等值功角反摆期间。

当功角反向摆动且系统的等值机械功率小于等值电磁功率时，有x2<0、x1<0，此时需要增大PH，使x2增大以趋近切换面，相当于减小反向摆动的加速面积。当功角反向摆动且系统的等值机械功率大于等值电磁功率时，有x2>0、x1<0，此时仍需要增大PH，使x2进一步增大以趋近切换面，相当于增大反向摆动的减速面积。

在减小加速面积和增大减速面积的过程中，x1和x2会快速到达稳定点，系统等值功角也会加快趋于稳定。

3.2.3 VSC-HVDC有功附加控制策略

基于VSC-HVDC有功附加控制策略提高系统暂态稳定性，其关键是合理确定VSC-HVDC 的有功功率附加量U，依据滑模控制理论，对切换面函数S′求导，如式（17）所示。

式中：sgn（·）为符号函数；ε、k为参数。指数趋近律不仅使设计的控制策略满足Lyapunov 渐近稳定要求，而且能够改善系统到达切换面的速度［16］。

最后，综合式（16）—（18）、（20）以及式（14）所示的数学模型，可得U为：

4 仿真分析

4.1 算例模型

图2 VSC-HVDC有功功率附加控制原理框图Fig.2 Block diagram of VSC-HVDC additional active power control principle

为了验证所提控制策略的有效性，本文对附录A 图A2 所示的3 机交直流异步互联系统进行了仿真分析。其中同步机SG1、SG2和SG3的额定容量分别为450、192、128 MW；VSC-HVDC整流站接入母线节点7，逆变站接入另一区域，额定传输功率为300 MW，整流站采用定功率控制，逆变站采用定电压控制。本文仿真中附加控制量的限幅为额定功率的20%［18］。设置在母线6 处发生三相短路，故障时间为［1.2，1.6］s。式（22）中的相关参数都为经验参数，根据文献［17，19］，VSC-HVDC 有功功率控制的等效时间常数取Td=0.11 s；非奇异Terminal 滑模控制中的参数取为p=5、q=3、β=1、ε=0.001、k=10。SG2和SG3属于领先群S，SG1属于余下群A。

4.2 采用附加控制策略的暂态稳定性仿真

图3 x2相对x1的变化轨迹对比Fig.3 Comparison of change trajectory of x2 vs. x1

图4 为VSC-HVDC 整流站的有功功率和有功功率附加量随时间的变化曲线。由于VSC-HVDC整流站容量的限制，有功附加量被限制在［-60，60］MW范围内。因VSC-HVDC有功功率控制模型近似为一阶惯性环节，图中整流站与电网交换的有功功率并非立即响应有功附加量U的变化。

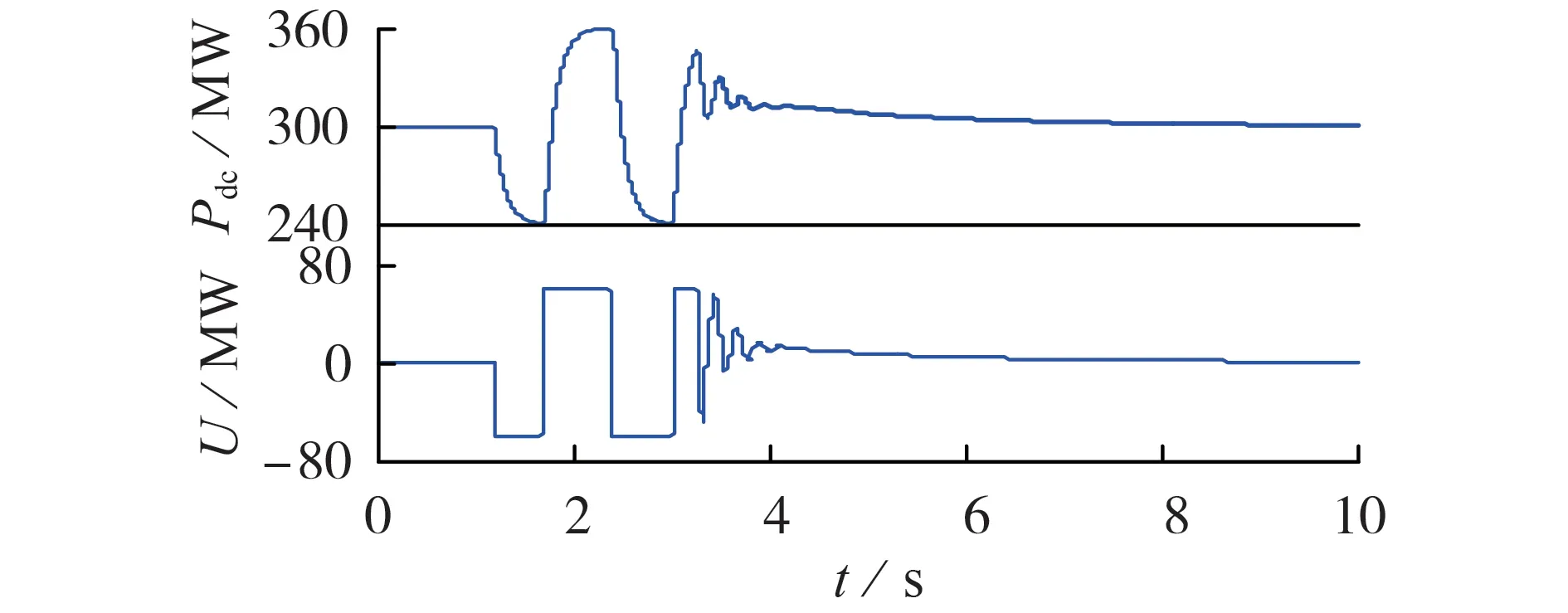
图4 VSC-HVDC整流站有功功率以及有功功率附加量波形Fig.4 Waveforms of VSC-HVDC rectifier station active power and additional active power quantity

图5 为在本文控制策略作用下系统等值机械功率变化量PH的增减情况。当功角正摆，即x1>0、x2>0和x1>0、x2<0 时，PH是减小的；当功角反摆，即x1<0、x2<0和x1<0、x2>0时，PH是增大的。可见图5中PH增减情况与3.2.2节的理论分析相吻合。

图5 本文控制策略下功角曲线及系统等值机械功率改变量Fig.5 Curves of power angle and system equivalent mechanical power change

图6 为采用本文控制策略与无控制策略的系统等值功角变化曲线对比图。可以看出，在无附加控制策略下，系统的等值功角首摆幅度大，而且至少要经过10 s的波动才能趋于稳定。而本文控制策略不仅减小了系统等值功角首摆的幅度，而且大幅减弱了等值功角波动程度，在3.5 s 左右就平息了系统等值功角的波动，有效地提高了系统恢复稳定的速度。

图6 系统等值功角曲线对比Fig.6 Comparison of system equivalent power angle curves

4.3 考虑信号获取延时的附加控制策略的适用性验证

考虑通过广域量测系统获取信息会产生延时的情况［14］，在获取控制策略所需信息时加入40 ms 和90 ms 的时间延迟，并进行仿真验证，仿真结果如图7 所示。可以看出，在时滞的情况下本文控制策略仍然能有效抑制系统等值功角的波动，能够提高系统暂态稳定性。

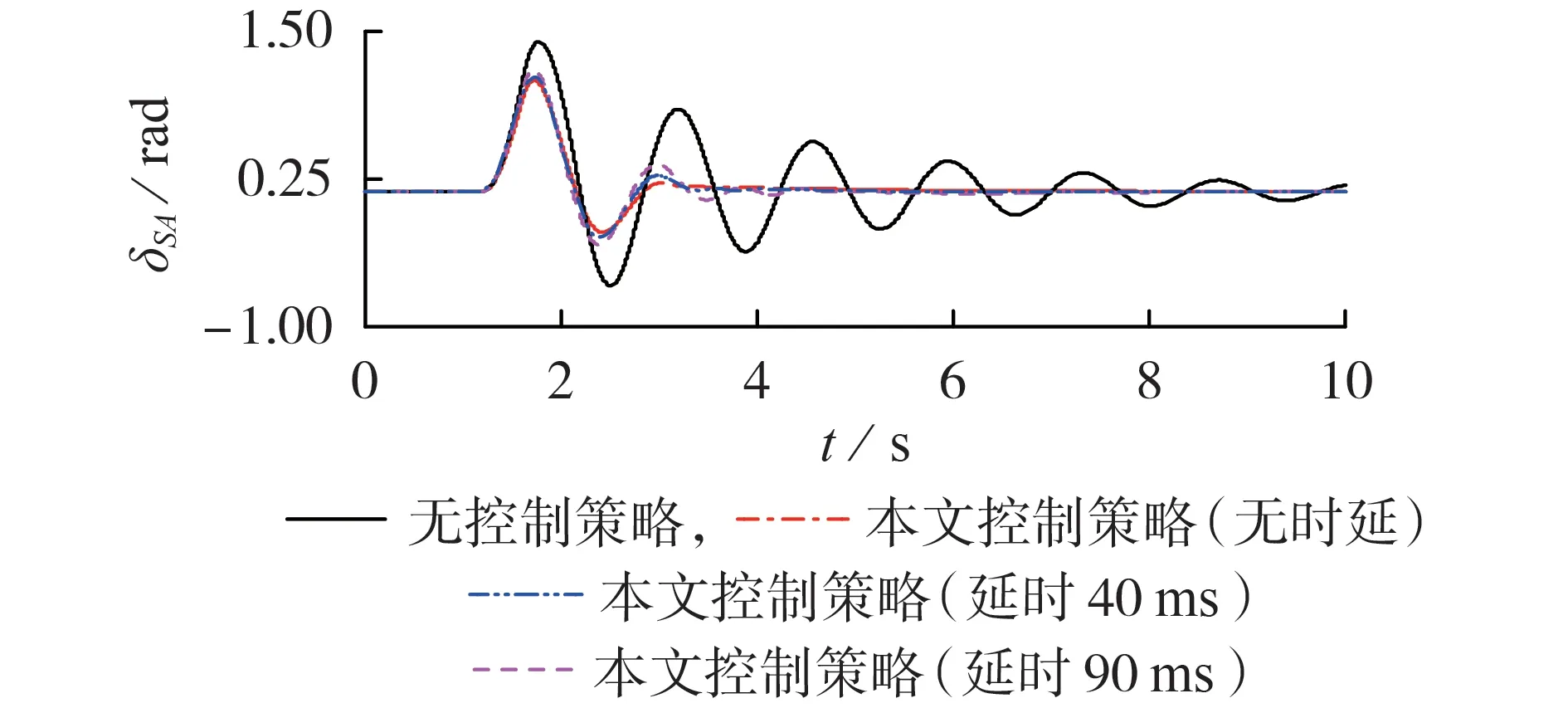
图7 延时情况下系统等值功角曲线对比Fig.7 Comparison of system equivalent power angle curves under time delay

以3 机9 节点系统算例仿真分析验证了所提VSC-HVDC 有功附加控制策略的有效性。实际上，本文基于EEAC，通过互补群惯量中心变换将任意多机电力系统等效为能反映系统暂态稳定的等值单机无穷大系统，并在此基础上制定出VSC-HVDC 功率附加滑模控制方法，因此该方法适用于复杂多机系统。

5 结论

1）通过理论推导因VSC-HVDC整流站影响产生的系统等值机械功率变化量的表达式可知，在多机交直流异步互联系统中，系统暂态稳定性不仅受到VSC-HVDC 整流站有功、无功功率的影响，还与整流站和同步机的相对网络拓扑位置及系统等值功角等因素有关。

2）建立了包含VSC-HVDC整流站功率特性与反映系统暂态稳定性的等值功角的多机交直流异步互联系统的数学模型，为设计提高系统暂态稳定性的VSC-HVDC功率附加滑模控制方法提供了理论基础。

3）设计了基于指数趋近律的非奇异Terminal 滑模控制的VSC-HVDC 整流站功率附加滑模控制方法，通过合理改变加速或减速面积来加快系统趋近稳定点，有效地提高多机交直流互联系统的暂态稳定性。

4）当VSC-HVDC 满负荷送电时，其功率附加控制可以利用过负荷能力提高系统的暂态稳定性。然而该过负荷能力受到VSC-HVDC造价和系统要求等条件的限制，当故障情况过于严重时，换流器即使以过负荷出力上限参与调制，对系统稳定的提升也是有限的，系统可能会失去稳定。

附录见本刊网络版（http：//www.epae.cn）。