基于多尺度形态学滤波的火电机组一次调频控制方法

盛 举，贾庆岩，孙建军，查晓明

（1. 武汉大学电气与自动化学院，湖北 武汉 430072；2. 国网湖北省电力有限公司电力科学研究院，湖北 武汉 430077）

0 引言

电力系统频率是衡量电能质量的重要指标之一［1］。随着新能源并网发电渗透率的不断提高，常规传统机组占比逐渐减小，电力系统的转动惯量下降，惯性支撑能力和频率调节能力不足［2-3］，各类突发功率扰动引起的电网频率异常波动频繁，对电网的一次调频控制水平和控制效果提出了新的要求。

现有的研究工作大多集中在新能源、储能侧的参数优化与控制方法改进。文献［4］分析了新能源占比提高对系统频率的影响，提出了新能源调频参数优化方案；文献［5］提出了增大等效转动惯量的虚拟同步机自适应控制策略；文献［6-7］通过改进的控制手段让新能源参与电网频率调节。上述方法固然有效，但相比同步机组，提供的惯量支撑有限，且会牺牲新能源的能量转换效率。文献［8-9］考虑了储能充放电特性，提出了储能辅助电网的调频控制策略。但储能等电力电子设备存在安装、运行、维护，材料回收成本较高的问题。从中国的电源结构来看［2］，火电装机占比超过六成，但机组调频资源的利用率较低，挖掘现有火电机组的一次调频潜力更加灵活、经济且方便。

新常态下，传统火电机组依然是电力系统中调频、调峰的主力，火电机组灵活运行和控制策略优化显得格外重要。文献［10］指出电力系统发电侧传统火电机组的调频能力还有较大的挖掘空间。文献［11］研究了火电机组的灵活运行模式，提出改进的协调优化控制策略，以提高机组应对快速负荷变化这一短时间尺度下的响应速度。文献［12］通过改进自动发电控制AGC（Automatic Generation Control）机组的控制方式以增强电力系统在二次调频这一长时间尺度下的频率调节能力。但实际系统中，AGC机组数量有限，非AGC 机组的一次调频能力尚未得到有效挖掘。上述研究均存在仅考虑单一时间尺度下的机组调频能力提升的问题。

电力系统中的功率波动主要由负荷波动和新能源出力波动引起［13］。功率波动的不同时间尺度又与火电机组调频的不同时段与频段相对应。为了提高系统在多频段的频率调节能力，文献［13］考虑了电力系统中的风电出力波动特性，对频率信号采用简单的一阶惯性滤波器进行分频滤波。该分频滤波器的实时性较好，但滤波效果较差，且只能针对单一的风电功率波动。文献［14］分析了风储火调频特性，提出了风储火联合调频策略。但基于低通滤波器的分频器的分频效果一般。文献［15］中所提出的小波分频的滤波算法的分频效果较好，但存在滤波延时较长等问题。如何兼顾分频滤波的快速性、准确性和自适应性，现有研究尚无定论。

针对以上问题，本文提出一种考虑负荷和风电出力波动特性以及基于多尺度形态学滤波的火电机组一次调频控制方法。该方法将原一次调频负反馈通道的频率信号通过多尺度形态学自适应滤波算法快速分解成高、中、低频3 个频段的信号，在不同频段信号内设置合理的调差系数，可在全频段内有效地降低负荷和风电出力波动对系统频率波动的影响，从而提高机组全频段的一次调频能力。

1 电力系统调频过程分析建模

电力系统的调频过程主要由一、二次调频组成。其中一次调频主要利用火电机组的锅炉蓄热蓄能对频率进行有差调节［16］。为了消除一次调频造成的频率偏差，二次调频主要通过改变机组原动机出力设定值，从而将系统频率恢复到标准值。

1.1 电力系统频率响应模型

研究电力系统频率的长时间尺度行为（一、二次调频）时，基本可以忽略发电机之间的相对摇摆，认为发电机之间严格地保持同步运行，系统中的任意节点和机组都会有相同频率动态变化的过程；负荷波动和风电出力波动范围通常较小，可以进一步忽略电压变化的动态过程。因此可以使用等值的单机模型来进行计算分析［17］，该系统频率响应模型含有一、二次调频通道，具体模型控制框图见附录A 图A1，参数设置见附录A表A1。

1.2 系统频率响应动态过程

当负荷发生功率扰动时，系统频率响应的动态过程如图1 所示。发生负荷扰动前，系统频率在标准频率fN附近上下波动。若频率偏差在死区范围±fdb内，则主要通过机组的惯性作用吸收这部分频率波动；若频率偏差越过死区，则一次调频开始作用，将频率偏差恢复到死区范围内。发生较大的功率扰动后，系统频率恢复到标准范围的过程主要经历以下3个阶段［18］。

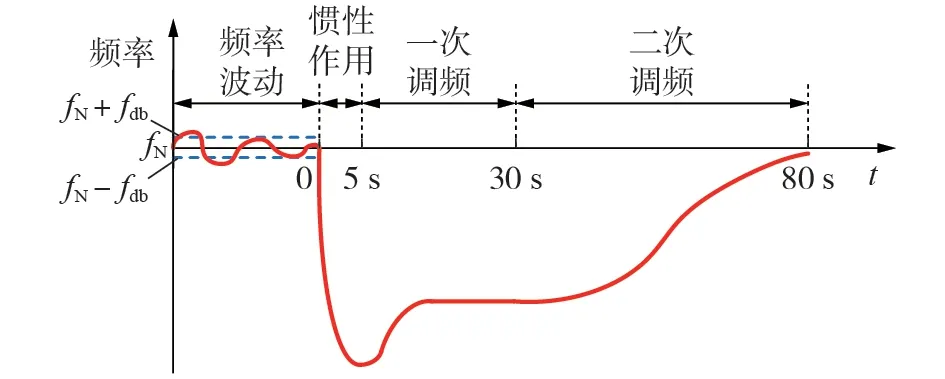
图1 系统频率响应动态过程Fig.1 Dynamic process of system frequency response

第一阶段，［0，5）s 内，因为系统存在发电缺额，系统频率开始衰减，发电机的转子释放能量，限制频率的衰减速度。这个阶段主要通过机组的惯性作用（动力蓄能特性）进行系统频率调节。

第二阶段，［5，30）s 内，在机组惯性作用发生的2～3 s后，机组的调速器逐渐响应并改变原动机输出功率，增加发电机的输出功率。这个阶段主要通过机组的一次调频作用进行系统频率调节。

第三阶段，［30，80］s 内，AGC 机组在可以控制的旋转发电备用容量范围内，恢复系统联络线功率和系统频率，主要通过运维调度人员手动调节。这个阶段主要通过机组的二次调频作用进行系统频率调节。

上述3 个阶段的调频作用示意图见附录B 图B1。常规电力系统中，一般绝大多数的机组都承担一次调频任务，少部分机组被安排进行二次调频任务。一次调频是电力系统中最频繁也是最重要的频率调节过程。如何挖掘火电机组一次调频能力，使一次调频在惯性作用和二次调频的时间尺度上也“发挥余热”，对增强系统频率的安全稳定，提高机组的灵活性具有一定意义。

1.3 电力系统调频参数的影响

调差系数R是汽轮机控制系统静态特性曲线的斜率，通常以对应空负荷与满负荷的转速差值与额定转速比值的百分数来表示［16］。

当本文系统频率响应模型的负荷端出现0.05 p.u.的阶跃扰动时，不同调差系数下系统频率的响应曲线如图2 所示。图中，调差系数越小，机组出力的调节能力越大，但是会导致闭环控制系统的不稳定，出现系统频率振荡甚至发散的情况；调差系数越大，机组出力的能力越小，一次调频的能力越弱。因此，机组调差系数的设置不宜过小也不宜过大。

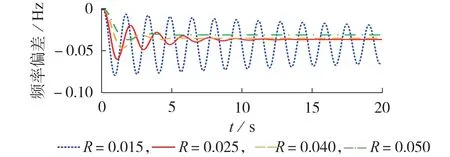
图2 不同R的系统频率响应曲线Fig.2 Frequency response curves of different values of R

一次调频控制系统的开环对数特性图见附录B图B2。作为控制系统的频域性能指标，剪切频率ωc、相位裕度γ和增益裕量K越大，则系统越稳定，但控制系统的响应速度也会变慢。工程设计一般要求ωc<0.04 Hz，γ的取值范围为［5°，30°］，K>5 dB。

当调差系数从0.050 减小到0.015 时，系统的剪切频率ωc不断右移，由0.028 Hz 增大至0.056 Hz；系统的相位裕度γ不断减小，由初始的32.43°减小至-2.65°；系统的增益裕量K不断减小，由初始的9.5 dB减小至-1.27 dB。在此变化过程中，一次调频闭环控制系统由稳定变成失稳状态，故调差系数的设置存在下限。参考国家电网公司标准Q／GDW 669—2011《火力发电机组一次调频试验导则》给出的大功率机组调差系数设置范围4%～5%，在满足系统稳定性的前提下，本文的调差系数范围设置为3%～5%。

2 多尺度一次调频控制方法

传统的一次调频控制方法通过负反馈通道将频率信号转化阀门动作指令信号［16］，进而改变原动机的出力，一般设置固定的调差系数。随着电力系统中的功率波动组成愈加复杂，常规一次调频方法对系统中各个频段的功率波动的调频控制能力逐渐下降。

2.1 系统频率响应特性分析

根据1.1节建立的电力系统频率响应模型，系统的频率响应传递函数H(s)表达式如式（1）所示。

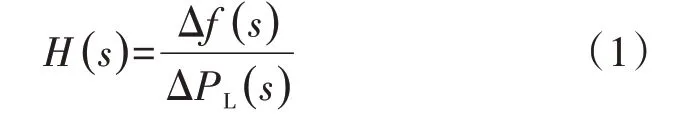
式中：Δf(s)为系统频率偏差；ΔPL(s)为系统负荷功率偏差。

系统的频率响应传递函数H(s)的物理含义为系统对功率波动的调节能力，当系统对功率波动的调节能力越强时，H(s)越小。H(s)的闭环幅频特性和相频特性见附录B 图B3。图中，对比仅靠机组惯性、仅靠一次调频作用、仅靠二次调频和机组惯性以及一、二次调频共同作用这4 种情况下的幅频特性曲线。在大于0.38 Hz的频段内，仅靠机组惯性作用的调节能力是大于一、二次调频共同作用的。对于这个频段的功率波动，调速器的死区需要合理设置，以最大化利用机组的惯性作用；在［0.03，0.38］Hz的频段内，系统一次调频的作用则显著大于二次调频和机组惯性作用；在小于0.03 Hz 的频段内，显然二次调频的作用最强。

从频域的尺度内分析，上述3 个频率尺度的调频作用示意图如图3 所示。多尺度一次调频控制方法将一次调频负反馈通道的频率信号通过多尺度滤波器分成高、中、低3 个频段，分别对应机组惯性作用、一次调频、二次调频的频段。再通过对3 个频段的信号合理地设置调差系数，即可增强系统对全频域的功率波动的频率调节能力。

图3 频率调节的频域频率尺度Fig.3 Frequency scale of frequency regulation in frequency domain

2.2 多尺度形态学滤波器的分解算法

常用的分频滤波方法有一阶惯性滤波法、卡尔曼滤波法、小波分析WA（Wavelet Analysis）、傅里叶变换FT（Fourier Transform）等。

数学形态学MM（Mathematical Morphology）是一种非线性信号处理方法。不同于WA 方法、FT 方法等频域分析方法，MM 方法提供了直接在时域进行的多时间尺度分解算法。作为一种启发式算法，通过对原信号进行填充计算，可以很好地保持原信号的信息，具有运算量小、滤波精度高、滤波延时低的优点，因此很适合作为信号的多时间尺度分解算法。

设输入信号为x(n)，n∈{0，1，…，N-1}；结构元素为γ(m)，m∈{0，1，…，M-1}。函数的膨胀与腐蚀运算分别为：

参考文献［20］中改进的自适应广义形态滤波器的方法，自适应选择不同尺度下的结构元素γ。

为了将系统频率响应模型一次调频反馈通道的频率信号分解成高、中、低3个频段，设计了2个串联的MMF，对输入信号进行多尺度分解。输入的信号先经前级MMF 分解得出高频信号和中低频信号；后者再经过后级MMF分别得到低频和中频信号。

2.3 多尺度一次调频控制方法实施方法

结合2.1 节的分析，将附录A 图A1 系统频率响应模型中一次调频通道上的框图替换为如图4 所示的控制框图。

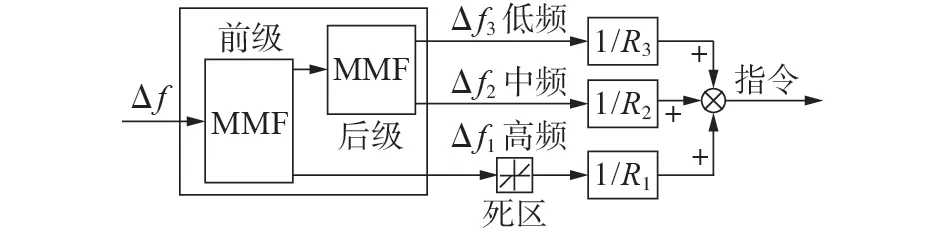
图4 多尺度一次调频控制方法Fig.4 Control method of multi-scale primary frequency regulation

图4 所示的一次调频控制方法将负反馈通道的频率信号Δf通过2.2 节的MMF 分解为高、中、低3个信号Δf1—Δf3。对于高频信号Δf1，这部分信号主要由机组惯性作用吸收掉，并在高频通道内加上了死区环节，滤除一部分高频波动，调差系数R1设为0.05；对于中频信号Δf2，此信号的频段是一次调频主要工作的频段，为了增加一次调频能力，调差系数R2的范围设置为（0.04，0.05）；对于低频信号Δf3，这个信号的频段对应二次调频作用，需要进一步增加一次调频能力，调差系数R3的范围设置为［0.03，0.04］。

为了实现信号的实时分解，本文采用滑窗滤波算法，通过一个周期内固定采样频率信号值，在每个采样点时刻都可以更新反馈通道的指令值。由于MM 方法没有乘除操作，且在时域操作不需要复杂的积分变换，因此计算量较小，一个滑窗周期造成的延时小于0.3 s，可以满足信号快速分解的要求。

3 仿真实验

3.1 仿真条件

为验证本文所提多尺度一次调频控制方法对火电机组调频能力的提高作用，在MATLAB／Simulink环境搭建如图5 所示的含风、水、火电的4 机10 节点电力系统。该系统包含2台火电机组G1与G2、1台水电机组G3、1 台风电机组。其中，风电机组不参与电力系统调频，火电机组G2与水电机组G3不参与二次调频。

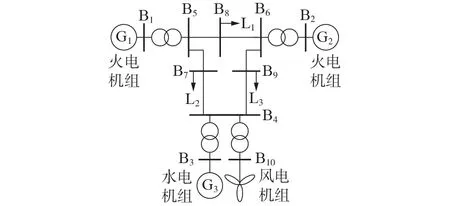
图5 修改的4机10节点电力系统Fig.5 Modified 4-machine 10-bus power system

根据华中某省实际电力系统2018 年的数据，模拟该省电力系统的实际运行状态，对本文的多尺度一次调频控制方法进行分析。系统总装机容量为2 850 MW，火电总装机容量为1 600 MW，AGC 机组G1总装机容量为1000 MW，非AGC 机组G2总装机容量为600 MW。水电机组装机容量为800 MW，风电装机容量为450 MW。

根据国家电网标准Q／GDW 669—2011《火力发电机组一次调频试验导则》，仿真中加入了火电机组出力限制，其中，1 000 MW 火电机组G1出力限制为5%，600 MW火电机组G2出力限制为6%。

多尺度一次调频策略中，调差系数R1设为0.05，R2设为0.045，R3设为0.035。

3.2 仿真结果分析

3.2.1 场景1

调频机组只启用一次调频，二次调频不动作，负荷L1、L2采用阶跃扰动的形式，负荷阶跃扰动见附录C 图C1，图中负荷波动为标幺值。火电机组G1与G2均采用多尺度动态一次调频方法，对比常规一次调频控制方法，系统频率偏差曲线如图6 所示，图中系统频率偏差为标幺值，后同。由图可知，相比常规一次调频控制方法，本文的控制方法有效地减小了频率稳态值，一次调频的动态过程也得到极大改善，这是因为当负荷为低频高幅值波动时，机组负反馈通道的频率信号多集中在为低频段，此频段信号对应的调差系数R3设置为0.035，因此整个系统的一次调频能力较强。

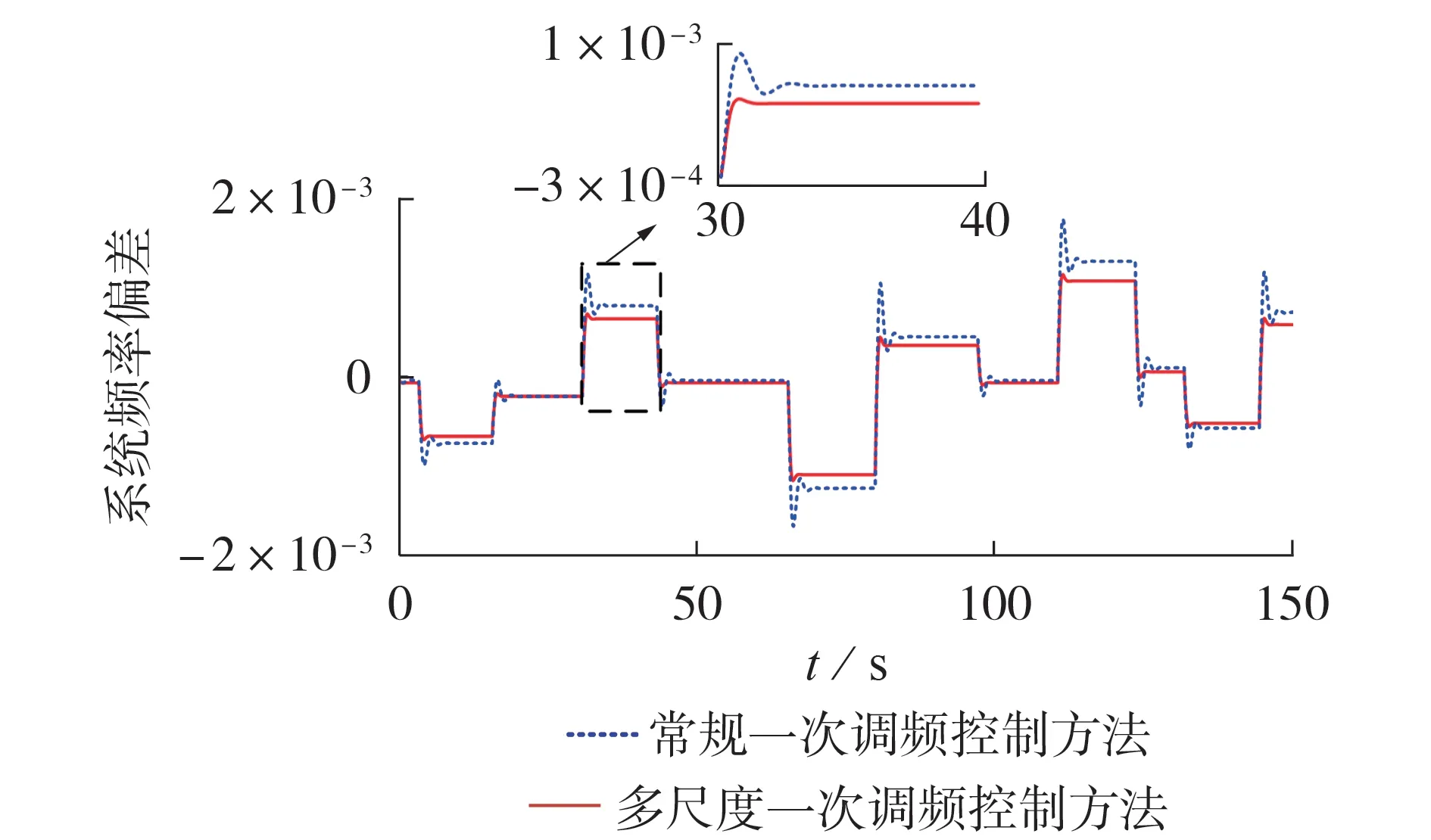
图6 阶跃扰动下电网频率偏差曲线Fig.6 Frequency deviation curves of power grid under step disturbance

3.2.2 场景2

采用实际负荷波动数据与风电出力数据，采样时间为12 000 s，采样间隔均为1 s，负荷预测采用基于实际负荷波动数据的趋势预测值并加上5%的预测误差；风电预测采用对历史数据的滑窗平均值，并加上10%的预测误差。对火电机组G1与G2均采用多尺度一次调频控制方法。负荷随机波动的最大幅值为0.01 p.u.，风电的渗透率为10%。

观察火电机组G1，该机组的一次调频负反馈通道的频率信号通过MMF 分成高、中、低3 个频段，分解效果图见附录C 图C2（a）。分解后的高、中、低3个频段信号相加，即为原信号，因此一次调频反馈通道的控制信息没有损失；MMF 有效且实时地将原信号分解成3 个频段的信号，对比原信号和低频分量信号，滤波延时仅为0.21 s，满足信号快速分解要求。

为了体现MMF 算法的快速性、准确性，附录C图C2 对比了本文所提MMF 算法、一阶惯性滤波算法、卡尔曼滤波算法和WA 算法的信号分解效果。图C2（a）中，本文的MMF 有效且实时地将原信号分解成3 个频段的信号。图C2（b）中采用一阶惯性滤波方法，可以看出此方法对于高频分量的分解效果尚可，但对中低频信号，因为算法本身具有局限性，分解效果较差。图C2（c）中采用卡尔曼滤波算法，与一阶惯性滤波算法类似，卡尔曼滤波算法的快速性尚可，但是滤波准确度较低，分解效果很差。图C2（d）中采用WA算法，WA算法本身的运算量较大，耗时较长，不能满足信号快速分解要求。可以看出，由于滤波延时长，不仅信号分解效果很差，还造成了信号混叠，控制系统失稳，造成原信号的振荡严重。

综上，正是因为本文的滤波算法本身具有滤波精度高、滤波延时较低的特点，才可以正确地将原信号分解出如图C2（a）中所示的高、中、低3个分量，而其他滤波算法如一阶惯性滤波算法、卡尔曼滤波算法和WA 算法等，都不能兼顾滤波的“准、快”的要求，因此会造成控制反馈通道的控制信息丢失，系统频率出现严重振荡现象。

对比常规一次调频控制方法，系统频率偏差曲线如图7所示。相比常规一次调频控制方法，多尺度一次调频控制方法显著改善了系统频率偏差的波动情况，频率偏差的最大值由0.065 Hz减小到0.041 Hz，频率偏差波动的方差由2.41×10-4p.u.减小为1.95×10-4p.u.，系统的一次调频能力得到了显著提高。

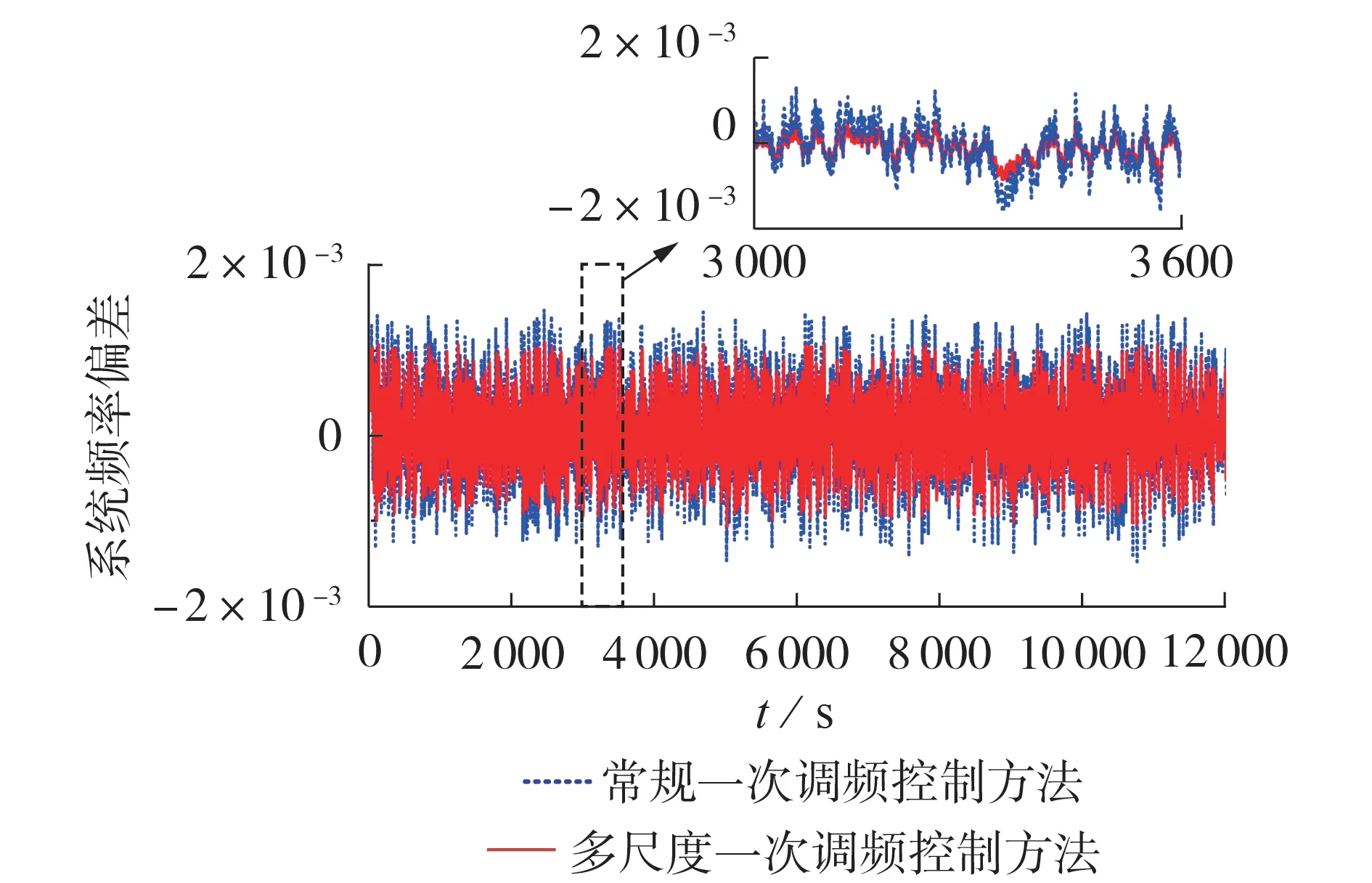
图7 实际负荷与风电连续扰动下电网频率偏差曲线Fig.7 Frequency deviation curves of power grid with actual continuous load disturbance and wind power disturbance

系统频率偏差波动的功率谱如图8 所示。采用多尺度一次调频控制方法后，系统频率偏差波动的功率谱在全频段均有所改善，系统对全频段负荷波动的调节能力均得到了一定提高。

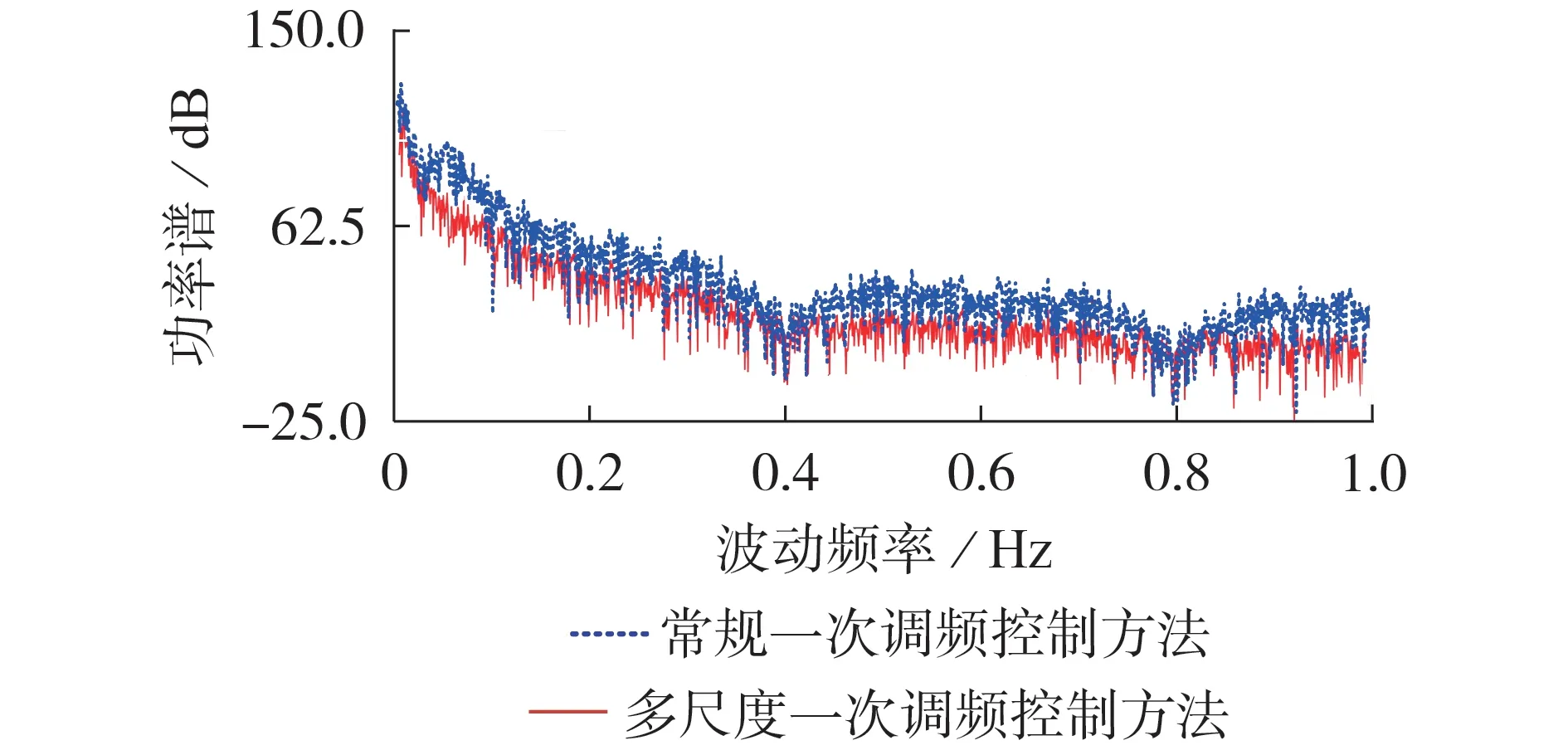
图8 系统频率偏差波动功率谱Fig.8 Power spectrum of system frequency deviation fluctuation

另外，改善前后的电网频率概率分布统计情况如图9 所示。由于常规一次调频方法中调速器死区非线性环节的存在，系统频率概率分布呈现双峰分布的情况。本文控制方法仅在高频通道内加上了死区环节，有效地将双峰分布改善为正态分布。

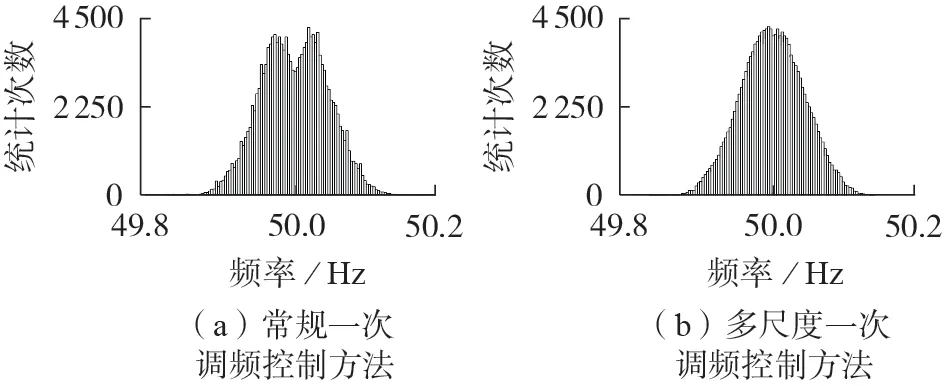
图9 系统频率概率分布图Fig.9 Probability distribution chart of power system frequency

3.2.3 场景3

为了验证本文的控制方法对高频负荷随机波动的调节能力，改变负荷波动中的高频随机波动幅值，当负荷随机波动的最大幅值ΔPLmax分别为0.02、0.03、0.04 p.u.时，3种情况下系统频率偏差曲线图见附录C 图C3，3 种情况下的频率偏差数据如表1 所示，表中频率偏差波动方差为标幺值，后同。由图C3 和表1 可知：3 种情况下，相比常规方法，改进的多尺度一次调频控制方法都有效地减小了系统频率偏差波动方差；且随着高频负荷随机波动幅值的增加，频率偏差波动方差的改善率不断增加，进一步证明了本文方法的有效性。

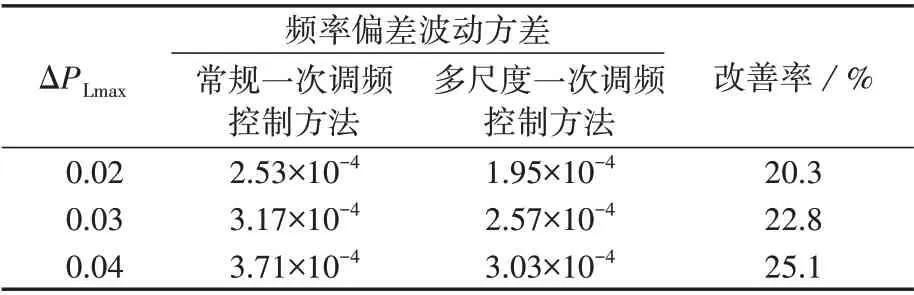
表1 3种情况下频率偏差数据Table 1 Frequency deviation data in three cases

为了验证多尺度一次调频控制方法对低频风电出力波动的调节能力，减小系统中火电机组容量，增加风电机组容量，将风电出力功率等比例增大或减小，以改变风电在系统中的渗透率。当风电的渗透率分别为20%、30%、40%时，3 种情况下系统频率偏差数据如表2所示。由表2可知，不同风电渗透率下，多尺度一次调频控制方法对系统频率偏差波动方差的改善作用明显，进而可以说明多尺度一次调频控制方法一定程度上促进了风电的发电消纳。

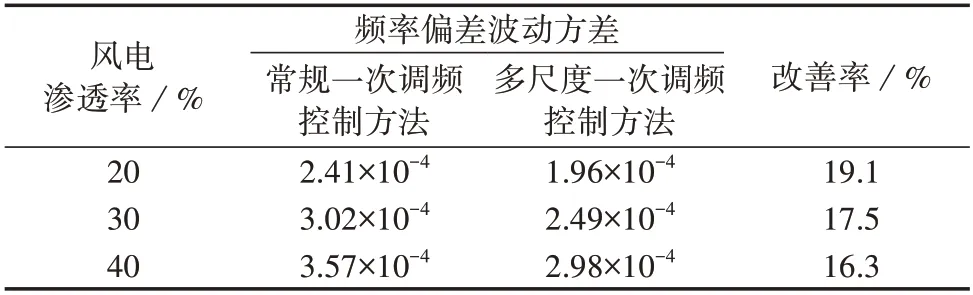
表2 不同风电渗透率的频率偏差数据Table 2 Frequency deviation data of different wind power permeabilities

随着系统中风电渗透率的不断提高，频率偏差波动方差的改善率随之减小，这是因为风电机组不参与调频，系统的调频能力随着系统中火电机组容量的减小而变弱。火电机组的频率支撑能力显著，为了最大化挖掘火电机组乃至整个系统的一次调频能力，电网中的火电机组装机容量必须有所保证。

4 结论

为了挖掘火电机组的一次调频能力，本文提出一种火电机组多尺度一次调频控制方法。该方法将原一次调频负反馈通道的频率信号通过多尺度形态学自适应滤波算法快速分解成3 个频段的信号，在不同频段信号内设置合理的调差系数，从而提高机组全频段的一次调频能力。根据电网调频模型的仿真结果，结论如下。

1）本文控制方法可以改善系统频率偏差波动在全频段的功率谱，提高机组全频段的调频能力；可以改善系统的频率概率分布。随着高频负荷随机波动幅值的增加，频率偏差波动方差的改善率不断增加。

2）本文控制方法可以一定程度上促进风电发电消纳，但随着系统中风电渗透率的不断提高，频率偏差波动方差的改善率随之减小，因此电网中的火电机组装机容量必须有所保证。

3）本文的多尺度形态学自适应滤波算法本身具有滤波精度高、滤波延时较低的优点，可以灵活应对各种场景下的负荷功率波动情况，通过分频控制，挖掘机组的调频潜力。

本文控制方法旨在以更加经济有效的方式改善当前火电机组一次调频方法的不足。理论与仿真虽能说明控制方法的有效性，但未考虑调频模型中的一些非线性环节，最终仍需要落地的工程实践来验证。

附录见本刊网络版（http：//www.epae.cn）。