钢-UHTCC组合桥面板弯曲承载性能研究*

李怀峰，刘 鑫，贺 攀，李庆华，童精中，徐世烺

(1.山东省交通规划设计院集团有限公司，山东 济南 250031；2.浙江大学高性能建筑结构与材料研究所，浙江 杭州 310058)

0 引言

钢结构具有自重轻和抗拉强度高的特点，但容易存在受压失稳及疲劳问题，因此适合做受拉构件。混凝土具有自重大、造价低、抗拉强度低和抗压强度大的特点，一般无需考虑失稳问题，适合做受压构件[1]。桥面板作为桥梁体系结构的重要组成部分，直接承受车轮荷载并将荷载传递至下部结构[2]。相较于传统的以沥青为铺装层的正交异性桥面板结构，钢-混凝土组合桥面板通过栓钉等剪力连接件将混凝土和正交异性钢桥面板连接成一个整体结构从而共同受力，让混凝土在荷载作用下受压，让钢结构部分受拉，充分发挥了两种材料各自的优势[3]。

钢桥面板多采用正交异性板，其构造复杂，纵横向加劲肋多，从而导致整个桥面板中的焊缝数量较多[4]，而焊缝中往往存在着夹渣、咬边等微观缺陷，在疲劳荷载下，容易从这些微观缺陷处衍生出裂纹，从而发生疲劳开裂现象[5]。采用混凝土作为铺装层，能够增加整体结构的刚度，降低应力幅，从而有效降低疲劳开裂的风险。采用混凝土作为铺装层还能够避免铺装层和面板之间发生脱层、推移、拥包的破坏[6]。

钢-UHTCC组合桥面板作为一种具有发展前景的新型组合桥面板结构，对其受力性能的研究至关重要，进行工程试验是研究组合结构的一种良好方法，但是成本太高[7]。因此本文利用ABAQUS有限元软件进行建模，对钢-UHTCC组合桥面板进行纵向正弯矩受力性能分析，并提出一种正弯矩作用下组合结构的承载力理论计算公式。

1 组合桥面板结构构造

新型组合桥面板结构如图1所示，由铺装层、桥面板和板式加劲肋组成，铺装层与钢桥面板之间通过剪力钉连接。铺装层采用UHTCC材料，UHTCC是一种超高韧性水泥基材料，其拉伸应变可稳定地达到3%，甚至高达6%，是普通混凝土的200～700倍，是钢筋屈服应变的10～20倍[8]。钢材采用Q355钢，UHTCC材料的力学性能参考前人研究[9]，如表1所示，钢材力学性能如表2所示。

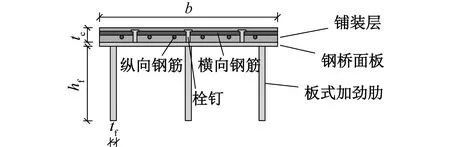
图1 新型桥面板构造

表1 UHTCC力学性能参数

表2 钢材力学性能参数

考虑到UHTCC主要受压，而受拉主要由钢结构部分承担，钢筋对组合结构的承载力和刚度较小，因此为了简化计算，忽略钢筋的作用[10]。结合实际工程可以将铺装层和钢桥面板之间视为完全连接，因此可以将图1的结构构造简化成如图2所示。这样一来影响结构承载力的设计参数包括：UHTCC层厚度tc，板肋个数nf，板肋厚度tf，板肋高度hf，桥面板宽度b。考虑到板肋宽厚比的限定，设置宽厚比hf/tf为13，因此将6个设计参数缩小成5个设计参数。

图2 组合桥面板横截面示意

2 理论极限承载力计算

正弯矩作用下，组合桥面的承载力计算遵循如下假设。

1)UHTCC与钢桥面板之间不存在滑移或滑移很小，符合平截面假定。

2)试件破坏时全截面受力且处于塑性状态。

由于中和轴位置随着设计参数的改变而改变，因此需要分成3种情况讨论：中和轴在UHTCC层中，中和轴在钢桥面板中，中和轴在板肋层中。

2.1 中和轴在UHTCC层中

中和轴在UHTCC层中的情况如图3所示，由于UHTCC具有应变硬化现象，因此假设UHTCC开裂仍不退出工作。

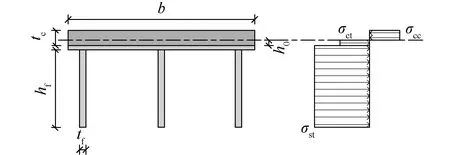
图3 中和轴在UHTCC层中的应力分布

由平衡方程：

σccb(tc-h0)=σctbh0+σstbts+σstnftfhf

(1)

得到：

(2)

从而得到极限弯矩：

(3)

式中：σcc和σct分别为UHTCC材料的抗压强度和抗拉强度；σst为钢材的抗拉强度。

2.2 中和轴在钢桥面板层中

中和轴在钢桥面板层中的情况如图4所示。

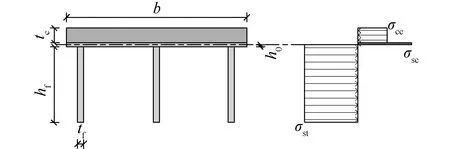
图4 中和轴在面板层中的应力分布

由平衡方程：

σccbtc+σscb(ts-h0)=σstbh0+σstnftfhf

(4)

得到：

(5)

从而得到极限弯矩：

(6)

式中：σsc为钢材的抗压强度。

2.3 中和轴在板肋层中

中和轴在板肋层中的情况如图5所示。

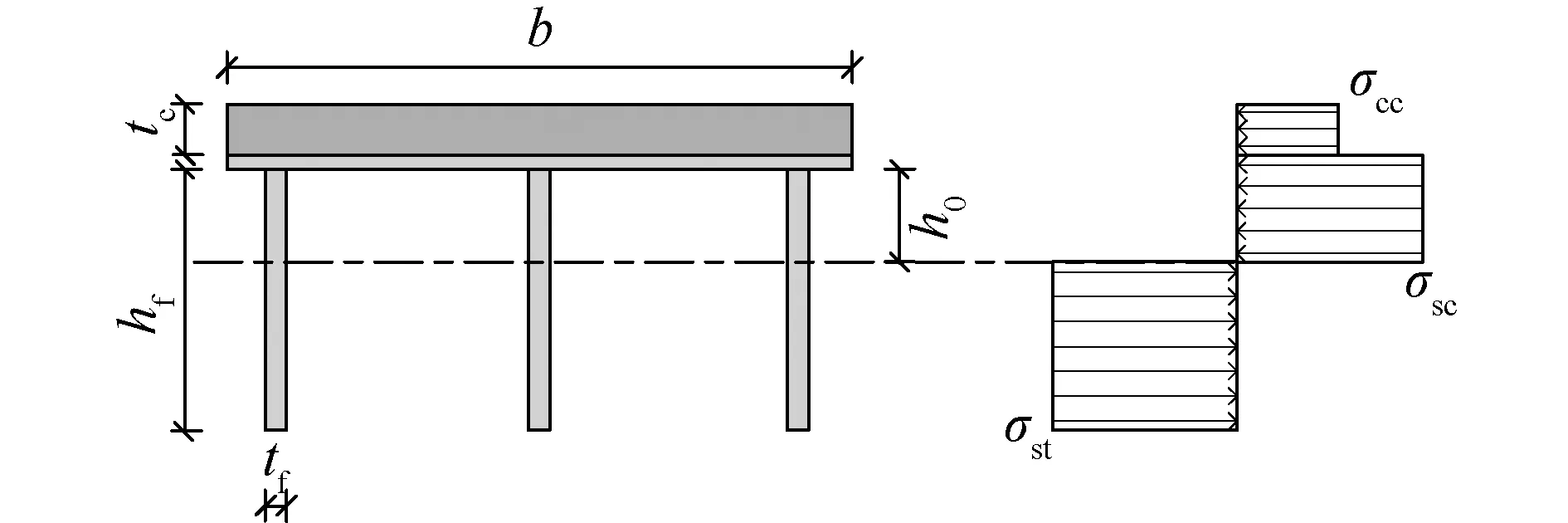
图5 中和轴在板肋层中的应力分布

由平衡方程：

σccbtc+σscbts+σscnftfh0=σstnftf(hf-h0)

(7)

得到：

(8)

从而得到极限弯矩：

(9)

2.4 极限承载力修正

在实际工程结构中，由于铺装层和钢桥面板层之间的栓钉连接难以做到完全剪力连接，因此极限承载力需要做出一定修正，结合前人的试验研究[7,10]以及有限元结果，考虑对理论承载力进行折减，折减系数取为0.9，得出实际极限承载力为

Mu，0=0.9Mu

(10)

3 理论刚度计算

刚度计算也要考虑中和轴的不同位置而分为3种情况讨论，且需满足平截面假定。

3.1 中和轴在UHTCC层中

中和轴在UHTCC层中的情况如图6所示。

图6 中和轴在UHTCC层中的截面应变

由平衡方程：

(11)

得到：

(12)

从而得到：

(13)

式中：Ec和Es分别为UHTCC和钢材的弹性模量；αc为Ec/Es。

3.2 中和轴在钢桥面板层中

中性轴在钢桥面板层中的应变分布如图7所示。

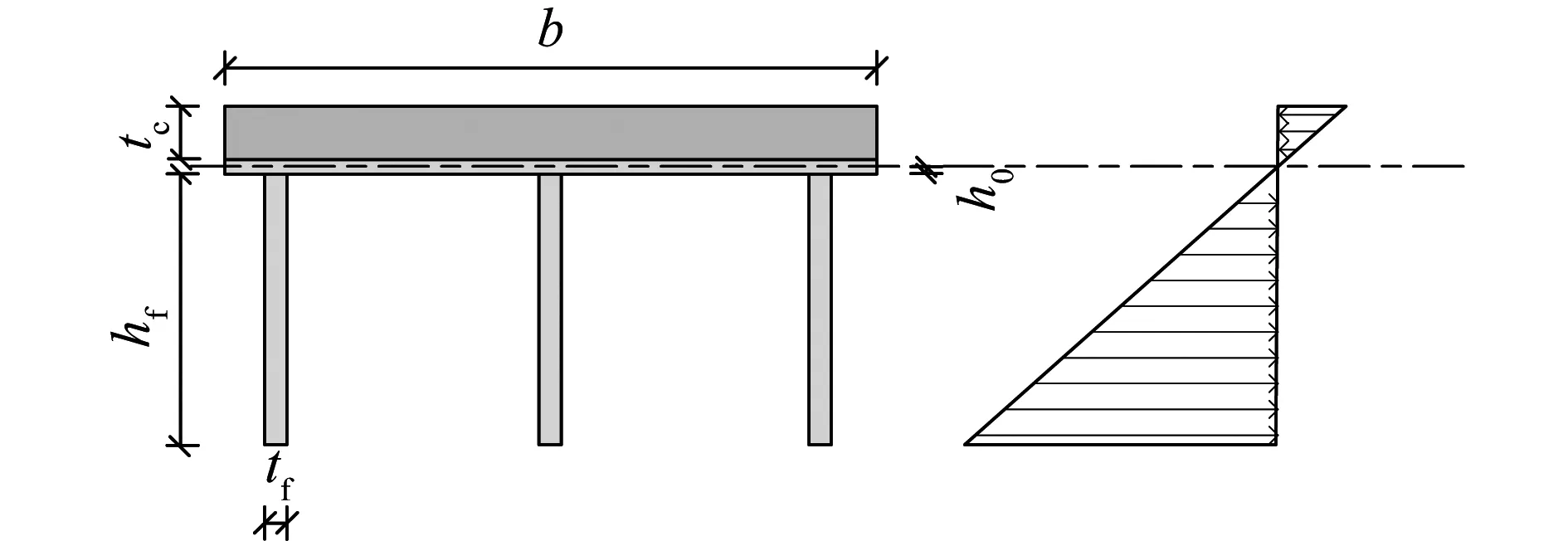
图7 中和轴在桥面板层中的截面应变

由应力平衡方程：

(14)

得到：

(15)

从而得到：

(16)

3.3 中和轴在板肋层中

中性轴在板肋层中的情况如图8所示。

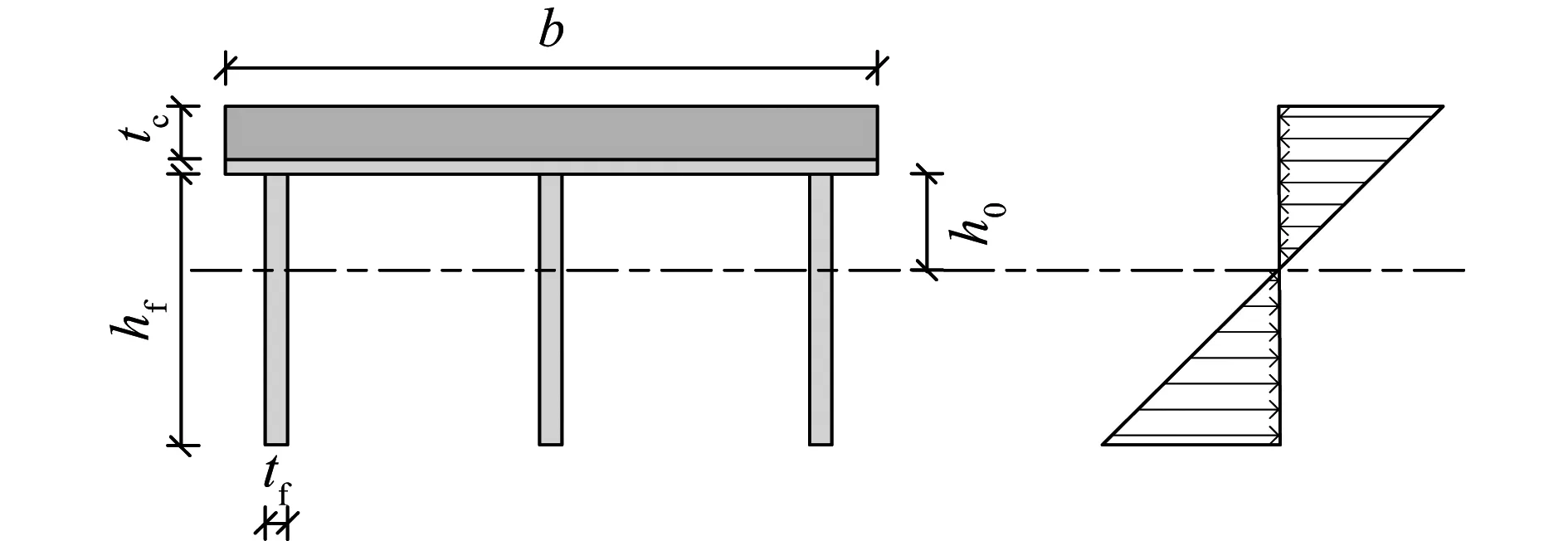
图8 中和轴在板肋层中的截面应变

由应力平衡方程：

(17)

得到：

(18)

从而得到：

(19)

4 有限元模拟

利用ABAQUS建立有限元模型，模型的总长为3.2m，宽为0.5m，如图9所示。

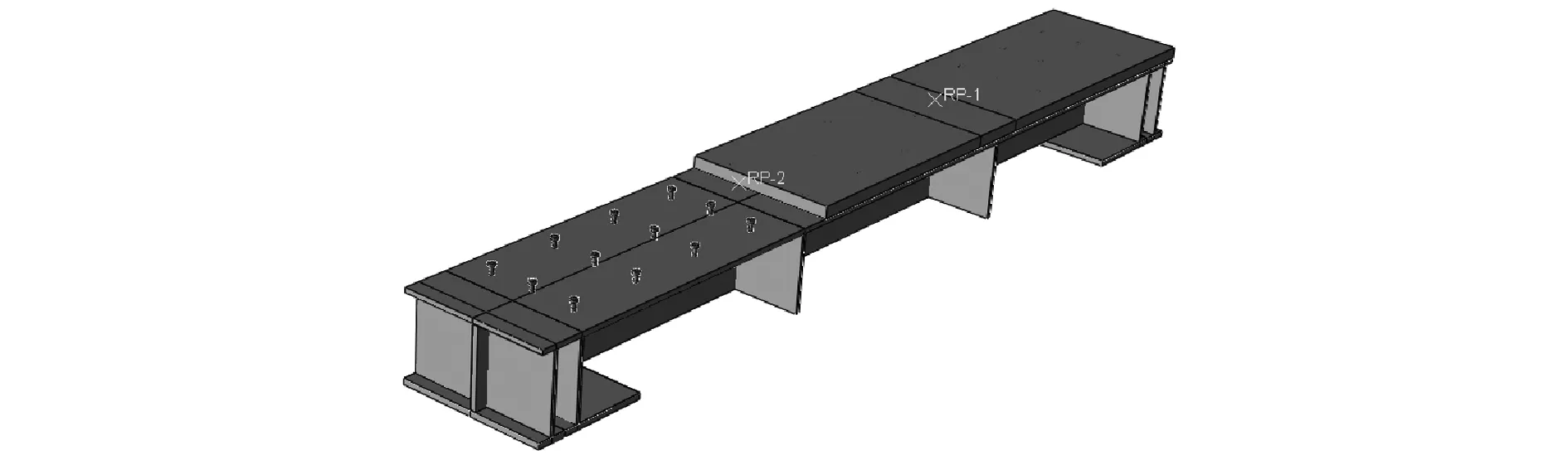
图9 有限元模型

模型包括UHTCC层，栓钉和下部钢结构部分，其中UHTCC层和栓钉都采用实体单元C3D8R，桥面板及板肋采用壳单元S4R。接触方式定义为：栓钉上部嵌入UHTCC层中，底面与钢桥面板采用绑定约束，UHTCC底面与桥面板设置法向硬接触，切向摩擦系数设为0.2[11-12]。加载方式采用四点弯加载，两边设置简支约束，具体的加载形式如图10所示。

图10 四点弯加载示意

设置的模型组如表3所示。

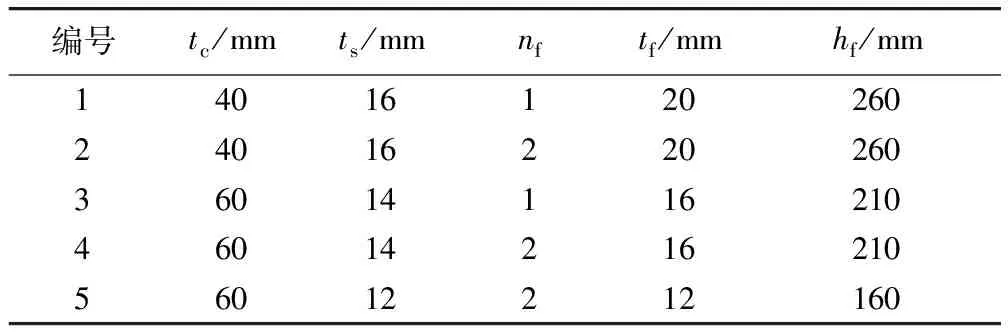
表3 模型对照组

有限元计算得到的荷载位移曲线如图11所示，荷载为单个加载点的荷载，位移为跨中位移，由于理论计算值使用的是截面刚度EI，荷载位移曲线得到的是原点切线的斜率，也即荷载与位移的比值，因此需要根据如下的简支梁跨中挠度曲线公式进行转换：

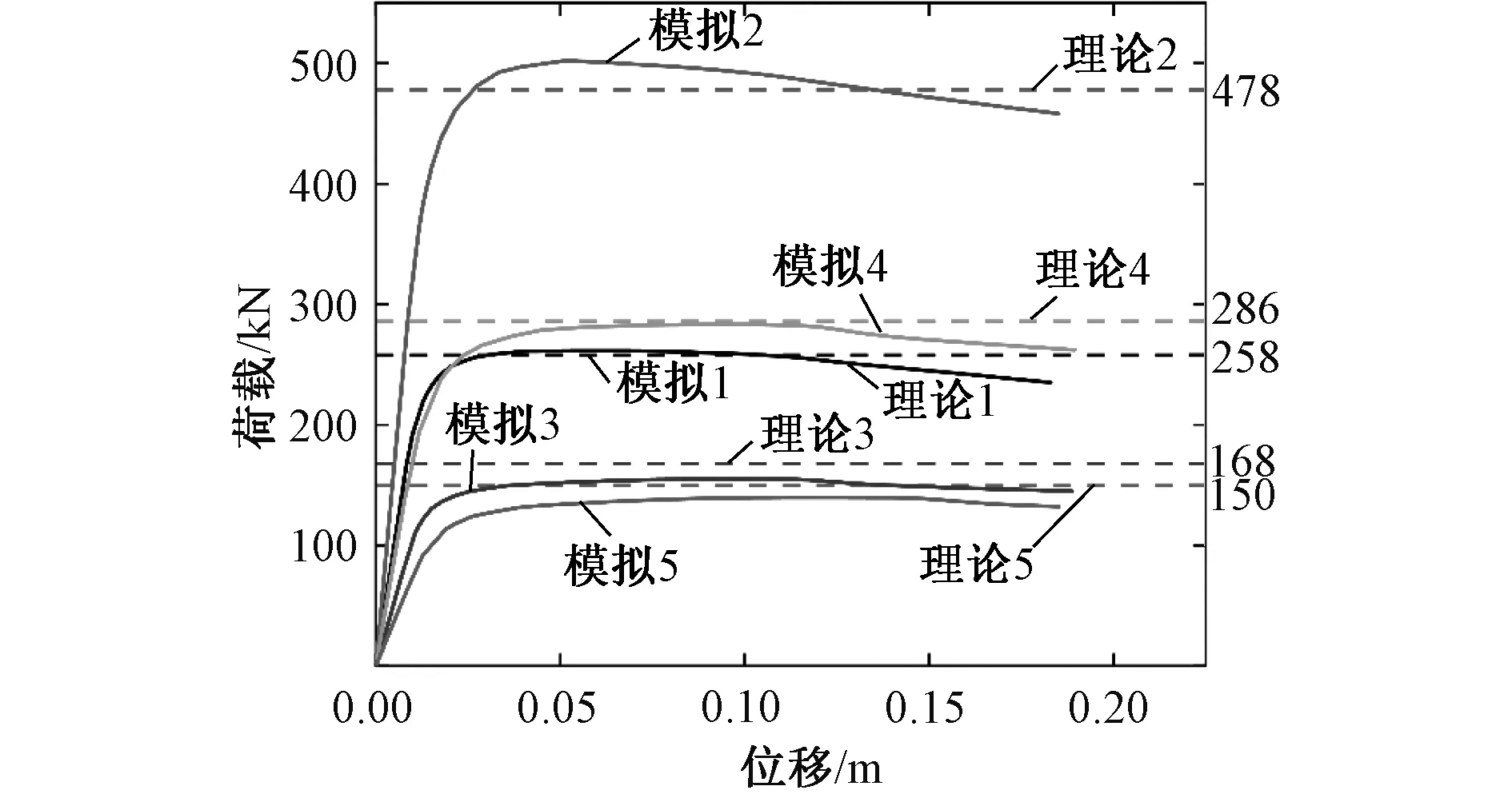
图11 有限元计算荷载位移曲线

(20)

式中：l和a分别为简支梁净跨和加载点距离支座的距离。

根据图10可以得到理论承载力F和Mu的关系：

Mu,0=F

(21)

理论计算值和有限元计算结果如表4所示。从表4可以看出，有限元计算结果和理论公式计算结果误差不大，有限元计算得到的承载力与理论公式误差均在10%以内，有限元计算得到的刚度与理论公式计算得到的刚度吻合程度都在95%以上，这验证了理论公式计算结果的正确性和适用性。

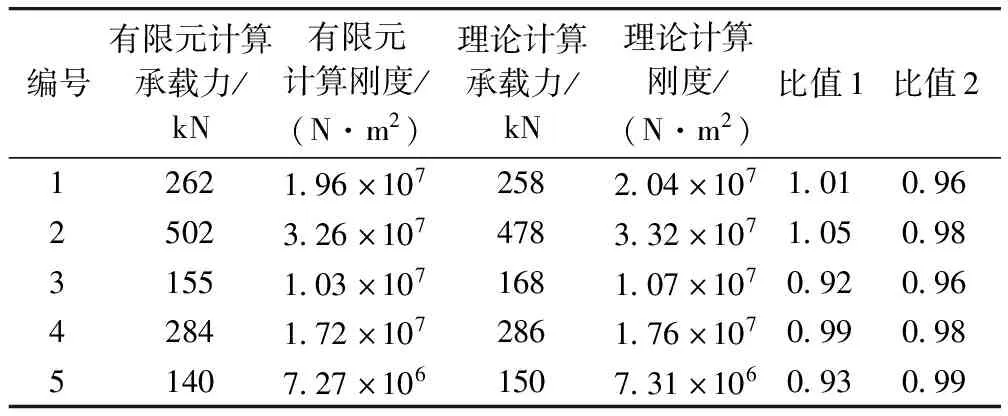
表4 计算结果

5 结语

基于破坏状态下全截面处于塑性状态的假定以及平截面假定，本文针对UHTCC-钢新型组合桥面板结构进行了正弯矩作用下承载力和刚度的理论公式推导，并与有限元计算结果进行了比较。结果表明，本文提出的理论公式计算结果与有限元计算结果基本吻合，理论计算的承载力与有限元计算结果误差均在10%以内，有限元计算得到的刚度与理论公式计算得到的刚度吻合程度都在95%以上，说明了这种计算方法的可靠性。