机载往复密封二元时变相关退化建模与可靠度评估

柏文峰， 洪 黎， 张 超， 钱于杰

(1.中国航发控制系统研究所， 江苏 无锡 214100； 2.北京航空航天大学 自动化科学与电气工程学院， 北京 100191)

引言

航空工业是一个国家科技水平、工业能力和综合国力的集中体现，液压技术因其驱动功率密度大、快速性好、刚性大等优点，已经在航空领域得到广泛的应用[1]。往复密封件作为机载液压系统作动器的重要组成部分，其性能和可靠性会直接影响飞机的整体性能与安全。液压往复密封件主要受密封耦合面的润滑、摩擦、磨损、材料性质以及结构设计原理的影响，其中密封耦合面间的摩擦将导致密封件表面材料的丧失和迁移，导致密封件的磨损，影响其使用寿命[2]。航空液压作动器工况复杂，压力、温度、作动速度、频繁的振动、多变的载荷状态等严酷的机载环境对往复密封件的性能都具有较高的要求。

国内外对于往复密封的失效机理进行了大量的理论和试验研究。针对往复密封的理论研究，主要采用弹性方程和流体雷诺方程。SALANT R F等[3]利用正向求解雷诺方程的方法建立活塞杆往复密封的数值模型。欧阳小平等[4]通过求解考虑空化及流动因子的雷诺方程，建立了基于混合润滑理论的往复密封多场耦合模型。国内对于往复密封的研究对密封件建立数值模型并进行有限元分析[5-6]，同时也进行了往复密封的试验研究[7-9]。对于机载高压、宽温、强振动、变载荷等恶劣工况，单纯依靠失效物理、数值迭代或工程经验建模分析已经无法准确地描述往复密封件的实际工作情况。

近年来，基于随机过程的退化过程建模逐渐成为了研究热点，维纳过程[10-11]、伽马过程[12-13]和逆高斯过程[14-15]都是主流的随机退化过程。维纳过程可以灵活地描述各种系统的退化指标，且结果令人满意，因此维纳过程最近受到较多的关注。国内外大量的关于电子元件、机械元件的性能退化建模基于随机过程方法进行研究，这对往复密封件的性能退化分析及可靠性建模提供了理论支撑。

工程实际中，机电产品不止1个性能退化指标。若仅考虑1个性能指标，退化过程建模不准确或者不精确。Copula函数因其优良的特性，已经被广泛应用于金融、风险管理等领域。近些年来，Copula函数逐渐被学者引入可靠性评估与寿命预测领域，用于描述多个部件之间失效模式的相关性或者多个物理量之间的相关性等。ARMA表达是时间序列分析常用的模型。WANG等[16]采用ARMA(1,10)模型表征Copula函数的时变相关性系数，解决多个相关退化量之间的时变相关性问题。PAN J等[17]针对密封件贮存时2个退化量相关性分析，使用ARMA模型考虑其相关性系数随时间变化的规律，并得到相关的可靠性信息。

综上，为了解决高压、宽温、强振动、变载荷等恶劣工况条件下机载往复密封的可靠性评估难题，本研究建立基于ARMA模型的机载往复密封二元时变相关退化模型，基于维纳过程分别建立往复密封的摩擦力和泄漏量的退化模型，采用Copula函数解决2个性能退化指标之间的相关性问题，采用ARMA模型表征相关性系数随时间的变化。在模型求解时，采用2段贝叶斯参数估计的方法进行参数估计，基于马尔可夫链蒙特卡洛循环(MCMC)的方法对往复密封的可靠性进行评估。

1 基于维纳过程的往复密封退化模型

1.1 往复密封原理

图1为往复密封的原理图，密封件被安装在特定的密封腔中，起到阻止油液泄漏的作用，在外侧还安装有防尘圈，起到辅助密封和防止外界杂质进入的作用。当活塞杆向液压缸外侧伸出(外行程)时，液压油会被活塞杆拖拽至外部环境，造成油液泄漏及环境污染；当活塞杆向液压缸内侧收回(内行程)时，一些油液会被带回液压缸内，同时外部的粉尘微粒、空气等杂质被带入液压缸，导致密封件的磨损以及油膜的破裂。活塞杆往返的2次轴向运动，形成1个工作循环，活塞杆表面的润滑油膜会随往复运动而不断变化。

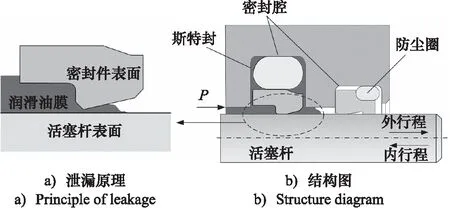
图1 往复密封原理图Fig.1 Principle diagram of reciprocating seal

机载往复密封件工况复杂，摩擦力、泄漏量、接触区域温度、磨损量等都是其性能退化指标，皆可反映往复密封件的性能退化，且互相耦合。相关研究表明，摩擦力和泄漏量是反映往复密封件状态的最重要的2个性能退化指标。往复运动过程中，润滑油膜不仅起到密封作用，同时也会对密封件所受摩擦力和泄漏量产生一定影响。摩擦生热会使油膜温度升高，油液黏度降低，泄漏量会增加，油膜承载力降低，反过来也会影响摩擦力大小。同时，摩擦力的增加也会导致密封件磨损量的增加，进而导致泄漏量的增加。由此可知，往复密封件所受摩擦力和泄漏量之间相互关联，相互耦合，相互影响，因此考虑摩擦力与泄漏量这2个性能退化指标。

1.2 基于维纳过程的往复密封退化建模

维纳过程适用于因微小修复、自我修复或降低使用强度而导致的非单调退化过程。因此，基于维纳过程的退化建模已经广泛应用于机械部件、电子产品等领域的可靠性评估与寿命预测中，且取得了较为丰富的研究成果。本研究假定往复密封件的退化过程服从维纳过程。

令{Xk(t)，t≥0}，表示密封件第k个性能退化指标在t时刻的退化量，其中k取1或2。假定这2个性能退化指标的退化过程服从非线性维纳过程，可表示为：

{Xk(t)=μkΛk(t)+σkW(Λk(t))，t>0}

(1)

式中，μk为第k个性能退化量的漂移参数，用于描述退化速率；σk为第k个性能退化量的扩散系数，用于描述退化过程的随机性；W(·)为标准布朗运动；Λk(t)是时间尺度变换函数，用于描述第k个性能退化量的退化轨迹。

机载工况下，往复密封件的退化过程受作动器作动距离、速度、频率等影响。本研究进行的试验主要针对恒定应力，因此基于维纳过程建立退化模型时，退化速率μk、扩散系数σk在整个退化过程中保持不变，假设漂移参数和扩散参数的时间尺度变换函数满足时间的幂指数关系，即Λk(t)=tqk。

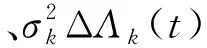
(2)

式中, ΔΛk(t)=Λk(t+Δt)-Λk(t)。

第k个性能退化指标在t时刻的退化量ΔXk(t)的分布函数Fk(ΔXk(t))满足：

(3)

式中，Φ(·)为标准正态分布。

设Dk为密封件的第k个性能退化指标对应的失效阈值，即若Xk(t)≥Dk，则认为密封件失效，密封件寿命Tk可表示为：

Tk=inf{t,Xk(t)≥Dk}

(4)

其中，Tk的失效概率密度函数为：

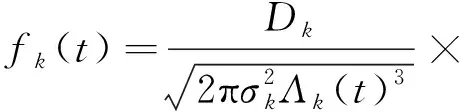
(5)

其累积分布函数为：

(6)

式中，fk(u)为Tk失效概率密度函数。

综上可得产品的可靠度函数Rk(t)为：

Rk(t)=1-Fk(t)

(7)

若共有N个密封件进行退化试验，Xk(tij)表示第i个密封件的第k个性能退化指标在tj时刻的退化量，退化增量为ΔXk(tij)=Xk(tij)-Xk(ti(j-1))。对于任意的第i个密封件，在互不重叠的时间区间内，2个性能退化指标的退化增量之间互相独立；仅当在相同的时间区间内，2个性能退化指标的退化增量具有相关性，可用Copula函数来表征这种相关性。

2 往复密封二元时变相关退化模型

2.1 基于Copula函数的相关退化建模

Copula函数连接起2个边缘分布函数，更加灵活，因此近年在可靠性领域得到了广泛的应用。为了解决往复密封件的多个性能退化指标之间的相关性问题，采用Copula函数表示多个性能退化指标之间的相关性。

利用二元Copula函数研究摩擦力和泄漏量的相关性可分为2个阶段，第一阶段先分别计算摩擦力和泄漏量各自的边缘分布函数，第二阶段将摩擦力和泄漏量的边缘分布函数作为Copula函数的输入，由此可简化计算。采用Frank Copula函数来表征往复密封摩擦力与泄漏量之间的相关性关系，Frank Copula函数的分布函数为：

(8)

概率密度函数为：

(9)

用Copula函数来分析第i个密封件的摩擦力和泄漏量之间的相关性，其具体形式由式(10)给出：

H(ΔX1(tij),ΔX2(tij))

=C(F1(ΔX1(tij)),F2(ΔX2(tij));θi)

(10)

式中，θi为Copula函数在描述第i个密封件的摩擦力和泄漏量之间相关性系数。考虑到不同密封件个体间的差异，每个密封件对应的相关性系数θi不同。若共有N个密封件进行退化试验，则可得到N个Copula函数的相关性系数(θ1,θ2…,θN)[18]。

假设D1，D2分别为2个性能退化指标的阈值，任意一个退化量X1(t)或X2(t)超过各自对应的阈值时即认为失效，基于此假设往复密封件的可靠度函数R(t) 可以表示为：

R(t)=P{X1(t)≤D1,X2(t)≤D2}

(11)

2.2 基于ARMA模型的时变相关性系数建模

传统的基于Copula函数的二元相关退化过程模型中，用以描述2个性能退化指标的相关性关系的Copula函数参数θ一般被视为常数，其表示的物理意义是该系统的2个性能退化指标之间的相关性关系不随时间改变。在工程实际中，随着环境与自身条件不断改变，2个变量之间的相关性关系往往随时间不断变化。往复密封件在往复运动过程中，外界工况不断变化，且密封件自身状态也随时间变化，因此考虑2个性能退化指标之间的时变相关性。

针对这一问题，将Copula函数的时变相关性系数用ARMA模型表达，并用常数作为对比，建立基于Copula函数的往复密封二元时变相关退化模型。假设相关性系数θ满足ARMA(1,10)模型，其数学表达式如下：

(12)

式中,uij=F1(ΔX1(tij))，vij=F2(ΔX2(tij)),Γ(·)为转换函数，保证参数在定义域内。

综上所述，由式(2)、式(10)和式(12)得到基于ARMA的机载往复密封二元时变相关退化模型：

(13)

3 参数估计与可靠度评估

3.1 基于贝叶斯方法的参数估计

由Copula函数的特点可将基于ARMA的机载往复密封二元时变相关退化模型求解分为2个独立的阶段：第一阶段分别求解往复密封件摩擦力、泄漏量各自的一元退化过程，对应的2个维纳过程参数为α=(μ1,σ1,q1,μ2,σ2,q2)；第二阶段求解往复密封件的摩擦力和泄漏量之间的时变相关性关系，对应的ARMA模型参数为θ=(ωθ,βθ,αθ)。本研究采用贝叶斯参数估计的方法进行参数估计。

上述基于ARMA模型的机载往复密封二元时变相关退化模型的对数似然函数表示为：

(14)

式(14)给出的数似然函数L(α,θ)可视为2个似然函数的相加，两部分分别对应于模型求解的2个阶段。摩擦力和泄漏量退化过程的对数似然函数和具有时变相关性系数的Copula函数的对数似然函数分别表示为：

(15)

通过式(15)，结合贝叶斯参数估计的方法可分别估计出退化过程参数α和随机相关参数θ。

第一阶段估计2个维纳过程的参数α，其数学表达式如下：

P(α|ΔXk(tij))∝π(α)×L(ΔXk(tij)|α)

(16)

式中,P(α|ΔXk(tij))为后验分布，π(α)为先验分布，取无信息先验分布。在得到参数α的估计值以后，结合式(3)计算摩擦力和泄漏量各自的边缘分布函数F1(ΔX1(tij))和F2(ΔX2(tij))的值。

第二阶段估计先将第一阶段求得的摩擦力和泄漏量的边缘分布函数F1(ΔX1(tij))和F2(ΔX2(tij))作为Copula函数的输入量uij和vij，然后估计满足ARMA模型的Copula函数时变相关性系数的参数θ，其数学表达式见式(17)：

P(θ|(uij,vij))∝π(θ)×L((uij,vij)|θ) (17)

式中,P(θ|(uij,vij))为后验分布；π(θ)为先验分布，取无信息先验分布。

OpenBUGS是英国剑桥大学研究的一款贝叶斯统计分析的软件，本研究有关贝叶斯参数估计部分将由OpenBUGS软件计算。

3.2 可靠度评估

根据维纳过程、Copula函数、ARMA模型建立的基于ARMA的机载往复密封二元时变相关退化模型，其根本目的是通过该模型计算往复密封件的可靠度，以指导实际工程应用。仅考虑1个性能退化指标时，可靠度计算较为简单，例如对于服从维纳过程的退化模型，由式(7)可得其可靠度。当有多个性能退化指标时，若多个退化量之间互相独立，可分别计算每个退化量的可靠度；若多个退化量之间相关，则不能直接单独计算，其可靠度计算也较为复杂。由二元相关退化模型可靠度计算的基本原理出发，采用基于马尔可夫链蒙特卡洛循环的可靠度计算方法。

考虑摩擦力与泄漏量，这2个退化指标中任意1个超过其失效阈值，则判定往复密封件失效。往复密封件可靠度R(t)的物理意义是：t时刻密封件能够正常工作的概率，即t时刻之前摩擦力与泄漏量的最大值均小于其失效阈值D1和D2的概率。

4 机载往复密封试验装置与模型验证

4.1 机载往复密封试验装置

往复密封多场耦合动态演化试验装置通过模拟实际机载工况，对往复密封件进行应力加载，对其所受的摩擦力以及泄漏量在线监测，以验证上述所提出的模型并对往复密封的可靠性进行评估，往复密封试验装置的结构如图2所示。在本研究中，摩擦力和泄漏量的数据将被采集，用来验证所提出的模型，并对往复密封件的可靠性进行评估。

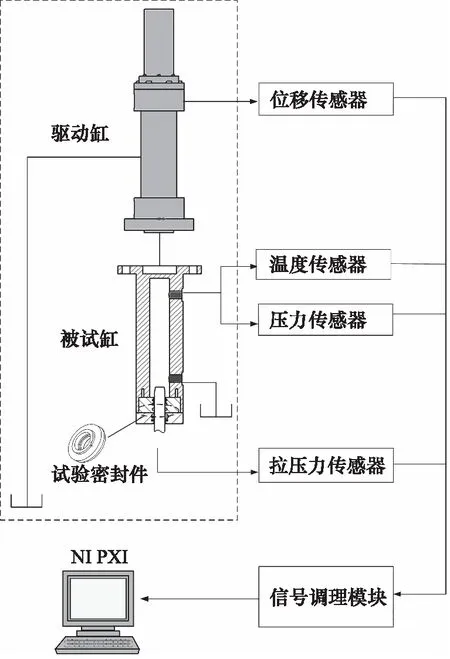
图2 往复密封试验装置结构图Fig.2 Structure diagram of reciprocating seal test device

往复密封试验装置的三维图如图3所示，试验装置整体采用立式结构布局。相对于卧式结构，立式结构处可以避免由活塞杆重力导致的密封件两侧受力不相等的情况，减小附加摩擦。往复密封试验装置的主要部件从上到下依次为驱动缸、被试缸、活塞杆和拉压力传感器，其中驱动缸固定在主体台架上，其余机构通过连接板安装于滑动导轨上，可上下移动，拉压力传感器用于测量往复密封件所受到的摩擦力。

图3 往复密封试验装置三维图Fig.3 Three-dimensional diagram of reciprocating seal test rig

被试密封件安装于被试缸下端，为了便于对密封件进行更换，设计了如图4所示的密封件更换装置。密封件工装模块内部有3个密封件安装槽，可单个安装不同样式的密封件，也可进行组合密封试验。防尘圈工装模块内安装防尘圈，防止杂质进入试验缸；侧壁开孔作为泄漏油液的流出通道，用以测量往复密封的泄漏量。针对不同直径的密封件，可采用不同内径的密封件工装模块与防尘圈工装模块，提高往复密封试验装置的通用性。

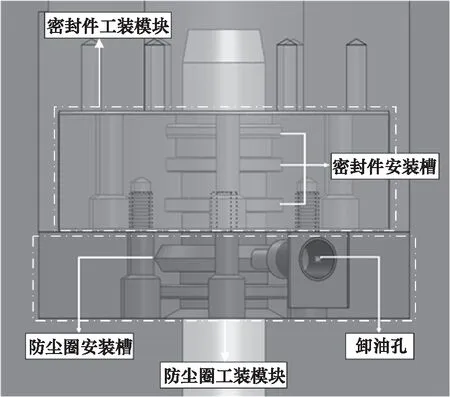
图4 密封件更换装置Fig.4 Seal replacement device

在被试密封件安装好以后，调整活塞杆的位置，使得活塞杆与被试密封件之间保持同轴度且与滑动导轨平行，以避免因偏心产生的附加摩擦，最后通过螺栓将下方连接板固定台架上。驱动缸带动被试缸沿着滑动导轨往复运动，滑动导轨的存在，保证了往复运动过程中活塞杆与被试密封件之间的同轴度。

4.2 参数估计与可靠度评估验证

本研究共对8个密封件进行了长达500 h的试验，其中4组样本的摩擦力与泄漏量退化轨迹如图5所示。

图5 摩擦力与泄漏量退化轨迹Fig.5 Degradation of friction and leakage

根据3.1节提出的模型解算方法，可先进行第一段贝叶斯参数估计，确定密封件摩擦力和泄漏量各自的一元退化过程，即2个维纳过程的参数α=(μ1,σ1,q1,μ2,σ2,q2)。由OpenBUGS软件估算可得各参数的分布如图6所示，其估计值在表1中列出。将维纳过程参数的估计值与退化增量带入式(3)，求得2个退化增量的分布函数，并作为二元Copula函数的输入。

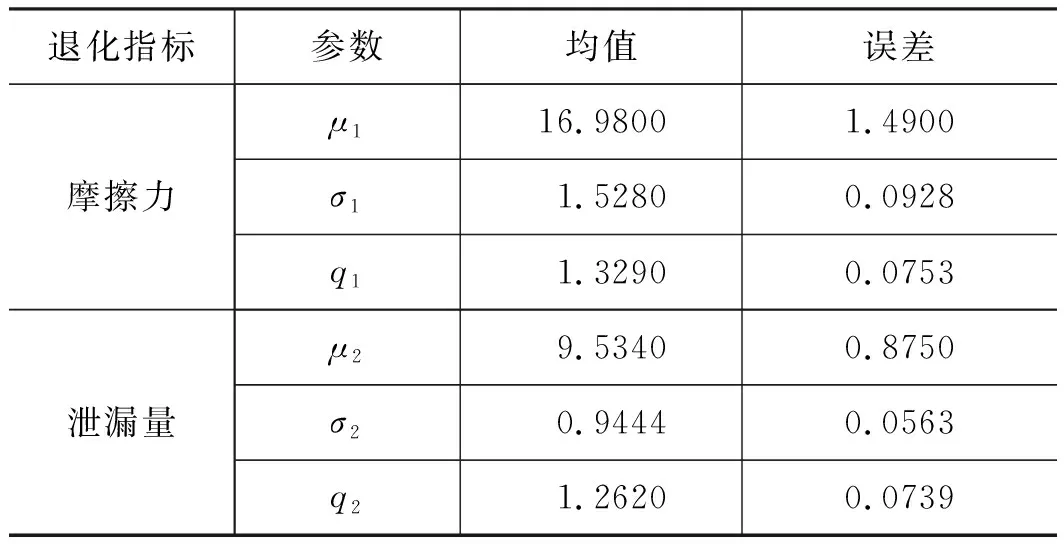
表1 维纳过程各参数估计值

第二段贝叶斯参数估计，用以确定Frank Copula函数相关性系数的ARMA表达式参数，即θ=(ωθ,βθ,αθ)。由OpenBUGS软件估算可得各参数的分布如图7所示，其估计值在表2中列出。

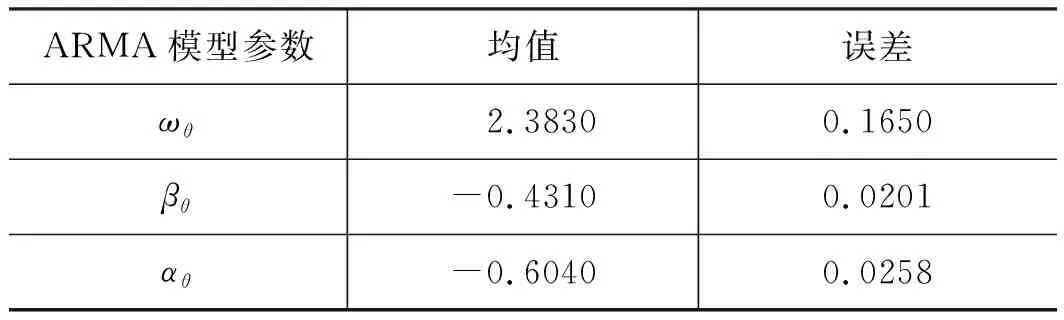
表2 ARMA模型各参数估计值Tab.2 Estimated values of parameters in ARMA model

图6 维纳过程参数分布Fig.6 Distributions of parameters in Wiener process

图7 ARMA模型中各参数的分布Fig.7 Parameter distribution in ARMA model

根据表1和表2中对于模型参数的估计结果，结合式(7)和式(11)，对往复密封件的可靠性进行评估。分别对仅考虑泄漏量指标、仅考虑摩擦力指标、考虑摩擦力与泄漏量之间的相关系数为常数和摩擦力与泄漏量之间满足ARMA时变相关这4种情况的往复密封件进行可靠性评估，结果如图8所示。

从图8中可以看出， 在仅考虑泄漏量或摩擦力的情况下，往复密封件的可靠度会高于综合考虑两者具有相关性时的可靠度，其原因是，存在某一个性能退化

图8 可靠度曲线Fig.8 Reliability curve

指标达到阈值时，另一性能退化指标可能早已达到失效阈值。在摩擦力和泄漏量2个性能退化指标中，摩擦力更能反映往复密封件的失效。

5 结论

提出了一种基于ARMA模型的机载往复密封二元时变相关退化模型，往复密封摩擦力和泄漏量退化轨迹用维纳过程描述，采用Copula函数表示2个性能退化指标之间的相关性，并用ARMA模型表征相关性系数的时变性。采用两段贝叶斯估计的方法对模型中的参数进行估计。最后介绍了往复密封试验装置，并基于此装置的试验数据验证了提出的退化模型，试验结果验证了所提出的往复密封退化模型的准确性。