调节阀附加耦合负载的形成机制

潘子晗， 谢玉东， 韩家桢， 王 勇

(1.山东大学 机械工程学院， 山东 济南 250061；2.山东大学 高效洁净机械制造教育部重点实验室， 山东 济南 250061)

引言

舰船调节阀是指在舰船的核动力装置的核岛、常规动力装置及其辅助控制系统的蒸汽等流体输送中起调节作用的阀门。舰船调节阀控制着动力系统的启动、停止和功率输出，其结构如图1所示。执行机构根据控制器的信号，通过阀杆带动阀芯，改变阀芯和阀座间的通流面积，从而控制调节阀的流量或压力。调节阀动态特性高度非线性，在一定条件下，阀内流体的动能和压力能发生转换，造成流量和压力波动。在舰船实施复杂的动作时，调节阀处于启动、关闭、调整的动态过程中，流体的振荡与阀内构件形成非定常的流固耦合效应，振荡的流体载荷给执行机构造成附加耦合负载。附加耦合负载与调节阀原有的负载叠加后，有可能使阀门所需的驱动力矩大于执行机构输出的最大力矩，导致执行机构不能动作或动作异常，使调节阀失去调节能力。如果载荷继续增大，则有可能造成阀门部件受损，进而影响舰船的航行。

图1 调节阀结构示意Fig.1 Diagram of control valve

近年来，一些研究者对有关调节阀流体负载开展了研究。廖瑶瑶等[1-3]采用CFD仿真模拟的方法，研究了不同阀口形态下阀芯所受液动力及动态特性。彭健等[4-7]建立了调节阀内部流场的计算模型，用流固耦合仿真分析和探讨不同条件下各级压降特性以及空化对阀门的影响。陈雨洋等[8]建立了水击卸压阀运动时的数学模型，在AMESim软件中模拟实际水击现象，分析动态特性。AHUJA V等[9-10]对阀门进行了非定常流动仿真并计算动态负载。HAN等[11]用AMESim-Fluent联合仿真模拟调节阀运动，对其流体振荡进行数值分析。汤志勇等[12-13]推导得出了锥阀动态液动力的计算公式，研究了液动力在低频和高频下的频率响应，并进行实验验证。SORENSEN等[14]对不同阀座液压阀的液动力进行了数值分析。郑淑娟等[15]对运动状态的液压锥阀流场作了仿真分析。

目前，对于舰船用调节阀等非液压系统调节阀以及其附加耦合负载的国内外相关研究较少。为了使舰船在执行任务时其动力系统不会因调节阀而发生故障，本研究通过对调节阀的有限元建模，设置调节阀阀芯移动方向、不同的突变压力值及阀芯运动速度，分析每组仿真的阀芯轴向受力及压力情况，讨论调节阀在不同外界突变压力、不同阀芯调节速度下的附加耦合负载状况；以探究调节阀在动态调节中附加耦合负载规律，为动态负载的补偿提供基础规律，并为舰船调节阀的安全稳定运行提供参考。

1 仿真方法

1.1 仿真模型的建立及网格划分

本研究选用一种线性流量特性的调节阀建立仿真流道模型，其阀腔及周围纵剖示意如图2所示，其具体参数见表1。本研究建立了2个调节阀流道模型进行流体仿真，阀芯分别处于起始开度40%与起始开度100%的2个位置，模拟舰船调节阀在不同行程下控制流体的过程。起始开度40%，阀芯从下向上移动，开度增大，以研究在调节阀调节至50%左右调节阀内部的负载变化；阀芯的起始开度100%，阀芯从上向下移动，开度减小，以研究阀门在大开度向下调节时调节阀内部的负载变化，网格模型如图3～图4所示。

图2 调节阀流道模型部分纵剖示意

图3 调节阀流道网格模型Fig.3 Grid model of flow passage in control valve

图4 调节阀阀芯周围纵剖网格模型Fig.4 Longitudinal grid model around control valve spool

表1 调节阀模型参数Tab.1 Parameters of control valve model mm

1.2 仿真参数的设置

为了分析流体和阀芯运动等不同条件的变化对阀门所受负载的影响，仿真设定阀芯运动速度变化和突变压力变化两类工况，分别进行具体的自定义函数设置。

仿真通过使管路内的压力突变来模拟舰船在运行时战术动作的突然转换，主要设置网格模型中入口压力这一边界条件的变化规律。本研究设置的压力变化规律如图5所示，压力最大值pmax取5，13，17，21 MPa 4种情况，在仿真开始0.06 s后施加突变压力并瞬间达到最大值pmax，持续0.04 s后瞬间恢复至原来的压力。

图5 调节阀仿真压力变化规律Fig.5 Pressure change in control valve

阀芯运动速度变化工况通过控制网格模型中的阀芯部分沿轴线方向进行直线运动，以模拟阀门在不同的指令速度要求下的调节过程。起始开度40%的网格模型，设置阀芯分别以40， 60， 80， 100 mm/s的速度向上移动；起始开度100%的模型，设置阀芯以同样大小的4组速度向下移动；相对位移8 mm，在相对位移xr=3 mm处施加舰船管路突变压力，xr=4.8 mm处撤去压力。

仿真需分析阀门的附加耦合负载，包括阀芯的轴向受力、阀芯稳态压力和阀芯动态压力。其中阀芯轴向受力直观地体现阀芯的轴向负载变化情况，而稳态压力和动态压力则参与计算阀芯的液动力，其计算公式如式(1)所示：

Ff=Fs-Fd

(1)

式中，Ff—— 液动力

Fs—— 稳态压力引起的负载

Fd—— 动态压力引起的负载

其中,Fs和Fd的计算方法如式(2)、式(3)[16]所示：

(2)

(3)

式中，ps—— 稳态压力

pd—— 动态压力

Sc—— 阀芯在轴向的投影面积

在Fluent中，阀芯的稳态压力表示阀芯表面的流体静压，反映流体的压力能对阀芯的影响；而动态压力表示阀芯表面流体的动压，反映流体的动能对阀芯的影响，在仿真中，二者的大小均随着模拟舰船工况的改变而不断变化。由于选用调节阀的阀芯表面不是锥面，较难直接计算整个阀芯受的液动力。因此，选择直接对比分析其稳态与动态压力，间接分析阀芯受到的液动力的变化，从而推断附加耦合负载。

2 仿真结果与讨论

2.1 舰船压力突变工况

固定阀芯的移动速度，改变最大突变压力，模拟不同剧烈程度下的舰船管路压力突变，分别得到起始开度40%与100%的仿真结果。

1) 起始开度40%

阀芯从起始位置以40 mm/s的速度向上运动，在第0.06秒时施加突变压力，第0.1秒时撤去压力，分别导出仿真的轴向力Fa、稳态压力ps和动态压力pd，如图6～图8所示。

图6 不同突变压力下阀芯轴向力变化(起始开度40%)Fig.6 Axial force change of spool with different mutation pressures (initial opening 40%)

图7 不同突变压力下阀芯稳态压力变化(起始开度40%)Fig.7 Static pressure change of spool with different mutation pressures (initial opening 40%)

图8 不同突变压力下阀芯动态压力变化(起始开度40%)Fig.8 Dynamic pressure change of spool with different mutation pressures (initial opening 40%)

由图6可知，pmax为5 MPa时的曲线没有明显的尖峰和波动，其他3种情况下的曲线作放大处理可以看出，突变压力施加后，调节阀的阀芯受力在0.005 s内迅速上升并出现峰值，最大受力接近22 kN，上升时间随pmax的增大而减小；在突变压力即将撤去前， 阀芯受力上升约0.2 kN。由图7得，在突变压力施加时，稳态压力最大值约为pmax的60%，经过最大值后，pmax越大，稳态压力下降斜率越大；突变压力撤去时，出现了负压， 在0.02 s内恢复到正常压力值。 图8可知， 阀芯所受的动态压力最大值出现在突变压力即将撤去前，仿真过程的最大动态压力接近7.5 MPa。结合图7与图8分析，突变压力施加的时间段之外，阀芯的稳态压力大于0.5 MPa，而动态压力小于0.5 MPa，说明在这段时间内稳态压力对阀芯附加耦合负载的影响较大；pmax为5 MPa时，稳、动态压力差约为0.1 MPa，pmax为21 MPa时，稳、动态压力差约为-0.7 MPa，说明随着阀门内部突变压力的升高，动态压力对阀芯负载的影响逐渐起到主导作用。

阀芯周围的流场压力及速度云图，如图9、图10所示。由图9a可得，在突变压力(pmax=13 MPa)施加时，阀芯下部压力接近13 MPa，阀芯上部压力约为2 MPa，且在阀芯的上部边缘处出现负压区。由图10a得，pmax为21 MPa时阀芯周围负压区的面积扩大。对比图9b和图10b，pmax为13 MPa的突变压力施加时，最大流速达到140 m/s，pmax为21 MPa时，最大流速达到170 m/s；当突变压力撤去后，二者阀芯周围最大速度为约58 m/s；阀芯左侧存在有2个旋涡，阀芯左下方有1个较小的旋涡，紧贴在侧壁上，在突变压力撤去时，pmax为13 MPa时阀芯右上方有旋涡出现，而pmax为21 MPa时对应位置无旋涡生成。

图9 阀芯周围流场情况(pmax=13 MPa，起始开度100%)Fig.9 Flow field around spool (pmax =13 MPa, initial opening 40%)

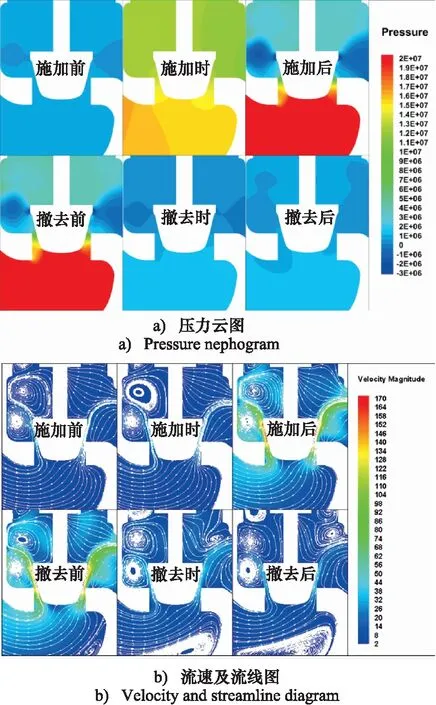
图10 阀芯周围流场情况(pmax=21 MPa，起始开度100%)Fig.10 Flow field around spool (pmax =21 MPa， initial opening 40%)

2) 起始开度100%

起始开度100%时调节阀模型的轴向力与压力随时间的变化规律，如图11～图13所示。

由图11得，当突变压力为21 MPa时轴向力最大，为11 kN。在压力突变段内，4条曲线的压力增加率均高于其他时间段。图11b局部放大图得，在压力突变时，当pmax分别为13，17， 21 MPa时的3条曲线在经过0.003 s后达到一个峰值，随后呈波动上升趋势。如图12所示，阀芯所受稳态压力在入口压力发生突变时出现明显的尖峰， 后迅速下降，达到相对稳定的压力，每条曲线的稳定压力值接近pmax的30%，而峰值大小约为pmax的60%。当入口压力突然减小到正常压力值时，阀芯出现了负压。图13显示阀芯所受动态压力最大值出现在pmax为21 MPa条件下，约为8.8 MPa。峰值之后稳定在最大突变压力的40%左右。结合图12与图13，在突变压力施加时，稳态动态压力差随pmax的增加而增大，pmax为21 MPa时，达到-2.5 MPa左右。

图12 不同突变压力下阀芯稳态压力变化(起始开度100%)Fig.12 Static pressure change of spool with different mutation pressures (initial opening 100%)

图13 不同突变压力下阀芯动态压力变化(起始开度100%)Fig.13 Dynamic pressure change of spool with different mutation pressures (initial opening 100%)

起始开度100%，pmax分别为13，21 MPa时阀芯周围流速及流线图，如图14、图15所示。pmax为13 MPa时，最大流速达到140 m/s；pmax为21 MPa的突变压力施加时，最大流速达到178 m/s。从流线观察，pmax为13 MPa时，突变压力施加后瞬间，其在阀芯右上方出现了1个较小的旋涡；pmax为21 MPa时，在此位置没有明显的旋涡生成。而在突变压力撤去时，两图的阀芯右上方的出现旋涡，当流场相对稳定后，此旋涡移动至阀腔边缘，阀芯右下方流道内部的旋涡也随之出现。

图14 阀芯周围流速及流线图(pmax=13 MPa，起始开度100%)Fig.14 Velocity and streamline around spool (pmax=13 MPa, initial opening 100%)

图15 阀芯周围流速及流线图(pmax=21 MPa，起始开度100%)Fig.15 Velocity and streamline around spool (pmax=21 MPa, initial opening 100%)

2.2 阀芯速度变化工况

固定舰船的管路突变压力，改变舰船调节阀阀芯移动速度，分别得到起始开度40%与100%的仿真结果。

1) 起始开度40%

阀芯从起始位置分别以40，60，80，100 mm/s的速度向上运动，在相对位移xr为3 mm处施加舰船管路13 MPa突变压力，xr为4.8 mm处撤去压力，得到阀芯轴向受力、稳态压力和动态压力，如图16～图18所示。

由图16a可得，阀芯所受轴向力在突变压力施加的时间段内呈现波动下降；最大轴向力约12.18 kN，此时阀芯速度40 mm/s，轴向力的峰值随阀芯速度的增加而减小，各移动速度下的阀芯受力均呈现较为明显的波动。其中阀芯速度60 mm/s时受力在峰值之后是最小的。如图16b所示， 峰值时间最短为阀芯速度100 mm/s时，约为0.0047 s。阀芯移动速度增加，其轴向力波动的频率逐渐增加。

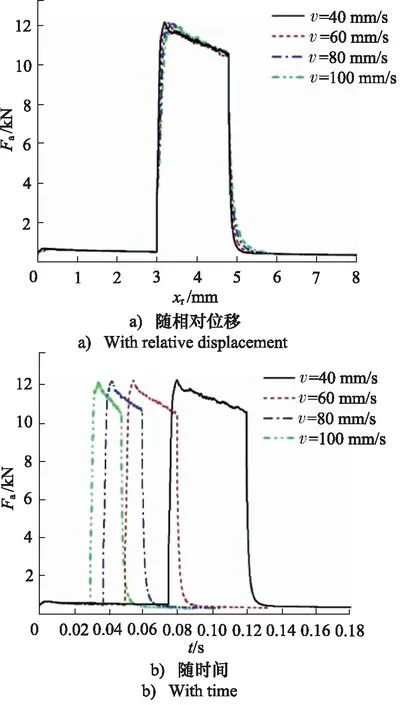
图16 不同阀芯速度下阀芯轴向力变化曲线(起始开度40%)Fig.16 Axial force change of spool with different speeds (initial opening 40%)

由图17得，经过峰值后，阀芯的稳态压力沿斜率较小的直线下降，4条曲线在此段几乎重合。图18可知，阀芯所受的动态压力在突变压力施加时迅速上升并出现波动，最大值出现在阀芯速度为40 mm/s时，约为4.8 MPa。结合图17与图18，在突变压力施加时，静、动态压力差达到-0.6 MPa。图16～图18说明，随着突变压力施加，阀芯受到的附加耦合负载随着阀芯的移动而不断波动，阀芯的运动速度越大，附加耦合负载的波动频率越大，阀芯受力就越不稳定。

图17 不同阀芯速度下阀芯稳态压力变化(起始开度40%)Fig.17 Static pressure change of spool with different speeds (initial opening 40%)

图18 不同阀芯速度下阀芯动态压力变化(起始开度40%)Fig.18 Dynamic pressure change of spool with different speeds (initial opening 40%)

2) 起始开度100%

阀芯从起始位置分别以v为40，60，80，100 mm/s的速度向下运动。

从图19a可得，阀芯所受轴向力在突变压力施加的时间段内呈现波动上升；突变压力施加时，调节阀的阀芯受力出现峰值，约5480 N，此时阀芯速度100 mm/s；仿真过程的最大值出现在速度60 mm/s突变压力即将撤去时，为6900 N。阀芯受力的峰值时间如图19b所示，每条曲线的峰值时间均接近0.005 s。

图19 不同阀芯速度下阀芯轴向力变化(起始开度100%) Fig.19 Axial force change of spool with different speeds (initial opening 100%)

由图20得，在突变压力施加时，阀芯所受稳态压力出现明显的尖峰，约为pmax的60%。经过峰值后，稳态压力稳定在3.8 MPa左右。突变压力撤去时出现了负压，约为-3.4 MPa。由图21可知，阀芯所受的动态压力最大值出现在阀芯速度80 mm/s时，约为5.3 MPa。结合图20与图21，突变压力施加时，静、动态压力差达到-1.6 MPa左右，说明阀芯运动速度的大小对压力差的影响很小。

图20 不同阀芯速度下阀芯稳态压力变化(起始开度100%)Fig.20 Static pressure change of spool with different speeds (initial opening 100%)

图21 不同阀芯速度下阀芯动态压力变化(起始开度100%)Fig.21 Dynamic pressure change of spool with different speeds (initial opening 100%)

3 结论

(1) 舰船管路内的压力和调节阀阀芯的移动速度产生较大改变时， 调节阀受到的附加耦合负载也会产生相应变化。阀芯从下向上移动调节时，其附加耦合负载逐渐减小；阀芯从上向下移动，附加耦合负载逐渐增大。流体输入调节阀的压力变化对附加耦合负载的影响较大，而阀芯本身在调节过程中，因为阀芯的移动而受到的附加耦合负载变化较小；

(2) 随着舰船管路压力的增大，阀芯受到动态压力逐渐超过稳态压力，附加耦合负载随着动态压力而不断波动。同时阀芯的运动速度越大，轴向受力波动频率越大。阀芯仿真过程中，阀芯受到的最大轴向受力已经超过20 kN，受到的最大稳态压力接近13 MPa，若此受力超过执行机构的最大输出力，调节阀将失去调节能力，影响舰船航行安全；

(3) 附加耦合负载会使阀门内部产生负压，阀腔内部的流体在阀芯周围出现空化现象，随着附加耦合负载的增大，负压区增大。不仅会影响调节阀的调节，而且会造成阀芯损伤，缩短调节阀相关零部件的使用寿命。在这种情况下，以上结果可对舰船调节阀的控制及设计进行参考，下一步可对附加耦合负载的补偿方法进行探讨。