有限时间不确定性估计的电液伺服跟踪控制技术
李 帅, 郭 庆, 蒋 丹
(1.电子科技大学 航空航天学院, 四川 成都 611731; 2.电子科技大学 机械与电气工程学院, 四川 成都 611731)
引言
作为一类典型的机电系统,电液伺服系统凭借其超大的能量密度以及超高的调节精度,被广泛应用于工业工程应用中,如风力机、机器人以及热压成型机等[1-3]。作为电液伺服系统研究的一个重要方向,控制算法的研究一直以来都备受学者们的关注, 多种控制器的设计方法都被应用到了电液伺服系统中,比如滑模控制器[4]、神经网络控制器[5]和鲁棒积分控制器[6]等。但这几类控制器都有着十分明显的优缺点:滑模控制器的构造方式更为简单并且相应性能更加出色, 但在控制过程中极易出现振颤现象,进而影响控制效果;神经网络控制器具备很好的鲁棒性以及学习能力,但容易陷入局部最优解中;鲁棒积分控制器在稳态区间内具有极佳的控制性能,但在瞬态区间内的控制效果欠佳。本研究采用了反步控制方法来对电液伺服系统进行控制器设计。相较于之前列举的几类控制器,反步控制器的鲁棒性优秀,全局求解能力卓越并且在瞬态和稳态都有不错的控制能力。虽然反步控制器的设计步骤较为复杂,但鉴于可参考的成果较多[7-9],可为本研究的研究提供足够的帮助。
除了控制器的设计之外,由于参数不确定性的存在,如何对电液伺服系统的这类扰动进行补偿就成为十分迫切的问题。事实上,很多种观测器已经应用于电液伺服系统的控制当中,比如自适应观测器[10-11]、高增益观测器[12]以及扩展状态观测器[13]等。自适应观测器凭借其较简单的结构,广泛应用于对系统全状态的估计当中。高增益观测器具有更好的控制精度,但同时所需的控制带宽也更大;扩展状态观测器可以在模型信息未知的前提下对系统的状态和模型进行估计。通过以上介绍可知,参数不确定性的估计精度已经得到极大的提高,但另一方面,参数不确定性估计速度一直没有被重视,是一个可以研究的发展方向。
作为一种可以对参数不确定性进行快速估计的观测器,终端滑模观测器自2009年问世以来便得到了大量学者们的关注,并广泛应用于各类机电系统中,比如永磁同步电机[14]、Buck变换器[15]、风力机组[16]等,这类观测器对不确定性的估计速度更快,进而使得被研究系统的输出响应效果更好。事实上在现阶段的电液伺服系统控制研究中,各类观测器对系统参数不确定性的估计精度已经达到了十分理想的水平,基于此,如何更加快速地估计参数不确定性成为了一个十分有意义的研究方向。
本研究的主要贡献是将反步控制器的控制方法同终端滑模观测器的设计相结合,得到了一种新的电液伺服控制系统的控制算法,通过工程平台的实验验证,结果表明,新的控制算法确实能够得到更好的控制效果,使得电液伺服系统的输出响应结果更加出色。
1 电液伺服系统数学建模
电液伺服系统一般包括泵站、伺服阀、液压缸以及负载对象,如图1所示[17-18]。
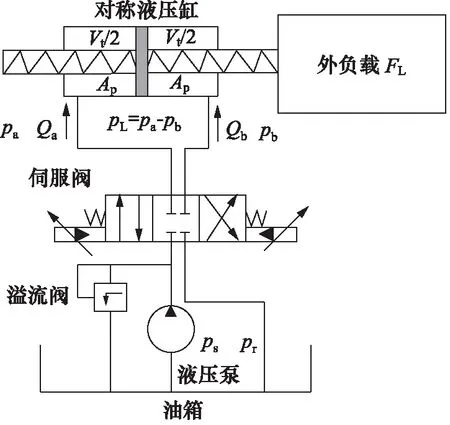
图1 电液伺服系统示意图Fig.1 Diagram of electrohydraulic servo systems
(1)
式中,
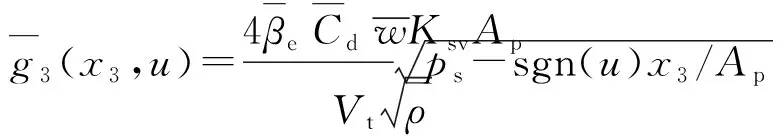
(2)
sgn函数定义为:
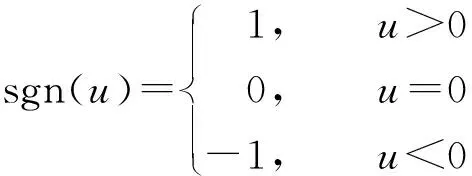
(3)
假设1:两个集总不确定性Δ2和Δ3是有界的,满足|Δi|≤Di,i∈{2,3},其中Di为已知的正常数。
2 终端滑模观测器设计
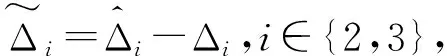
定义终端滑模面为:
(4)
其中,辅助变量v2和v3被定义为:
(5)
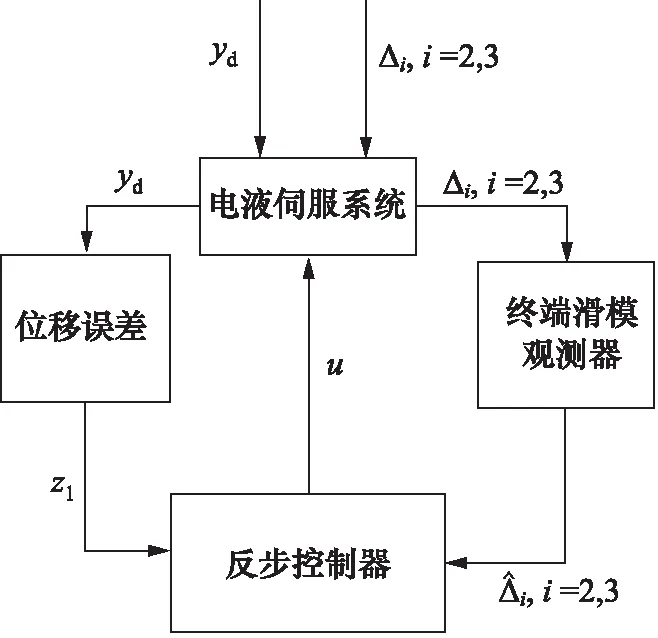
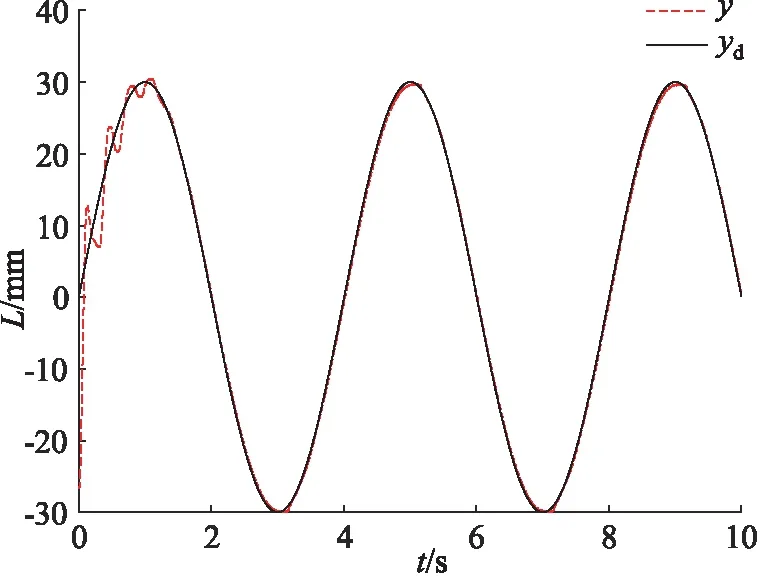
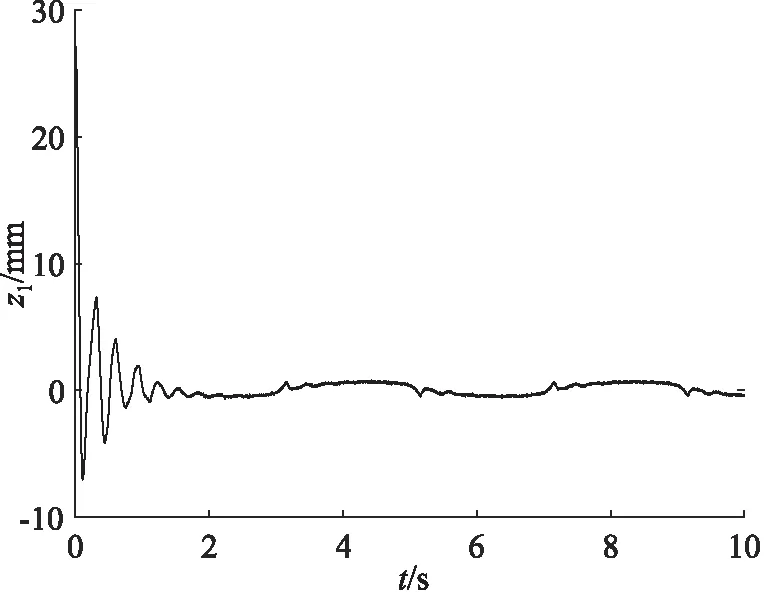
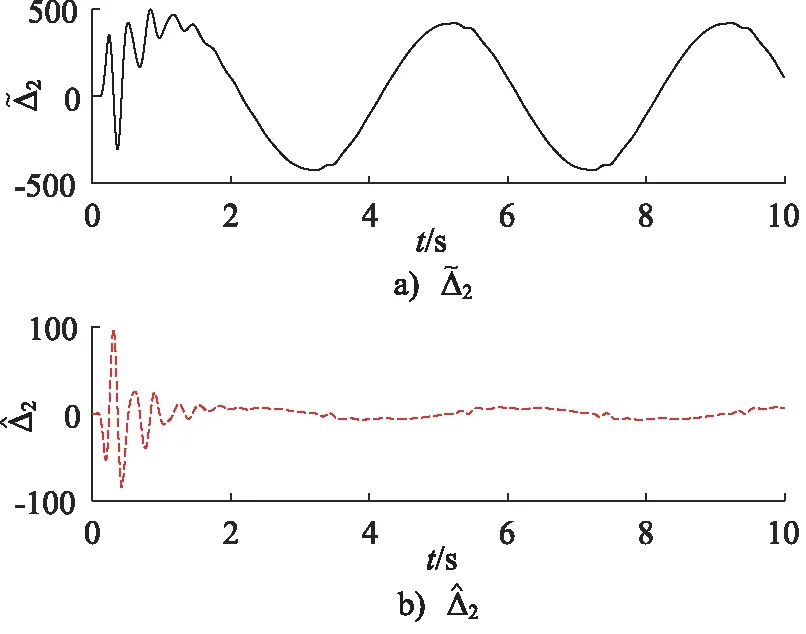
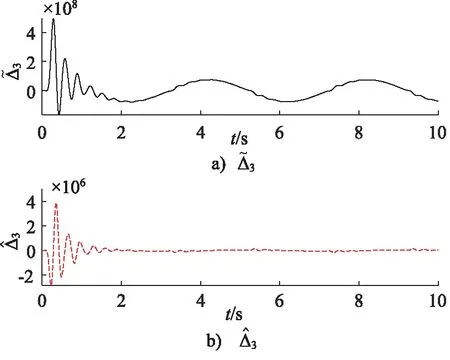
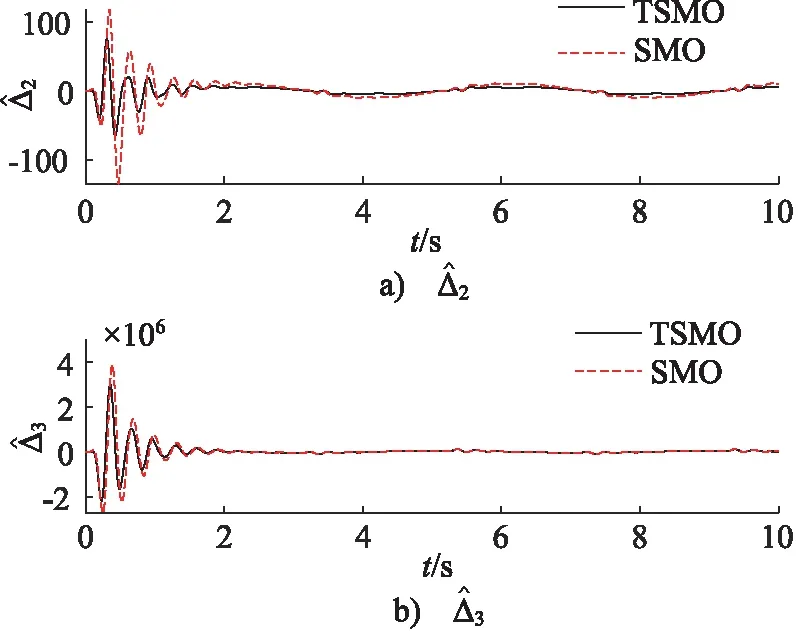
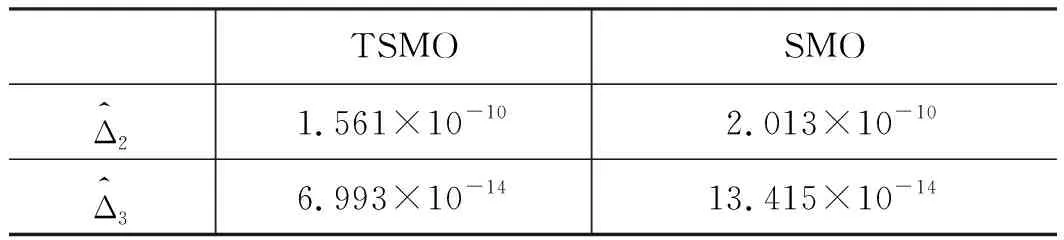
式中,kdi,di和εi为正常数,pi和qi均为正奇数,且pi 那么终端滑模观测器估计值表示为: (6) 引理1[19]:如果存在一个正定的李亚普夫函数V(t) 满足: (7) 式中,a,b>0,0 (8) 证明:针对集总式不确定项Δ2,选择李雅普诺夫函数如下: (9) 则Vs2的导数为: |s2||Δ2| (10) 基于假设1,进而得出: (11) 而估计误差为: (12) 同理,针对集总式不确定项Δ3,选择李雅普诺夫函数如下: (13) 则Vs3的导数为: |s3||Δ3| (14) 又基于假设1,可进而得出: (15) 而估计误差为: (16) 此部分将会提出一个基于终端滑模观测器的反步控制器的设计算法,首先,给定一组误差方程如下: (17) 并将此误差方程进行求导,得出: (18) 为了实现电液伺服系统的位移跟踪控制,2个虚拟控制变量α1,α2以及1个控制输入u将被定义为: (19) 式中,k1,k2和k3是3个可调节的控制增益,均是大于0的常数。 定理2:对于电液伺服系统式(1),若考虑终端滑模观测器式(4)~式(6)以及递归反步控制器式(17),那么,此系统将会渐进跟踪期望轨迹yd,从而实现了所需的控制效果。 证明:首先,构造李雅普诺夫函数如下: (20) 并根据此李雅普诺夫函数构造一系列的级联项如下: (21) 由于控制器是基于反步法进行设计的,所以本研究将会把接下来的稳定性证明分为3个步骤进行分析。 第一步:结合式(17)~式(19),可以得出: (22) 第二步:根据式(12)、式(17)~式(19)、式(22),可以得出: (23) 第三步:根据式(16)、式(19)、式(23),可以得出: ≤0 (24) 由于V3=V,所以不等式(24)也说明状态变量x1,x2,x3将会渐进地收敛到平衡点,这也说明了本研究所设计的控制器实现了电液伺服系统的渐进追踪控制。 证明完毕。 本研究所提出的控制策略的流程图如图2所示。 图2 控制流程图Fig.2 Control flow diagram 为了验证本研究所提出的控制策略,搭建了一个实验平台,组成部分如下:泵站(HY-36CC-01/11 kW),喷嘴挡板伺服阀(D633-R04K01M0NSM2),液压缸(UG1511R25/16-100),如图3所示。 图3 电液伺服系统实验平台Fig.3 Experimental platform of electro-hydraulic servo systems 在实验过程中,液压缸的位移数据通过位移转换器(BD-sensors-DMP-331)进行传输,并且同液压缸负载压力一起被NI卡(PCI-6237/21 DA1)进行采集。基于采集的数据,本研究所提出的控制算法便可以由上位机的MATLAB软件进行构造,并通过NI卡传递至伺服阀,进而实现控制目的。由于考虑了气缸位置的机械约束和伺服阀的控制饱和,本研究设定期望轨迹是一个频率和幅度都不高的正弦曲线。 由于所提出的控制算法是针对单个电液伺服系统的控制算法,所以图3中只有一个执行器被控制。为了说明结论的可行性,本研究设计终端滑模观测器参数kd2=66,kd3=1.5,D2=2,D3=2,ε2=88,ε3=3,以及分数项p2/q2=p3/q3=5/7,并给定控制器参数k1=370,k2=300,k3=600。基于以上参数,电液伺服系统实验平台可实现追踪控制。 图4展示了实验当中的实际位移y与期望轨迹yd。经过前期的一段振颤后,实际位移y逐渐趋近于期望轨迹yd。两条轨迹的误差如图5所示,经过前期的一段振颤后,实际位移y与期望轨迹yd的位移误差收敛于0。 图4 实验中的实际位移与期望位移Fig.4 Actual and expected positions in experiment 图5 实际位移与期望位移间的位移误差Fig.5 Position error between actual and expected position 图6和图7分别为参数不确定性项Δ2和Δ3的估计值与估计误差,经过前期的一段振颤后,估计误差逐渐收敛到0。图8为终端滑模观测器(TSMO)与常规滑模观测器(SMO)的估计误差数据。终端滑模观测器的估计误差在前期振颤阶段相较于常规滑模观测器具备更小的振幅,体现出了终端滑模观测器的优越性。表1对2种观测器的估计误差进行了量化,对比表中数据,依然可得出终端滑模观测器具备更好的扰动估计性能的结论。 图6 Δ2的估计值及估计误差Fig.6 Estimation value and estimation error of Δ2 图7 Δ3的估计值及估计误差Fig.7 Estimation value and estimation error of Δ3 图8 终端滑模观测器与滑模观测器对比Fig.8 Contrast between TSMO and SMO 表1 终端滑模观测器与滑模观测器的估计误差Tab.1 Estimation errors of TSMO and SMO 图9为实验中的控制输入电压,由于本研究给定的期望轨迹是正弦信号,所以控制输入也近似于正弦波。 图9 实验中的控制输入Fig.9 Control input in experiment 本研究提出了一种全新的电液伺服控制算法。首先,为电液伺服系统设计了终端滑模观测器,对电液伺服系统所存在的参数不确定性进行估计和补偿;在此基础上,本研究设计并提出了反步控制算法,来实现电液伺服系统的跟踪控制;最后,通过平台实验,验证了算法的可行性。通过以上的研究发现,终端滑模观测器相较于常规的滑模观测器,可以对电液伺服系统的参数不确定性进行更为快速地估计,进而提升电液伺服系统的跟踪控制性能。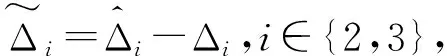
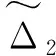
3 反步控制器设计
4 实验验证


5 结论

