中空玻璃板单向冷弯力学行为试验及数值研究

张喜德 梁金志 江佳霖

(1.广西大学 土木建筑工程学院，广西 南宁 530004；2.工程防灾与结构安全教育部重点实验室，广西 南宁 530004；3.广西工程防灾与结构安全重点实验室，广西 南宁 530004)

近年来，越来越多的建筑物使用曲面玻璃来制作现代建筑的外墙[1- 2]。曲面玻璃分为热弯玻璃和冷弯玻璃，热弯玻璃是通过热弯成型法实现，而冷弯玻璃则是通过冷弯成型法实现。使用传统的热弯成型法来制作曲面玻璃，造价高、周期长，且易引起光学质量缺陷[3- 5]。冷弯成型法则可以较好地避免光学缺陷等问题[6]，其利用玻璃具备一定弹性变形能力的特点，在工地常温下将玻璃板弯曲就位。此外，冷弯玻璃还可以在工厂批量预制[7]，施工效率可大大提升。该技术自2002年首次应用[8]，至今已在许多项目中得到应用[9- 15]。

对于这一充满前景的玻璃幕墙弯曲成型方法，相关研究较为滞后和有限，并且近年来对于冷弯玻璃的研究对象多数集中在单片玻璃和夹层玻璃上[3，8，16- 21]，并且有一种趋势是利用实验来研究冷弯，如Spagnoli等[8]和Quaglini等[22]的研究。为满足节能要求，大多数国家、地区对建筑围护结构采用的做法是安装中空玻璃组件[23]，在中国已有相关标准要求在寒冷地区必须采用中空玻璃[24]，目前中空玻璃组件的大多数研究都集中在热、耐久性和隔音等方面[25]，有关曲面中空玻璃幕墙采用冷弯成型法的研究成果还不多，未能满足实际工程应用的需求，这在很大程度上限制了冷弯成型法的发展。

冷弯中空玻璃的应力和变形难以计算，主要是密封胶的作用复杂[26]，对冷弯成型后边缘区组件结构内部的应力产生影响。在冷弯后再与各种荷载耦合作用可能使玻璃结构处于更不利的受力状态，甚至导致幕墙玻璃面板脱落。

本文对中空玻璃的单向冷弯力学行为进行试验研究，侧重于分析使用冷弯成型法的中空玻璃的不同影响因素，包括玻璃板厚度、空腔厚度以及冷弯曲率对应力分布以及玻璃面板的相对滑移的影响，以便为工程设计提供参考。

1 试验概况

1.1 试件设计

根据正交试验设计原理，共制作了9个试件进行冷弯加载试验，具体试件参数见表1。表中，t为玻璃厚度，tc为空腔厚度，ρ为冷弯曲率。每一块中空玻璃都采用1 200 mm×600 mm的尺寸。试验中的间隔条以及密封胶均满足中国规范JGJ102—2003[27]的要求，中空玻璃的间隔条通常要求质地较硬，因而采用铝隔条以确保中空玻璃板的力学整体性，通过改变铝隔条的厚度来得到所需的空腔厚度；按中国规范要求，密封胶有两道，分别采用硅酮胶和丁基胶。

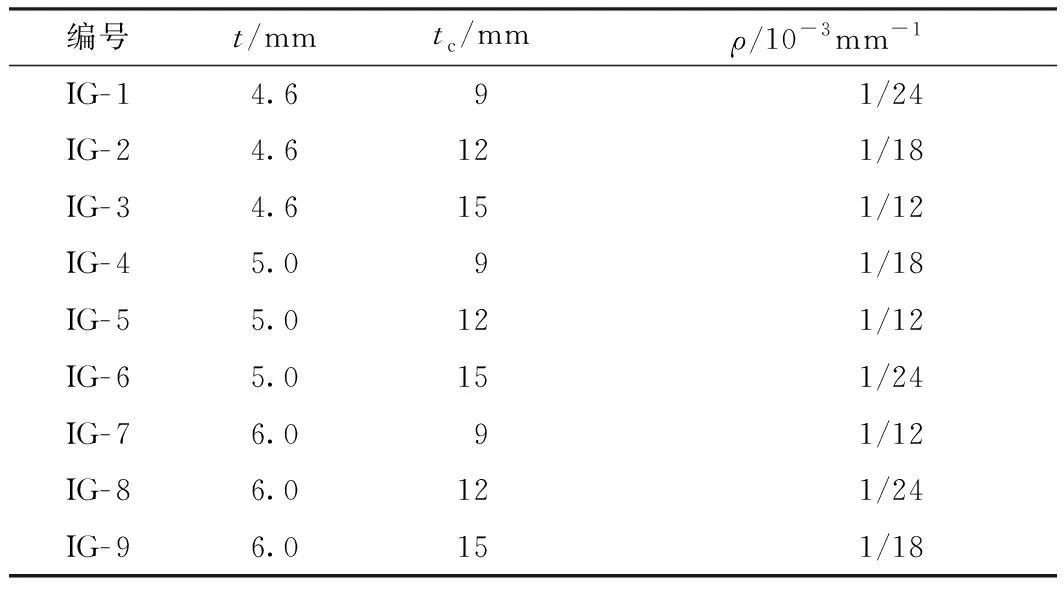
表1 试件参数Table 1 Test parameters

正交试验要求各影响因素取不同的值，称为水平，这里的影响因素为冷弯曲率、玻璃板厚度以及空腔厚度，分别取3个不同的值。玻璃板的厚度(t)参考常用的厚度分别采用4.6、5.0和6.0 mm；空腔厚度(tc)不能过小，JGJ102—2003规范[27]要求空腔厚度在9 mm以上，试件的空腔厚度采用9、12和15 mm；考虑冷弯曲率(ρ)的影响时，在冷弯范围内选取1/12 000、1/18 000和1/24 000 mm-1。试件的中空玻璃各大面的命名规则如图1所示。用“A”、“B”分别表示上、下片玻璃；用“1”、“2”分别表示玻璃的上、下表面。

图1 中空玻璃面的构造Fig.1 Structure of insulating glass plate

1.2 试验装置与试验方法

根据实际冷弯施工技术和特点对试验加载装置进行设计，如图2所示。试验装置主要由曲边支承梁、钢横梁和支承底座组成。其中曲边支承梁采用硬质木材精确加工制成，如图3所示。其作用是为中空玻璃提供支承以及形成圆弧边界形态，当玻璃贴合曲边梁时，玻璃即达到所需的冷弯曲率。

图2 冷弯试验装置Fig.2 Cold bending test device

图3 曲线支承梁Fig.3 Curved support beams

试件放置在曲边支承梁上，在曲边支承梁一端用两个夹具将试件固定，夹具与玻璃板之间加一块橡胶垫，如图4所示。而另一端则通过施加重物使其产生位移，为了方便加载，重物采用铅块并进行分级加载，如图2、图5所示。每级荷载采用两块铅块分别对称分布在玻璃加载端上，每级施加的荷载为96 N。由于玻璃在受力时表现出微小滞弹性，这个滞弹性约为初期弹性应变的10%[28- 29]，考虑到玻璃的此种特性，同时为使间隔材料的变形稳定，在每级冷弯位移完成后保持15 min，然后采集数据。整个冷弯过程中，均保持温度为(25±1) ℃。

图4 固定夹具Fig.4 Fixtures of specimen

图5 冷弯加载Fig.5 Cold bending load

1.3 量测方案及加载方法

应变测点布置如图6所示，冷弯加载区的应变不易测量，同时单向冷弯的试件的应变通常具有轴对称性，因而在上表面(A- 1及B- 1面)和下表面(A- 2及B- 2面)的固定端一侧的1/4面分别布置18个和12个应变测点，同时在玻璃的剩下的3个角点各布置1个对称性校准的应变测点来验证上述的对称性。

(a)A- 1测点(括号内)和B- 1测点(括号外)

(b)A- 2测点(括号内)和B- 2测点(括号外)图6 应变测点(单位：mm)Fig.6 Strain measuring points(Unit：mm)

中空玻璃的内表面测点的应变计需要在玻璃板合片制作前粘贴完成，然后在工厂按照加工流程安装铝隔条以及封装密封胶，应变计的导线通过在铝制隔条上的预留孔洞引出。在图5中可看到引出的导线，所有应变计均采用由3个应变片构成的直角形应变花。

除测量应变以外，试验过程中还监测了位移，在玻璃面板上的9个位移测点上用百分表测量其竖向位移；另外在固定端上下两片玻璃板外边缘分别布置位移测点S10、S11，采用千分表测量上下两片玻璃板的层间位移。具体测点布置如图7所示。

图7 位移测点(单位：mm)Fig.7 Displacement measuring points(Unit：mm)

2 试验结果与分析

2.1 板面主应力分布

根据应变采集系统采集到的数据，可以获得各个测点的第1主应力σ1与第2主应力σ2，通过各测点的主应力来分析不同玻璃面板的主应力分布。试验结果如下：

(1)表2列举了IG- 1、IG- 5、IG- 9这3个试件在A片玻璃上两个面的校准点对应的主应力数值，表中第1行的数字是测点号，括号内外的数字分别是A- 2面和A- 1面上的校准测点号，详见图6。从总体上来看，4个对称性的应变校准点数据与测量角点的应变数值的偏差在9.33%以内，这说明单向冷弯的中空玻璃的在试验过程中具有良好的中心对称性。

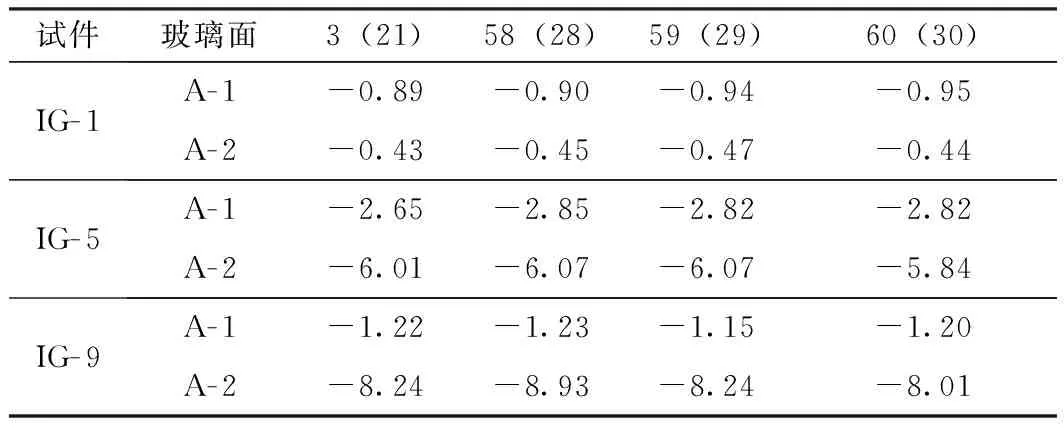
表2 校准点主应力值Table 2 Principal stress values of calibration points MPa

(2)不同试件各个面的主应力极值有着类似的规律，IG- 1、IG- 5、IG- 9在实验中各个面出现的主应力极值见表3。从表中可以看出，玻璃面板的最大主应力出现在A- 1面，该面主应力极值比其他几个面的都大，并且差距十分明显，破坏应力可能产生于A- 1面。表3中的A- 2面、B- 1面的最大主应力σ1，max只有A- 1面的50%～60%；B- 2面主应力极值则更小，不到A- 1面的40%，说明在冷弯过程中，由于间隔条的存在，使得冷弯作用在传递过程中发生了一定下降。

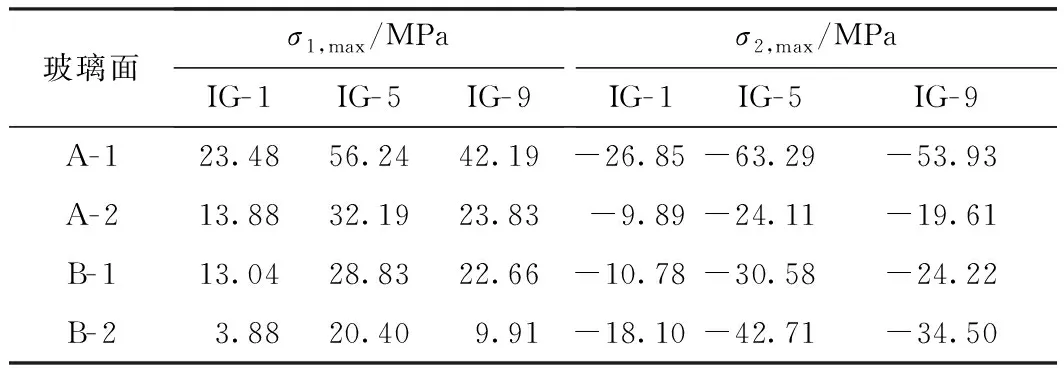
表3 各面的最大主应力Table 3 Maximum principal stress of each surface

(3)根据各测点的试验数据，利用MATLAB软件按照中心对称性绘制各个试件的主应力云图。各个试件的分布规律类似，这里以IG- 1为例说明。图8(a)-8(d)分别为试件IG- 1在A- 1、A- 2、B- 1、B- 2面上的主应力σmax，Abs的应力云图，σmax，Abs为绝对值最大的主应力。从整体上看，中空玻璃的冷弯主应力分布极不均匀，玻璃的边缘局部产生极值应力，在长边的1/2至1/4处的主应力等值线分布较为密集。在A- 1面中，主应力等值线较为密集的部位有两处，第1处为长边中点附近；第2处为夹具与玻璃表面接触处。B- 2面的主应力以压应力为主。

主应力极值出现在边缘，原因与板的变形密切相关。变形主要源于两端的约束和冷弯荷载。在中空玻璃冷弯就位后，两端的约束对玻璃的作用最大，但玻璃中部的弯曲曲率最大，此外，玻璃的A- 1面没有间隔条的约束，主应力极值点位于板边缘中点，如图8(a)所示。而位于空腔内表面的A- 2面和B- 1面的主应力分布有较明显的不同。由于间隔条的约束作用，主应力极值不在长边中点处，有两个极值点，分别位于长边中点的两侧。

(a)A- 1

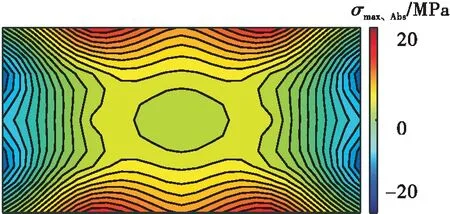
(b)A- 2

(c)B- 1

(d)B- 2图8 IG- 1主应力云图Fig.8 Principal stress nephograms of IG- 1

2.1.1 冷弯曲率的影响

根据正交试验分析原理，可分析各因素对主应力的影响。对冷弯曲率进行分析时，玻璃厚度及空腔厚度的指标均值分别为5.2 mm及12.0 mm，冷弯曲率的变化对中空玻璃各个面的主应力影响见表4-5，表中σ1，max、σ2，max分别为第1、2主应力的最大值。

表4 曲率对A片玻璃最大主应力的影响Table 4 Influence of curvature on maximum principal stress of A-piece glass

表5 曲率对B片玻璃最大主应力的影响Table 5 Influence of curvature on maximum principal stress of B-piece glass

从表4-5中可以看出，冷弯曲率的增大会使冷弯主应力有显著的增长。冷弯曲率的增大意味着中空玻璃的弯曲变形的增大，同时所需的作用在玻璃端部的冷弯荷载会增大，玻璃中部受到的弯矩也会增大。因此冷弯曲率越大的试件，其冷弯主应力也就越大。在同一冷弯条件下，冷弯曲率从1/24 000 mm-1增加到1/12 000 mm-1时，A面最大主应力值σ1，max增加了108%左右。

2.1.2 空腔厚度的影响

空腔厚度的变化对中空玻璃各个面的主应力极值影响见表6-7，冷弯曲率及玻璃厚度的指标均值分别为1/16 666 mm-1和5.2 mm。从表6-7中可以看出，随着空腔厚度的增大，主应力也随之增大，但增幅不大：在同一冷弯条件下，空腔厚度从9 mm变化到15 mm，最大主应力增幅在10%～32%之间。

表6 空腔厚度对A片玻璃最大主应力的影响Table 6 Influence of cavity thickness on the maximum principal stress of A-piece glass

表7 空腔厚度对B片玻璃最大主应力的影响Table 7 Influence of cavity thickness on the maximum principal stress of B-piece glass

对中空玻璃而言，空腔厚度的增大将会使玻璃板的整体刚度有所增大，因此其弯曲应力将会有所增加。此外，空腔厚度越大的中空玻璃，由于冷弯后空腔气体压缩的体积也越大，因此玻璃内部受到的压力将会增高，并加剧板的变形。空腔厚度变化不大时，对玻璃板主应力的影响有限，而由于间隔条强度比玻璃的小得多，空腔厚度的增加对边缘区域的刚度影响不大，当间隔条厚度增大，其纵向弯曲刚度的变化很小[30]。因此，冷弯主应力增幅不大。

2.1.3 玻璃厚度的影响

玻璃厚度的变化对中空玻璃各个面的主应力影响变化如表8-9所示，冷弯曲率及空腔厚度的指标均值分别为1/16 666 mm-1和12 mm。从表中可以看出，玻璃厚度从4.6 mm变化到6.0 mm，主应力极值增幅仅在3%～12%之间。

表8 玻璃厚度对A片玻璃最大主应力的影响Table 8 Influence of glass thickness on maximum principal stress of A-piece glass

表9 玻璃厚度对B片玻璃最大主应力的影响Table 9 Influence of glass thickness on maximum principal stress of B-piece glass

从表8-9中可以看出，玻璃板厚的变化对于主应力的影响较弱。玻璃板厚度增加后，中空玻璃板的整体厚度和刚度有所增大，这与空腔厚度的影响相似。然而由于空腔内的压力基本相同且玻璃厚度变化较小，对玻璃板的弯曲应力影响有限，因此其应力增幅较小。

2.1.4 极差分析

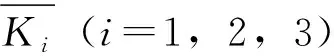
表10 A- 1面各因素的最大主应力极差Table 10 Maximum principal stress ranges of different factors on the surface A- 1

从表中可以看出，冷弯曲率对应的极差为29.77，为三者中最大，说明其对冷弯过程中主应力的影响最大，其次为空腔厚度和玻璃厚度，两者的极差较小且十分接近，这也说明了空腔厚度和玻璃厚度的增大对玻璃板面主应力的影响程度相近。

2.2 层间位移

中空玻璃冷弯变形会使上下玻璃有所错动而引起层间相对滑移u，如图9所示，冷弯试验后中空玻璃的层间剪切角θ可以用下式计算：

θ=arctan(u/tc)

(1)

图9 层间剪切角Fig.9 Inter-laminar shear angle

可根据安装于固定端面的千分表读数计算出各个试件的层间位移及剪切角，见表11。根据试验数据利用极差分析方法分析各个因素对冷弯层间剪切角θ的影响，结果详见表12。表中，θt表示玻璃板厚度影响下的剪切角，θtc表示空腔厚度影响下的剪切角，θρ表示曲率影响下的剪切角。

表11 层间相对位移及剪切角Table 11 Inter-laminar relative drifts and shear angles

假设两片钢化玻璃全部都达到所预定的曲率，且空腔厚度保持不变，可以通过几何关系式θ=Lρ/2 近似计算出层间剪切角，其中L为矩形玻璃板长边的边长，经计算发现，试验的剪切角比计算的小，如t=4.6 mm，tc=15 mm，ρ=1/12 000 mm-1的中空玻璃，试验得出的层间剪切角为2.12°，而根据假设计算的为2.86°。这是由于冷弯过程中A片玻璃没有受到模具约束，其实现的曲率要小于B片玻璃。

从表11-12可以看出：①所有试验的层间剪切角都不大，不超过2.7°；②玻璃厚度、空腔厚度以及冷弯曲率的增加，都分别对层间剪切角有增大的影响，其中冷弯曲率对应的剪切角极差达1.21，为各因素中最大，而空腔厚度和玻璃厚度对应的剪切角极差十分小。这说明层间位移主要受冷弯位移的影响，空腔厚度以及玻璃厚度的影响较小。

表12 不同因素间的剪切角的极差Table 12 Ranges of the shear angle of different factors

3 有限元分析

3.1 材料属性

在有限元的建模中，材料属性参数见表13-14。表中，C10、C01为材料常数，D为材料的不可压缩参数，C1、C2、C3为与温度有关的材料参数[31]。其中，玻璃、铝隔条材料属性取自中国规范JGJ102—2003[27]。硅酮胶的本构选用Yeoh模型，其计算结果与大变形的试验数据吻合较好[31]。橡胶垫的本构关系选用Mooney-Rivlin模型。此外，丁基胶的参数设置参考Pölzl[32]和Hagl[30]的研究，并采用绑定约束方式简化。

表13 弹性材料参数Table 13 Properties of elastic material

表14 超弹性材料参数Table 14 Properties of hyperelastic material

图10 网格划分Fig.10 Finite element mesh

3.2 网格划分

在有限元的模拟中，对于玻璃板，网格划分尺寸为 12.5 mm，曲边梁网格划分尺寸为5.0 mm，橡胶垫片网格划分尺寸为 6.0 mm，硅酮结构密封胶网格划分尺寸为 6.0 mm，铝隔条网格划分尺寸为3.0 mm。各个组件的网格划分采用中性轴算法扫描生成。其中，玻璃和铝隔条采用S4R减缩积分的四边形shell单元结构化网格，对于不可压缩材料如橡胶垫片和有机硅酮密封胶，采用C3D8RH混合的solid单元，模型整体网格及各部件网格划分参见图10。

3.3 相互作用及荷载边界

玻璃和曲边梁以及玻璃与橡胶垫的相互作用，在ABAQUS中采用“面-面”接触的方式。此外，考虑到中空玻璃空腔内的气体传动效果，在ABAQUS中设置为“流体腔”的相互作用进行模拟，空腔压力与外界压力相同，设置为 0.101 MPa，理想气体常数值取8.314 J/(mol·K)。设置一个具有圆弧接触面的柔性加载器，从而减小应力集中。

对于荷载边界条件，加载历程通过设置不同的分析步来模拟，考虑到玻璃受到的重力作用，在初始分析步后设置一个重力荷载的分析步，并在整个玻璃模型上施加自重，重力加速度设置为G=9.810 m/s2。然后再施加冷弯位移，根据设计冷弯曲率对应的冷弯位移在冷弯端施加位移边界条件。

3.4 模拟结果

对冷弯过程进行有限元模拟得到的玻璃板主应力位置与试验结果相一致，在A- 1面长边中点处出现最大的第1主应力σ1，同时，第2主应力极值则出现在固定端短边的1/4处。IG- 1、IG- 5以及IG- 9在A片玻璃上的主应力云图，如图11所示。

(a)IG- 1，A- 1面，ρ=1/24 000 mm-1

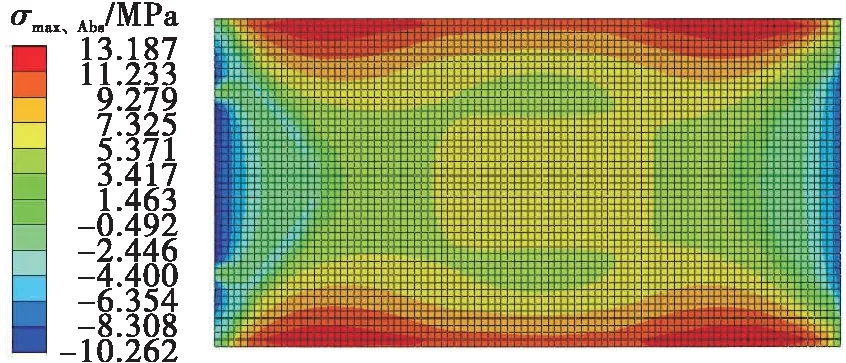
(b)IG- 1，A- 2面，ρ=1/24 000 mm-1

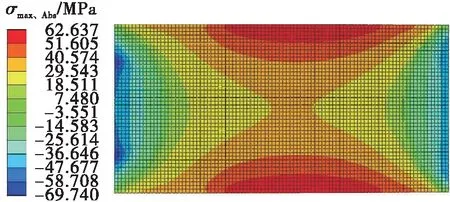
(c)IG- 5，A- 1面，ρ=1/12 000 mm-1

(d)IG- 5，A- 2面，ρ=1/12 000 mm-1

(e)IG- 9，A- 1面，ρ=1/18 000 mm-1

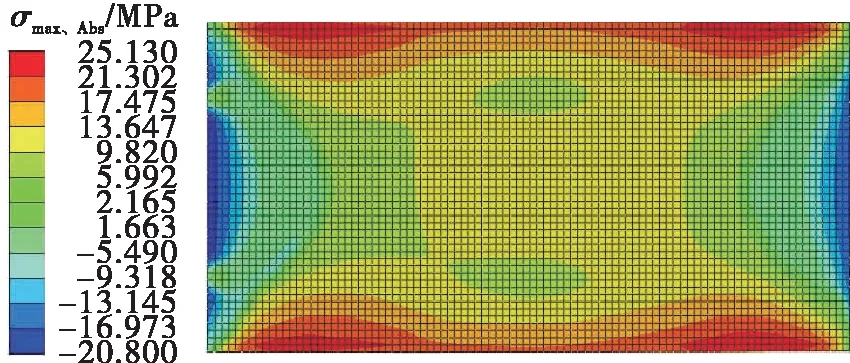
(f)IG- 9，A- 2面，ρ=1/18 000 mm-1图11 A片玻璃的主应力云图Fig.11 Principal tress nephograms of A-piece glass

与试验结果相对比，有限元模拟的主应力分布与试验所得的主应力分布大体相同，偏差范围在13.55%内，见表15。表中，σ1，FEA为试件A- 1面的模拟最大主应力，σ1，Test为试件A- 1面的试验最大主应力。表15说明有限元模拟的结果与试验结果相近，同时，模拟结果相对于试验结果而言，主应力值偏大。一方面是由于在有限元模拟中，丁基胶与铝隔条的相互作用的设置使用了连接刚度更大的“绑定”约束，这就造成玻璃板在边缘区域的刚度比实际更大，其主应力也更大；另一方面，实际试验中受力最大的A片玻璃外表面在冷弯后的曲率要比另一片玻璃的要小，因而试验中玻璃外表面的受力要小于理想冷弯边界状态下冷弯玻璃受力。虽然有限元分析结果稍偏于保守，但考虑到中空冷弯玻璃板的受力及边界条件更复杂，在设计中使用这一有限元分析方法还是满足设计要求的。

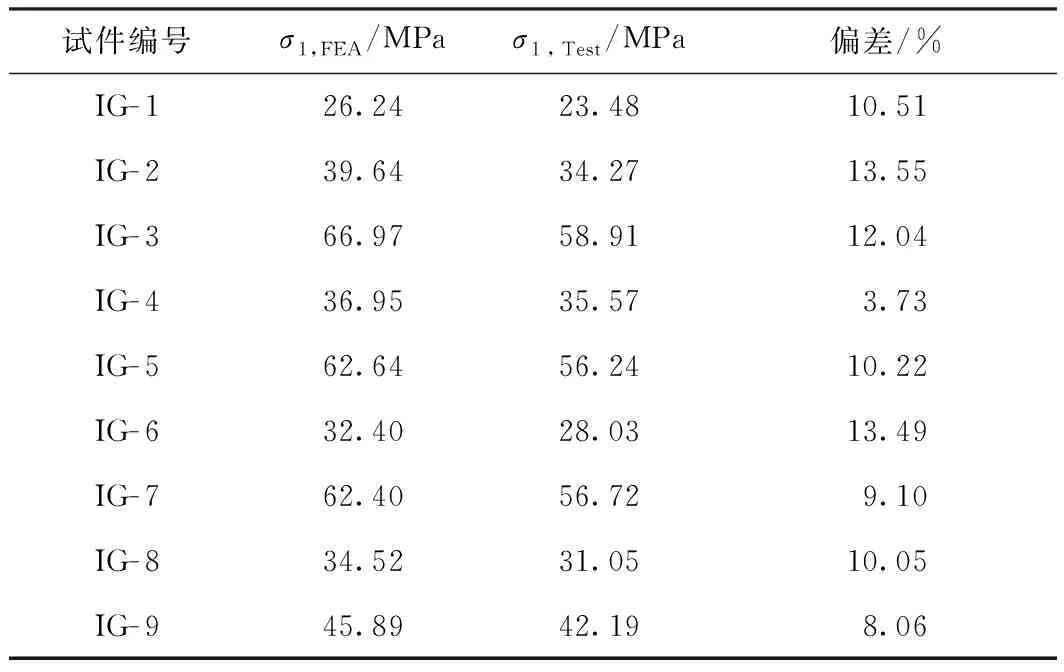
表15 A- 1面的最大主应力模拟值与试验值对比Table 15 Comparison between simulated and experimental va-lues of maximum principal stress on A- 1

4 结论

(1)中空玻璃板的单向冷弯主应力在不同玻璃板上的分布不均匀，玻璃板最大主应力出现在外凸面上，在该表面最有可能产生破坏应力，间隔条的约束作用会使得内表面的主应力极值点位置不在长边中点。

(2)冷弯曲率对中空玻璃板冷弯主应力的影响最明显，冷弯曲率增大会使得中空玻璃的变形加剧，同时所需的冷弯荷载也更大；而空腔厚度以及玻璃厚度的增大对中空玻璃板主应力的影响很小。

(3)采用硅酮胶和铝隔条作为间隔条的中空玻璃在冷弯时会产生层间位移，冷弯曲率、玻璃厚度和空腔厚度的增加，都会使层间位移有所增大，但层间位移主要受冷弯曲率的影响，玻璃厚度和空腔厚度的影响不大。

(4)所采用的有限元建模方法和材料参数能较好模拟试验结果，数值稍偏保守，在对冷弯中空玻璃板进行设计和施工时，可以采用有限元计算结果作为参考。