“学科育人”视角下的教学设计

陈华曲

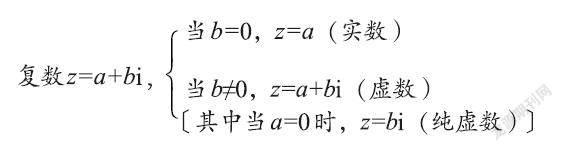
如何更好地落实数学学科育人目标？我们尝试以“思维育人、史料育人、审美育人、活动育人”四个维度为抓手，在数学教学各环节挖掘学科育人内涵，努力使数学教学从形式到内容都有“立德树人”目标的引领。本文以“数系的扩充和复数的概念”一课为例，谈谈自己的思考与实践。

一、新课引入

“新课引入”是一节新授课的基础，它的立意对调动学生学习的积极性十分重要，会影响整节课学生的关注度和参与度。本课以数学史为切入点，融入中外数学家的经典数学故事，以史料育人。

《道德经》有言：“道生一，一生二，二生三，三生万物。”

古希腊数学家毕达哥拉斯提出“万物皆数”，这节课我们就从数字“1”开始。

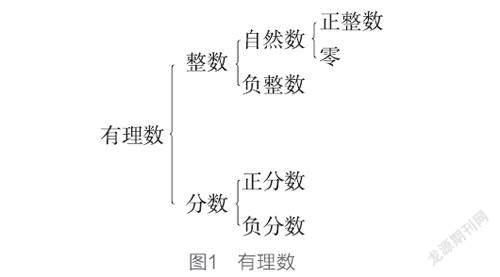
历史追溯到五万年前，人类在认识自然界的过程中，用手指、木棒、小石子来计数。随着语言的发展、生产和交换的增多，古人渐渐把数从具体事物中抽象出来，就有了数字“1”，以后逐次加1，就得到2，3，4，5，6……用“0”来表示“无”，“1”就是从无到有。这样就有了自然数集，自然数集包括正整数和零。

在历史的发展中，人们逐渐认识到仅有自然数是远远不够的，例如，1份猎物要平均分给2个人，每个人分到的猎物数该怎么表示呢？于是人们提出了分数的概念 。

随着生产的发展，产生了借贷关系中量的不同意义的需要。我国三国时期数学家刘徽曾说：“今两算得失相反，要令正负以名之。”首先给出了负数的定义、记法和加减运算法则。古代数学家们在研究中也常常遇到小数减大数的情况，负数的概念应运而生。于是数系从自然数、分数扩充到了有理数 （见图1）。

在公元前500年的古希腊，数学受到了前所未有的尊崇。毕达哥拉斯认为，万物发展的规律和秩序都遵循一些数学原则。这些秩序就是美的根源。他在音乐的世界里，通过测量音阶振动的弦长，发现最美的三个音阶的弦长分别是2∶1，3∶2，4∶3。他兴奋地认为世界的秩序都能由整数和整数之比来掌控、调节。毕达哥拉斯还在有理数的世界中证明了毕达哥拉斯定理（即揭示直角三角形三边关系的勾股定理）。但是，他的学生希帕索斯发现边长为1的正方形，对角线却无法用整数或分数来表达，于是无理数开始登上历史的舞台。数系扩充到了实数。

【设计意图】本节课是高中阶段完成的最后一次数系的扩充，复数是高中数学非常重要的一个知识点。我们从数学的起源开始，用大量的史料引入，让学生回顾每一次数系扩充的历史背景，使数学教学与数学学习不枯燥、不乏味，在扩充学生的眼界、提高学生学习热情的同时，也增强了数学课堂的文化体验。加入史料教学可以使学生不走弯路，更深刻地理解教材中的知識点以及文化内涵，明白自己解决不了的问题与前人不解的问题有一致性，从而不惧怕数学。以史料怡情，以史料育人。

二、概念形成

“概念形成”是一节课的重点，它对学生构建自身的认知结构起关键作用。这一环节的重要任务就是让学生理解概念形成的合理性。本环节通过六个问题的层层推进，让学生经历发现问题、思考问题、解决问题的过程，一步一步接近复数。

我们用一个解方程的过程再次演示数系扩充的必要性。

方程x+1=0在自然数集中无解，添加新数（负数）后，解为x=−1，自然数集扩充到整数集。方程2x‒1=0在整数集中无解，添加新数（分数）后，解为x=，整数集扩充到有理数集。方程x2‒2=0在有理数集中无解，添加新数（无理数）后，解为x =±，有理数集扩充到实数集。

问题1：几次数系的扩充有什么共同点？

共同点有以下几个方面。

扩充的方法：在原有的数系中添加新数。

扩充的规则：添加新数后，原来的运算和性质仍然适用。

扩充的效果：解决了原数系中不能解决的运算。

通俗地说，每一次数系的扩充都是因为原数系中的数“不够用”了。

【设计意图】问题1意在帮助学生重新构建数集的扩充过程，是本节课的生长点。教师要让学生了解每个数的产生并不是从天而降，而是数学内部发展的需要。教师通过对前几次数系扩充的梳理，让学生感受到数系扩充的合理性，并归纳、概括、提炼出数系扩充的一般原则，为数系的进一步扩充以及如何扩充打下坚实的基础。

问题2：在方程运算中，实数系是否“够用”？你能举一个例子吗？

生：不够用。如在实数范围内，方程x2+1=0，x2=−2，x2=−3无解。

师：所以数系还需要扩充！接下来我们就以一元二次方程为背景，一起来研究数系应该如何进一步扩充。请大家通过配方法把以下一元二次方程转化为的形式。

① x2  + 2x + 1= 0（x+1）2 =0x=−1。

② x2  ‒ 2x + 5= 0（x ‒ 1）2 =−4在实数集中无解。

③ x2  + 2x ‒ 8= 0（x+1）2 =9x1=2，x2=−4。

问题3：所有的一元二次方程都可以转化为（x‒a）2=k的形式，通过这个形式，如何判断一元二次方程在实数范围内无解？

生：只需要关注k的取值就可以了，k<0时，方程在实数范围内无解。

师：当k<0时，方程在实数范围内无解。为了解决这个问题，我们需要对数系进一步扩充。根据数系扩充的方法，首先，我们得添加一个新数。

【设计意图】问题2的设问生活化、平易近人，减轻了学生的畏难情绪。问题3精准设问，以在实数范围内无解的一元二次方程为背景，寻找出最简单的条件，归纳出无解的原因。数学学习需要寻根溯源，不能脱离背景孤立地学习某一个知识点，而要想方设法呈现与这个知识点相关联的东西，挖掘隐含在背后的数学本质，让学生的认知形成一个整体。在生活中遇到难题也要学会从源头找原因，这样才能想出最简单、最有效的解决方法。以数学理性思维育人。

问题4：数系的扩充需要添加“新数”，要使（x‒a）2=k（k<0）有解，我们添加的“新数”要具备什么功能？

生：要使新数的平方等于一个负数！

师追问：如果我们要定义某个数的平方等于一个负数，当k取不同的值时，我们是否需要定义无数次呢？

生甲：好像是需要添加无数个新数才行。

生乙：不需要添加无数个新数。当k取不同的负数时，我们都可以把k写成−1×（−k）的形式，然后方程x2 =k（k<0）可以轉化为=−1（k<0），我们只需要定义一个新数的平方等于−1就可以了。

师：数学定义应该简明，同学乙给出了一个很好的思路。我们只需要定义一个数的平方等于−1就可以了。那么这个数应该用什么符号来表示呢？

生：既然是符号，就没有特别的规定，如果让我穿越到过去，我希望用一朵小花来表示这个数，不知道可不可以。

师：我想应该没有大问题。引入新数，我们尊重历史习惯吧。这个新数用一个字母符号“i”来表示。历史上，新数i是瑞士数学家欧拉在1777年首次提出使用的，他用了“imaginary（本义是虚幻的）”一词的首字母。

【设计意图】问题4培养学生的类比和迁移能力。“追问”意在沿着“专注—直觉—分析—权衡”的思维路线，让学生突破直觉，寻找出更全能的解决办法。教师要让学生体会到引入一个新数，不是要解决一个问题，而是要解决一类问题。最有价值的知识，是方法的知识。数学问题的设置要从学生的最近发展区入手。最近发展区有利于发展学生思维品质，培养学生知识迁移能力，引导学生从新的角度看问题，培养创造性思维。

问题5：定义了i2=−1，你能否写出方程（x‒1）2 =−4的解？

解法如下：

=i x=12i

追问：定义了i2=−1，你能否写出方程（x‒a）2= k （k<0）的解？

解法如下：

师：在表达式中，a为实数，也是实数，那么我们就可以把表达式记为x=a+bi，这样在结构上能够更简洁，数学就讲简洁美。

【设计意图】学生在参与和体验数学知识的发生和发展过程之后，就可以运用数学知识及其思想方法对具体问题进行分析研究，对数学结论产生顿悟和灵感，提高运算求解能力，增强成功的体验。

问题6：实数a能否写成a+bi的形式呢？

生：b=0时，a+bi=a，即a=a+0i。

师：由于i的加入，实数集可以扩充到一种新的数集，我们把形如a+bi（a，b∈R）的数叫作复数。把集合叫作复数集。

【设计意图】从实数表达式过渡到复数表达式，如何才能满足代数表达式在结构上的统一性？这是一个看似简单却需要点拨突破的问题。数学的内在本质是统一、和谐的。教师在学生豁然开朗的同时给出新概念，让学生自然而然地习得新概念。

三、概念深化

“概念深化”是一节新授课的灵魂，它直接影响了学生能否以更高的观点去看待问题。这个环节要善于挖掘概念的内涵、外延，培养学生的数学核心素养。

根据数系扩充的“包容性”原则，添加的新数i也可以跟实数进行四则运算。

问题7：你能从运算的角度解读复数a+bi（a，

b ∈R）的结构特征吗？

生：从结构上看，复数可以看作由两部分组成，一部分是一个实数a，另一部分是一个实数b与i相乘，那么a+bi就可以看成一个实数a加上实数b乘i。

师：复数通常用字母z表示，即z=a+bi（a，b∈

R），这一形式叫作复数的代数形式。a叫作复数的实部，b叫作复数的虚部，i叫作虚数单位。

问题8：把实部和虚部特殊化，复数如何分类？

师：我任意写出6个复数，两两分成一组，你会怎么分组呢？例如，3，4+5i，3i，−2i，−2−4i，6。

生：3和6为一组，4+5i和−2−4i为一组，3i和−2i为一组。

根据分组，学生很快就能总结出复数的分类。

显然，实数集R是复数集C的真子集，即RC。（在黑板上画出韦恩图）

类比实数的性质，我们一起来研究复数的性质。

【设计意图】问题7让学生剖析复数的代数形式，透过结构特征揭示数学本质，体会数系扩充后其内在方法和思想的一致性。问题8通过复数的分类，揭示出统一的数学结构中不同的数学个性。在强化新知的同时，培养学生个性和共性的辩证统一思维：一个有人格的人，必定是社会化和个性化相统一的人。再次渗透数学思维育人。

问题9：如何确定一个复数？

我们可以从两个维度来看两个复数是否相等：实部是否相等，虚部是否相等。也就是说，当两个复数的实部、虚部都相等了，这两个复数就相等，即复数由它的实部和虚部来确定。因此可以说复数是一种二维数。

追问：如何判断两个复数相等？

在复数集C中，任取两个数a+bi，c+di（a，b，c，d∈R），我们规定a+bi和c+di相等的充要条件是a=c且b=d。

追问：复数能比大小吗？

生：不能比，因为复数是“二维”的数，“二维”的数不能比大小。

师：如果复数的虚部为0，那么复数就是实数了，实数能比大小吗？

生：应该补充一下，当复数是实数时，可以比大小;但当复数是虚数时，就不能比大小了。

【设计意图】问题9以及“追问”引导学生学会多角度思考和理解概念的本质特征，引导学生找出微小的不同点加以分析。这对培养学生思维的深刻性有着很高的价值。教师在教学时使用对比效应可以刺激学生的大脑，让学习更轻松。

问题10：实数是一维的，它与数轴上的点一一对应。复数是二维的，它的几何意义是什么？

师：这个问题请同学们课后思考，这是我们下节课需要研究的内容。

【设计意图】从几何意义的角度给学生抛出问题。小小的遗憾能带来大大的思考，也为后续知识的连贯性做好铺垫。

师：经过这几个问题的研究，相信同学们对复数有了进一步的认识，接下来我们通过几个例题来检验强化新知。

四、应用探索

“应用探索”是新授课的关键，也是学生数学学习的根本目的之一，它对学生能否灵活运用知识关系重大。这一环节教师要教会学生从正确的解题思路中总结方法，提高对数学思想的理解能力。

练习1：实数m取何值时，复数z=m+1+（m‒1）i是（1）实数？（2）虚数？（3）纯虚数？

练习2：说出下列复数的实部和虚部。

i，i，，，i，0

练习3：指出下列各数中，哪些是实数，哪些是虚数，哪些是纯虚数，为什么？

2+，0.618，i，0，i，5i+8，3‒，

i（1‒），

练习4：如果（x+y）+（y‒1）i=（2x+3y）+（2y+1）i，求实数x，y的值。

【设计意图】数学解题中学生时而“惊心动魄”，时而“深陷绝境”，时而“绝处逢生”。只有经历了解题的过程，学生才能提高解题能力。学生在快速解答的过程中，很容易出现“想当然”的错误，及时纠正，实现数学教学的知行合一，践行数学课堂实践育人。

五、总结归纳

“总结归纳”是一节新授课的升华 ，它对学生能否深入理解新知识的重点、能否构建起知识网络，起着十分重要的作用。教师要精心设计课堂总结，让学生真正获得提高，从而对整节课产生充实、愉悦的感受。

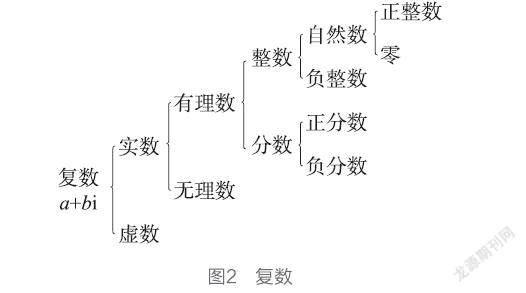
师生共同完成了一次新的数系扩充，学习了复数的结构特征（见图2）。

图2 复数

师总结：短短40分钟我们就完成了数系扩充，那是因为我们站在了前人的肩膀上，接下来我们一起看看复数的发展历史。

1545年，意大利数学家“怪杰”卡当第一次开始讨论复数开平方的问题，当时复数被他称为“诡辩量”。

1637年，法国数学家笛卡尔才把这种虚幻的数命名为“虚数”。

1777年，欧拉说这种数只存在于“幻想之中”，并用“i”来表示它的单位。

1832年，德国数学家高斯把复数看作复平面的点，使之通行于世。

现在看起来简单的数系，它的发展却经历了各种艰难，数学的发展如同数系的发展一样，需要几代数学家长时间的努力才得以完善！

任何新事物的产生都不能迅速地被人们接受，它必然会受到旧事物的阻挠。数学家们追求真理、献身科学的精神深深地影响着我们！

【设计意图】回顾数系扩充的发展顺序，让学生对本节课究竟学习了什么内容有一个更充实、饱满的認识。展示复数近三百年的发展历史，能够让学生体会到在漫长的历史时期，复数的创立是需要创新精神的，数学家们要敢于向传统观念挑战，更要有锲而不舍的精神。课堂最后再次加强数学文化育人，让学生回味无穷。

（作者单位：广西壮族自治区南宁市第三中学）

责任编辑：赵继莹