三相逆变器控制策略的研究与仿真分析

靳舵，张厚升，李家琪，蒋俊杰，王 傲

（山东理工大学电气与电子工程学院，山东淄博 255022）

0 引言

在经济全球化的大背景下，人类社会取得进步的同时也面临着资源消耗过快的问题，这也给环境造成了很大的污染［1］。燃油汽车行业受到了巨大冲击，面对这种严重问题不得不做出调整。近年来，电动汽车（Electric Vehicle，EV）凭借其污染少、能量利用率高、噪音小以及能量可回收等优点在我国得到了大力支持和迅速的发展［2-3］。

研究发现，电动汽车每天集中使用的时间有限，绝大部分阶段保持停放的状态。经众多学者研究，一种车网互动技术（Vehicle to Grid，V2G）蓬勃发展，在用电高峰期时，为满足高负荷用电需求，将电动汽车的电能回馈至电网，这也表明了电动汽车可对智能电网起到削峰填谷的作用［4-6］。

三相逆变器是电动汽车V2G技术的重要环节，在实现调节电网波动，进行削峰填谷的同时，又要避免电力电子设备所引起的谐波以及无功功率对电网的影响［7-8］。对三相逆变器的控制策略的研究，文献［9］中不再使用传统的PI控制而是引入了模糊逻辑控制，获得了高功率因数和低谐波畸变的效果，动态响应较快但控制精度有待提高。文献［10］中引入基于电压和电流前馈解耦的双闭环控制，控制效果较好，但变换过程较为复杂，且没有对直流电压进行控制。文献［11］中将滑模变结构控制应用到电压外环，通过该算法为内环提供电流，控制精度高且响应较快，但在跟踪输入电压时存在着较大的电流波动。文献［12-13］中提出电流预测控制策略，能使电流迅速达到给定值，该控制方法具有较高的功率因数，谐波含量少且能保持直流侧电压的稳定，但计算复杂、动态性能较差。

三相逆变器可将电动汽车中的直流电转化为交流电，实现对电网的削峰填谷，这对电网波动的调节具有重要意义［14-16］。本文主要研究三相全桥逆变器的控制策略，调制方式采用结构简单且容易实现的正弦脉宽调制（Sinusoidal Pulse Width Modulation，SPWM）。以三相全桥逆变器为研究对象，建立其数学模型，提出一种基于前馈解耦的双闭环控制策略。仿真结果证实了本文所提的控制方法可有效地提高直流侧电压的控制精度，减小并网电流的波动及降低谐波畸变。

1 三相逆变器的数学模型

在实际应用中，三相逆变换器可将电动汽车电池中的直流电转化为交流电，在智能电网不稳定的时候对其进行调节，实现削峰填谷的作用。本文主要基于三相全桥电压型逆变器的电路结构进行研究，其结构如图1 所示。

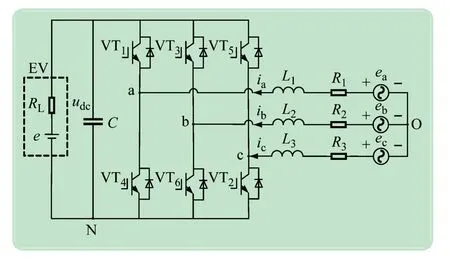
图1 三相逆变器电路结构图

图中ea、eb、ec为三相交流侧的输入电动势，ia、ib、ic为三相交流侧的输入电流，R1～R3、L1～L3分别为电网侧等效电阻和等效电感，VT1-VT6为开关管器件，C为直流侧储能电容，udc为电容两端的电压，e为直流侧电动汽车电池的电动势，RL为直流侧电阻。

由图1 的电路结构可得出，该三相全桥逆变器共采用6 个开关管，存在3 个桥臂。本文采用逻辑函数Si（i＝a、b、c）的数值分别表示对应桥臂上两个开关管的工作状态。当Si的值为1时，表示该桥臂上端的开关管导通，下端的开关管关断；当Si的值为0时，表示该桥臂上端的开关管关断，下端的开关管导通。

为便于分析和研究，假设三相交流电动势ea、eb、ec为幅值相同、相角互差120°的正弦电势；电网侧各相等效电感和阻值相同，即R1＝R2＝R3＝R，L1＝L2＝L3＝L；VT1-VT6均为理想的开关管。利用基尔霍夫电压定律（KVL）与电流定律（KCL）可得该逆变器在三相静止坐标系下的模型

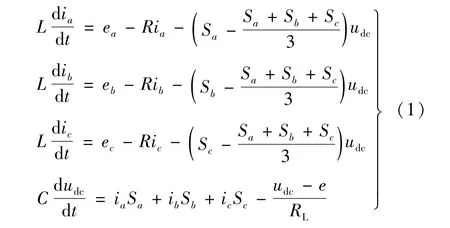
在三相静止abc 坐标系下，逆变器的各变量均为交流量，很难进行相关的计算和控制，使得控制系统设计困难。为简化控制运算，将逆变器模型转化到两相同步旋转dq坐标系下，使交流变量等效为直流变量。为简化计算，引入坐标变换矩阵

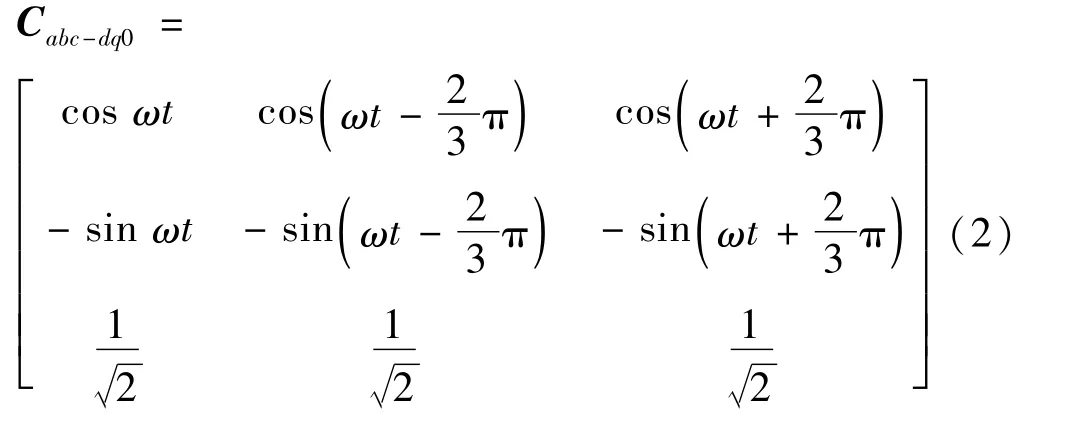
式中：ω为旋转角转速；ωt为a轴与d轴之间的夹角。当时间t为0时，a轴与d轴重合。

结合式（1）、（2），该逆变器的模型可转化到两相同步旋转dq坐标系下，

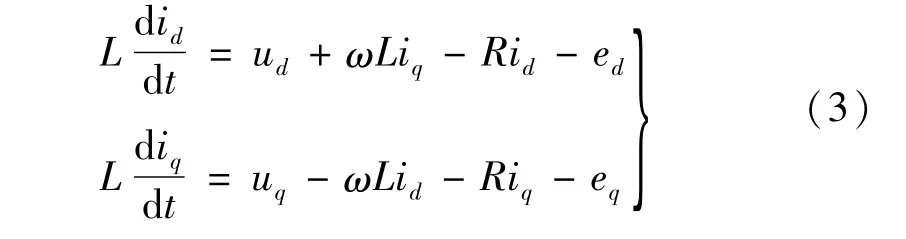
式中：ud和uq分别为三相逆变器交流侧电压的dq轴分量，id和iq分别为三相逆变器交流侧电流的dq轴分量，ed和eq分别为电网电动势的dq轴分量。

在两相同步旋转坐标系下，三相逆变器模型的dq轴电流分量id与iq可分别表示交流侧电流的有功分量与无功分量，因此对电流id与iq进行控制就可以实现对交流侧有功和无功的单独调节。由式（3）可知，在dq轴上的电流分量id和iq受多种变量的影响，且均含有d、q轴上的参数变量，存在着复杂的耦合现象，因此设计控制策略时应首先将d轴与q轴间的耦合现象解除。

2 基于前馈解耦的双闭环控制策略

由于电网侧等效电阻非常小可忽略，即式（3）中的Rid与Riq可以忽略不计。电流环控制器采用PI控制器进行调节，所以式（3）中的电流微分项可由PI 控制器获得，其他的扰动项采用前馈补偿的方法运算，可得电流控制方程

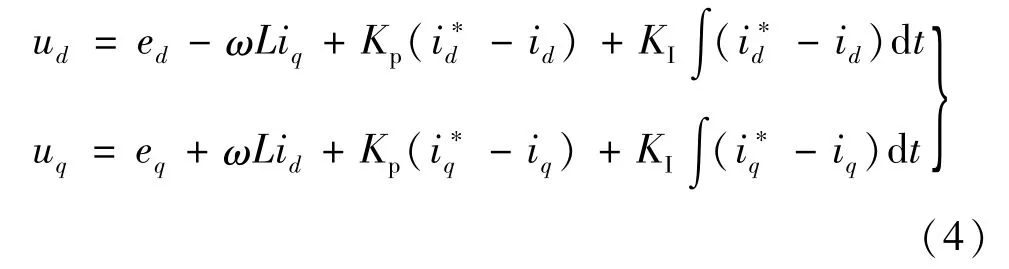
将式（4）代入式（3），可得

由式（5）可见，三相逆变器在两相同步旋转坐标系下的电流分量id和iq已经实现完全解耦。基于两相同步旋转坐标，图2 给出了该控制策略的前馈解耦框图。

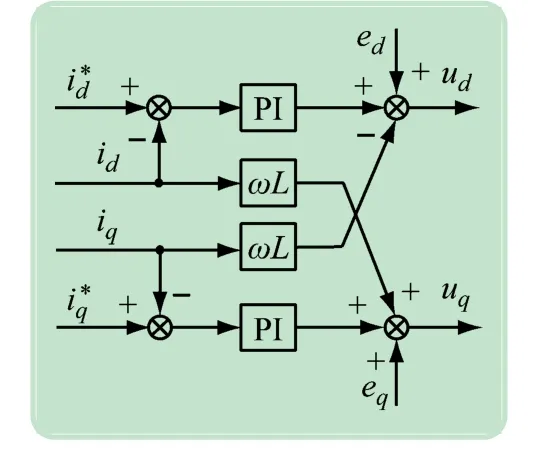
图2 两相同步旋转坐标前馈解耦控制框图

在前馈解耦过程中，由于id、iq中存在电流脉动分量，这会对控制过程产生不利影响。为提升控制效果，将参与前馈解耦的dq轴电流用给定的dq轴电流替换。通过电流环的前馈解耦环节，消除了电流分量id与iq之间的耦合现象，对两者分别进行控制即可实现对有功功率和无功功率的单独调节。如图3 给出了电流替换后的前馈解耦控制框图。

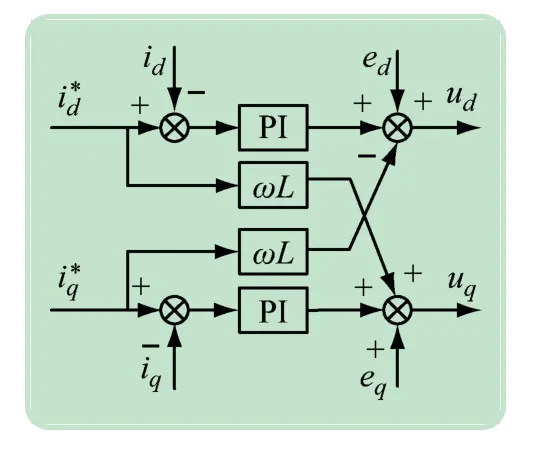
图3 改进的前馈解耦控制框图

为并网过程能高效运行，引入锁相环（Phase locked loop，PLL）来跟踪电网侧三相交流信号的相位信息，图4 给出了锁相环控制框图，其中：f为电网电压的频率；θ为交流信号的相位角度。

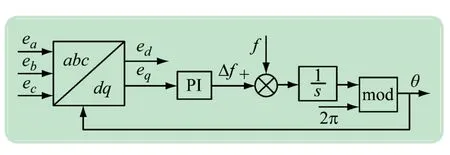
图4 锁相环控制框图

锁相环主要由3 部分组成，分别为鉴相器（对应坐标变换）、滤波器（对应PI 控制器）以及压控振荡器（对应积分环节）。三相电压经变换后可分别得到其在dq轴上的电压分量，将q轴的电压分量经过PI 控制器进行调节，输出频率的差值与电网电压频率求和并进行积分，最终得到交流侧信号的相位角。

图5 给出了改进的基于前馈解耦的双闭环控制策略结构图，图中为直流侧电压给定值。该控制策略具有良好的控制性能，能保证交流电网侧以及直流侧具有良好的静态特性。

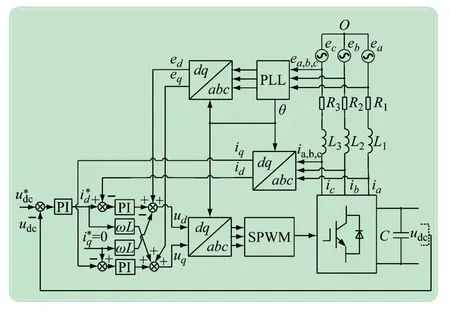
图5 电压电流双闭环控制结构图

该控制方法将三相交流侧的电压和电流经坐标变换转化到dq轴上所对应电压、电流分量，作为前馈解耦控制的输入信号。电压环与电流环均采用PI 调节器进行控制，电压外环能使直流侧电压保持稳定，电流内环通过调节器维持电流的稳定。电压给定值与反馈值进行比较计算，将偏差作为PI 调节器的输入，将所得运算结果作为d轴电流分量的给定，根据解耦与经变换得出的dq轴电压与电流分量以及参数ωL进行前馈解耦运算，得到调节后的ud；为保证三相逆变器具有良好的工作特性，实现功率因数为1 的运行效果，电流在q轴分量的给定值设置为零，同理可以得到调节后的uq值。将所得的dq轴电压分量转化到三相静止坐标系中，经过SPWM 环节输出6 脉冲的PWM波形，该控制信号通过控制6 个开关器件的通断使得逆变器高效运行。该控制方法能够实现变换器在功率因数为1 的状况下运行，使得控制系统动态性能较好，具有良好的稳态效果。

三相逆变器作为连接智能电网和电动汽车的重要枢纽，要能从直流侧向交流侧馈送能量，且在逆变过程中尽可能减小对电网的谐波污染。在用电量较大的时间内，为保证智能电网的稳定状态，需将电动汽车侧的电能反馈到交流电网，通过增大直流侧电压值udc使其大于电压外环给定值，即-udc＜0，该偏差值经过PI调节器输出一个负的给定q轴电流分量，此时逆变器开始工作，向交流电网侧释放能量，且在变换过程中产生的谐波对电网的影响较小，具有良好的应用前景。

3 仿真结果分析

为验证本文所提控制策略的有效性，达到电动汽车对智能电网削峰填谷的调节目的，完成能量从电动汽车向电网的馈送。通过建立三相逆变器，在Simulink中进行了仿真，表1 给出了仿真系统的主要参数。

表1 系统仿真参数

由图1 双向变换器电路结构可知，该系统共有3个桥臂，分别对应开关管VT1和VT4、VT3和VT6、VT5和VT2。开关管在接收到控制信号时并不能立即达到控制效果，同一桥臂上的两个开关管可能会同时导通致使危险现象的发生。为避免这一情况，在PWM 信号生成之后加入了一个开通延迟环节，当给定开通信号时，开关管会延迟一段时间导通，这就保证了开关管能够安全导通，消除了安全隐患。延迟后的PWM 脉冲信号波形如图6 所示。

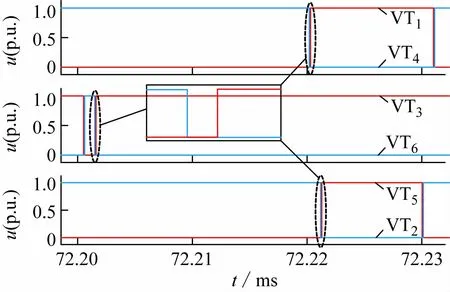
图6 PWM脉冲信号波形图

当电网处于高负荷状态下，电动汽车经逆变器向智能电网提供能量，将电动汽车一侧的直流电转化为交流电进行并网。图7 给出了逆变过程中直流侧电压的仿真波形，其中蓝色表示为传统双闭环控制策略，红色为本文所提控制策略。可见，直流侧电压经过调节均可以达到稳定状态，两者均在0.1 s左右稳定在600 V，具有良好的动、静态效果。在传统控制方法中，直流电压降落达到545 V，本文所提控制策略电压降落约到555 V，其电压降落更小。从稳定状态的局部放大图可以看出，在传统控制下，直流侧电压在599.95 V上下波动，波动范围为0.2 V，而在本文所提控制策略下，直流侧电压稳定在600 V，其波动范围为0.2 V，具有更优良的控制精度。

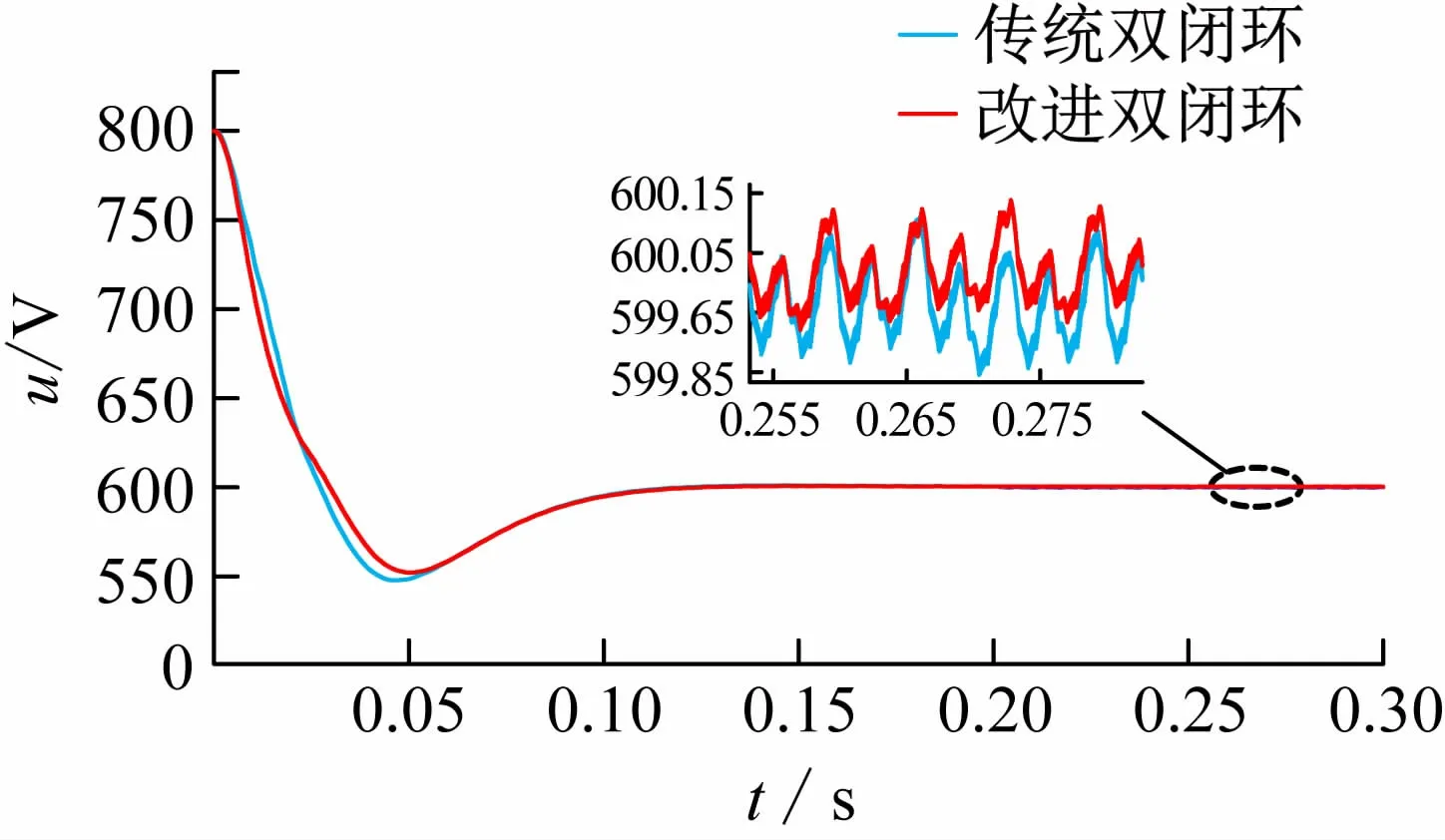
图7 直流侧电压波形

图8 给出了逆变过程中三相交流侧电压及电流波形。当三相逆变器处于稳定状态时，并网电压与电流均保持为稳定的正弦波，其中电压的幅值约为310 V，电流幅值约为17 A。图9 给出了A 相电压与电流的波动情况。可以明显看出，电压与电流始终保持着相反的相位关系，这也表明了此时电动汽车处于向电网放电的状态。

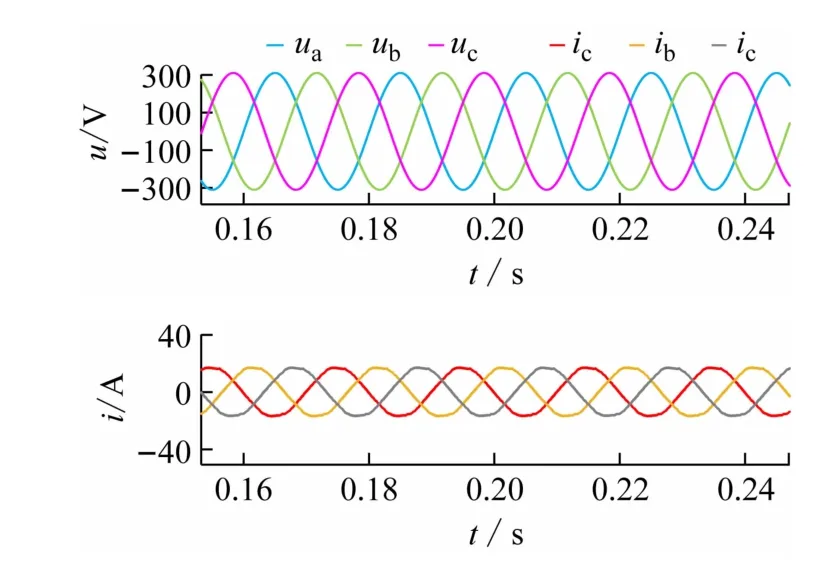
图8 三相并网电压、电流波形

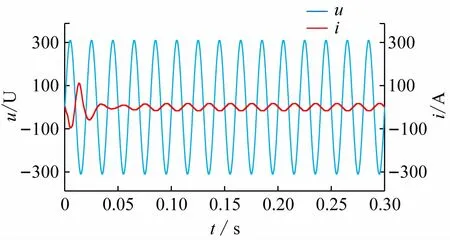
图9 a相并网电压、电流波形

图10 给出了逆变过程中不同控制策略下交流侧并网电流的波形。两种控制方法在经过0.08 s 的调整之后，均达到稳定的正弦波形。但调节过程中，本文提出的控制策略具有更小的电流冲击，约在-95 A到110 A范围内调节，而传统的控制策略在-110 A 到110 A内调节。在逆变过程中，改进的控制策略并网电流冲击更小，对电网有着更小的影响。

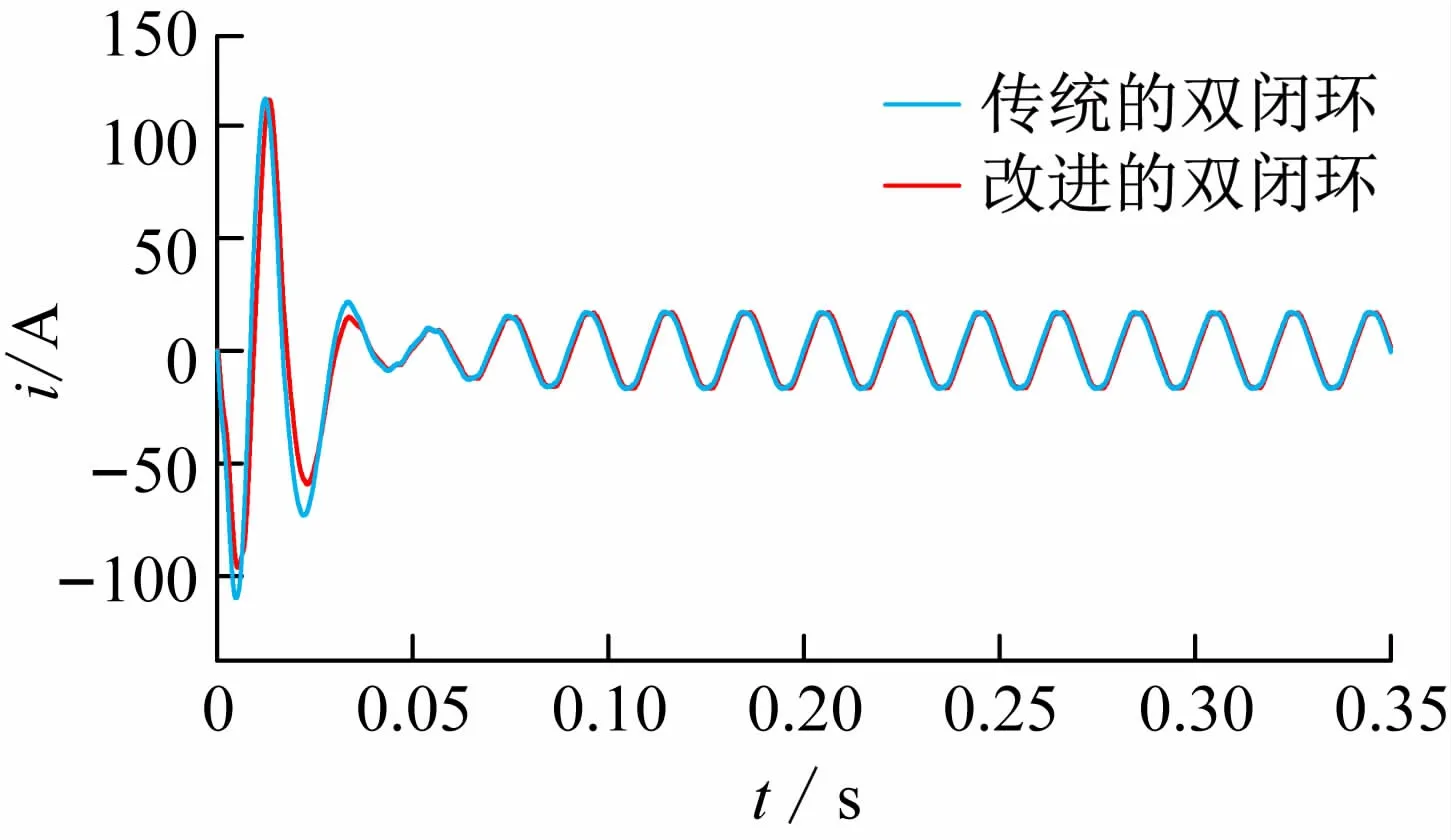
图10 交流侧电流波形

图11、12 分别给出了传统控制策略和改进的控制策略下a相电流的频谱，其总谐波失真分别为3.56%和2.74%，均小于5%。所提控制策略的谐波含量较传统的控制策略减少0.82%，并网电流的质量更高，使得整个逆变系统更加稳定，逆变过程对电网的影响更小。

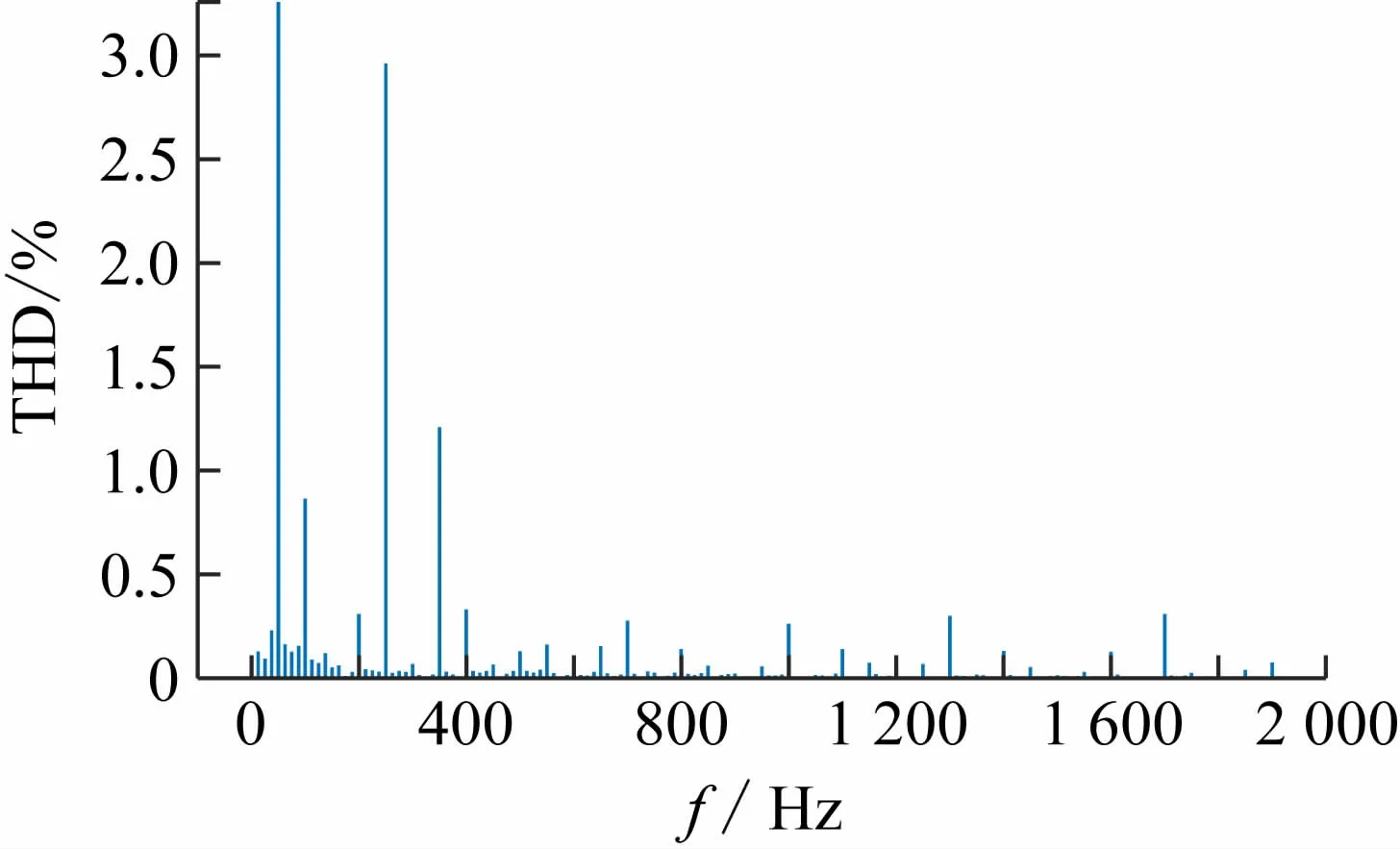
图11 传统控制策略下并网电流谐波分析

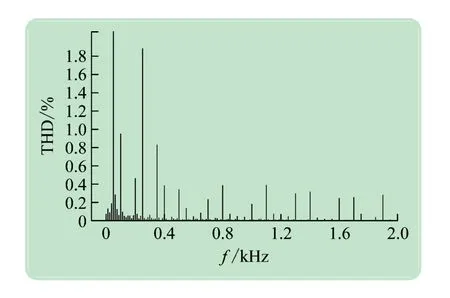
图12 改进控制策略下并网电流谐波分析

4 结语

三相逆变器是联系智能电网与电动车的重要环节，其逆变过程的控制效果直接决定着电动汽车蓄电池向智能电网馈送能量的效率，实现对电网的填谷作用，在减小电网波动等方面具有重要意义。本文对三相逆变器的数学模型进行了介绍，基于对dq轴坐标系下前馈解耦控制方法的研究，提出一种改进的电压、电流双闭环控制策略，使系统在功率因数为1 的状况下运行，提高系统的控制精度和稳定性，降低并网电流的畸变。通过对系统的仿真分析，表明了该控制策略的可行性，在逆变过程中减小了直流侧电压的波动，并网电流冲击更小，谐波含量也有明显减少，取得了良好的控制效果。