一种基于Ansoft Maxwell 开关磁阻电动机调速系统建模方法

丁晓军，赵 涛，马 琴，刘 锋，虎 鑫

（1.北方民族大学 a.电气信息工程学院；b.机电工程学院；c.土木工程学院，银川 750021；2.共享智能装备有限公司，银川 750021）

0 引言

开关磁阻电动机调速系统（SRD）是一种新型的调速装置，通常由开关磁阻电动机（SRM）、功率变换器、电流检测装置、位置检测装置及控制器5 部分组成。SRM由于结构简单、起动转矩大、成本低廉以及调速范围宽的特点，已经在油田、煤炭工业、家用电器、机床设备等领域得到了广泛的应用［1-5］。

然而，由于SRM定、转子采用双凸极结构，其运行过程中存在明显的边缘效应和局部饱和，SRM 磁路表现出高度非线性，采用简单的线性化模型来描述其静、动态特性，误差较大。同时，SRD 是由SRM、功率变换器、电流检测、位置检测和控制器的统一体，为了精确研究SRD的静、动态特性，势必要建立SRM的非线性模型。为此，针对SRM 的非线性建模，学者们开展了相关研究［6-10］。纪志成等［11］利用Matlab 将SRM 磁化特性曲线的饱和段与非饱和段分别线性化，来近似逼近非线性磁化曲线，建立了SRM 的非线性模型，这种处理方法优于简单的线性化模型，但这种分段线性化的方法依然会带来误差；李晓艳等［12］采用分段解析式描述电感的非线性，建立了SRM 的非线性模型；程勇［13］利用Matlab自带的SRM 非线性模型，建立SRM的非线性模型。

本文利用电磁场有限元分析软件Ansoft Maxwell 2D得到SRM 的电磁转矩数据和磁化曲线，结合Matlab／Simulink电气系统模块库（Power System Blockset），对其自带SRM模型分析的基础上，建立了SRM的非线性模型，进而实现了SRD的非线性建模与仿真。

1 基于Rmxprt的SRM建模

采用的SRM 电动机结构尺寸如下：相数为3；定子极数Ns＝12；转子极数Nr＝8；转子极宽bpr＝12.2 mm；转子轭高hcr＝8.5 mm；转子极弧βr＝16 mm；定子外径Ds＝154 mm；铁芯长度la＝105.6 mm；定子极宽bps＝11.6 mm；气隙g＝0.4 mm；定子轭高hcs＝7.5 mm；第2 气隙gr＝12 mm；定子极弧βs＝15 mm；轴径Di＝48 mm；转子外径Da＝88 mm；线圈匝数N＝138；定子、转子冲片材料型号为50W470。

通过以下5 个步骤建立SRM 几何模型：①建立Rmxprt模型，选择电动机型号；②选择电路类型；③输入电路初始电动机结构尺寸；④确定SRM 冲片材料；⑤设定求解器。

2 基于Maxwell 2D的电动机特性分析

将RMxprt设计好的几何模型，导入Maxwell 2D，基于静态求解器，通过设置边界条件、激励源对网格进行剖分以及添加计算参数，得到不同电流作用下，1 个电周期内的电动机绕组磁链和电磁转矩，如图1 所示。当电动机在0°时，给A相通电，绕组磁链一开始随着电流的增大呈线性增长，当电流增大到足够大时，磁链饱和。一个磁链变化周期对应的机械角范围为0～22.5°，如图1（a）所示。当转子从0°转到22.5°时，给绕组通电，会产生正转矩；当转子从22.5°转到45°时，给绕组通电，会产生负转矩，如图1（b）所示。

图1 不同电流作用下，单一电周期内电动机绕组磁链和电磁转矩

将最终得到的绕组磁链和电磁转矩数据以*.dat格式输出，分别存储到Excel中，为下一步SRD的建模和仿真提供数据。

3 基于Matlab／Simulink 的SRM建模

本设计使用的Matlab 版本是Matlabr2012b，该版本包含的SRM模型有三相6／4、四相8／6 和五相10／8结构3种，并不包含三相12／8 结构的SRM。此外，Matlab自带的SRM 模型中的电气转换环节均采用函数来实现，该类函数均以p文件形式存放，程序源文件无法获取，因此依赖Matlab自带的SRM模型实现上述功能是不可行的。为此，在深入剖析Matlab 自带SRM模型建模过程的基础上，建立了SRM 非线性模型，为SRD的建模和仿真提供条件。

SRM模型采用查表来实现。首先，测得绕组两端的电压，得瞬时电压Ux（x＝A，B，C）；其次，根据SRM的电路方程计算此时的磁链，通过SRM机械方程计算此时的转子位置θ，查表ITBL（1 个电周期内的电动机绕组磁链数据），得此时的相电流ix（x＝A，B，C），根据转子位置θ和相电流ix（x＝A，B，C），查表TTBL（一个电周期内的电磁转矩数据），得到此时SRM 的电磁转矩；最后，根据SRM机械方程计算得转矩和转速，SRM的非线性模型如图2 所示。

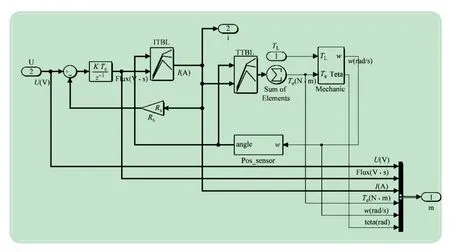
图2 SRM非线性模型

该SRM 非线性模型包含U（绕组端电压）和TL（负载转矩）两个输入，i（绕组电流）和m（SRM输出参数）两个输出，主要由转子位置角计算模块（Pos_sensor）、位置和转速计算模块（Mechanic）、转矩计算模块（TTBL）和电流计算模块（ITBL）组成。

3.1 转子位置角计算模块

转子位置角计算模块用于计算电动机各相转子的当前位置，其模块构成如图3 所示，输入为转子的转速，输出为当前转子的相对位置。转子角速度ω 单位换算成（°）／s，然后通过离散积分器得到三相对应位置，每一相与对齐位置均相差15°。因为在Ansoft Maxwell 2D中分析SRM时，定义通电顺序A-B-C-A（顺时针）为转子正转方向，所以A、B、C初始相对位置角应分别设置为0°、30°和15°，即B相滞后A相15°，C相超前A相15°。每一相角度值对45°求余后得其0°～45°内的角度值。

图3 转子位置角计算模块构成

3.2 位置和转速计算模块

位置和转速计算模块主要用来计算SRM 转子转过的总角度θ及其转速ω，其模块构成如图4 所示，输入为SRM的电磁转矩Te和负载转矩TL，输出为SRM的转子转过的总角度及其转速，其中转速ω根据SRM转矩方程求得。

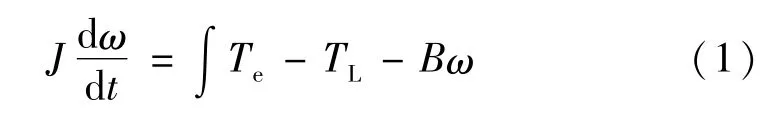
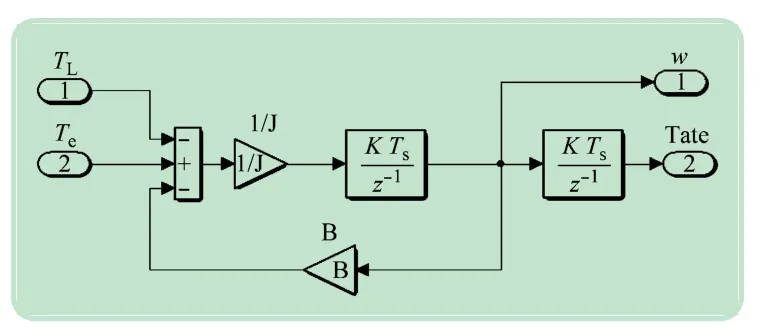
图4 位置和转速计算模块构成

3.3 电流计算模块

将SRM第k相电压平衡方程变形得：

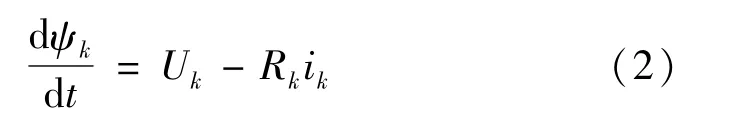
两边同时积分得这一时刻的磁链ψk，再根据转子位置角计算模块计算转子当前位置θk，查表ITBL，得此时的相电流ik。

3.4 转矩计算模块

由转子位置角计算模块得转子当前位置θk，结合相电流ik，查表TTBL，得到此时的电磁转矩Tk，最后将三相电磁转矩分别求和，得SRM总的电磁转矩Te。

3.5 表ITBL、TTBL

表ITBL、TTBL 是所建立SRM 非线性模型的关键，通过以下方式获得。首先，从Ansoft Maxwell 2D导出磁链曲线数据data（电流-角度-磁链）和电磁转矩数据data1（角度-电流-电磁转矩）；然后，通过Matlab 插值后得TIBL（角度-磁链-电流）和ITTBL（角度-电流-电磁转矩）。

4 基于Matlab／Simulink的SRD建模与仿真

建立好了SRM的非线性模型后，低速采用定角度+电压PWM控制；高速采用变角度+电压PWM控制的分段控制策略，并在整个过程对电流进行限幅。最后在Matlab／Simulink里建立三相12／8 SRD的非线性仿真模型。

4.1 SRD仿真总体结构及主要构成

SRD仿真总体结构如图5 所示，由转速给定、转速PI调节、功率变换器、PWM 波产生、角度查询、角度控制、SRM和电流限幅控制等模块组成。

图5 SRD仿真总体结构

（1）转速给定模块。为了模拟SRM 加速减速过程，设置转速先上升至1 500 r／min，再降为500 r／min，最后再上升为1 500 r／min。

（2）转速PI调节模块。转速PI调节采用遇限削弱积分法来实现。其中，比例系数P及积分常数TI通过手动整定得到。

（3）PWM 波产生模块。PWM 波产生模块采用Matlab／Simulink里Repeating Sequence模块来实现的。通过设定Time value和Output value，即可以模拟PWM波。转速经PI调节器输出与Repeating Sequence 模块经比较操作，得到频率为5 kHz，脉宽可调的PWM波。PWM导通脉宽随着电流调节器的输出增大而增大，即占空比提高。正好模拟了DSP控制器，即随着转速PI调节器输出值的增大，比较单元寄存器TxCMPR 的值与周期值TxPR（x＝1，2，3，4）的值越接近，即导通脉宽增加，占空比提高；反之亦然。图6 中设置周期为0.2 ns（频率5 kHz），周期寄存器值为999。

图6 Repeating table设置窗口

（4）功率变换器模块。功率变换器模块如图7（a）所示。输入有电源电压信号、相电流信号以及功率开关管上、下桥臂触发信号。输出为三相电压（Ua、Ub、Uc）。当SRM 某一相导通时，上桥臂（G1、G2、G3）做电压PWM调节，下桥臂（G4、G5、G6）常闭。功率变换器主电路由电流源、续流二极管、IGBT 和电压检测组成，如图7（b）所示。

图7 功率变换器模块组成及其子模块

（5）角度控制模块。角度控制模块如图8 所示。输入有开通角θon、关断角θoff和转子转过的总角度θ（机械角）。输出为角度控制信号（不规则方波），该信号与电压PWM控制输出信号进行逻辑与操作后控制功率变换器的导通和关断，进而控制电动机循环运行。将转子转过的总角度θ 的单位换算为角度（°），然后分别加上0°、30°和15°，得A、B、C三相的相对位置。当此时位置介于θon和θoff之间时输出1；否则为0，最后将两路比较输出经过逻辑与操作，得到在θon和θoff之间为1，其余为0 的三相触发信号sig。

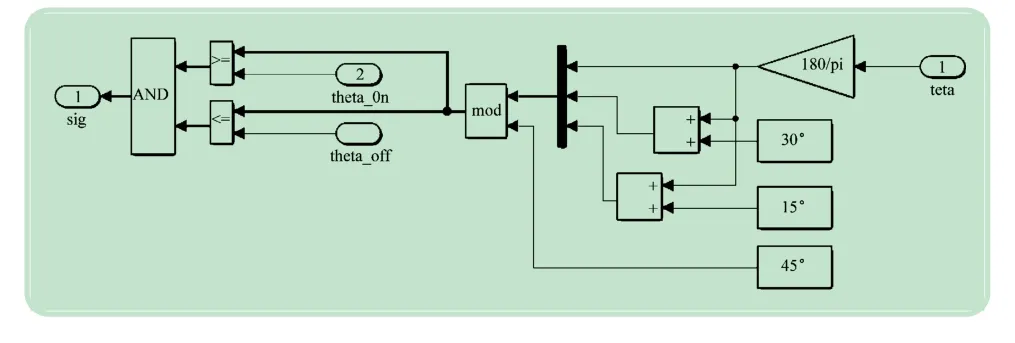
图8 角度控制模块组成

（6）角度查询模块。角度查询模块如图9 所示。当转速≤100 r／min时，设置θon＝2.75°，θoff＝19°，即导通角16.25°；当转速＞100 r／min时，求得，关断角在开通角的基础上加16.25°，即导通角同样是16.25°，即

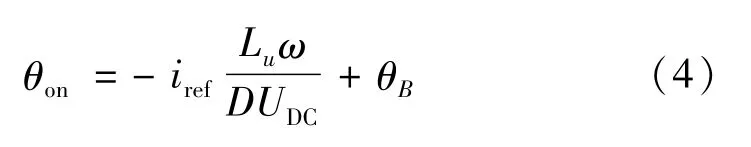
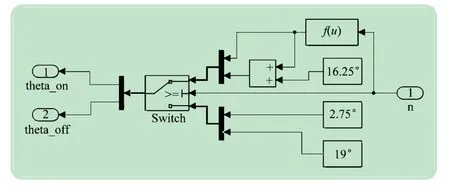
图9 角度查询模块组成

（7）电流限幅控制模块。电流限幅控制模块如图10 所示。当sig为1时，即转子某相绕组导通，此时电流限幅控制起作用，当反馈电流I≥9 A时，电流限幅控制模块输出0，电压PWM 调节失效，所有主开关器件断开；当反馈电流I＜9 A时，电流限幅控制模块输出1，电压PWM 调节有效，即功率变换器上桥臂3 个主开关器件做电压PWM 控制，而下桥臂3 个主开关器件常闭。

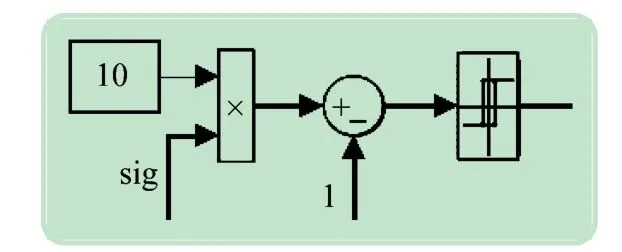
图10 电流限幅控制模块组成

4.2 SRD仿真结果及分析

按照以下控制策略对SRD 进行仿真，即SRD 起动后，当转速低于100 r／min时，采用定角度（开通角2.75°，关断角19°，导通角16.25°）与电压PWM 控制相结合；当转速高于100 r／min时，采用变角度（由式（4）求得开通角，保证导通角16.25°）与电压PWM 控制相结合。系统选用事先计算好的参数：三相12／8 结构SRM，定子相电阻R＝3.5 Ω，电动机系统黏性摩擦因数B＝0.02 N·s／rad，系统转动惯量J＝0.015 kg／m2，额定功率P＝2.2 kW，额定转速Sv＝1 500 r／min，直流电源电压Us＝518 V，θon和θoff的计算详见文献［15］，采样时间Ts＝1 μs。这里取初始化参数：初始角速度ω0＝0 rad／s，初始角度θ0＝0°，各相初始位置角θinitial＝［0 30 15］。

系统带负载起动，负载转矩为9.549 N·m，当转速升至额定转速1 500 r／min时，系统进入稳态运行，在t＝0.35 s时，设置给定转速由1 500 r／min 变为500 r／min，在t＝0.65 s时，设置给定转速有500 r／min 变为1 500 r／min，可得系统0～1 s 的转速波形、0～0.3 s的转矩波形以及SRM A相电流波形分别如图11～13所示。由仿真结果可知：在转速1 500 r／min额定转速下，速度响应快并且很快稳定，SRM 相电流（A相）和电磁转矩波形较为理想，当转速≦1 280 r／min时（t＝0.15 s），电流限幅控制起主导作用（见图13），电压PWM控制失效；当转速＞1 280 r／min时，由于SRM相电流不可能超过其设定上限，此时电压PWM 控制起主导作用。此外，当转速≦100 r／min时，角度控制采用定角度（开通角2.75°，关断角19°，导通角16.25°），当转速＞100 r／min时，角度控制采用变角度（开通角由式（4）求得，保证导通角16.25°）。3 种控制方式有效结合，减小了转矩脉动，使电动机运行更平稳。仿真结果证明了所提出的SRD 建模方法的合理性和有效性［16］。

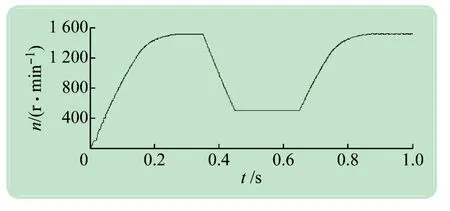
图11 转速响应波形

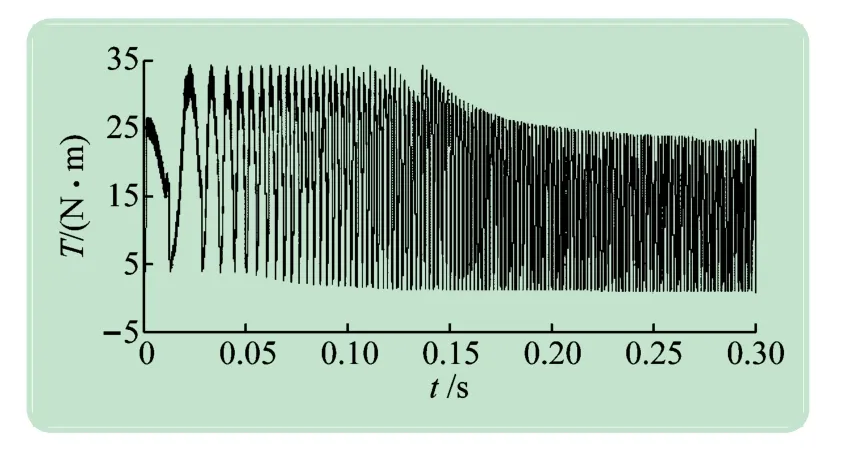
图12 电磁转矩响应波形

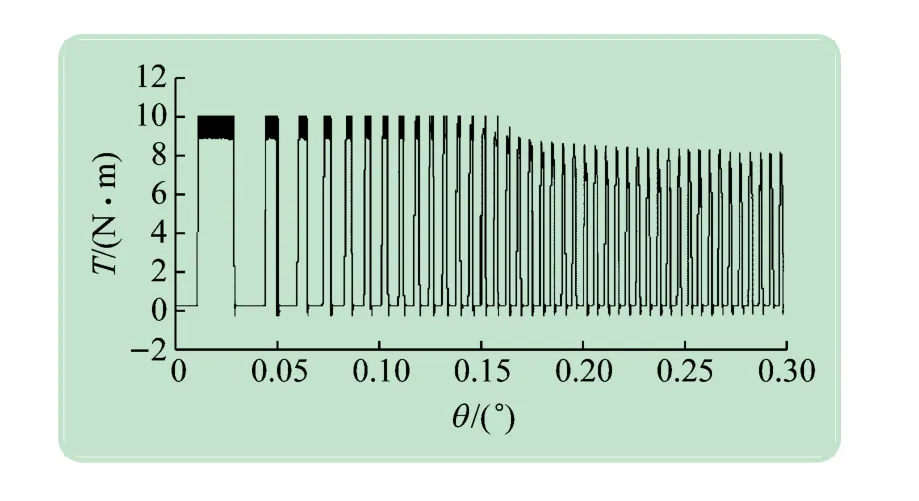
图13 SRMA相电流波形

5 结语

提出了一种基于Ansoft Maxwell 2D和Matlab／Simulink对SRD 进行非线性建模的新方法。通过Ansoft Maxwell 2D对SRM进行有限元分析，得到电动机磁链和电磁转矩数据，将该数据导入Matlab 并进行插值，利用查表的方式建立了SRM的非线性模型。在选定控制策略的基础上，建立了SRD的非线性仿真模型。仿真结果表明：①该模型充分考虑了SRM 的非线性，较准确地反映了SRM磁特性；②所建立的SRD系统采用3 种控制方式（电流限幅、电压PWM和角度控制）相结合，起动时间短，响应速度快，转矩平稳，系统静、动态特性较优。所以，该建模方法为分析和设计SRD提供了有效途径，也为SRD控制算法的设计提供了新思路。