双横臂式独立悬架系统的模态特性分析
陈瑞钦 陈通海 赵 宇 成泰洪
(浙江戈尔德智能悬架股份有限公司,浙江 温州 325000)
汽车是现代生活不可缺少的交通工具,随着社会的不断发展,人们对汽车的操作稳定性与乘坐舒适性的要求也越来越高。悬架系统是汽车不可或缺的总成之一,不仅可以在行车过程中有效地减缓复杂路面所带来的振动和冲击,提高行驶舒适度,还与汽车操纵稳定性紧密相关,汽车的操纵稳定性和安全性在很大程度上由悬架系统的性能参数所决定[1]。
一直以来,有关汽车振动特性的分析是汽车结构设计中非常重要的部分,是在汽车设计过程中必须要考虑到的。国内对于汽车的振动分析研究起步较晚,郭孔辉(1976)在其文章中论述了汽车随机振动,描述了汽车二自由度振动模型在典型实际路面上激起的振动规律,并对试验评价问题进行了讨论[2]。随着技术的积累和科技的发展,如今汽车振动分析在振动理论、数值仿真方法和试验测试技术等方面的研究都已经相对成熟,而模态分析是用来衡量汽车振动特性的重要手段之一。随着计算机技术和有限元分析手段的升级换代,很多学者通过先进的有限元分析方法计算汽车及其零部件的特性。廖权来等(1990)研究了模态分析方法在汽车振动领域的应用[3]。郭跃等(2018)采用模态综合法建立了整车非线性动力学模型,将电动汽车模型划分为转子、定子、副车架、车身子结构及多个连接子结构,获得了各子结构的动力学响应[4]。陈超(2020)以某款汽车座椅骨架为对象,通过多目标优化方法与转角模态识别方法对座椅骨架进行优化设计[5]。Hadad等(2004)在建立了某车架的有限元模型的基础上对该模型进行了模态分析,并根据模态分析结果对该车架的结构进行了优化设计[6]。Anderson等(2007)采用了有限元方法对建立的车架进行了有限元模型的模态分析和随机振动分析,分析了在随机路面激励下该车架的振动响应特性[7]。
本文结合模态分析理论及双横臂式独立悬架系统的结构特点,建立了双横臂式独立悬架系统的有限元分析模型,并通过分析自由状态下悬架系统的模态特性,计算出了自由状态下悬架系统的固有频率和固有阵型。通过考虑悬架系统的负载对模态特性的影响,计算出了悬架系统的频率响应曲线,并分析了负载对频率以及阻尼的影响。
1 模态分析理论
结构的固有频率、振型、振型参与系数和有效质量是结构承受动态载荷设计中的重要参数,通过模态分析可以确定其机械部件的振动特性。结构整体线性化的动力平衡方程如公式(1)。

公式(4)中为固有频率,其值与系统的刚度和质量有关。
2 双横臂式独立悬架系统的有限元模型
双横臂式独立悬架横向刚度大,可以承受较大的侧向力,能精确地设定定位参数,具有抓地性能好、路感清晰等特点。悬架在实际工作过程中本身并不是一个独立的系统,其包括弹性元件、导向装置、减振器、缓冲块、横向稳定器等。图1为本项目中采用的双横臂式独立悬架系统,图2为双横臂式独立悬架系统的有限元模型,其网格数量为264 378个,节点数为490 502个。图3为双横臂式独立悬架系统的边界条件设定,约束条件采用了左右两侧四个点位的固定,在悬置上支架的位置上考虑了负载的加载。

图1 双横臂式独立悬架系统

图2 双横臂式独立悬架系统的有限元模型
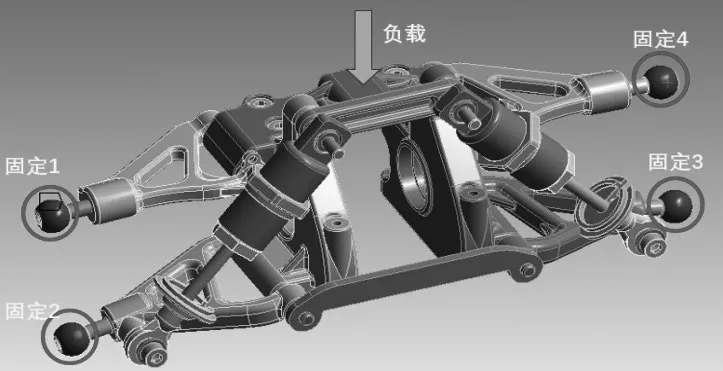
图3 双横臂式独立悬架系统的边界条件设定
3 无负载条件下双横臂式独立悬架系统的模态分析
对于一个复杂的动力学模型,通过建立其数学模型求解模态参数是一个漫长而又复杂的过程。而通过有限元分析方法进行模态分析计算可以较为准确地计算出双横臂式独立悬架系统的固有频率和固有阵型,为后期整车系统的减振和避振提供理论依据。本文首先考虑了无负载条件下双横臂式独立悬架系统的模态特性,经过计算得出其前六阶固有频率分别为78.8 Hz、92.19 Hz、154.1 Hz、172.2 Hz、197.3 Hz、268.1 Hz,对应的固有阵型如图4所示。为验证计算的准确性,在模态分析的基础上进一步计算了系统的频率响应曲线,如图5所示。通过正弦扫频的方式对系统进行激励,从而计算出了在不同频率下其位移的变化特征。从图5中可以看出前六个频响函数对应的峰值正好对应系统的固有频率。每个固有频率所对应的幅值也有所不同,一阶共振频率所对应的幅值最高,其次是二阶固有频率、三阶固有频率、五阶固有频率、四阶固有频率、六阶固有频率。不同频率所对应振幅不同的主要原因如下:

图4 悬架系统的固有阵型

图5 无负载条件下的频率响应曲线
(1)一般情况下随着固有频率阶数的增加频率值会呈现上升趋势,其振动幅度有变小的趋势。
(2)在谐响应分析过程中不同的模态阵型下响应点的位置表现出不同的振动幅度,甚至有些结构点处于零幅度状态。
可以看到在第四阶共振频率下其幅值大小并不明显。因此,在实际做模态振动实验之前,一般可以通过有限元分析的方法对模型的激励点和响应点进行预判。
4 有负载条件下双横臂式独立悬架系统的频率响应分析
悬架系统的作用是传递作用于车架和车轮间的力和力扭,减缓行车过程中复杂路面给车架和车身所带来的冲击,从而减少由此产生的振动,保证汽车的平稳行驶。而车辆在实际行驶过程中悬架系统需要承受不同大小的负载,这对整个系统的模态特性影响是巨大的。表1表示在不同的负载情况下,双横臂式独立悬架系统的固有频率值的变化情况。本分析只截取了影响比较大的前六阶低阶固有频率,针对无负载条件和负载500 kg、1 000 kg、2 000 kg的系统模型进行了比较。从表1中可以看出,每一阶固有频率在负载增加时,固有频率呈下降趋势,这是由于当负载增加时相当于其质量的比重增加,而其刚度变化不大。因为系统的固有频率一般情况下与系统的质量成反比,与其刚度成正比。图6表示在不同负载下悬架系统的频率响应函数的对比图,图中可以明显看出随着负载的增加,固有频率有下降趋势(说明2 000 kg时的第一个增幅点为二阶固有频率)。

表1 悬架系统的固有频率(单位:Hz)
阻尼是机械能在动力学系统中耗散而产生的现象。在利用、分析和测试动力学系统时,对动力学系统中阻尼水平状态的认识很重要,阻尼越大,减震效果会越明显。阻尼一般分为内部阻尼、结构阻尼、流体阻尼等。从图6中可以看出,随着负载的增加,在某种程度上增加了系统的结构阻尼。因此,车辆在实际行驶过程中,负载的增加虽然增加了悬架系统的负荷,可能导致悬架系统的疲劳寿命减小,但另一方面,负载的增加可以增大悬架系统的阻尼特性,在一定范围内有利于车辆的平顺性和稳定性。
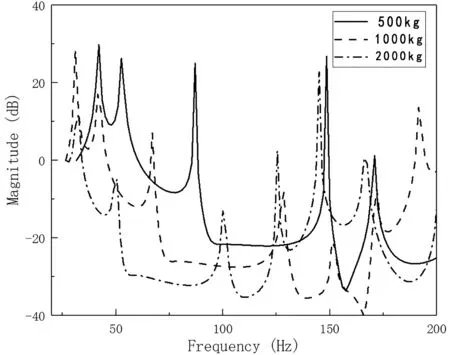
图6 有负载条件下的频率响应曲线
5 结论
双横臂式独立悬架系统具有横向刚度大、可承受侧向力大、定位参数精准、抓地性能好、路感清晰的优点,适用于运动型轿车、超跑、高档SUV、载重商用车轮。本文建立双横臂独立悬架系统的有限元模型,通过模态分析、谐响应分析研究了双横臂独立悬架系统的模态特性。首先,通过计算无负载条件下悬架系统的模态阵型和固有频率,分析了固有频率和阵型的变化特征,为实际的模态振动实验方案提供了理论基础;其次,分析了不同负载条件下悬架系统的模态特性,得出在负载增加时得出固有频率变小,阻尼增大的结论,为悬架系统的设计奠定了理论基础。

