基于性态的液化场地多跨桥梁桩基地震响应分析

惠舒清，唐 亮，凌贤长，，苏 雷，李雪伟，满孝峰

（1.哈尔滨工业大学土木工程学院，哈尔滨，150090；2.青岛理工大学土木工程学院，青岛，266033）

引言

地震是最重要自然灾害之一。地震对桥梁工程等造成的巨大破坏，常常为灾后救援重建工作带来诸多困难。一系列的震害调查显示，强震引发的场地液化诱发桩基础出现塑性铰是导致桥梁破坏的重要原因［1～3］。对于桩基桥梁，地震中液化场地桩上受到的侧向荷载主要有运动荷载和惯性荷载［4～7］。过去发生一系列大地震所造成的重大损失使国内外学者意识到，过去仅以防治结构损伤为目标的抗震设计是远远不够的［8～13］。基于此，美国学者针对结构工程，率先引入基于性态的抗震设计思路（Performance-based Seismic Design），根据设防水准划分不同的抗震性态等级，结合结构使用功能实际情况，合理地确定抗震性态的设计目标并给出合适的结构抗震措施。

目前，围绕桥梁结构的基于性态的地震工程设计中，许多研究者开展了相关研究工作。KRAMER［14］全面回顾了基于性态的地震工程的产生和发展，给出的基于性态设计中常用的基本概念和未来可能遇到的挑战和机遇；SHIN 等［15］基于性态的地震工程研究了液化场地桥梁的抗震特性；类似，KRAMER 等［16］对液化场地桥梁桩基采用基于性态的地震工程方法进行了分析；LEDEZMA 等［17］给出了基于性态的地震工程设计方法，此方法能够很好估计侧向扩流场地桩支结构地震特性；ELGAMAL 等［18］发展了基于性态的桥梁桩基抗震分析计算平台BridgePBEE（https：//peer.berkeley.edu/bridgepbee），该平台可准确考虑桩－土－结构动力相互作用并可以进行整个桩基桥梁结构的性态评估。并基于此平台，考虑耦合的桩－土－桥梁结构体系，采用基于性态的地震工程评估方法研究了典型高架桥梁在不同场地的地震特性；BRADLEY 等［19］等对桩－土－桥梁结构体系进行概率地震响应分析和损失评估。结果表明：非水平的土层结构、场地液化和土－结相互作用显著地影响着桥梁各部分的地震需求特性；MACKIE等［20］在基于性态的地震工程框架内，获得桩基桥梁的优化概率地震需求模型；类似地，SHIN 等［21］建立了液化场地桩基桥梁的数值模型用于评估桥梁地震特性。以上分析可知：基于性态的抗震设计已经在桥梁工程领域得到广泛的应用，如，然而针对液化场地桩基地震响应分析方面应用较少，特别是多跨桥梁结构。鉴于此，本文针对液化场地多跨简支桩基桥梁体系，参考KRAMER 和JALAYER［22］的分析方法，考虑地震随机性的不确定性和认知的不确定性，结合地震危险性曲线自身的不确定性，推导性态指标危险性曲线的解析表达式。在建立的多跨桥梁体系数值模型的基础上，进行大量的数值模拟。根据数值模拟结果，选取地震过程中关键位置的位移和弯矩最大值作为性态指标的响应，通过在双对数坐标下进行线性拟合，得到不同性态指标的地震需求模型和地震危险性曲线，进而分析其响应特性。

1 变量不确定性来源

通常变量的不确定性主要来源两个方面：第一方面是由于认知能力的不足引起的不确定性，主要受当前认知水平的限制；第二方面是由于变量自身的不确定性所致。所以，对于一个特定的变量X，可以采用下面的模型考虑这两类不确定性。

2 基于性态设计方法

一般，基于性态的抗震设计方法，主要采用简化的数值模型来减少计算机时。因为基于性态的设计方法往往要进行大量数值计算，特别是对于岩土工程结构。近年，随着计算机技术的迅速发展和并行技术的日益成熟，基于性态的设计方法得到快速发展，特别是采用有限元方法。基于性态的抗震设计方法主要包括以下步骤：（1）性态指标选取；（2）地震动危险曲线确定；（3）地震动需求模型确定；（4）性态指标危险性曲线确定。以下主要基于上述4个方面展开讨论与分析。

2.1 性态指标的选定

这里选定整个体系的性态指标见图1和表1。这些指标即地震需求变量（Demand Variable，DV）。从表1可见：选取的这些地震需求变量主要分为两类：一类是位移；另一类是弯矩。这两类响应也是工程师在工程设计中最关注的响应。考虑模型上部桥面板刚度很大和模型的对称性。位移响应，主要选取桥台顶、柱墩顶和承台位移及土层分界处桩的位移；弯矩响应，主要选取桥台顶、柱墩顶的弯矩和群桩顶、群桩底和土层分界处桩的弯矩。对于位移和弯矩响应，可以通过建立的数值计算模型，在不同地震动激励下得到，其值实际为其时程响应最大值。

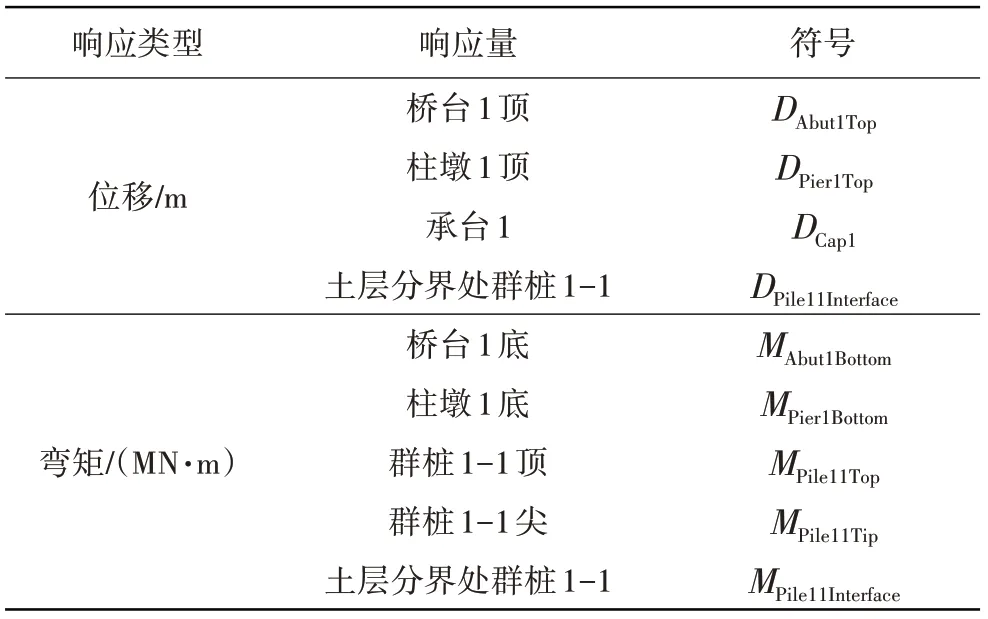
表1 多跨桥梁体系地震需求变量Table 1 Seismic demand variable of multi-span bridge system

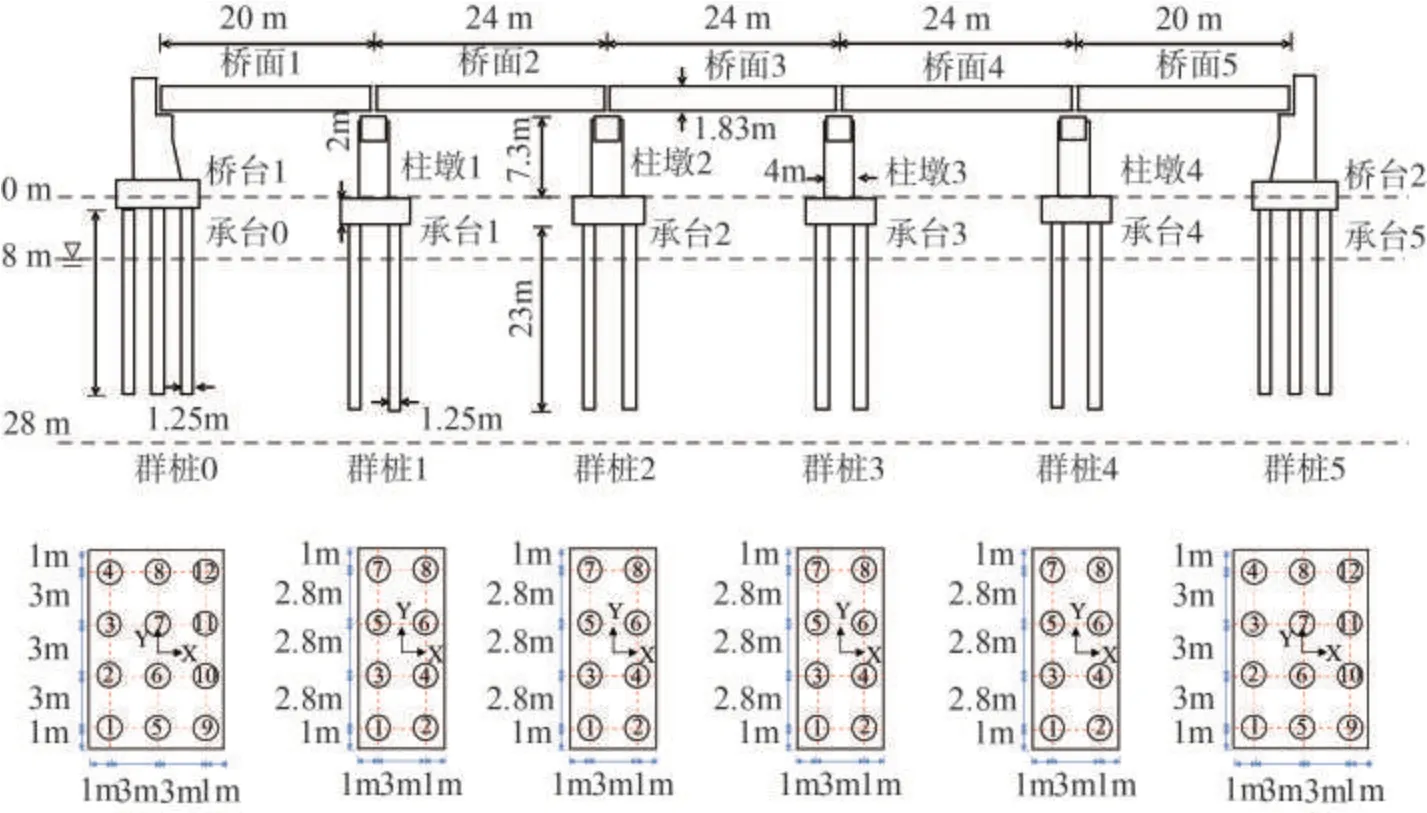
图1 多跨桥梁体系布置示意图Fig.1 Layout of multi-span bridge system

2.2 地震危险性曲线的确定

地震危险性曲线（Seismic Hazard Curve）确定非常复杂。通常，由地震学家通过地震危险性分析得到，地震危险性分析主要针对特定场地的地震动危险性进行定量的评估。KRAMER［23］详细给出了地震危险性分析的步骤。美国部分场地可以从USGS（http：//www.usgs.gov/）得到相应的场地地震危险性曲线。下面结合我国《建筑抗震设计规范》（GB50011-2010），参考前期研究成果［24］，得到以PGV/PGA（为了方便表示，本文采用R表示PGV/PGA）为强度指标的地震危险性曲线，其中：PGA 为峰值地面加速度（Peak Ground Acceleration），PGV 为峰值地面速度（Peak Ground Velocity）。

通常，需要通过地震危险性分析，确定出特定地区的地震危险性曲线。这里仅根据不同设计基准期对应不同烈度值得到对应的峰值速度和峰值加速度的比值R，进而通过R与年平均超越概率进行拟合。通常，近似认为某地区的地震危险性曲线为指数形式分布［25］。正常情况下，危险性曲线需根据场地条件、断层条件且通过地震危险性分析进行确定，然而在进行地震危险性分析时仍进行大量的假设。下面考虑以R表示的危险性曲线的不确定性。若采用相同的指数形式的表达式作为不确定性危险性曲线的中位数的估计，并引入随机变量εUH代表危险性曲线的不确定性，并假定εUH服从对数正态分布。由于地震危险性曲线HR(x)本身为随机变量，所以HR(x)可以表示其自身的中位数与随机变量εU的乘积，所以，HR(x)的平均值-HR(x)可以表示为：

2.3 地震动强度指标与性态指标之间经验关系

为了确定地震动指标（R）与性态指标（如，Dhead）之间的关系，需要输入不同的地震动，进行相应动力时程响应分析，得到性态指标的响应。所确定的这种关系称为地震需求模型（Seismic Demand Model，SDM），通过地震需求模型，给定地震动强度指标值的情况下，近似估计性态指标的值。然而，对于相同幅值的地震动，性态指标的响应存在一定差异性。假定这种差异性主要由于地震动的随机性导致。所以，这里引入R与性态指标中位数的函数关系式，并考虑性态指标中位数由于地震动随机性引起的差异性，引入随机变量εRD解释这种差异性。为了简化分析，采用类似地震危险性曲线的指数形式拟合R值与性态指标DV中位数关系。进一步，由于性态指标的中位数也具有不确定性，这种不确定性主要是由于认知的不确定引起，比如数值模型不确定性、模型参数的精确性等。为了考虑这种认知的不确定性，性态指标DV中位数可以表达为其中位数的估计值与认知不确定性离散变量εUD的乘积，可以得到：

假定εUD和εRD是相互独立的，且服从对数正态分布，这里，μDV(x)称为在给定R值下，性态指标的中位数的值，也记为μDV|R(x)。

2.4 性态指标危险性曲线的确定

首先，只考虑性态指标的中位数由地震动随机性引起的差异性，可以得到：

因为假定随机变量εRD服从对数正态分布，可以得到性态指标DV也是服从对数正态分布的随机变量。

进一步假定在给定R值情况下，性态指标DV的条件中位数近似用指数函数关系进行表述，然而性态指标DV自然对数的条件标准差σlnDV|R(x)是常数。

性态指标DV为不同地震动输入下计算的性态指标的最大值响应。类似于地震危险性曲线，性态指标的危险性曲线定义为性态指标DV超过特定需求值dv的年平均概率，利用全概率公式，分解给定R情况下，性态指标DV超过特定需求值dv的概率和R等于特定值x发生的概率，然后对不同R值求和，引入R的概率密度函数fR（x）与互补累积分布函数G（x）。注意到：（1）地震危险性曲线HR（x）等于R 的互补累积分布函数GR（x）与地震年平均发生率ν 的乘积；（2）性态指标DV也服从对数正态分布，即lnDV服从正态分布；（3）随机变量的对数的平均值等于平均值的对数。采用分部法进行积分，并考虑在地震危险性曲线的不确定性εUH和性态指标认知的不确定性εUD，推导得：考虑由于地震的随机性引起的不确定性和认知的不确定，同时考虑地震危险性曲线的不确定，式（5）即为性态指标的危险性曲线的最终解析表达式。详细的推导过程请参见文献［22，23，26］。

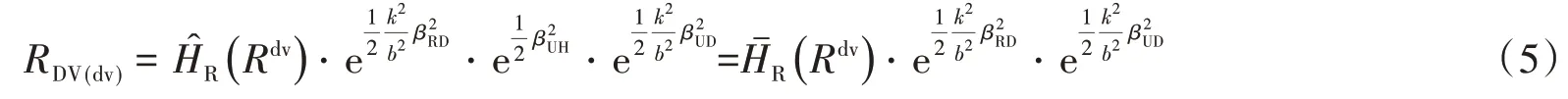
2.5 地震动的选取

基于上述分析，这里选取不同地震动作为基底输入激励，这些地震动的R的变化范围从2.26 s到43.3 s，如图2所示。

图2 选取地震动PGV/PGA分布Fig.2 PGV/PGA value distribution of selected ground motion

3 采用的简支梁桥及简化数值模型

3.1 简支梁桥简介

基于图1-2，借助MssSRA 数值计算平台，建立多跨桥梁体系有限元数值计算模型。以某铁路钢筋混凝土五跨简支梁桥为工程背景。桥梁总长度为112.0 m，五跨主要分成两类，中间三跨具有相同的长度24.0 m，左右两侧跨跨径为20.0 m。针对于桥面板，全部处于同一个平面上。桥墩则采用高度为7.3 m的单圆柱截面实心墩。桥墩截面采用截面直径为4.0 m的等截面形式。桥台采用重力式桥台，桥台宽度为8.2 m，上部背墙高度为1.83 m，下部承重墙高度为8.02 m，翼墙宽度3.965 m。等腰梯形截面的路堤与桥台连接，沿桥纵向和竖向之比为其坡度为0.5，土质为回填砂土，密度为1 987.0 kg/m3，剪切波速492.0 m/s。承台高度为2.0 m，桥台和桥墩下布置钢筋混凝土桩，桩径为1.25 m，桩长为23.0 m。地基分为为两层不同土，上层为松砂层（厚8 m），下层为密砂层（厚15 m）。地下水位线在地表处，上层土属可液化土层。

3.2 简化数值模型

针对上述梁桥结构，为了减小计算量，采用简化的计算模型，土体和上部结构单元并没有采用实体单元，如图3 所示。通过将自由场土体的分析，将自由场地土体位移和孔压作为外部激励，将其输入模拟桩－土界面的p-y宏单元［4］。

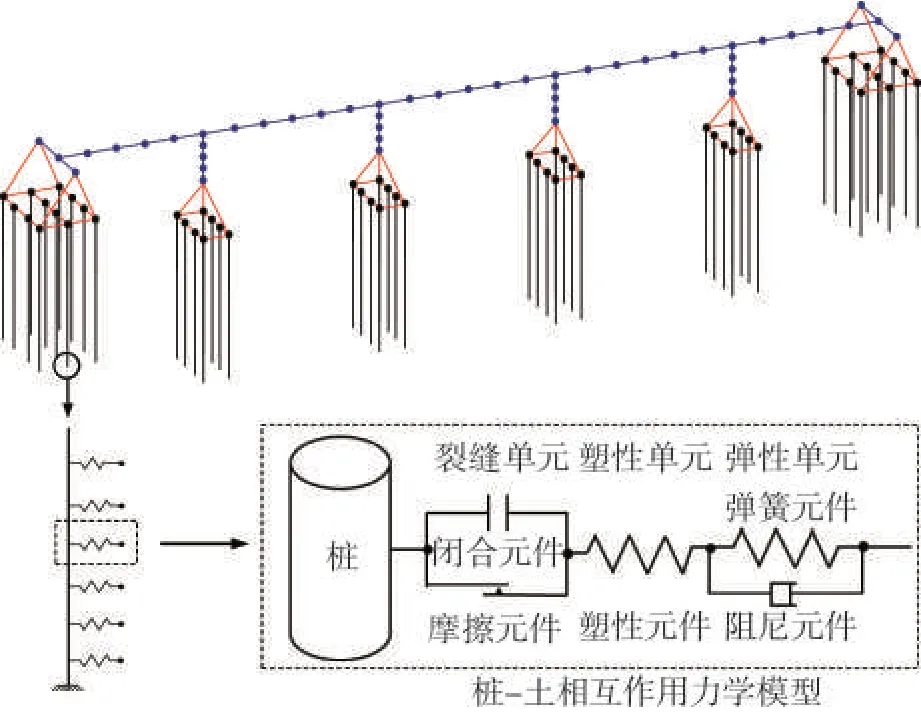
图3 桩-土－桥梁结构体系三维有限元模型Fig.3 Three-dimensional finite element model of pile-soil-bridge structure system

其中：桩－土相互作用力学模型将弹性单元、塑性单元和裂缝单元串联。其中：将弹性弹簧和远场阻尼器并联，能够确保动力相互作用过程中辐射阻尼的作用；裂缝单元以双线性的闭合形式弹簧和非线性物理模型摇曳弹簧组成，以模拟接触-分离的实际作用过程。塑性单元采用“p-乘因子法”修正的砂土p-y曲线描述桩－土地震相互作用过程。这里，将其p-y曲线替换为考虑桩间距效应的液化场地桩－土地震相互作用p-y曲线［26］。桥台采用AVIRAM 等［27］根据Caltrans 抗震设计规范（SDC2004）利用OpenSees 计算平台调整修正得到的简化模型。简支跨中墩顶和桥面连接采用两个零长度单元弹簧分别模拟纵向活动支座和固定支座。由简支梁基本理论可知：相邻桥面板之间在节点处允许发生相对转动。因此，以弹簧描述相邻桥面板直接的连接方式，绑定相邻桥面板3 各方向的平动自由度，释放其转动自由度，允许相邻面板之间发生相对转动。地震作用下，由于桥面板（主梁）的应力主要保持在弹性阶段，且地震破坏时主要集中在桥墩和桩上。因此，桥面板采用刚度较大的线弹性梁单元模拟。分析中，承台不易破坏，而且不满足梁柱的平截面假定，其力学特性近似于刚体，因此采用抗弯刚度和抗压刚度极大的线弹性梁单元模拟。

此外，选取了与本文模型基本相似的唐贞云等［28］在北工大开展的多跨桥梁试验进行了验证，通过Pushover 静力分析法，发现桥墩杆端剪力以及弯矩分布规律均与试验吻合较好，可知该简化数值模型的适用性较好，详见文献［26］。

4 数值计算结果

通过对建立的多跨桥梁体系施加不同幅值的地震动，得到其不同性态指标（即体系关键位置的位移和弯矩地震响应）的地震响应时程，进而得到性态指标响应的最大值，通过双对数的线性拟合，得到性态指标随R 变化关系，即地震动强度指标与性态指标的关系（IM-DV 关系，地震需求模型），进一步考虑地震随机性的不确定性和地震危险性曲线的不确定性，得到性态指标危险性曲线，见式（5）。

4.1 多跨桩基桥梁体系位移响应

图4给出了桥台、柱墩和承台位移地震需求模型和危险性曲线，即性态指标与R关系和性态指标超越特定值的年平均超越概率。图4中的a和b为将R和性态指标在双对数线性拟合时确定的系数，而σ代表性态指标对数值的标准差。从图4中不难看出：整体上位移随着R的增大而增大，但是最大位移并没有出现在最大的R处。利用拟合得到的系数a和b，进一步结合式（5），可以得到不同性态指标年平均超越概率。由图4（a）可知：对于桥台1顶的位移，随着位移增加，年平均超越概率将变小。图4（b）给出柱墩顶的位移地震需求模型和危险性曲线。与桥台顶位移相比，柱礅顶的位移变化规律类似桥台顶，但是相同位移下，其年平均超越概率要更大。表明达到相同位移情况下，柱墩顶年平均超越概率要大于桥台顶，柱墩顶可能更容易出现破坏。图4（c）给出了承台1位移的地震需求模型和危险性曲线。整体上，承台位移随着R的增加在增大，其最大R并没有对应地发生最大位移。其年平均超越概率随着位移的增加而减小。

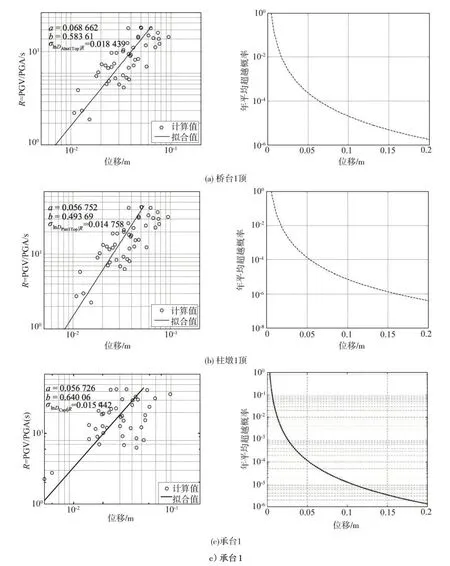
图4 桥台、柱墩和承台位移地震需求模型和危险性曲线Fig.4 Seismic demand model and hazard curve of displacement on abutment，pier and pile cap

考虑到在历次震害调查表明：在土层分界处，由于土体刚度的突变，往往会出现位移的突变，所以这里选用土层分界处桩的位移进行分析。图5 显示在土层分界处桩位移的地震需求模型和危险性曲线。整体上，桩的位移随着R的增加而增大，其最大R几乎对应着桩最大位移的产生。桩位移的年平均超越概率随着位移的增加而减小。从计算结果可以看出：桥台、柱墩和承台的位移范围均处于0.01～0.1 m范围内，而桩的位移则集中于0.001～0.01 m，以R 等于10 为例，柱墩位移为0.024 m，桩基位移为0.004 m，柱墩位移是桩基位移的6 倍。柱墩位移和桩基位移均为0.1 m 时，柱墩对应的年平均超越概率（1.4×10－4）大于桩基对应的年平均超越概率（1.2×10-5）。

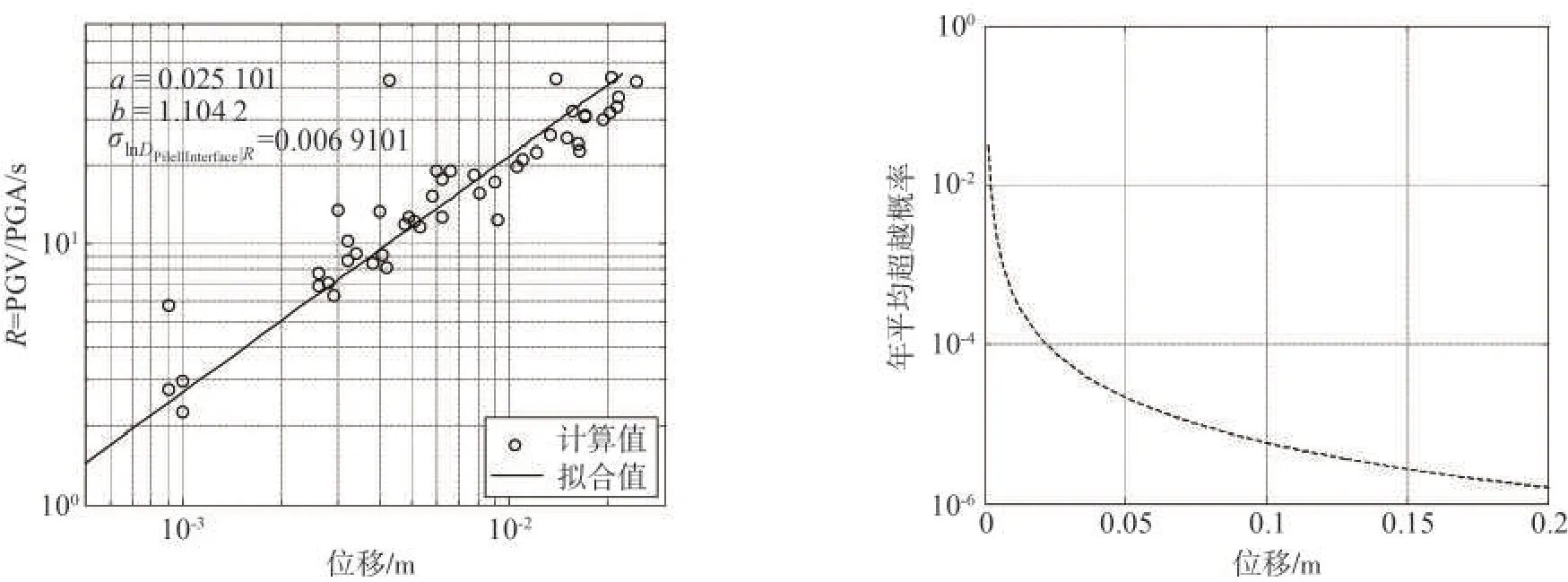
图5 土层分界处群桩1-1位移地震需求模型和危险性曲线Fig.5 Seismic demand model and hazard curve of displacement on the No.1 of pile group 1 in the soil interface

从分析不难看出，整体上，相同R情况下，承台、桥台和柱墩的位移要大于桩的位移，其对应的年平均超越概率也较大。

4.2 多跨桩基桥梁体系弯矩响应

以下讨论体系弯矩的地震需求模型和性态指标的危险性曲线。图6（a）和（b）表示了桥台1 底和柱墩1底的弯矩地震需求模型和危险性曲线。整体上，桥台底和柱墩底的弯矩随着R的增加而增大。同样，其最大R并不对应着最大弯矩。类似地，桥台底和柱墩底的年平均超越概率随着弯矩的增加而减小。对比桥台底与柱墩底弯矩的危险性曲线，不难发现，在相同弯矩下，柱墩底的年平均超越概率要大于桥台底，即柱墩底更容易发生破坏。

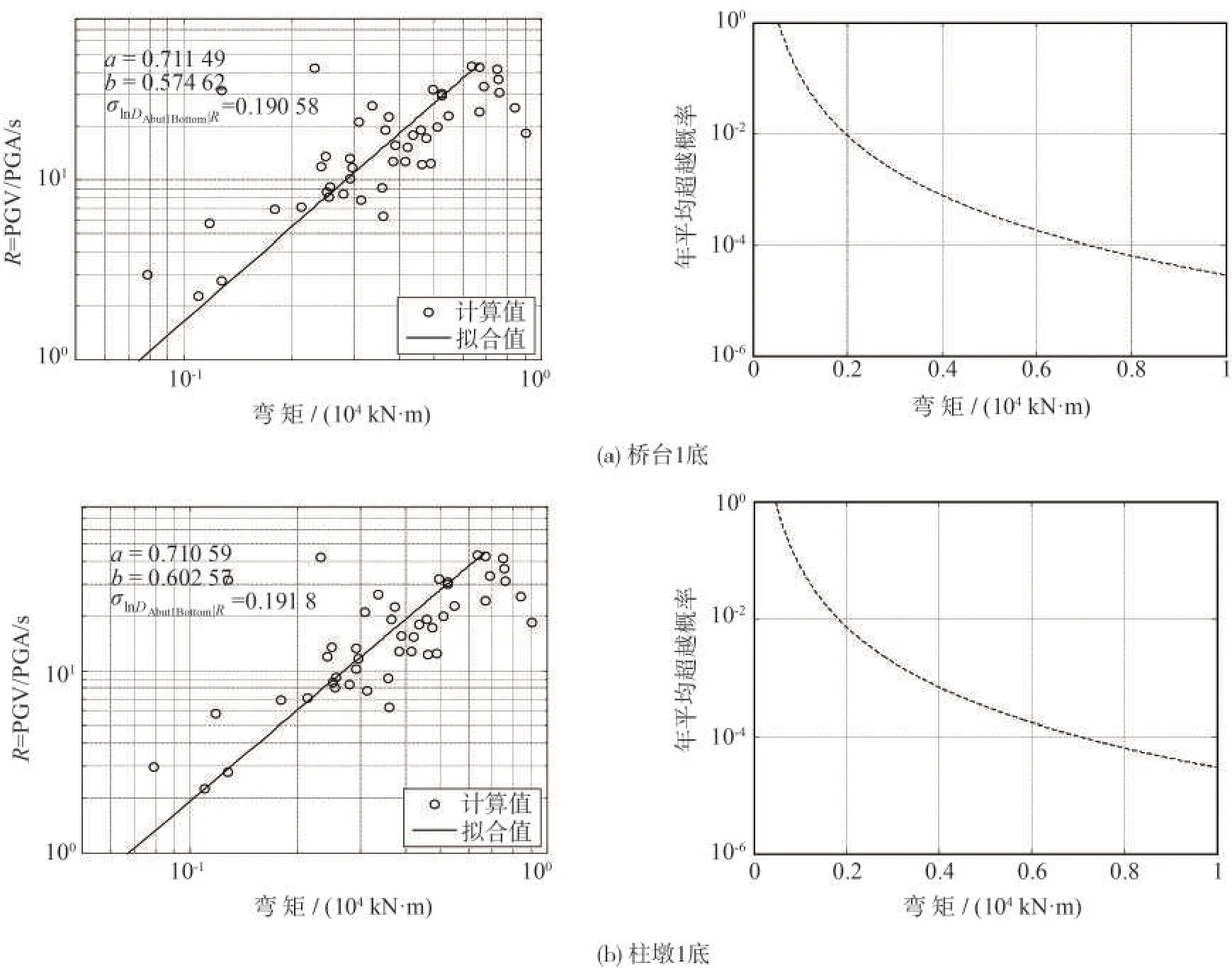
图6 桥台、柱墩弯矩地震需求模型和危险性曲线Fig.6 Seismic demand model and hazard curve of bending moment on abutment and pier

类似于土层分界面桩的位移，图7（a）给出了不同群桩中基桩顶的弯矩地震需求模型和危险性曲线。整体上，基桩顶弯矩随着R的增加而增大，其最大R并不对应着最大弯矩，而年平均超越概率随着弯矩的增加而减小。

图7（b）为群桩不同桩尖的弯矩地震需求模型和危险性曲线。整体上，在双对数坐标系中，桩尖弯矩与R线性拟合较好，即对应的性态指标对数值标准差相对较小。同样、桩尖弯矩随着R的增加而增大，其最大值基本发生在最大R处。年平均超越概率随着弯矩的增加而减小。图7（c）给出在土层分界处基桩的弯矩地震需求模型和危险性曲线。整体上，在土层分界处桩弯矩地震需求模型和危险性曲线与桩尖处类似。

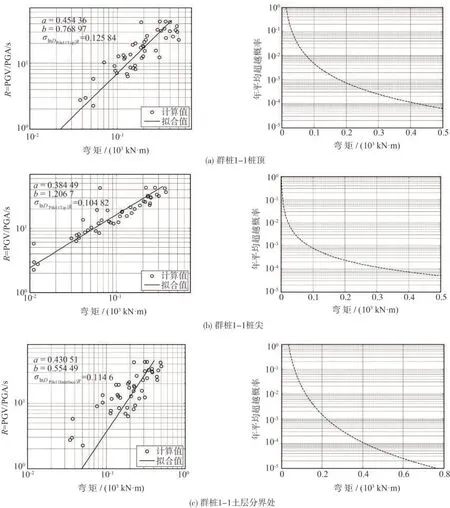
图7 桩弯矩地震需求模型和危险性曲线Fig.7 Seismic demand model and hazard curve of bending moment on pile

综上所述，可以看出：桥台底和柱墩底的最大弯矩基本处于1×103kN·m～1×104kN·m范围内，而桩的弯矩则集中于10 kN·m～1 000 kN·m，以R 等于10 为例，柱墩底弯矩为0.3×104kN·m，土层分界处桩基弯矩为0.167×103 kN·m，二者弯矩相差十几倍。相同R情况下，桥台底和柱墩底的最大弯矩要大于基桩的弯矩，这主要是因为桥台底和柱墩底的弯矩通过承台传至下部群桩。所以，相同弯矩下，桥台底和柱墩底年平均超越概率要更大。

5 结论

本文基于性态设计方法的基础上，考虑变量的两类不确定性，推导了地震危险性曲线、地震需求模型和性态指标危险性曲线，主要结论与认识如下：

（1）基于已建立的多跨桩基桥梁结构体系，拟合得到不同性态指标的地震需求模型和地震危险性曲线，表明采用PGV/PGA作为地震动强度指标可以很好地拟合性态指标，表现出较好的相关性。

（2）基于不同性态指标的地震需求模型，得到体系最大弯矩和最大位移与最大PGV/PGA 并不完全对应。相同PGV/PGA情况下，承台、桥台和柱墩的最大位移要大于桩的最大位移，桥台底和柱墩底的最大弯矩要大于基桩的最大弯矩。

（3）地震危险性曲线本质上是整个结构抗震性能的概率模拟，可以定性得到不同响应量达到或超越某种破坏状态时的年平均超越概率。