基于中美抗震设计规范的双向水平地震效应组合方法的有效性评估

王健泽，戴靠山

（1.四川大学土木工程系，成都 610065；2.中国地震局工程力学研究所地震工程与工程振动重点实验室，哈尔滨 150080）

引言

在现实世界中，当地震来临时，建筑会同时受到多个方向地震波的激励，一般采用两个水平方向分量和一个竖直方向分量来表示［1］。对于竖向地震作用，只对特殊结构形式与体系的抗震设计进行考虑，例如我国《建筑抗震设计规范》（GB50010-2010）［2］要求对8 度与9 度地区的大跨度和长悬臂结构与9 度地区的高层建筑。对于一般规则的建筑结构体系，只需考虑水平地震作用，竖向地震作用由于产生的效应较小常被忽略［3］。振型分解反应谱法与基底剪力法是用于计算单个水平地震作用下结构受到的地震效应，当考虑地震动的两个水平分量同时作用时，需将结构在每个水平方向受到的地震效应按一定规则进行组合。过去已有研究表明了框架结构或支撑框架结构的柱构件需考虑两个水平方向地震作用的必要性。HISADA 等［4］的研究发现：两个水平分量地震动同时作用时框架柱受到的轴向内力在一定情况下是单个水平方向地震效应的2倍；MACRAE 等［5］通过对比双向与单向水平地震动作用下钢框架结构柱的轴向内力与位移响应，也证实了HISADA 等人的观点；ROSENBLUTH 等［6］与WILSON 等［7］先后提出了百分比组合法与平方和开平方根（SRSS）方法，该两种方法也被我国《建筑抗震设计规范》与美国及主流设计规范所采用。两种方法在估计双向地震效应组合的准确性上一直受到关注与研究；王健泽等［8］对比了已有文献对不同双向地震效应组合方法的评估结果，各学者对同一组合方法的有效性仍持有不同的观点。例如，HEREDIA-ZAVONI 等［9］的研究表明百分比规则的估计结果与真实效应值的相对差距最大能达到380%，而REYES-SALAZAR 等［10］研究发现百分比规则的估计结果与真实效应值的相对差距在50%以内。相似的，对于SRSS 的准确性，KHOSHNOUDIAN等［11］认为SRSS方法会低估结构内力响应，而REYES-SALAZAR 等［12］则认为使用SRSS方法既会出现低估也会出现高估结构内力响应的情况，但与真实值的误差均在25%以内。

对不同双向地震效应组合方法的观点相异的现象，也出现在我国《建筑抗震设计规范》与美国ASCE/SEI 7-16［13］在方法选择及结构形式的适用情况的相关规定上。本文将对比我国与美国相关建筑抗震设计规范在考虑双向水平地震效应组合规则上的规定异同，并以三个不同平面布置支撑-框架结构体系作为工程案例，经有限元数值建模与非线性时程动力分析，采用概率性方法评估百分比组合法与SRSS 方法的有效性，并讨论两国建筑抗震设计规范中相关条文的合理性。

1 我国与美国设计规范条文对比

1.1 方法选择

在双向水平地震效应组合方法上，我国《建筑抗震设计规范》（GB50010-2001）版本中对双向地震效应计算规定采用SRSS 方法，并对适用结构范围和构造措施等进行了规定，经姬淑艳等［14］分析发现相关规定条文多是参照国外规范。在《建筑抗震设计规范》（GB50010-2010）版本中，对双向地震组合效应的计算仍要求使用SRSS 方法，而美国ASCE/SEI 7-16 中建议使用百分比组合方法。

以图1 所示的H 型钢柱构件为例，两个水平向地震动分别沿H 型钢截面的强轴X 向与弱轴Y 向输入，得到的内力响应分别用Sx与Sy表示。假定两个水平方向的地震分量之间的强度比值为γ，则SRSS 组合方法可用式（1）表示。在我国抗震设计规范中，γ按0.85进行取值。美国规范建议的百分比规则的公式表达如式（2）所示，百分比规则具体是将结构在任一单向地震作用下结构动力响应的100%与另一正交方向地震作用下结构动力响应的p%进行求和计算。在美国《建筑设计规范》（ASCE/SEI 7-16）中p值取30%。

图1 H型钢柱受双向地震作用下内力效应组合范例Fig.1 An illustration of H-shape column subjected to orthogonal seismic effects

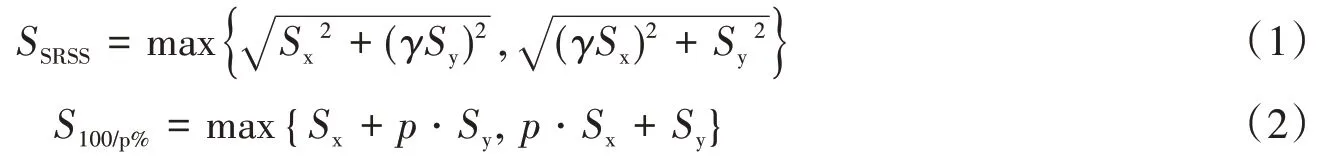
百分比规则也可以看作SRSS 方法的一种特殊情况。现假设在图1 中，X 向地震作用下的响应大于Y 向地震作用下的响应，即Sx＞Sy，且该两个响应值的比值为α，则代入SRSS方法的计算公式（1）后如式（3）所示：

当两个水平向的地震作用之间的比值γ=0.85且α值考虑最不利取值，即α=1时，式（3）则为：

比较式（3）与式（4）可以发现：100/30%规则可以看作SRSS 方法的一种特殊情况，该情况仅在两个水平方向地震作用强度比值为0.85且造成的两个方向的结构内力效应相等时出现。

1.2 适用情况

如上节所述，我国与美国规范分别要求使用SRSS与100/30%百分比简化组合方法以考虑双向水平地震组合效应。同时，在简化组合方法的前提使用条件方面上，两国设计规范的规定也有所差异。对于美国ASCE/SEI 7-16 规范来说，当结构的抗震设计分类属于C、D、E 和F 中任一类且结构体系中出现抗侧力体系斜交不规则时，或者结构的抗震设计分类属于D、E 和F 中任一类且抗侧向力构件同时属于两个或多个水平方向的抗侧力体系时，需采用100/30%百分比简化组合方法对抗侧向力构件进行设计。我国《建筑抗震设计规范》的5.1.1 条规定，对于质量和刚度分布明显不对称的结构，应采用SRSS 方法计入双向水平地震作用下的扭转耦联效应。

基于美国规范的建筑抗震设计，一般是将抗侧力结构体系与抗重力结构体系进行区别设计。举例来说，对于4榀平面框架，可假定2榀框架抵抗该平面内水平地震作用并进行截面设计与验算，其他2榀框架只根据竖向重力荷载组合的最不利效应进行设计。因此，美国规范中会出现抗侧向力同时属于两个或多个水平方向的抗侧力体系。而我国规范是假定全结构参与抵抗地震作用，对于一个空间框架柱来说，是同时属于两个正交平面框架的一部分。后文将通过工程案例更为明晰的说明构件同时属于两个水平方向抗侧力结构体系的情况。

由两国规范对比来看：主要的区别在于美国ASCE/SEI 7-16 不要求平面扭转不规则结构考虑双向水平地震作用，且加拿大《建筑设计规范》（NBCC 2010）中也有同样的要求。更值得注意的是，国际设计规范（IBC）在2003 版到2015 版有很大的变化。在IBC 2003 中要求具有平面扭转不规则或抗侧力体系斜交不规则的结构需考虑双向水平地震作用［15］。但是，到了IBC 2015版本规定地震效应的计算参照美国ASCE/SEI 7的规定，即平面扭转不规则的结构不再需要考虑双向水平地震作用［16］。

2 工程算例

2.1 结构基本信息

本文以一4层中心支撑-框架结构作为工程算例，通过三种设计方案考虑不同的支撑框架布置与扭转不规则情况。该工程案例的平面布置图与立面布置图可见图2-3。对于三个结构方案，在平面布置上，纵向共五跨（X 向），横向共三跨（Z 向），单跨长10 m。在竖向布置上，结构层高4 m，支撑形式均采用人字形。三种设计方案分别代表：（1）平面规则且含双向抗压柱结构（图2（a））。（2）平面不规则且不含双向抗压柱结构（图2（b））。（3）平面不规则且含双向抗压柱结构（图2（c））。为方便后文叙述，三个结构方案依次简称为S4-R、S4-T和S4-TC。这里双向抗压柱具体是指，柱构件是否同时属于X向与Z向支撑框架的一部分。在S4-R与S4-TC 的支撑框架平面布置图中，四个角柱将同时承担X 向与Z 向框架中支撑构件传递的轴向力，而S4-T结构方案中不存在这一情况。

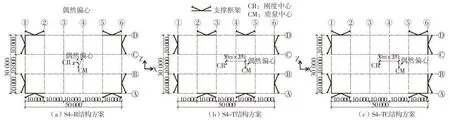
图2 4层中心支撑-框架结构平面图Fig.2 Plan view of the 4-story concentrically braced frame for design schemes

在结构抗震设计上，按美国ASCE/SEI 7-16［13］和《钢结构抗震设计规范》（AISC 341-16）［17］中提供的特殊中心支撑框架体系（Special Concentrically Braced Frames，SCBF）相关要求进行设计。假定水平地震作用仅由所有的支撑框架承担，其他位置的结构构件属于抗竖向力体系。支撑框架布置的位置沿主轴线对称，因此刚度中心在平面的中心位置，结构的质量中心与计入重力荷载代表值的荷载分布有关。对于S4-R 规则结构方案，假定其质量分布均匀并只需考虑偶然偏心的影响。对于S4-T 与S4-TC 两个不规则结构方案，假定质量分布严重不均，质量中心沿X向主轴方向偏心20%造成扭转不规则。S4-T与S4-TC两个设计方案的主要不同为角柱是否同时属于两个正交支撑框架，S4-T 结构的角柱只属于Z 向主轴支撑框架而只承担Z 向水平荷载；S4-TC结构的角柱同时作为两个正交支撑框架的柱构件，将同时承担沿Z向与X向方向水平荷载的共同作用。

综上所述，三种结构方案特点，对照我国与美国抗震设计规范关于双向水平地震效应组合的适用情况规定，S4-R 结构方案为美国规范要求的情况，S4-T 结构方案为我国规范要求的情况，而S4-TC 结构方案同时包括了两国规范要求的情况。

在抗震设计中，假定结构所在位置为地震活跃地区美国洛杉矶（-118.2，34.0），场地条件类型为D 类，反应谱加速度区划值为Ss=2.17 g 和S1=0.79 g。结构重要性分类为II类，抗震设防分类为D 类。设计中，响应调整系数R取6，超强系数Ω0取2，位移放大系数CD取5，重要性系数按1 计算。整个结构的重力荷载代表值为3 011.2 t，计算周期Ta=0.39 s，抗震响应参数Cs=0.34。在构件截面选型上，支撑构件截面选用方钢管，材料屈服强度为345 MPa。柱构件与钢构件截面选用H型钢截面，材料屈服强度为345 MPa。结构构件按S4-R方案进行设计，为了保证三者结构方案的可比性，三个结构方案选用一致的构件截面尺寸，截面标号见表1。

图3 4层中心支撑-框架结构横向（X向）立面图Fig.3 Elevation view of the 4-story concentrically braced frame in X direction

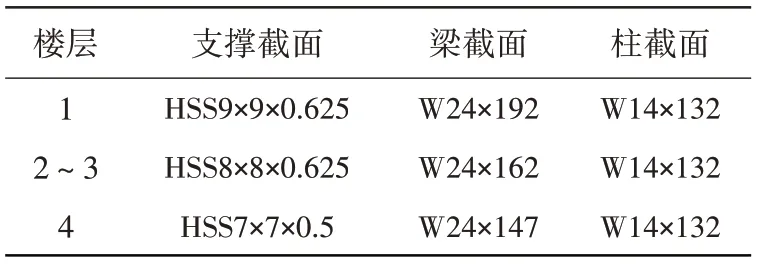
表1 结构构件截面标号Table 1 Information on cross sections of structural components

2.2 地震动选择

地震动输入采用FEMA（P-695）［18］提供的22 组远场地震动，该规程提供22 组地震动旨在通过计算结构抗倒塌性能，以评估与标定抗震设计规范中特定条文与关键参数［19］。所有地震动均是取自较大震级的地震事件，矩震级在6.5到7.5之间。22组地震动样本的加速度反应谱与中位值谱可见图4。因此在本文研究中，利用该22 组地震动对所有结构开展增量动力分析，评估双向水平地震效应组合方法对结构抗震性能的影响。对三个工程算例进行模态分析，得到规则结构方案S4-R 的第一周期（T1）为0.37 s，偏心程度相同的S4-TC 与S4-T 结构具有几乎一致的基本周期，T1=0.39 s。在增量动力分析中，先将22组地震动的加速度中位值反应谱在结构设计第一周期处对应值缩比至罕遇地震反应谱强度，确定缩比系数为Sa(T1,MCE)/S^a(T1,GMs)。在开展的增量动力分析中，将地震动强度增量设为10%Sa（T1，MCE）（0.217 g），增量动力分析中强度变化范围为10%-300%Sa（T1，MCE）。对于每个结构设计方案，在每个地震动强度下开展22 组地震动的双向输入和单向输入下的时程动力分析，共30 个地震动强度，因此每个结构共进行660 次（22×30）双向输入下的时程动力分析，以及1 320次（2×22×30）次单向输入下的时程动力分析。

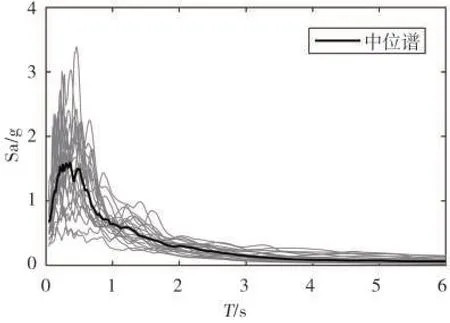
图4 选用的地震动加速度反应谱与中位谱Fig.4 Acceleration spectra of selected ground motions and median spectrum

2.3 有限元建模

三个结构方案采用OpenSees平台建立非线性有限元模型［20］。梁与支撑构件采用基于力法的纤维截面单元模拟。每个支撑构件沿长度分割为8 段，每段设置5 个积分点；梁构件沿长度分割为2 段，每段设置2 个积分点。支撑采用HSS 型截面，按10（长度）×4（厚度）划分纤维；梁构件采用H型钢截面，腹板与上下翼缘均按8（长度）×4（厚度）划分纤维。在后文评估分析内容中主要的考察参数是柱构件的内力响应，为达到理想强度控制构件（force-controlled component）的响应情况，柱构件采用弹性单元模拟，截面强轴方向均沿结构平面Z 向。有限元模型中，采用Steel02 建立材料本构，本构模型参数根据文献［21］的建议取值。同时，为模拟支撑在低周疲劳荷载作用下的断裂，Fatigue 材料模型同时赋予支撑截面的纤维单元。为模拟支撑在受压下的面外屈曲变形，建模中考虑面外缺陷，构件中间节点在面外的偏移距离为自身长度的1/1 000。支撑端部与梁柱节点之间依靠节点板连接，在有限元模型中考虑节点板的面外弯曲塑性变形，通过非线性转动弹簧单元进行模拟。以上建模单元与参数的选取已由文献［21］验证。

2.4 100/30%与SRSS组合规则的概率性评估

（1）评估指标定义

本文提出的概率性评估方法主要目的是评估双向水平地震效应简化组合方法计算支撑框架结构中双向受压柱与扭转不规则结构中柱构件内力响应的可靠性。对于每个结构方案，在每组地震动作用下，要进行三种加载工况：（1）两个水平分量地震动同时激励，分量1沿X向输入且分量2沿Z向输入。（2）地震动分量1沿主轴X向输入。（3）地震动分量2沿主轴Z向输入。

在以上三种加载方式下的时程动力分析中，记录柱构件的最大轴向内力的响应。在一组地震动的双向同时作用下即加载方式（1），柱构件的轴向内力响应采用Pbi-dir表示；采用同一组地震动但只沿X 向与沿Z 向的单向作用下即加载方式（2）与加载方式（3），同一柱构件的轴向内力分别采用Puni-x与Puni-z表示。基于以上所有加载方式下的响应量，提出评估指标Rp，如式（5）与式（6）所示。其中：式（5）用于100/p%组合方法的评估，式（6）用于SRSS组合方法的评估。

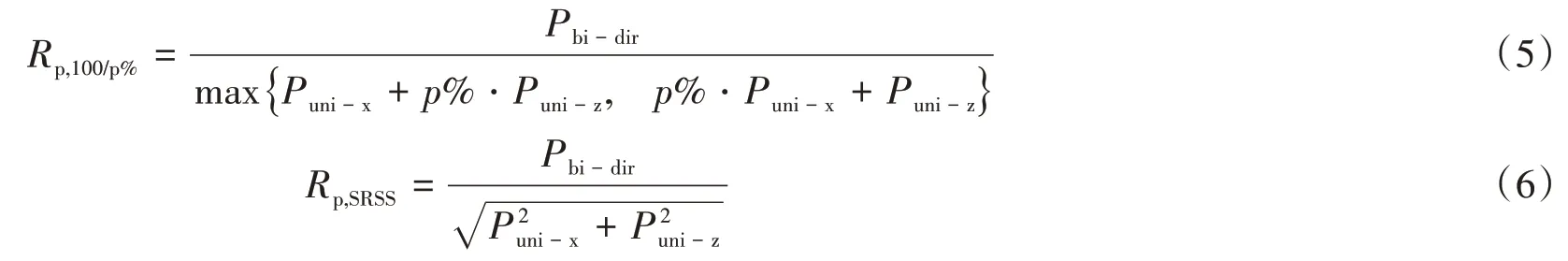
为方便理解，在此列一个实例说明Rp的计算过程。图5 为其中一组地震动作用下时程分析结果中提取的某一柱构件分别在上述三类加载方式下的轴向力响应时程。由图可见：双向加载和两个单向加载作用下，柱受到的最大轴向力的时间不是一致的。提取三个加载方式下的轴向力最大值，代入式（5）与式（6）中，得出Rp，100/30%=1.15，Rp，SRSS=1.09。

双向同时输入下的内力响应可视为最接近现实世界的“真实”值，即是双向地震效应组合方法计算结果的评判基准。因此当评估指标Rp大于1 时，代表100/30%或SRSS 组合规则低估了真实的内力响应，是不安全的；反之，当Rp小于1 时，代表100/30%或SRSS 组合规则的计算结果是保守安全的。在图5 展示出的范例来说，两个评估参数值均大于1，说明100/30%与SRSS方法低估了该柱在双向地震作用下的效应。

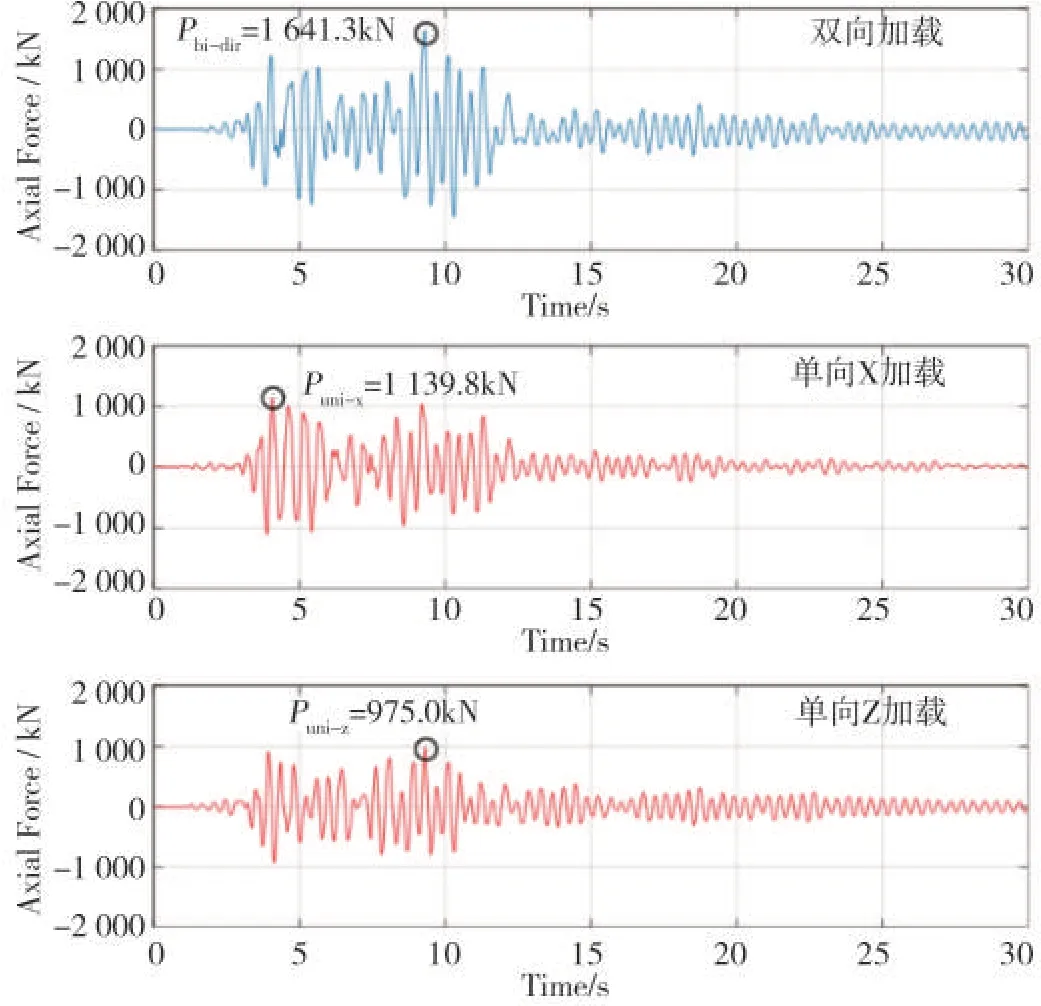
图5 柱构件在三类加载方式下轴向力响应时程Fig 5 Time histories of axial force demand at the column under three different loading cases

（2）评估指标随地震动的分布

基于所有结构方案的增量动力分析结果，计算每个结构所有1层角柱的Rp值并在图6-8中画出Rp值随地震动强度增加的变化趋势。因每层共4 个角柱，选取的地震动共22 组，因此每个地震动强度下共88 个Rp值，每个Rp值采用蓝色空心方框表示，同时每个地震动强度下88个Rp值的中位值用黑色实线在图中画出，16分位值与84 分位值的变化趋势采用黑色虚线表示，16 分位值与84 分位值之间的绝对差值δ（84th-16th）来量化Rp值分布的离散性。地震动强度以结构第一周期下的加速度反应谱值Sa（T1）为衡量参数，变化范围同IDA 分析的考虑范围相同，即10%～300%Sa（T1，MCE），图中横坐标已用Sa（T1，MCE）归一化。

图6 为S4-R 结构的Rp分布结果，在10%～300%Sa（T1，MCE）范围内，Rp，100/30%中位值一直在1.0 上下略微浮动，离散性指标δ（84th-16th）在0.41～0.67范围内变化。就SRSS方法对应的评估指标Rp，SRSS，中位值在考虑的地震强度变化范围内一直稳定在0.96 左右，δ（84th-16th）值在小震强度下约为0.51，当地震强度增长至Sa（T1，MCE）时，δ（84th-16th）值达到0.63，之后逐渐减小至0.38。由此看出，Rp，100/30%和Rp，SRSS的变化趋势基本一致，无论从中位值还是离散性来看，Rp，SRSS的结果比Rp，100/30%略小。

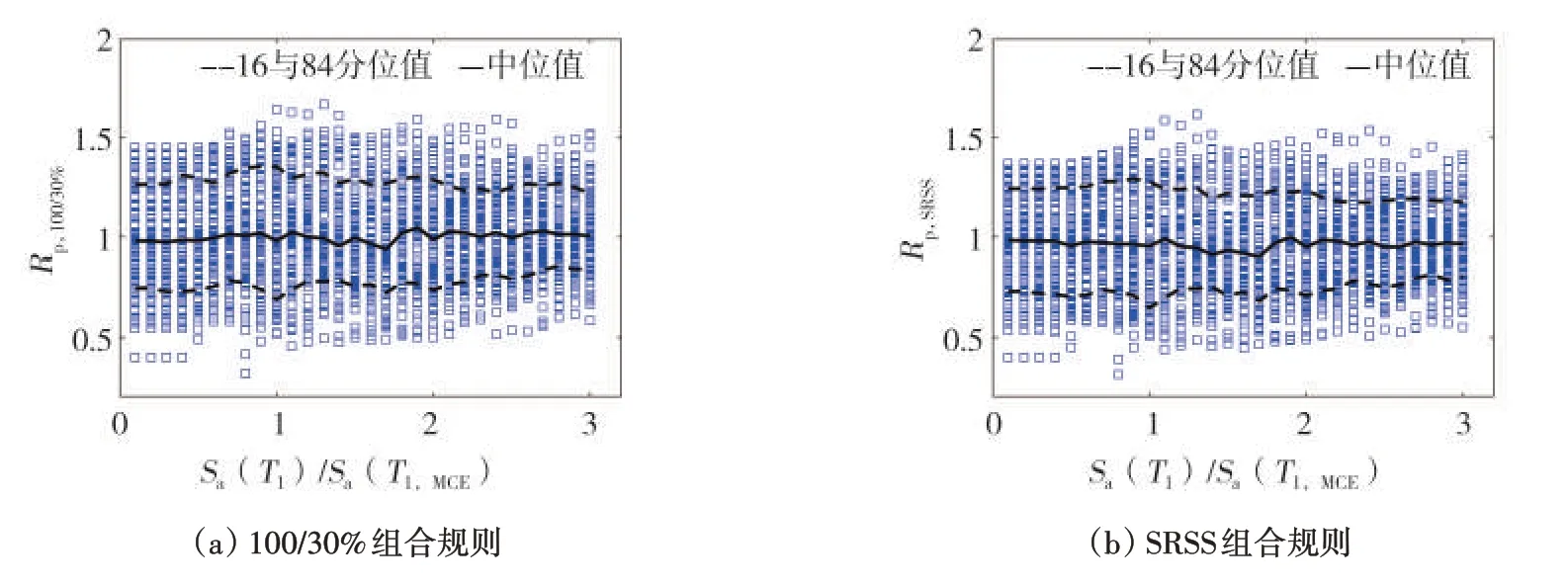
图6 S4-R结构1层角柱Rp值随地震动强度变化的分布Fig.6 Variation in Rp values at 1st story column of S4-R building with increase in seismic intensity

图7 为S4-T 结构的Rp值分布结果。与图6 展示的规则结构的Rp变化趋势不同，Rp，100/30%和Rp，SRSS的中位值、16分位值以及84分位值随地震动强度增加呈现明显下降的趋势。以中位值的变化为例，随着地震动强度增加，Rp，100/30%和Rp，SRSS的中位值从0.98 和1.00 分别下降至0.85 和0.87。与S4-R 结构方案的结果不同的是：S4-T 的Rp离散性量化参数δ（84th-16th）呈上升趋势，在整个地震强度变化范围内，Rp，100/30%的δ（84th-16th）从0.11 上升至0.36，Rp，SRSS的δ（84th-16th）从0.12上升至0.37。

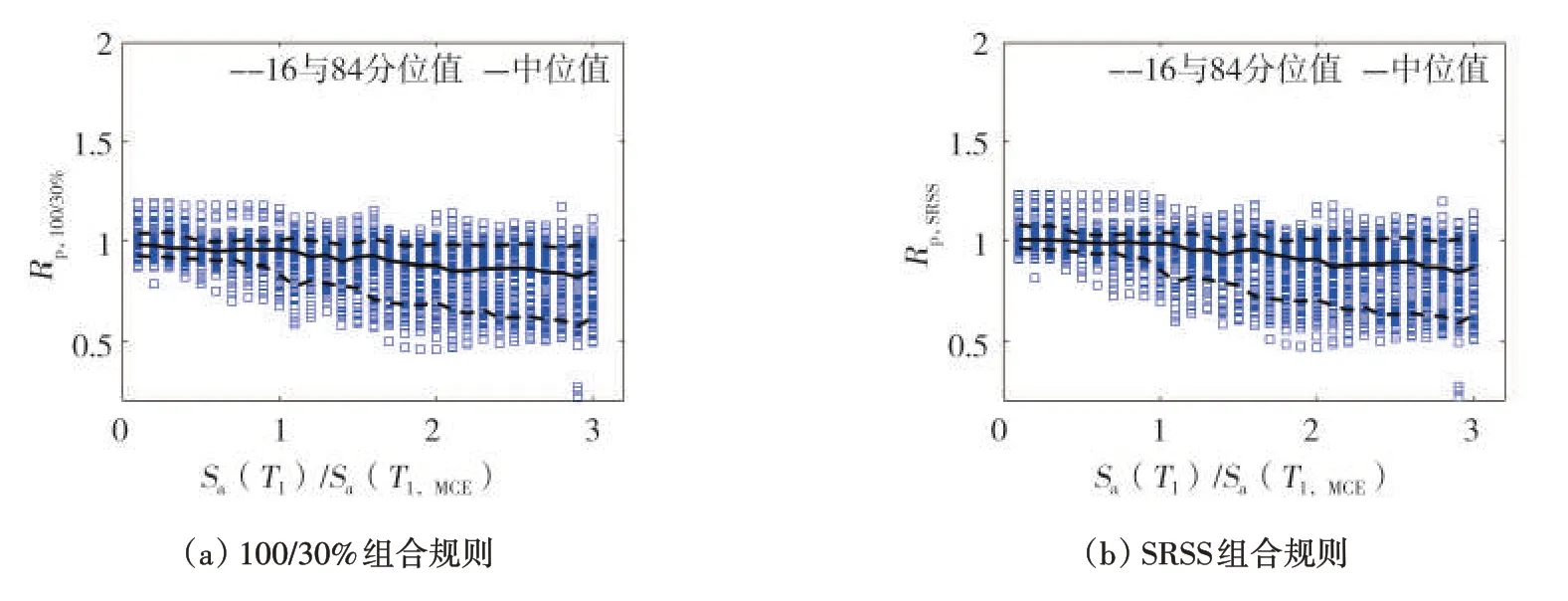
图7 S4-T结构1层角柱Rp值随地震动强度变化的分布Fig.7 The variation in Rp values at 1st story column of S4-T building with increase in seismic intensity

相似的，图8展示了S4-TC结构的1层柱构件的Rp值随地震动强度变化的分布。与S4-T结构相似，两者在平面上属于扭转不规则，角柱构件需抵抗扭转效应。但不同的是：S4-TC结构的角柱同时属于两个正交抗侧力体系的框架柱。从Rp分布结果上来看：与规则结构S4-R 的结果相似。具体来说，Rp，100/30%的中位值在10%～30%Sa（T1，MCE）地震强度作用下稳定在1.02，随后当地震强度增长至180%Sa（T1，MCE）时，Rp，100/30%的中位值减小至0.89，随后在0.89 到0.92 的范围内浮动。Rp，SRSS的中位值在小震强度作用下为1.04，随后当地震强度增长至180%Sa（T1，MCE）时逐渐降低至0.86，在大于180%Sa（T1，MCE）的地震动强度下其中位值在0.86 到0.90 范围内浮动。Rp，100/30%的离散性，即δ（84th-16th）值，在整个10%～300%Sa（T1，MCE）地震强度内变化范围为0.34～0.49；Rp，SRSS的δ（84th-16th）值的变化范围为0.36～0.52。两者的离散性结果与S4-R结构（图6）的结果相近。然而，对于84 分位值，S4-T 与S4-TC 两个结构的结果相差较大，以Sa（T1，MCE）地震强度下的结果为例，S4-T 结构的Rp，100/30%的84分位值为1.25，而S4-TC结构的Rp，100/30%的84分位值为1.04。

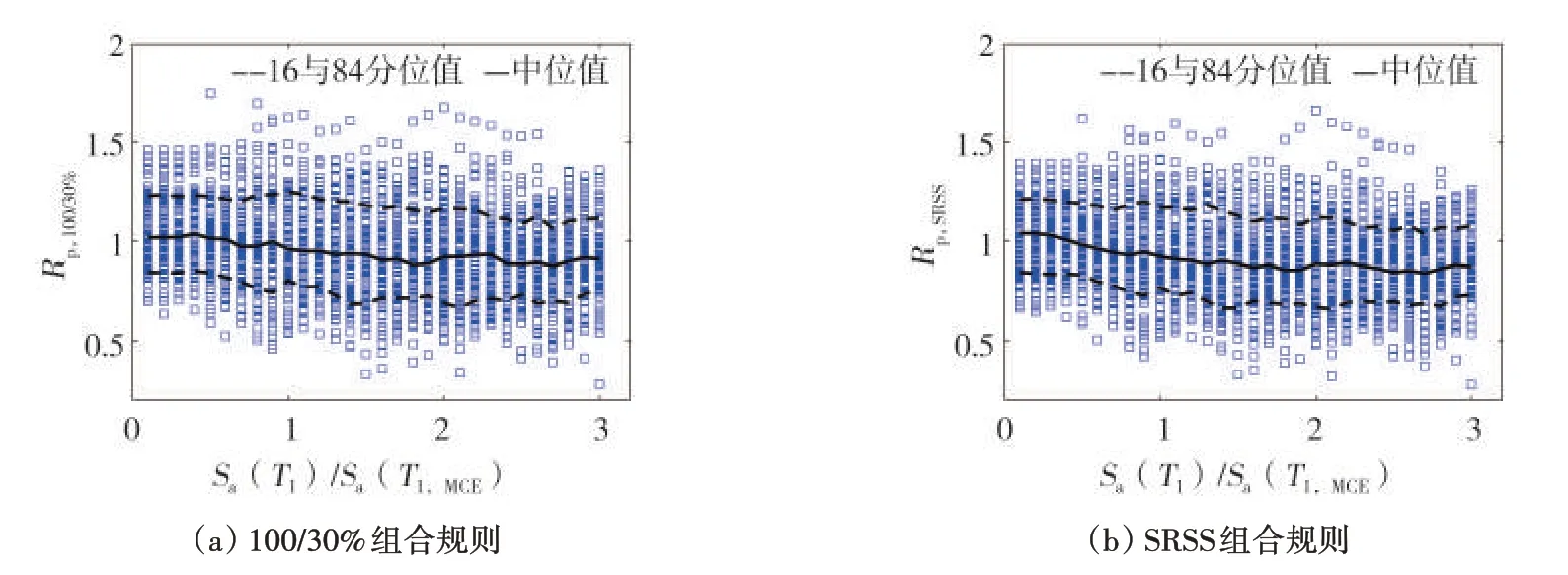
图8 S4-TC结构1层角柱Rp值随地震动强度变化的分布Fig.8 Variation in Rp values at 1st story column of S4-TC building with increase in seismic intensity

从图6-8 中S4-R、S4-T 和S4-TC 结构的结果对比可以看出：同属于两个正交抗侧力体系的柱构件对双向水平地震效应更为敏感，而当柱构件仅抵抗扭转效应时，100/30%和SRSS 方法对内力响应的估计是足够且安全的。

经K-S概率分布检验，验证了图6-8中各结构方案角柱的Rp值服从对数正态分布。需再次说明的是：当Rp值大于1时，说明采用的双向地震效应简化组合方法对结构响应的估计是不足或不安全的。图9对比了4层规则结构S4-R 与两个不规则结构S4-T 与S4-TC 在罕遇地震作用下1 层角柱Rp值的超越概率分布。由S4-R结构（红色实线）和S4-TC结构（黑色虚线）的结果对比可以看出：扭转不规则对双向受压角柱Rp值的超越概率分布影响较小，两者结果分布较为接近，且两个概率分布的中位值（POE=50%时对应的Rp值）基本一致。当对比平面扭转不规则S4-T与平面规则S4-R的结果时，首先可以看出S4-T的Rp值的超越概率分布的标准差较小，换言之，随Rp值增加超越概率减小较快，当Rp，100/30%＞1.07 或Rp，SRSS＞1.11 时，超越概率已降至10%以下。当Rp，100/30%大于0.9 时或Rp，SRSS大于1 时，S4-T 结构的超越概率小于S4-R 的结果。以上对比说明了，平面规则且含有双向受压柱的结构相比平面扭转不规则结构在双向水平地震效应组合上需考虑的更为保守。

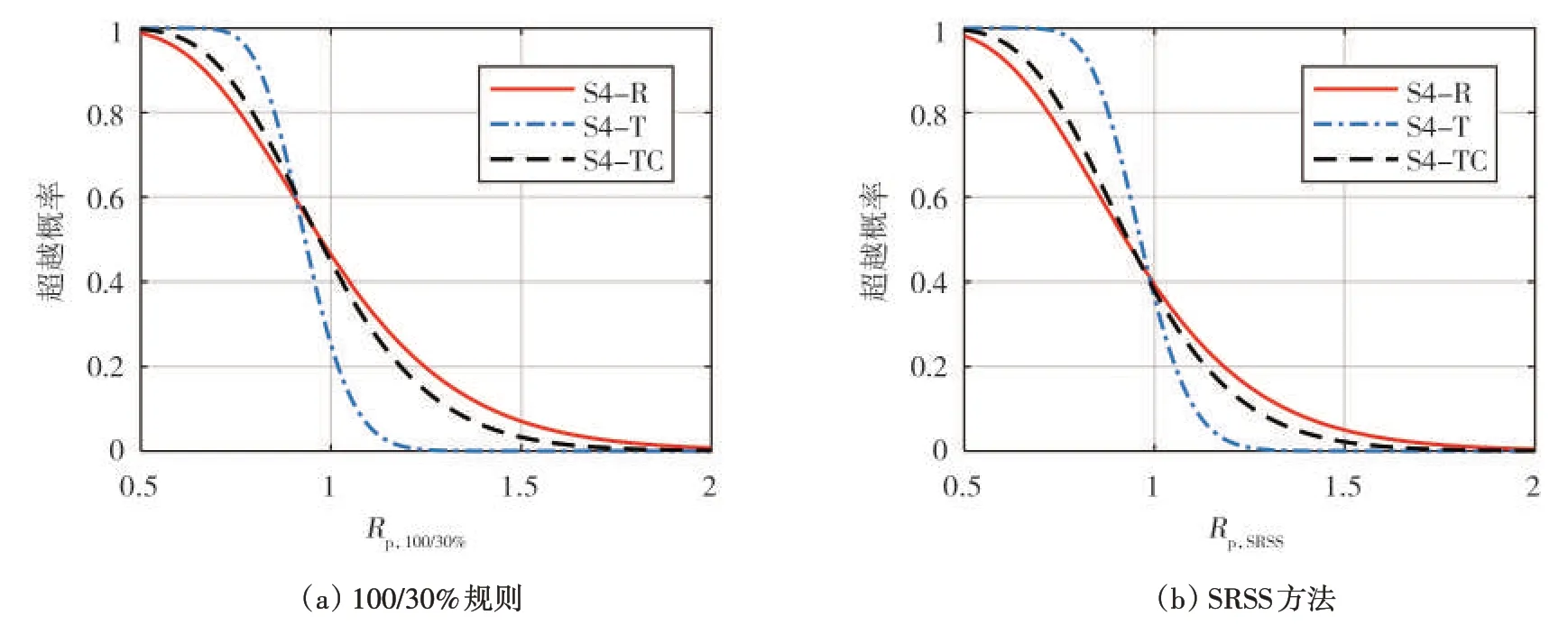
图9 罕遇地震作用下各结构方案1层角柱Rp值的超越概率分布Fig.9 Probability distribution of Rp values under maximum considered earthquake for every design scheme

对于百分比100/p%规则中p值的选取，目前在现行设计规范中主要为30%和40%。在学术界的讨论中，有部分文献基于确定性方法的评估结果给出了百分比参数p不同的建议值。通过计算不同p值下的Rp的超越概率分布，可求出p值与Rp＞1 对应的超越概率之间的关系，可根据工程设计需要，基于超越概率选择合适的p值进行设计。图10 对比了三个结构方案使用百分比100/p%规则在不同p值下发生Rp＞1 的超越概率分布。可以看出含有双向抗压柱的S4-R 与S4-TC 的结果较为相近。对于仅是扭转不规则的S4-T 结构来说，如果发生Rp＞1 的超越概率的允许值为0.5 时，则结构的抗震设计不需要考虑双向地震效应，或使用100/p%规则使结构设计更为安全。当Rp＞1的超越概率的允许值为0.1 时，两个扭转不规则的结构方案相比S4-R规则结构反而需要略小的p值。

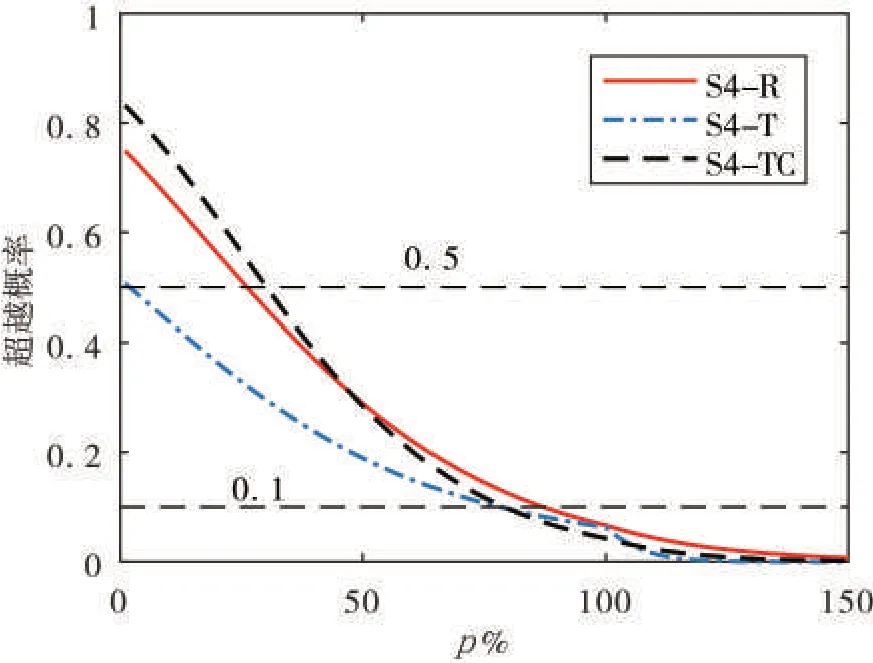
图10 百分比100/p%规则下Rp＞1超越概率与p值关系Fig.10 Relation between probability of exceeding Rp＞1 and the value of p in percentage rules

3 关于我国抗震规范相关条文的讨论

如本文2.2 节中所述，我国《建筑抗震设计规范》中要求扭转不规则结构体系在抗震设计时需考虑双向地震作用的组合效应。本文选取分析的三个结构方案，对SRSS 与100/30%方法的评估结果发现：平面规则结构S4-R 的角柱设计比平面不规则结构S4-TC 与S4-T 更需使用更保守的双向地震效应组合方法，这与我国规范要求相左。

为了讨论支撑-框架结构扭转不规则结构体系是否需要考虑双向水平地震效应组合，图11对比了S4-R与S4-T 结构X 向框架柱内力响应与地震作用强度的关系。注意的是：图11 中给出的是两个结构方案中非双向受压柱的内力响应结果，即仅考虑扭转不规则的影响。图中每条线代表双向加载或单向加载工况下该柱构件内力响应的中位值。由图中可以看出：X 向单向地震作用下的内力响应（红色点划线）与双向地震作用下内力响应（黑色实线）较为接近。而由于S4-T 的扭转效应较大，在Z 向单向地震且强度相同作用下（蓝色点划线），S4-T 的柱构件内力响应比S4-R 的柱构件内力响应要大。因此，S4-T 结构在两个单向加载工况下的内力响应经SRSS 或100/30%方法组合后，比S4-R 结构对应的组合内力响应要大。对于S4-T 结构，单向地震作用下的效应用于设计是充分的，考虑双向水平地震组合效应反而使设计结果更为保守。

为了研究扭转不规则与双向受压柱同时存在的情况，图12 对比了S4-R 与S4-TC 结构的角柱轴向内力响应与地震作用强度的关系。其中：S4-R 结构的结果代表着仅有双向受压柱的情况，S4-TC 结构的结果代表着两个前提条件均存在的情况。由图11可以看出：双向地震作用下的内力响应（黑色实线）大于其他两个单向地震作用下的内力响应结果。因此，对含有双向受压柱的情况，双向水平地震效应组合必须在设计中考虑，任一单向地震作用下的计算结果均无法代表结构在现实中经历地震的“真实”响应。相比S4-R 的结构，S4-TC结构受扭转效应的影响，双向地震作用下内力响应与其他两个单向地震作用下的内力响应之间差距较小，则经双向地震效应组合方法计算后，更易大于双向地震作用下的内力响应，这也印证了图9-10中的结果。

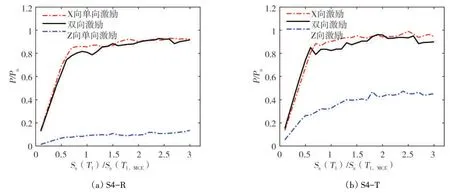
图11 不同加载工况下X向轴线框架柱（非角柱）轴向内力响应随地震作用强度变化Fig.11 Force demands at columns（not at corners）in X-directional frames under different loading cases

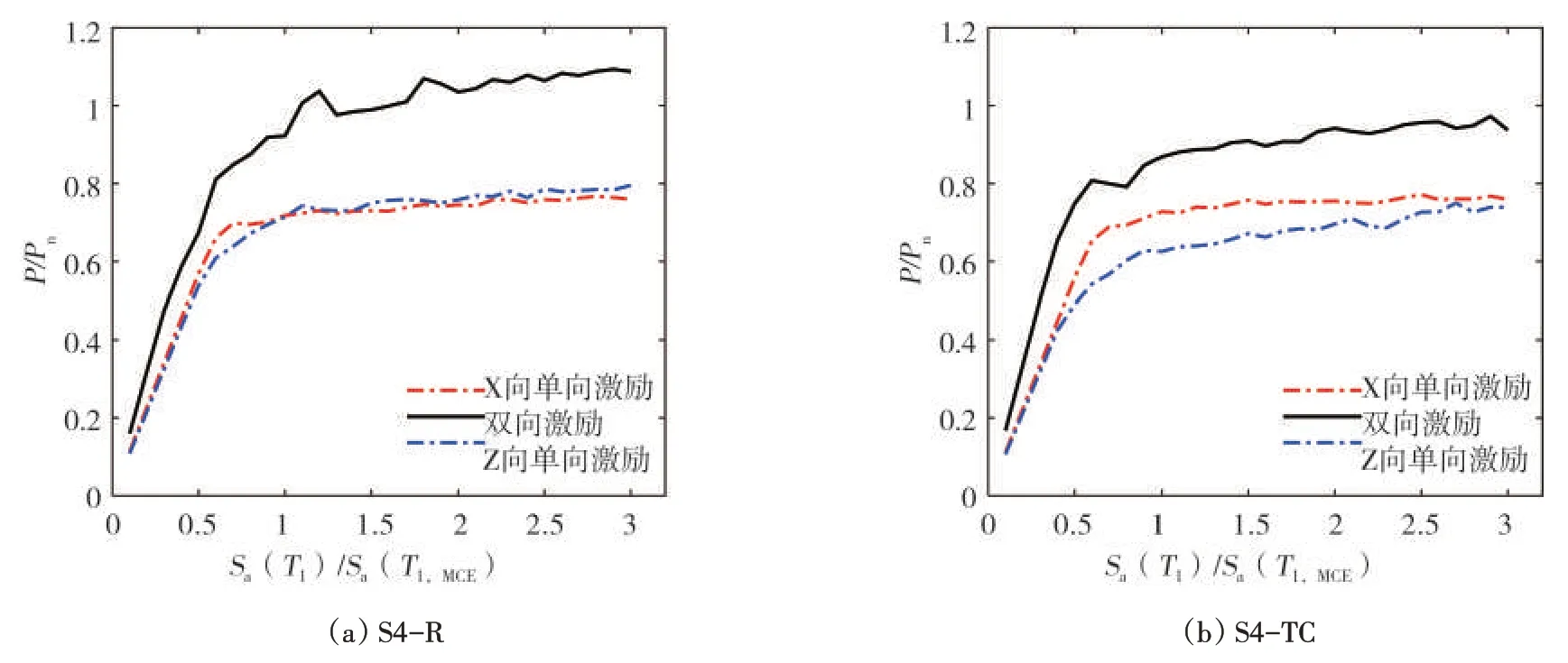
图12 不同加载工况下双向受压角柱轴向内力响应随地震作用强度变化Fig.12 Force demands at corner columns under different loading cases

4 结论

在设计与分析计算中，一般认为建筑结构同时受三个地震分量的同时作用，即两个水平方向分量与一个竖直方向分量。对于两个水平方向地震效应的组合，我国与美国规范在采用的组合规则方法以及适用情况上，均做出了不同的规定。本文采用一4 层中心支撑-框架结构作为工程算例，针对我国与美国规范在设计中考虑双向水平地震效应组合的不同适用情况，设置了三个结构布置方案。通过有限元建模与时程动力分析，采用概率性评估方法，研究了SRSS方法与百分比100/30%方法的有效性，并基于计算结果讨论了我国与美国规范条文的异同。主要得到以下结论：

（1）随地震动强度的增加，规则结构的Rp，100/30%或Rp，SRSS值的中位值有小幅上升趋势，而不规则结构的Rp，100/30%或Rp，SRSS值的中位值呈现下降趋势。因此，当地震动强度增加时，100/30%与SRSS方法对平面规则的中心支撑-框架结构的双向受压柱的响应估计偏不安全，而对扭转不规则结构柱构件的响应计算更为保守。

（2）Rp，100/30%与Rp，SRSS的概率分布结果表明：考虑双向水平地震效应组合的前提条件“构件同属于两个正交方向抗侧力体系”的重要性大于“扭转不规则”。SRSS和100/30%方法用于扭转不规则结构的抗震设计是合理且安全的，且简化组合规则的超越概率容许值为0.5时，可不需考虑双向水平地震效应组合。而中心支撑-框架结构中含双向受压柱时必须考虑双向水平地震效应。

（3）对比我国与美国规范条文与要求，SRSS与100/30%两种方法在组合效应估计时，差距不大。但在简化组合规则的适用条件上，美国规范对平面扭转不规则结构不进行考虑有一定的合理性。同时，建议我国规范对中心支撑-框架结构中含双向受压柱的情况要求考虑双向水平地震效应组合。