圆弧形沉积谷地在平面SV波入射下地震响应的有限元分析

蔡曼琳，丁海平，2，于彦彦

（1.苏州科技大学江苏省结构工程重点实验室，江苏苏州 215011；2.中国地震局工程力学研究所，哈尔滨150080）

引言

地形对地震动的影响研究主要有两种方法：一种是利用场地观测台站的地震记录；另一种是理论分析方法，常用的有解析法和数值法。解析法主要指的是波函数展开法［1－4］，考虑的地形几何形状和介质的材料特性相对比较简单，其结果可以用于检验数值法的计算精度。而数值法的种类较多，文献［5］把数值法归纳为3 类：域方法，包括有限差分法、有限元法和谱单元法［6－11］；边界元方法［12－14］；将几种数值方法相结合的联合方法［15－16］。沉积谷地（盆地）作为最常见的地形之一，是人类生活和工作的主要区域，研究其对地震波的传播影响很重要。对于复杂的地形和地质条件的场地，解析法受到一定的限制。随着计算机的发展和大型有限元软件的出现，有限元数值法已成为一种更方便和更有效的手段。采用有限元方法分析场地效应时，需要用人工边界把半空间问题限制在一个有限的区域内解决。目前的大型有限元软件大多没有设置人工边界，但可以采用基于粘性边界或粘-弹性边界的等效荷载输入方法实现［17－20］，由于在满足这些边界条件时存在参数选择问题，其精度受到一定限制。在众多的人工边界中，多次透射公式（MTF）是一种易于实现且精度较高的局部人工边界条件［21］。本文将利用Ansys 有限元软件结合MTF 的计算工具，分析圆弧形沉积谷地对入射SV 波放大特征。由于场地地表地震动峰值的分布受不同地震波输入的影响，如文献［22］发现：同一个场地模型在不同的地震波入射下，地表的地震动峰值分布呈现显著的差异性；文献［23］也指出：不同地震波作用下，地震动峰值放大系数的影响程度和范围有区别，因此，本文将进行频域结果分析，避免受不同输入地震波的影响［24］。

1 计算方法

如图1所示由人工边界和地表包围的区域结构-地基系统，运动方程为：

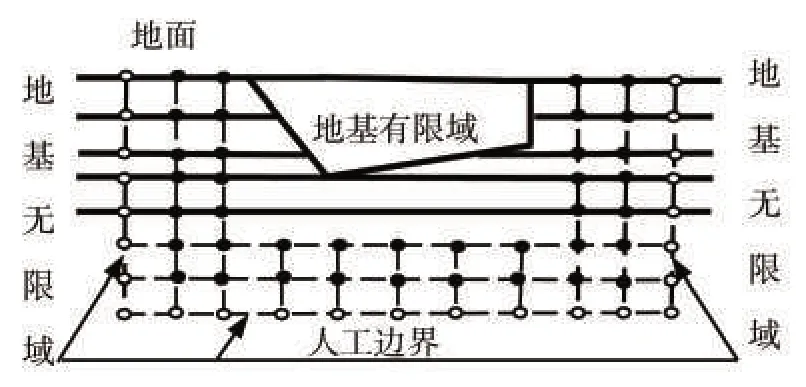
图1 结构-地基系统动力反应分析示意图Fig.1 Schematic diagram of dynamic response analysis of structure-foundation system

式中：M为质量矩阵；C为阻尼矩阵；K为刚度矩阵；P为外力矢量。

在地震波作用下，本文所讨论的波动问题有2 个问题需要解决好：一是边界问题；二是地震波的输入问题，且这2个问题是相关联的。

（1）人工边界

本文的人工边界采用的是多次透射公式（Multi-Transmitting Formula，简记为“MTF”）［21］。设某一入射波以人工波速ca沿x轴从左侧射向人工边界点0（图2），记点j在p时刻的位移表达式为=u(pΔt,jΔx)，j和p为整数，Δt为时间步距，Δx为空间步距，若Δt=Δx/ca，则可直接用与人工边界垂直方向上的内部节点的位移确定：

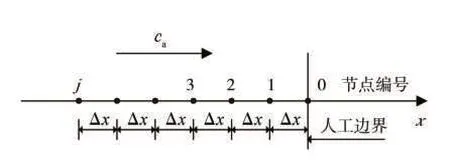
图2 人工边界附近节点编号，一维波动模型图Fig.2 Node number near artificial boundary，one-dimensional wave model

式中：

由于MTF模拟的是外行波，即散射波us，其表达式为：

式中：us散射波位移；u为全波场位移；ur为参考波场的位移（对底边界，参考波场可直接取输入场，对侧边界，则通常取为自由场。令多次透射公式（2）中u=us，将式（4）代入式（2）中，则：

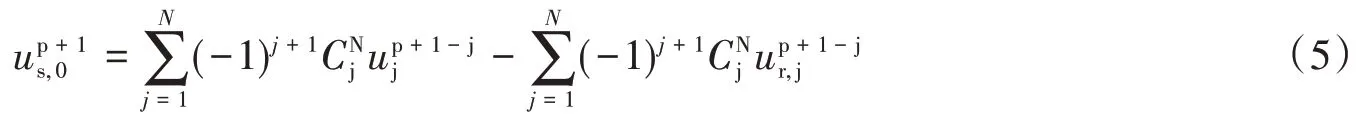
（2）地震波的输入

假定输入地震波为位移，则输入面为人工边界节点所在位置，人工边界点的全波场位移为：

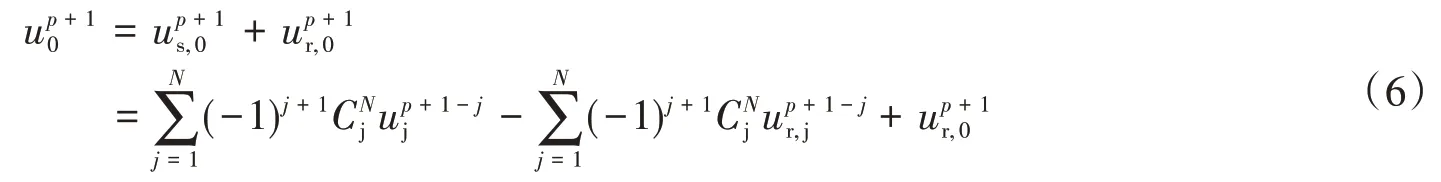
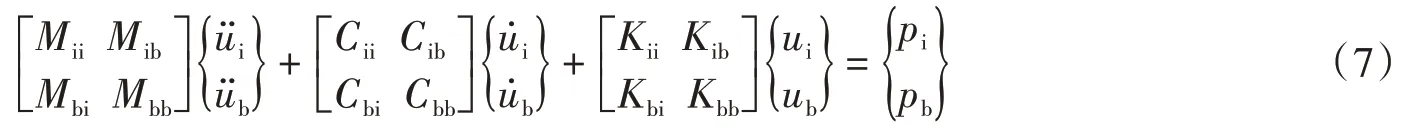
式中：下标i表示内节点（包括自由表面节点）；b表示边界节点。对于散射问题，方程（7）的右边荷载项为0，方程（7）就变成已知边界点ub的位移求解内节点位移问题。对于波源问题，方程（7）的右边pb为0，方程（7）就变成已知边界点ub的位移和pi求解内节点位移问题。只要选择一种合适的数值积分格式，两种情形都很容易对方程（7）进行求解。

（3）有限元数值模拟的网格尺寸要求

解析方法给出的场地地震响应一般是基于无量纲频率的谱比（或称谱放大系数），其中无量纲频率定义为：

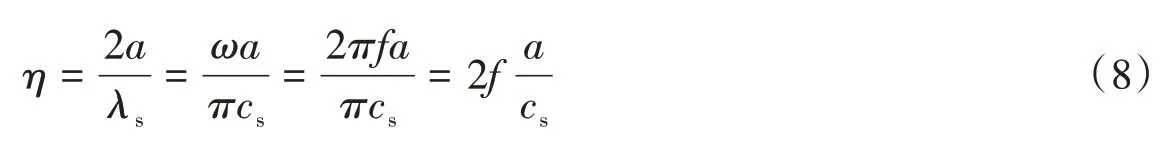
式中：a为沉积谷地地形半宽；λs为土层介质中剪切波波长；cs为土层剪切波速；ω为圆频率。参数η表示沉积谷地宽度与土层介质中剪切波波长之比，η值越大，其入射波波长越小，对应的频率f越高。

进行有限元数值模拟时，网格尺寸一般需要满足在一个有意义的波长内包含有10 个单元网格，如下列关系式：

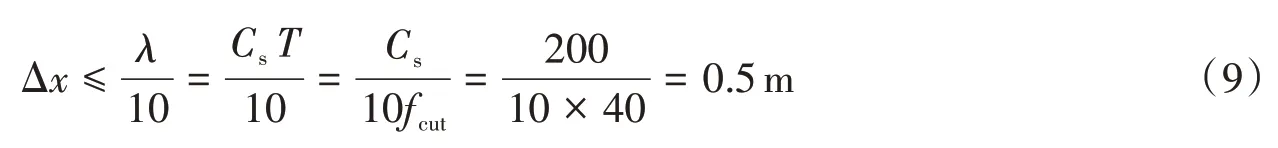
式中：λ表示为入射波的波长；Cs表示为沉积介质中的剪切波速；T表示为入射波的周期；fcut表示为入射波的截止频率，本文取40 Hz。根据式（9），确定网格尺寸Δx=0.5 m；根据稳定性条件，时间步距dt=0.000 25 s。

2 方法验证

算例1：均匀半空间沉积谷地

采用文献［13，26］相同的沉积谷地模型和介质参数作为算例（图3），以垂直入射脉冲波的计算结果验证本文的有限元方法。计算参数为无量纲频率η=2a/λs，泊松比μ=1/3，沉积谷地与半空间的剪切波速之比为200/400，压缩波速之比为400/800，介质密度之比1.4/1.8，半圆形沉积谷地半径取a=25 m。

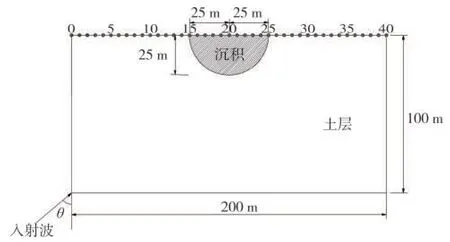
图3 方法验证模型图-均匀半空间沉积谷地Fig.3 Model diagram of method validation-alluvial valley embedded in a uniform half-space

在上述模型的地表取41个观测点，编号分别为0～40，图4 为41 个点水平方向和竖直方向的时程图。首先将场地各点的位移进行傅里叶变换，得到频域响应的傅里叶谱，再计算与入射脉冲波的傅里叶谱的比值。文献［13］和文献［26］给出了入射角θ=0°，无量纲频率η=1的解析解。图5为本文计算结果与文献［13］和文献［26］进行比对，从图中的对比结果可以发现：采用本文方法得到的数值模拟结果与解析解吻合，由此验证了本文方法的正确性。

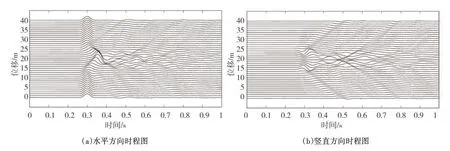
图4 均匀半空间沉积谷地地表时程图Fig.4 Time history diagram of surface-alluvial valley embedded in a uniform half-space

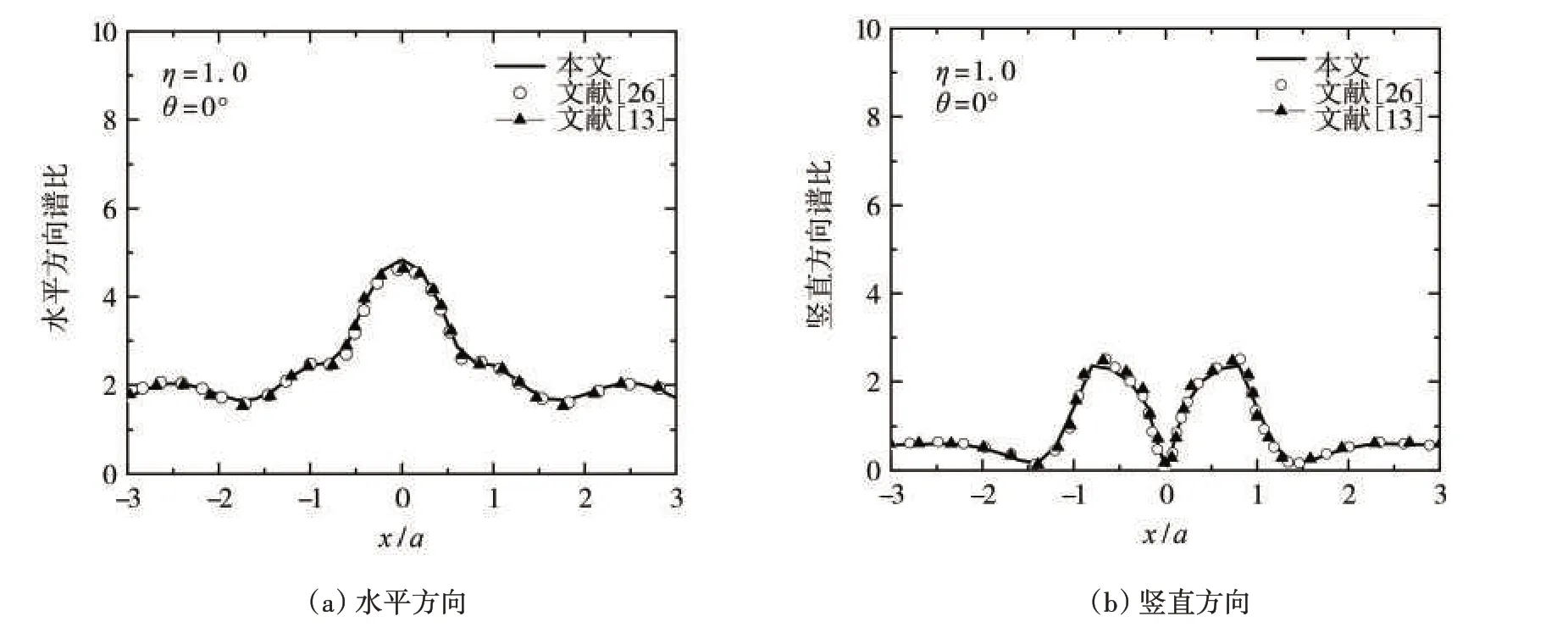
图5 本文计算结果与文献［13］和文献［26］结果的比较Fig.5 Comparison of results from this paper and Reference［13］，［26］

算例2：层状半空间沉积谷地

采用文献［27］的层状半空间中半圆沉积地形模型和介质参数（图6），同样以垂直入射脉冲波的计算结果为例验证本文方法。沉积谷地与土层的剪切波速之比为200/400，土层与基岩的剪切波速之比为400/800；沉积谷地与土层的压缩波速之比为400/800，土层与基岩的压缩波速之比为800/1 600。沉积谷地与土层的介质密度之比1.6/2.4，土层与基岩的介质密度之比2.4/3.2，泊松比均为μ=1/3，半圆形沉积谷地半径取a=25 m。

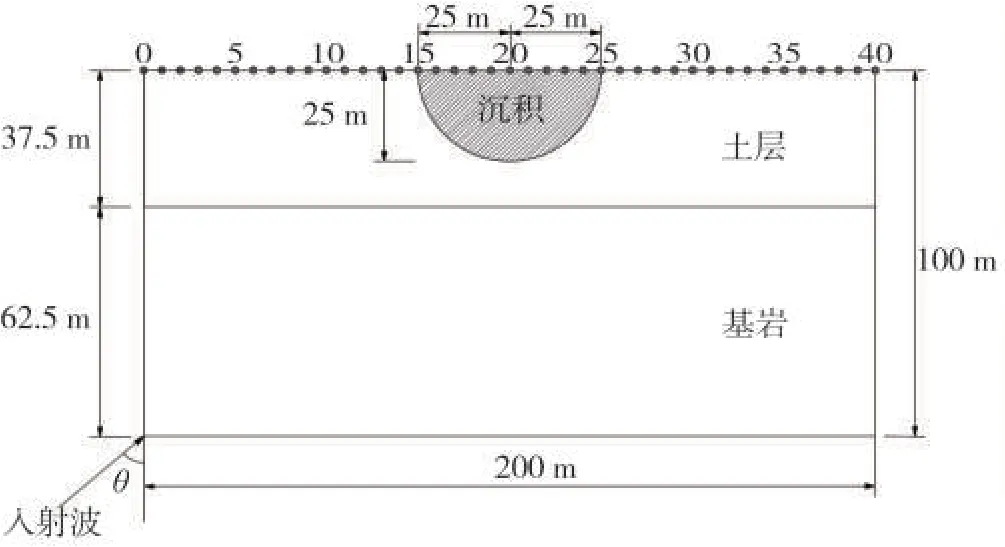
图6 方法验证模型图-层状半空间沉积谷地Fig.6 Model diagram of method validation-alluvial valley embedded in a layered half-space

在上述模型的地表取41个观测点，编号分别为0～40，图7为41个点水平方向和竖直方向的时程图。与算例1 的方法相似，首先将场地地表各点的位移进行傅里叶变换，得到频域响应的傅里叶谱，再计算与入射脉冲波的傅里叶谱的比值。文献［27］给出了入射角θ=0°，无量纲频率η=0.5 的解析解。图8 为本文计算结果与文献［27］的比对，从对比结果可以发现：采用本文方法得到的模拟结果与FRANCISCO 等［27］给出的解析解吻合，由此验证了本文方法的正确性。

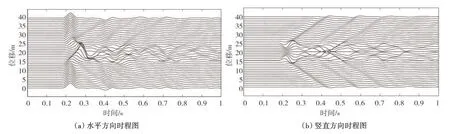
图7 层状半空间沉积谷地地表时程图Fig.7 Time history diagram of surface-alluvial valley embedded in a layered half-space

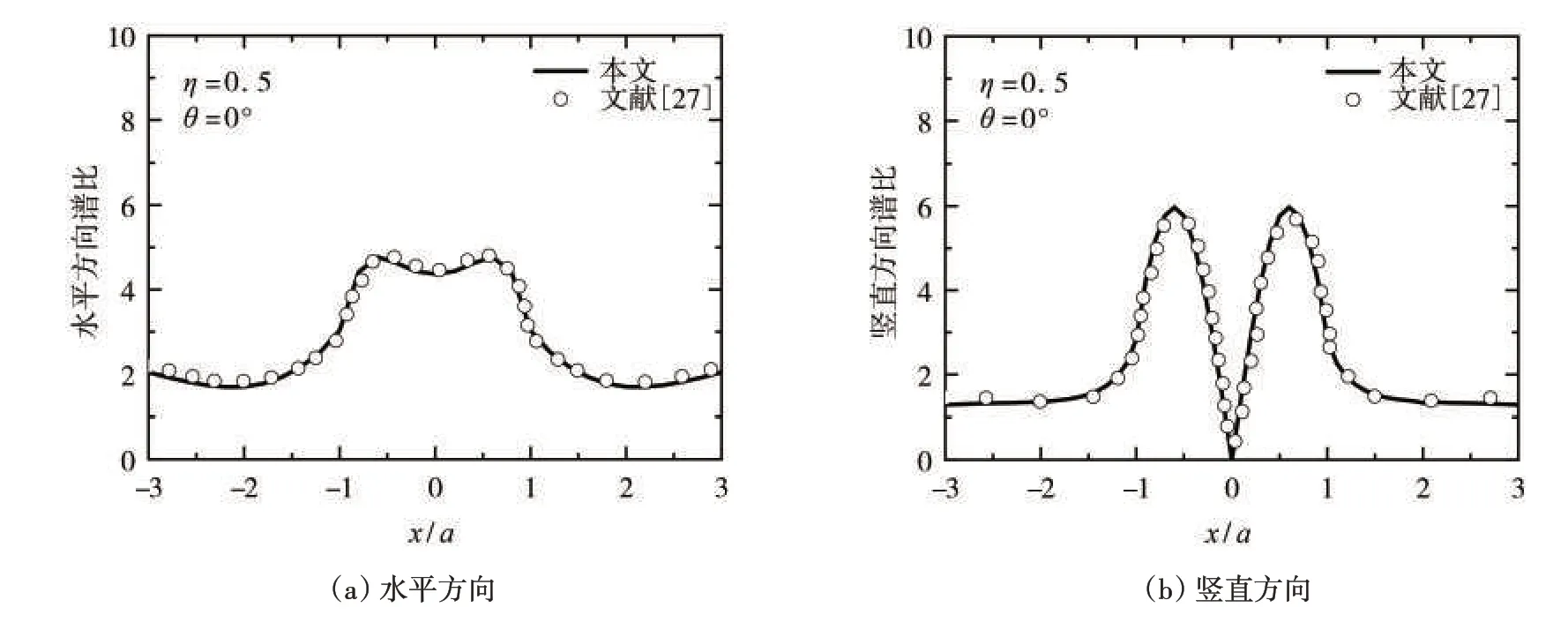
图8 本文计算结果与文献［27］结果的比较Fig.8 Comparison of results from this paper and Reference［27］

3 输入波形和计算模型

假定入射SV 波为脉冲波（图9），输入波的截止频率大约为fcut=40Hz。有限元计算模型为半空间上有一简单圆弧形沉积，长300 m，高100 m，如图10所示。沉积介质的密度为1 600kgm3，土层介质的密度为1 800kgm3，层状半空间中基岩介质的密度为2 200kgm3，泊松比均为1/3。

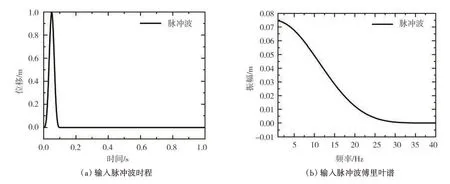
图9 输入脉冲波时程及相应傅里叶谱Fig.9 Time history and Fourier spectrum of Pulse wave

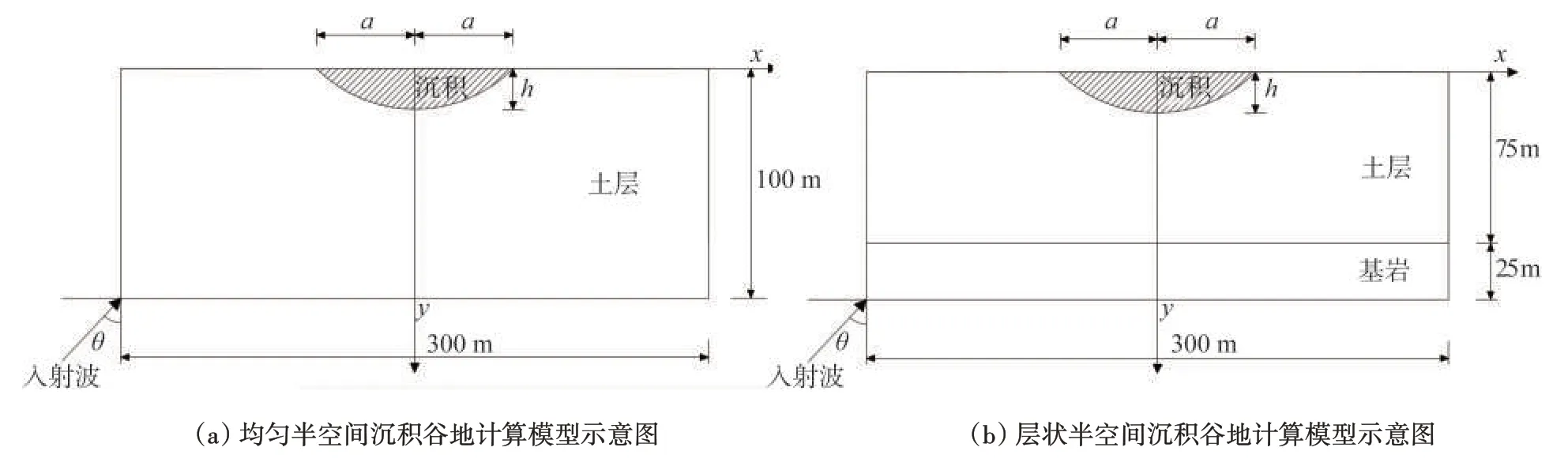
图10 沉积谷地计算模型示意图Fig.10 Calculation model of alluvial valley

本文假定了4个计算模型，模型参数见表1。模型1和模型2为均匀半空间沉积谷地模型；模型3和模型4为层状半空间沉积谷地模型，其中土层厚度为75 m，基岩厚度为25 m。

表1 模型参数Table 1 Model parameters

根据计算模型中沉积谷地半宽与土介质特性，由式（8）可得无量纲频率与实际频率对应关系见表2。

表2 无量纲频率对应的实际频率（Hz）Table 2 Actual frequency（Hz）corresponding to the dimensionless frequency

4 算例与分析

采用本文提出的有限元模拟方法研究沉积河谷地形对平面SV 波的宽频散射，给出了不同入射角度和河谷深宽比等参数下的单频结果。SV波入射角度分别为θ=0°、15°、25°，无量纲频率分别为η=0.25、0.5、1、2、4、6。

4.1 均匀半空间沉积谷地

图11 给出了不同角度SV 波入射下均匀半空间半圆形沉积河谷（模型1，h/a=1.0）地表位移谱放大系数β。垂直入射（θ=0°）情形下：沉积河谷上方水平方向的放大系数β基本大于2.0，在x/a=0 及其附近处最大；除了频率η=0.25，放大系数β=2.71，其它频率的放大系数β在4.0～6.0 之间；在＞1 范围内，放大系数β大于2 的情况不多。随着入射角度增大，如分别为θ=15°、25°，放大系数β略有增大；且随着频率的增大，放大系数β的最大值向入射波的异侧偏移，但偏移的幅度不大。

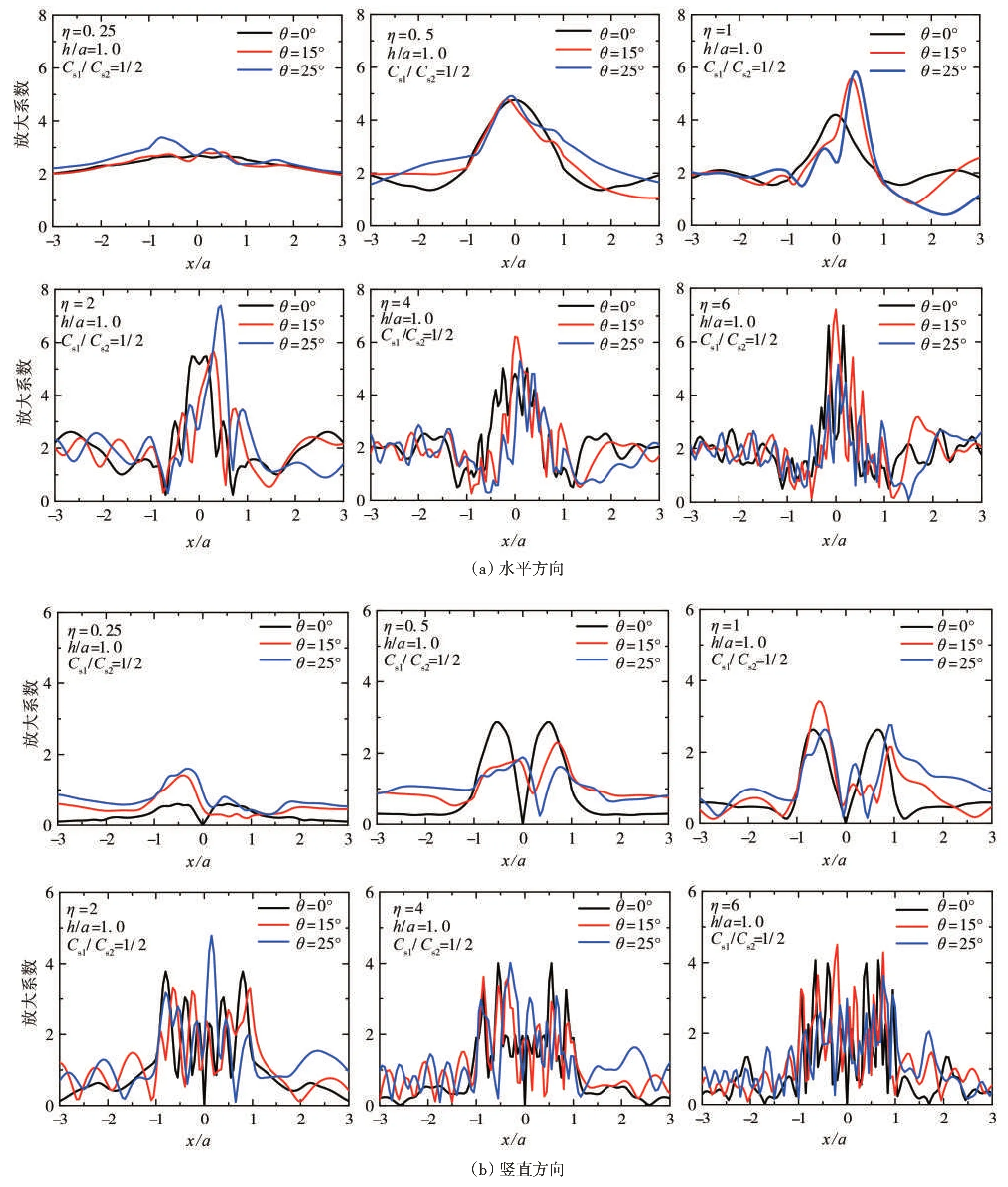
图11 SV波入射下均匀半空间半圆形沉积河谷地表位移谱放大曲线（模型1）Fig.11 Amplification curve of surface displacement spectrum of semicircular alluvial valley in uniform half space under SV wave incidence（model 1）

竖直方向放大系数的特点与水平方向相似，但β要小于对应的水平方向，特别是当频率较小时，如η=0.25，各种情形下整个地表范围的放大系数β均小于2；另外，在x/a=0及其附近处放大系数β最小。

图12 给出了不同角度SV 波入射下均匀半空间浅圆弧形沉积河谷（模型2，h/a=0.4）地表位移谱放大系数β。垂直入射（θ=0°）情形下：沉积河谷上方水平方向在η=0.25 时的放大系数β接近于2，没有反映出地形的影响，随着频率的增大，沉积河谷的影响逐渐明显，放大系数β也有增大，但也少有大于6.0；在＞1 范围内，所有频率的放大系数β大于2 的情况也不多。随着入射角度增大，如分别为θ=15°、25°，频率较小时的放大系数β略有增大，频率增大时不明显；且随着频率的增大，放大系数β的最大值向入射波的异侧偏移，但偏移的幅度不大。竖直方向的放大系数的特点与水平方向相似，但放大值要小于水平方向。在＜1 范围内，相对于半圆形沉积河谷，浅圆弧形沉积河谷在频率较小阶段的放大系数较小。

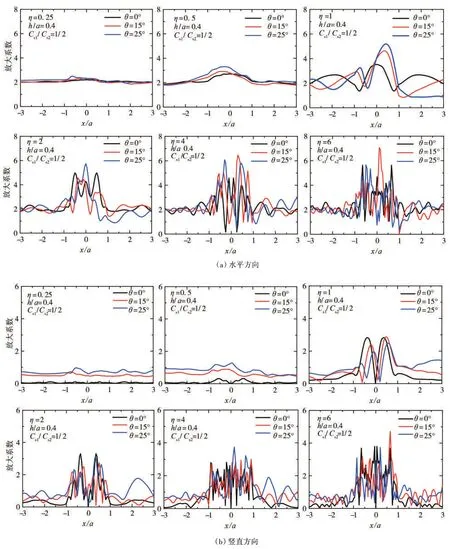
图12 SV波入射下均匀半空间浅圆形沉积河谷地表位移谱放大曲线（模型2）Fig.12 Amplification curve of surface displacement spectrum of shallow arc alluvial valley in uniform half space under SV wave incidence（model 2）

4.2 层状半空间沉积谷地

图13给出了不同角度SV波入射下层状半空间中半圆形沉积河谷（模型3，h/a=1.0）地表位移谱放大系数β。η=2.0时的放大系数β相对最大。随着入射角度增大，放大系数β的变化明显，较均匀半空间中半圆形沉积河谷的大；且随着频率的增大，放大系数β的最大值向入射波的异侧偏移，但偏移的幅度不大。竖直方向放大系数的特点与水平方向相似，但β值要小于对应的水平方向。

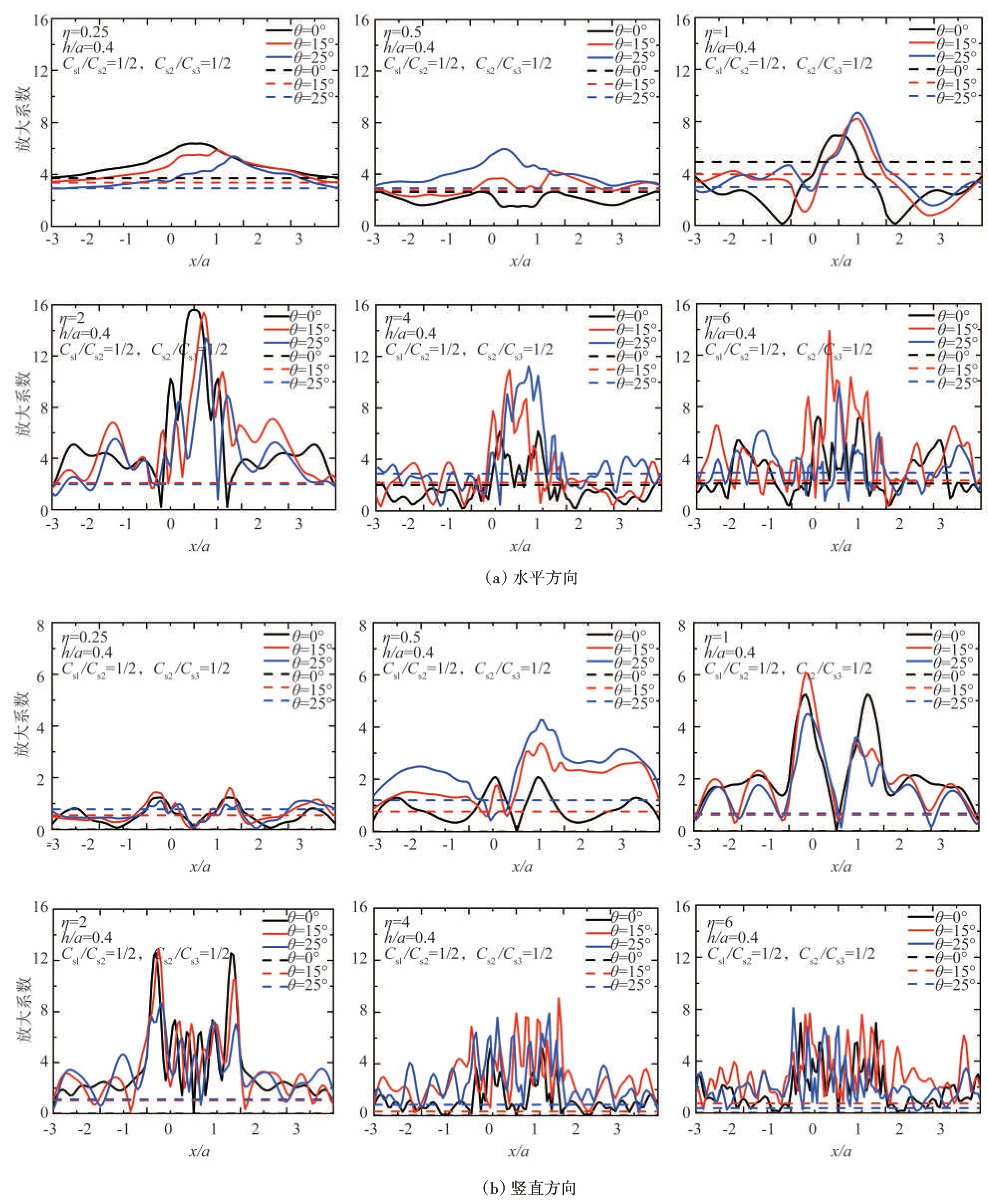
图13 SV波入射下半空间半圆形沉积河谷地表位移谱放大曲线（模型3），其中虚线为对应的半空间地表位移谱放大曲线Fig.13 Amplification curve of surface displacement spectrum of semicircular alluvial valley in layered half space under SV wave incidence（model 3），and the dotted line is displacement spectrum amplification curve corresponding half-space ground

图14给出了不同角度SV波入射下层状半空间中浅圆弧形沉积河谷（模型4，h/a=0.4）地表位移谱放大系数β。在＜1范围内，相对于层状半空间中半圆形沉积河谷，层状半空间中浅圆弧形沉积河谷在较小频率阶段的放大系数较小，频率较大时的放大系数相差不大。

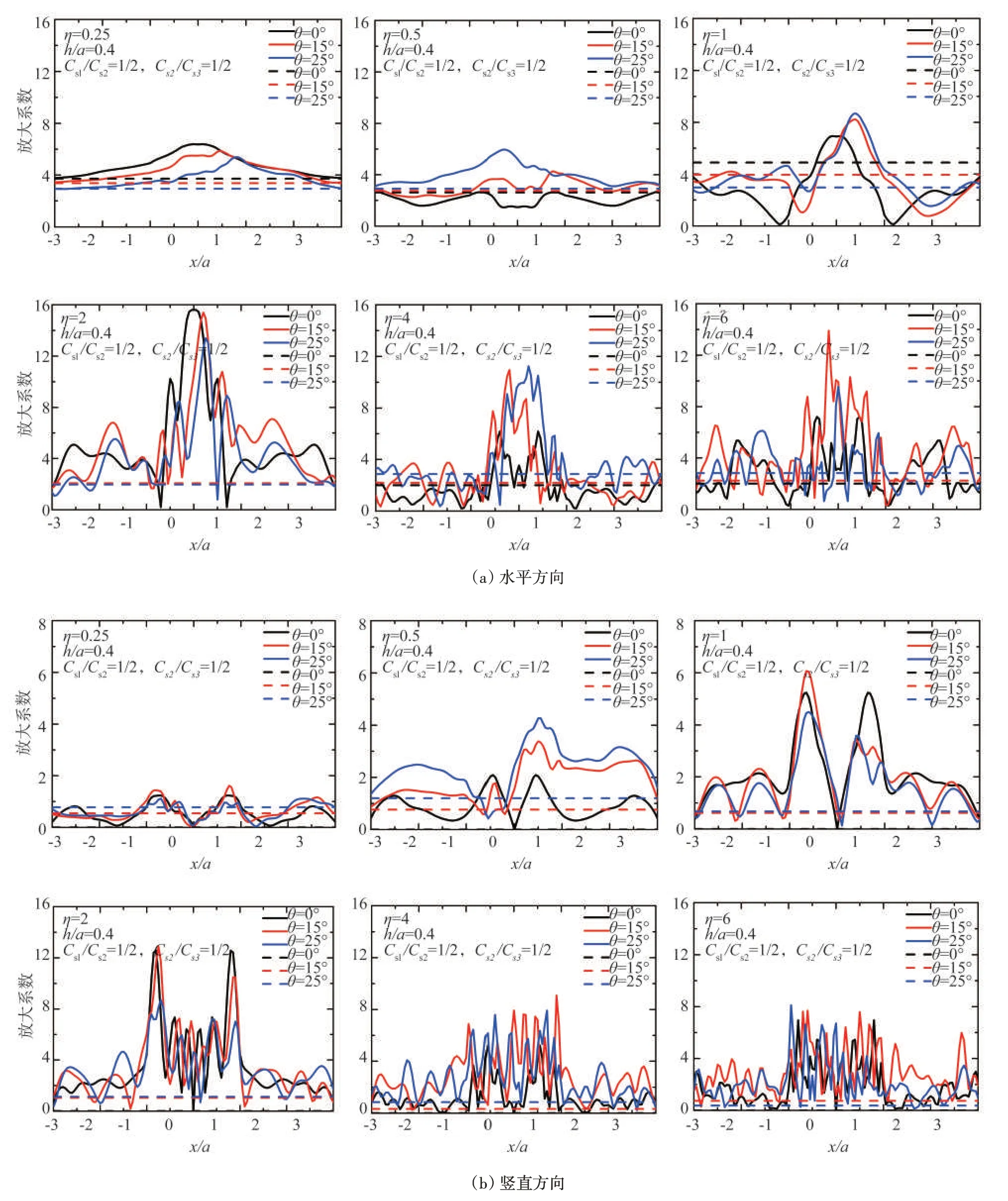
图14 SV波入射下层状半空间浅圆形沉积河谷地表位移谱放大曲线（模型4），其中虚线为对应的层状半空间地表位移谱放大曲线Fig.14 Amplification curve of surface displacement spectrum of shallow arc alluvial valley in layered half space under SV wave incidence（model 4），and the dotted line is displacement spectrum amplification curve correspondinglayered half-space ground

图13-14 中同时给出了与模型3 和模型4 对应的半空间和层状半空间地表位移谱放大曲线（见图中虚线）。对于半空间和层状半空间模型，其地表位移谱放大结果对应相同的频率在图中表示为直线。与半空间和层状半空间圆弧形沉积河谷地表位移谱放大曲线相比，半空间和层状半空间的场地放大效应明显偏小；但有极少数情形，半空间和层状半空间的场地放大效应反而较大，这与盆地内的介质特性有关。

5 结论

本文采用有限元数值模拟方法研究了均匀半空间和层状半空间中圆弧形沉积谷地对入射平面SV 波的散射问题，并分析了河谷深度、入射角度和频率等因素的影响，得出一些有意义的结论：

（2）层状半空间沉积河谷的β比均匀半空间沉积河谷的大，其中层状土介质的因素很大。总体上，层状半空间半圆形和浅圆弧形沉积河谷的放大系数β的变化趋势，与均匀半空间半圆形和浅圆弧形沉积河谷相似。

（3）入射角度对放大系数β有影响，特别是频率η较小阶段，随着频率的增大，β有增大；另外且随着频率的增大，放大系数β的峰值向入射波的异侧偏移，但偏移的幅度不大。

（4）竖直方向的放大系数β与上述水平方向的类似，＞1范围内的地表放大系数β较大。但与水平方向的地表放大系数β的峰值总是出现在=0 附近不同，竖直方向的放大系数β的谷值一般出现在=0附近。

（5）大多情形下，半空间和层状半空间的场地放大系数β比层状半空间圆弧形沉积河谷的放大系数β明显偏小。