俯冲带板内地震竖向位移谱阻尼修正系数模型研究

王本三，靳羽阳，刘名吉

（山东建筑大学土木工程学院，山东济南 250000）

引言

国内外大多数抗震设计规范都给出水平向5%阻尼比绝对加速度或伪加速度规范设计反应谱［1－7］，而我国《核电厂抗震设计规范》（GB50267-97）［4］、欧洲抗规（EC8）［5］、美国抗规（FEMA P-750）［7］等也同时标定了竖向5%阻尼比设计反应谱。大多数的地震动衰减关系（GMPEs）也一般基于5%阻尼比水平，如ZHAO等［8］、POWER 等［9］、BOZORGNIA 等［10］和CAMPBELL 等［11］。然而随着高层建筑与消能减震装置的应用，不同阻尼比的结构日趋增多。现有规范通常采用阻尼修正系数（Damping Modification Factor，DMF）（定义为式（1）［1－7］，以位移谱为例）对其调整得到非5%阻尼比下的设计反应谱。

式（1）中：Bd为位移谱DMF；T为谱周期；ζ为阻尼比；Sd（T，ζ）和Sd（T，0.05）分别表示周期为T，阻尼比为ζ与阻尼比为0.05时的位移反应谱。

DMF 模型研究最初是由NEWMARK 等［12］展开，基于28 条冲积层地震记录和加州San Fernando 地震数据（1971）给出了仅与阻尼比有关的DMF表达式，后被用于美国抗规［7］。随着研究的深入，人们发现谱周期、场地条件和震源因素等对DMF的影响不容忽视。马东辉等［13］强调了DMF与周期密切相关并建议采用分段形式的DMF 模型；LIN 等［14］基于1 037 条地震记录，统计研究了考虑场地类别影响的DMF，并讨论了振动周期、阻尼比和场地类别对DMF的影响；CAMERON 等［15］考虑震源因素，研究发现震源类型及场地条件等对地震动频率有显著影响，进而影响DMF 模型；郝安民等［16］考虑矩震级影响，给出各类场地下DMF 表达式；ATKINSON 等［17］建立了适用于北美东部的DMF 模型，并探究了震级和震源距对DMF 的影响；REZAEIAN 等［18］基于NGA-West2数据建立了考虑震级与震源距的DMF模型。然而上述研究，很少有涉及地震类型因素影响的DMF模型，更少有竖向反应谱的DMF模型提出。

如今，愈多实测数据显示：高烈度区及近断层区域的竖向地震作用甚至超过水平地震，且随着各种大跨及超高体系、隔震结构的广泛应用，竖向地震作用的影响尤为突出［19］。现有规范对其计算过于粗糙，如我国《建筑抗震设计规范》（GB50011-2010）［1］规定取竖向地震动的影响系数最大值为水平地震动的65%，而《公路桥梁抗震设计细则》（JTG/TB02-01-2008）［20］中则用分段的V/H 反应谱比表示竖向地震动作用。事实上由于竖向地震动与水平向地震动的显著差异导致简单的V/H 模型无法准确描述竖向地震动的反应谱特征［21－22］。BOZORGNIA 等［21］对美国Northridge 地震（1994）的研究表明：V/H 反应谱比受震级、周期及震源距的影响且在近场区和短周期内远高于通常假定的2/3。周正华等［22］在对台湾集集地震（1999）竖向反应谱的研究中发现：V/H反应谱比是周期的函数且场地条件对谱比值影响显著。可见：使用固定的V/H比值或简单的V/H模型并不尽合理；此外也有学者直接对竖向地震动衰减关系进行研究，如ZHAO等［23］和JIANG等［24］分别建立了用于俯冲带浅壳和上地幔以及板内地震的竖向地震动衰减关系。另一方面，传统的设计方法是基于结构总加速度乘以质量（即惯性力）来求解结构在惯性力作用下产生的位移，因为结构是否达到破坏状态是由结构部件相对位移决定，如结构层间相对位移；对于结构水平向地震反应，PRIESTLEY［25］于2000年提出了更为直观的基于结构位移的抗震设计方法。在这种设计理论中可以直接使用结构位移反应谱［25－27］。然而由于不同阻尼比的反应谱模型相对较少，一般根据伪谱关系式（2）由加速度反应谱SA来计算位移反应谱SD：

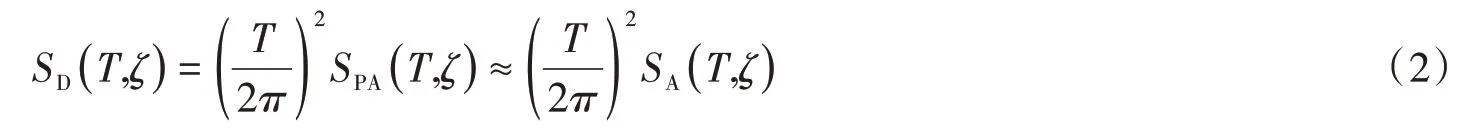
式（2）中：T为谱周期；ζ为阻尼比；SD、SA和SPA分别为相对位移谱、绝对加速度谱和伪加速度谱。值得注意的是，当且仅当ζ较小时（ζ≤0.05），大多数谱周期SPA≈SA，但在高阻尼比或长周期时简单使用此关系进行转换，必将高估结构弹性恢复力，体现不出消能器耗能的优势。故直接基于位移谱研究其DMF模型是合理且必要的。

ZHAO等［28］研究证实：反应谱与地震类型显著相关。故本文考虑地震类型因素，以日本俯冲带地区4 695条板内地震记录竖向分量为基础数据，运用固定效应法分别给出四类场地下的竖向位移谱DMF 模型，并根据随机效应模型分析各参数对DMF 模型误差产生的影响［37］，以期更好地完善模型。本文建立的DMF 模型可为我国俯冲带地区（如台湾和南海）的抗震设计提供参考。

1 强震数据来源与处理

该研究所需地震动数据来源于日本K-NET 和KiK-net 强震动台网（https：//www.kyoshin.bosai.go.jp/）。目前台站总数达1 700多个，采用高灵敏度强震仪，可以记录3个方向（东西、南北和竖向）地震动分量以及基岩深度20 m 范围内的钻孔资料，最大采样频率高达200 Hz，为获取丰富可靠的数据资料提供了强大的技术支撑。

筛选出136 次板内地震事件的4 695 条地震记录（Mw≥5.0）作为该研究的基础数据。方法如下：依据美国地质调查局（USGS，http：//earthquake.usgs.gov/data/slab/）提供的slab1.0 模型和ZHAO 等［28］采用的日本地震分类手段，分离出俯冲带板内地震（Subduction Slab）。板内地震多发生在俯冲的海洋板块内，插入角度大，震源深度通常在50 km 以上。随后参考ZHAO 等［29］基于场地周期Ts见式（3）的场地分类方法，将地震记录分成SCI～SCIV四类场地进行研究（期间通过基线校正与滤波处理）［30］。场地分类标准与记录数量见表1。

表1 四类场地分类标准与记录数量Table 1 Site classification criteria and record quantity of four kinds of sites

Ts计算式如下：

式（3）中：Ts为场地周期，单位为s；H为地表面至基岩顶部的深度，单位为m；Vsite为基岩上覆土层的加权平均剪切波波速，单位为m/s。

2 建立DMF均值模型

2.1 数据分析

基于4 695 条俯冲带板内地震记录（Mw≥5.0），首先计算出36 个谱周期（0.01～5.0 s）和14 个阻尼比（1%～30%）的相对位移反应谱，进而求得对应的DMF 几何均值`Bd作为回归分析与残差分析的基础数据。谱周期编号见表2，阻尼比编号见表3。

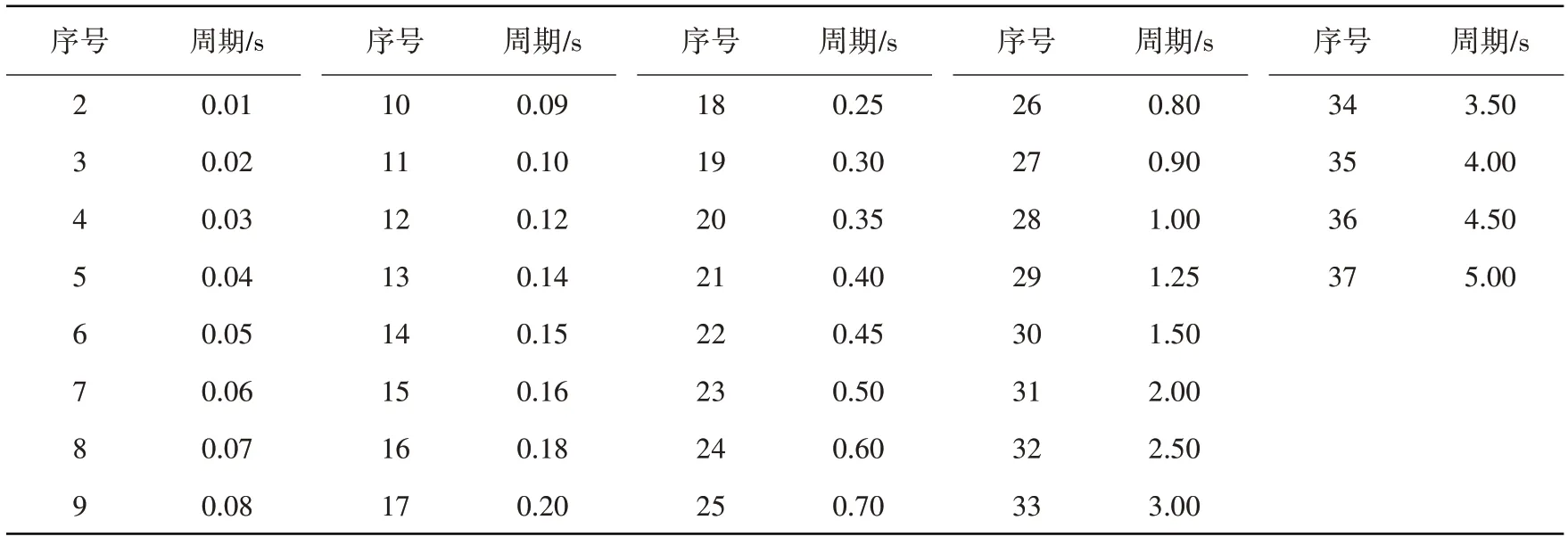
表2 谱周期编号Table 2 Number of spectral periods

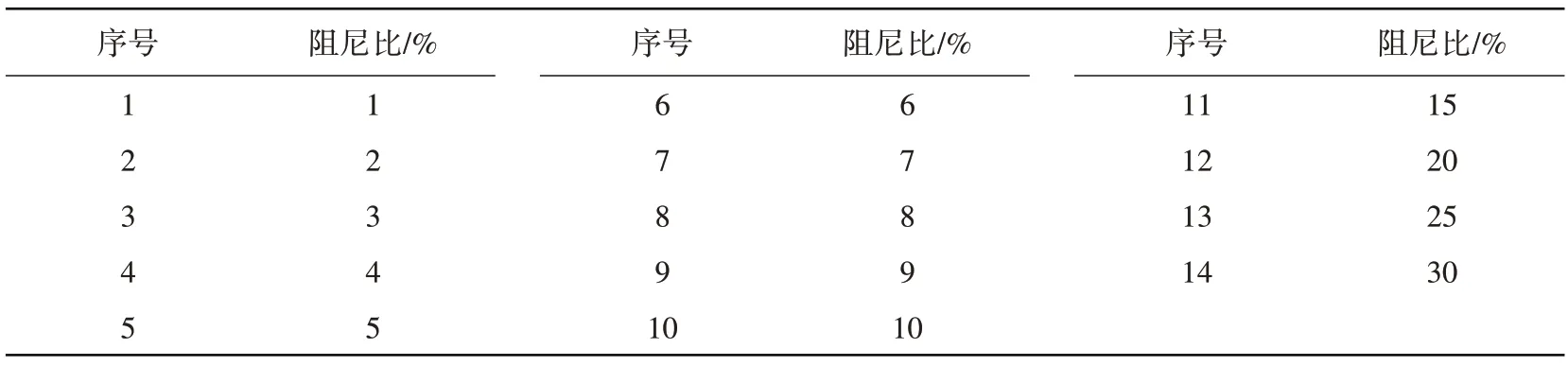
表3 阻尼比编号Table 3 Number of damping ratios

图1（a）至图1（d）给出了四种阻尼比（1%、3%、15%和30%）下各类场地的DMF 均值与谱周期T 的分布图。图中可见：（1）整体来看：指定阻尼比时，四类场地的DMF均值随谱周期的变化趋势相同。同一谱周期，阻尼比越大，四类场地的DMF 均值越小，与理论相符。（2）极短周期（T≤0.02 s）时，DMF 均值都等于1，与场地条件无关，同时符合单自由度结构地震反应放大系数在自频非常大时动力反应与阻尼比无关。（3）谱周期处于0.03～0.12 s 范围时，SCI 与其他三类场地区别较大；0.32 s 之后，SCIV 与其他三类场地有较大的差异。（4）随着谱周期的增大，DMF均值趋向于1，符合长周期时位移反应谱趋于地表最大位移。（5）阻尼比小于5%时，四类场地的DMF均值先增后减；阻尼比大于5%时则相反。

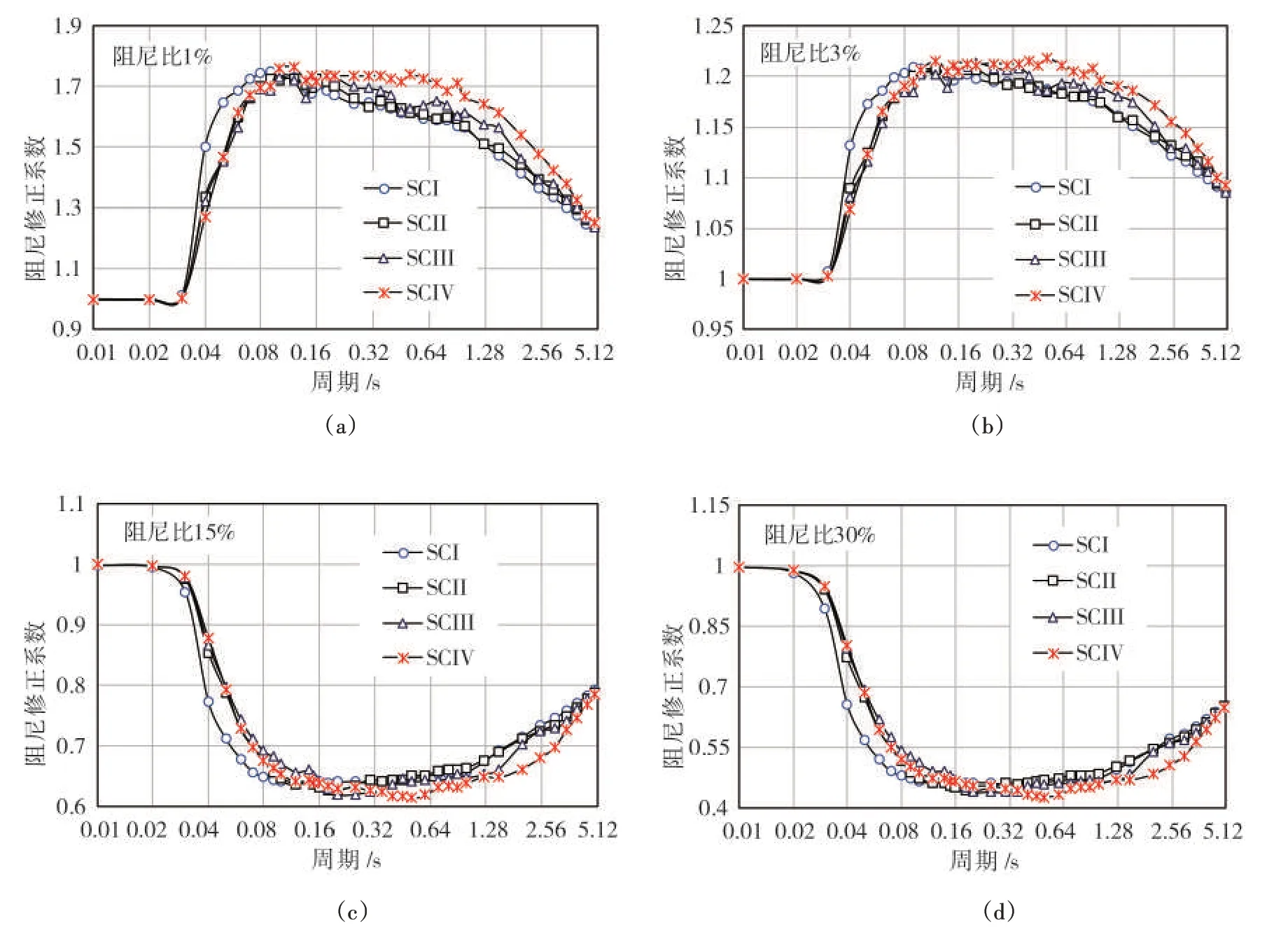
图1 SCI～SCIVDMF均值分布曲线（阻尼比为1%、3%、15%、30%）Fig.1 Curve of mean values of DMF for four site classes（ζ=1%、3%、15%、30%）

2.2 显著性检验

为探究分场地建立DMF模型的必要性，运用Z检验方法（取α=0.05，|Z|≥1.96）对数据进行统计检验，即当Z值落在拒绝域内时，表示两组数据差异显著。统计量Z表示为：

为直观显示，基于四种代表性阻尼比（1%、3%、15%和30%）给出其两两场地间Z值趋势变化图如图2所示。分析得出：（1）由图2（a）至图2（c）可见：当谱周期小于0.1 s 时，对应 |Z|统计值大于1.96，说明SCI 与SCII、SCI与SCIII和SCI与SCIV均值数据显著不同。可能受到场地共振影响，导致短周期内SCI的位移谱与其他场地相比较大，而其它场地的位移谱差别相对较小。（2）由图2（c）和图2（e）可见：谱周期0.32～5 s 范围时，四种阻尼比对应的 |Z|统计值均大于1.96；图2（c）中谱周期0.02～0.08 s 时也符合这一情况，说明均值数据统计上显著不同。（3）图2（d）中，近半数谱周期对应的 |Z|统计值大于1.96。由（4）图2（f）可见：当阻尼比为30%，周期小于0.08 s时 |Z|统计值远大于1.96，数据统计上显著不同。说明SCIII与SCIV 在短周期高阻尼比下的均值数据差别较大。综上，通过对 |Z|统计量的检验发现，分场地建立不同的DMF模型是非常必要的。

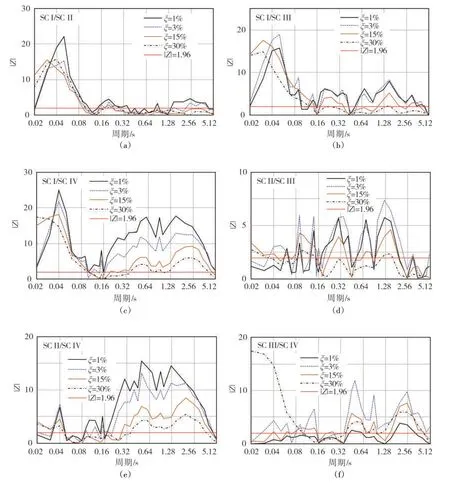
图2 SCI～SCIV间Z检验统计值Fig.2 |Z|values for statistical tests between each pair of SCI～SCIV sites

2.3 建立DMF均值模型

在建立DMF 均值模型时，参考STAFFORD 等［31］和HATZIGEORGIOU［32］关于均值模型的经验公式，同时考虑阻尼比与周期的影响［33-36］，给出DMF均值关于阻尼比对数二次项的回归方程式，见式（5）：

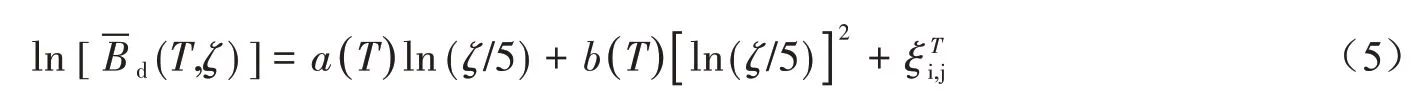
运用固定效应方法对系数a和b进行回归，得到不同谱周期下的a和b值。表4给出了回归后的系数值a和b（谱周期0.01 s与0.02 s系数值为0，表中不再给出（下同）；谱周期0.03 s、0.04 s和0.05 s不进行函数化，系数值可由插值给出；谱周期0.06 s 之后进行谱周期平滑，必要时进行迭代）。不同阻尼比不同周期下的系数可由表中数据插值得到。

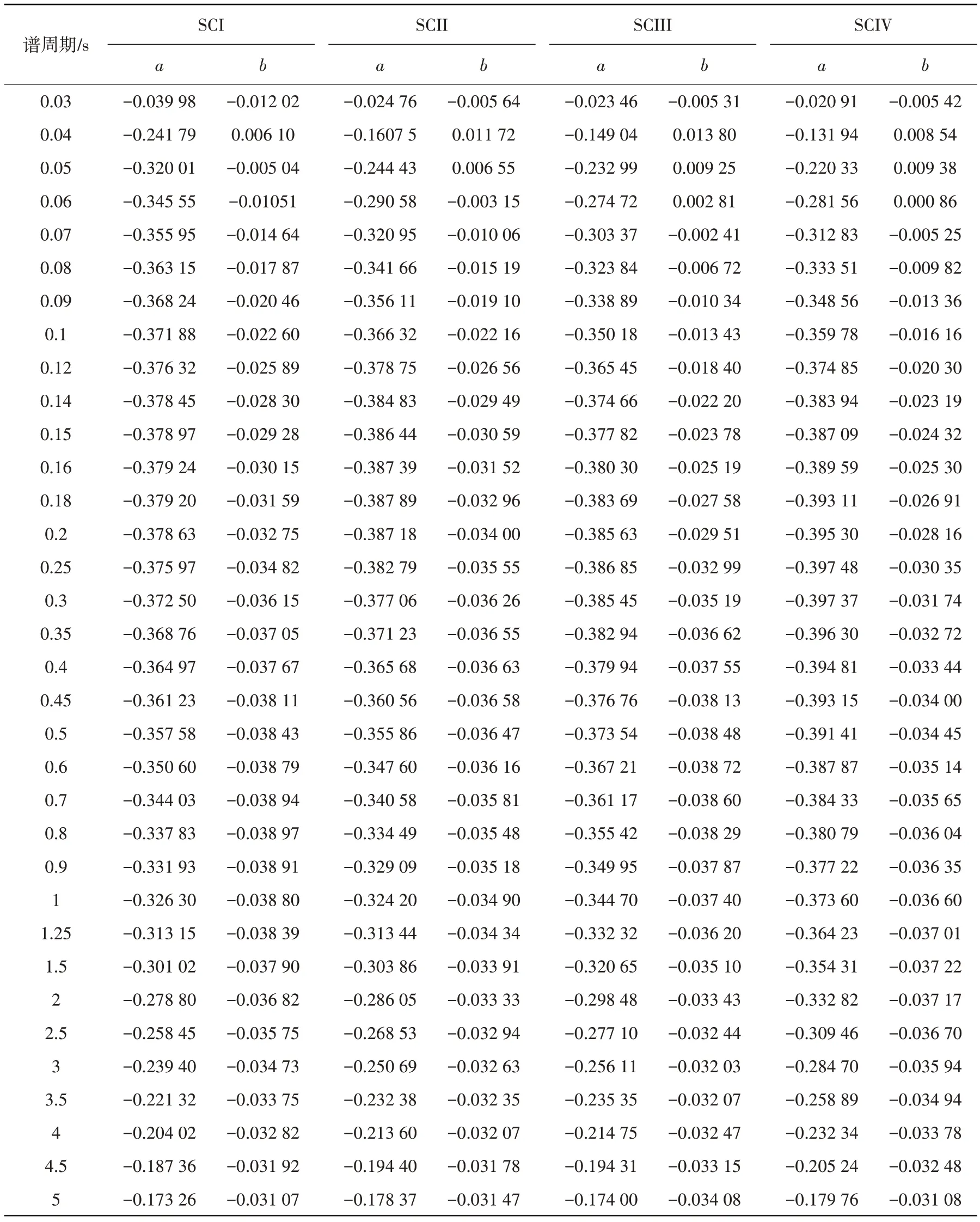
表4 DMF模型回归系数Table 4 Model coefficients for theDMF models

图3 给出了四类场地下回归系数a、b 与谱周期的变化图。其中散点表示模型系数由插值得到，实线表示系数值经谱周期函数化。由图3（a）可见：谱周期小于0.1 s 及谱周期0.64～3 s 内，SCI 与SCIV 模型一次项系数分别与其他三类场地有较大差异。图3（b）显示：各类场地模型的二次项系数差异较小。

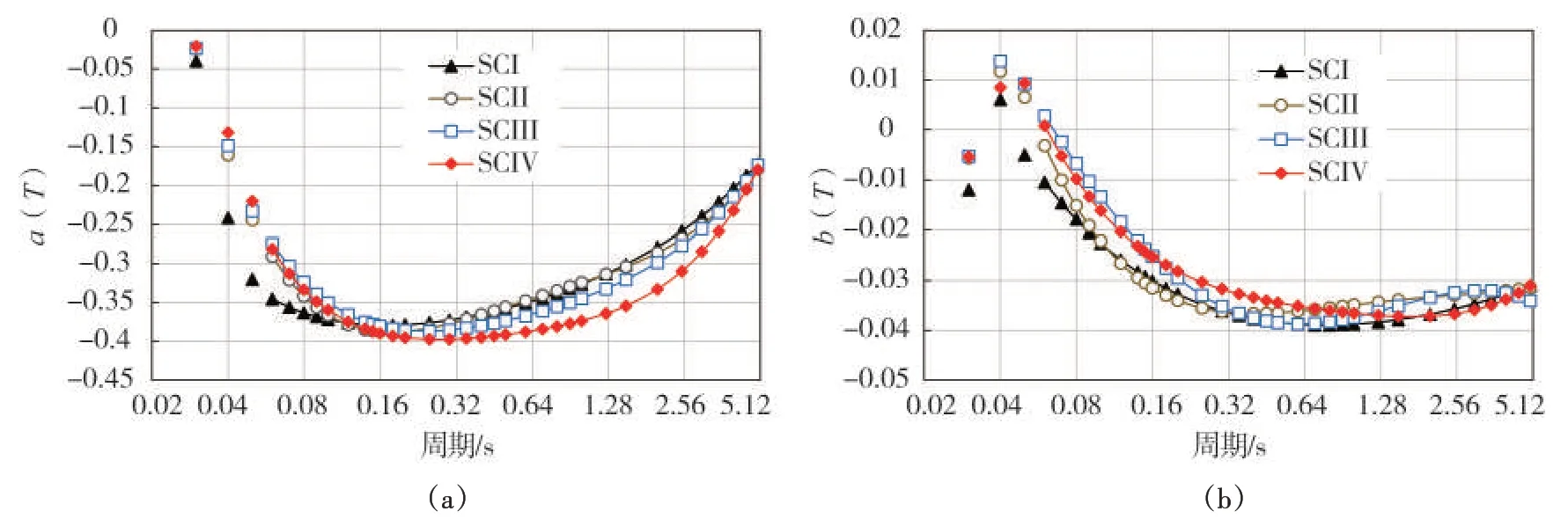
图3 系数a和b随谱周期分布图Fig.3 Distributions of coefficients with spectral periodsfor SCI～SCIV sites

图4 给出了DMF 均值拟合值与原始值的对比，可以看出两组数据高度拟合且拟合值满足平滑要求，说明该模型回归方程形式及考虑的影响因素基本合理。当阻尼比为1%时，拟合值与实际值有小幅的偏差，在短周期0.07～0.15 s 尤为明显。图中数据显示：DMF 均值随着阻尼比的增大而减小且随着谱周期的增大，DMF 均值趋向于1，符合长周期时位移反应谱趋于地表最大位移，与阻尼比无关。综上，利用阻尼比对数二次项的回归方程式，对DMF均值有良好的拟合效果。

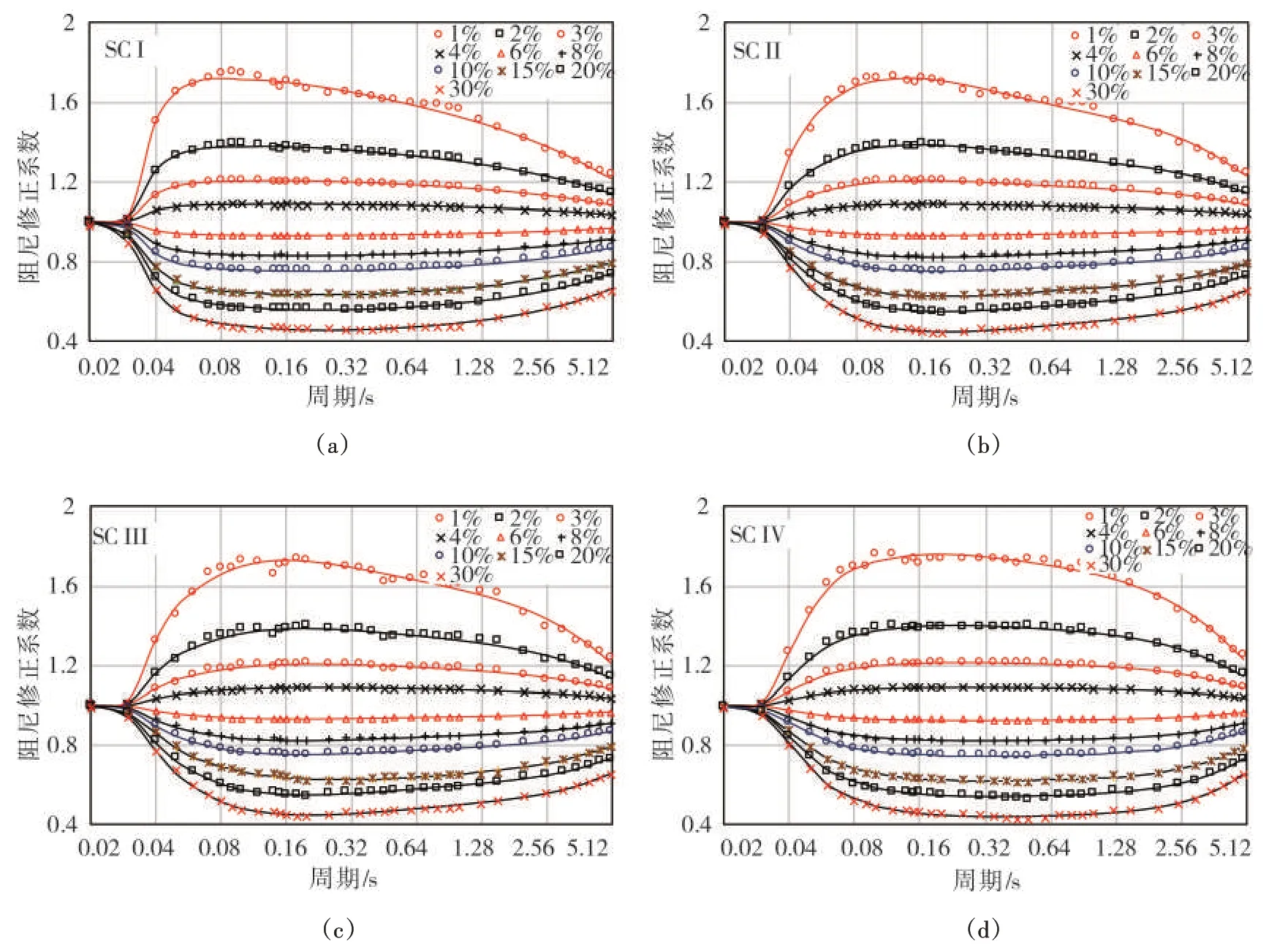
图4 SCI～SCIV拟合DMF值与实际DMF值对比图Fig.4 Comparison ofpredicted values forDMF and actual values for SCI～SCIV sites

3 残差和标准差分析

以上研究发现：该DMF模型的回归效果良好。然而为了对其拟合效果进行更全面的评价并确定误差的来源，必须在此基础上作进一步的残差分析。本文选用ABRAHAMSON 等［37］提出的随机效应方法将残差合理分离，以便在数值方面阐释DMF模型的拟合优度，探究各参数对DMF模型误差的影响。

模型总残差表示为式（6）：

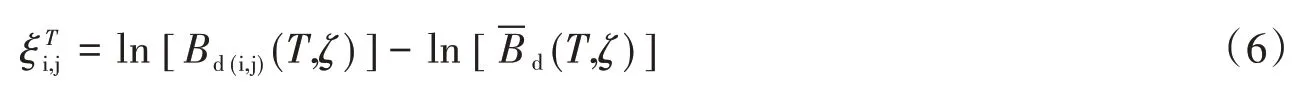
式（6）和式（7）中：i和j分别表示第i次地震事件和第j次记录；表示模型总残差，标准差为σT；ηi表示事件间残差，标准差为τ；ξi,j表示事件内残差，标准差为σ；其各类残差均值都为0。三者标准差有如下关系：

分别给出指定阻尼比与谱周期下事件间残差随震源深度和震级以及事件内残差随震源距离的分布趋势，如图5-6所示。

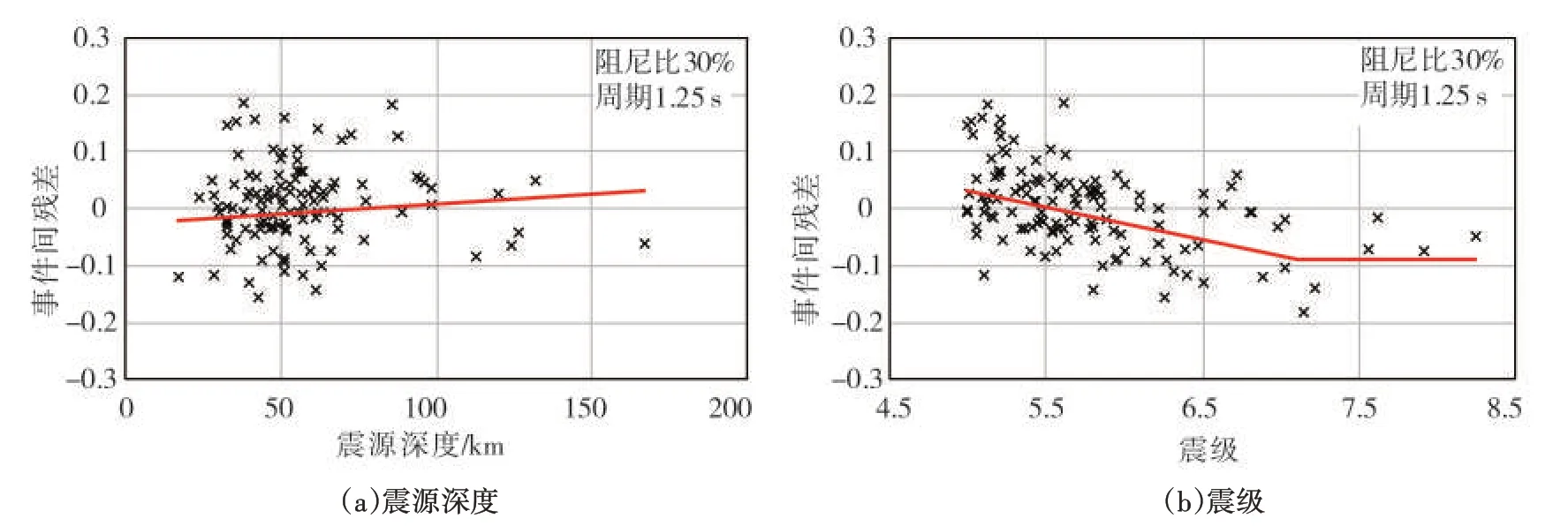
图5 事件间残差随震源深度和震级分布图（周期1.25s，阻尼比30%）Fig.5 Distributions of between-event residuals with respect to focal depth and magnitude（T=1.25s，ζ=30%）

图5（a）可见：事件间残差整体分布于0刻度线附近，趋势线呈现的轻微斜率表明事件间残差与震源深度有一定的相关性；图5（b）采用ZHAO 等［38－39］提出的不同震级标度比率的二段线性模型（取分段点Mw=7.1），可见震级小于7.1 级时其斜率明显，说明事件间残差与震级的相关性比较显著。同理，图6 趋势线呈现的较大斜率说明震源距也是影响DMF 模型的重要因素。综上，加入震级、震源深度和震源距等参数项可以提高DMF 模型的拟合优度，在下一步全参数模型中会有所展现。本文简单模型旨在规范设计反应谱，方便工程应用，没有加入以上相关参数。

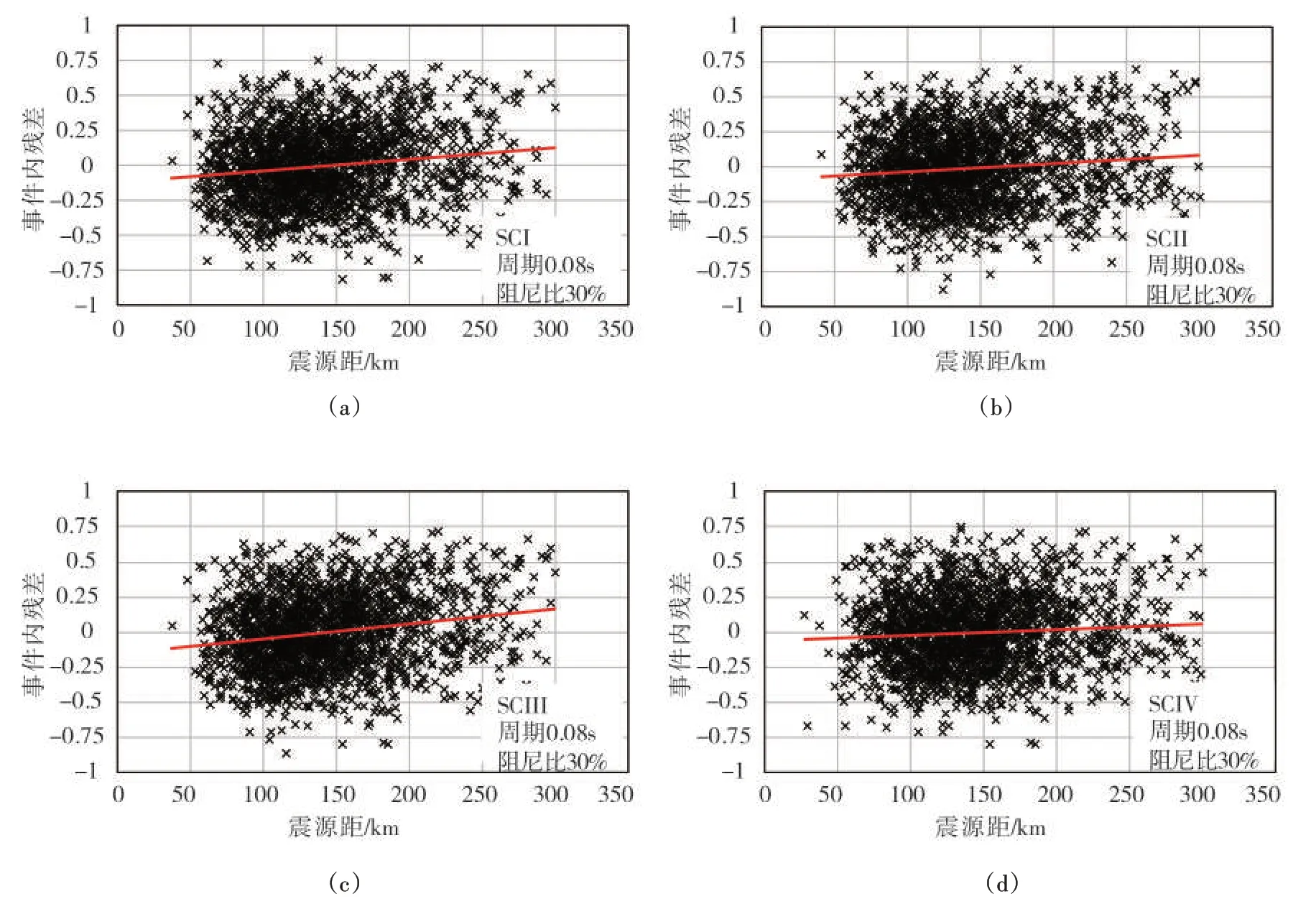
图6 事件内残差随震源距分布图（周期0.08s，阻尼比30%）Fig.6 Distributions of within-event residuals with respect tosourcedistance（T=0.08s，ζ=30%）

给出DMF模型的各类残差标准差的数值，见表5至表7。其中数值大小反映了DMF模型的拟合程度。

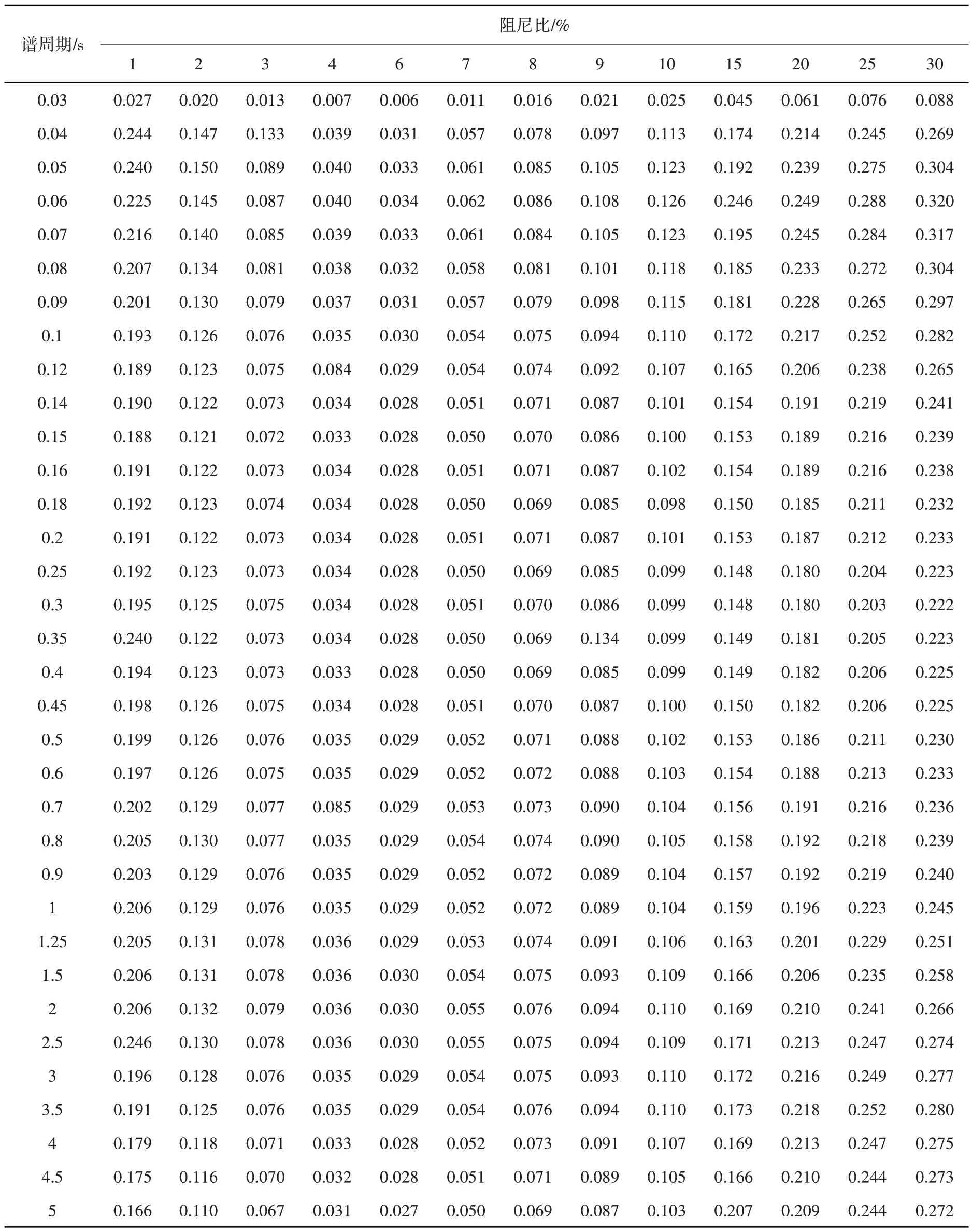
表5 总残差标准差Table 5 Total standard deviations

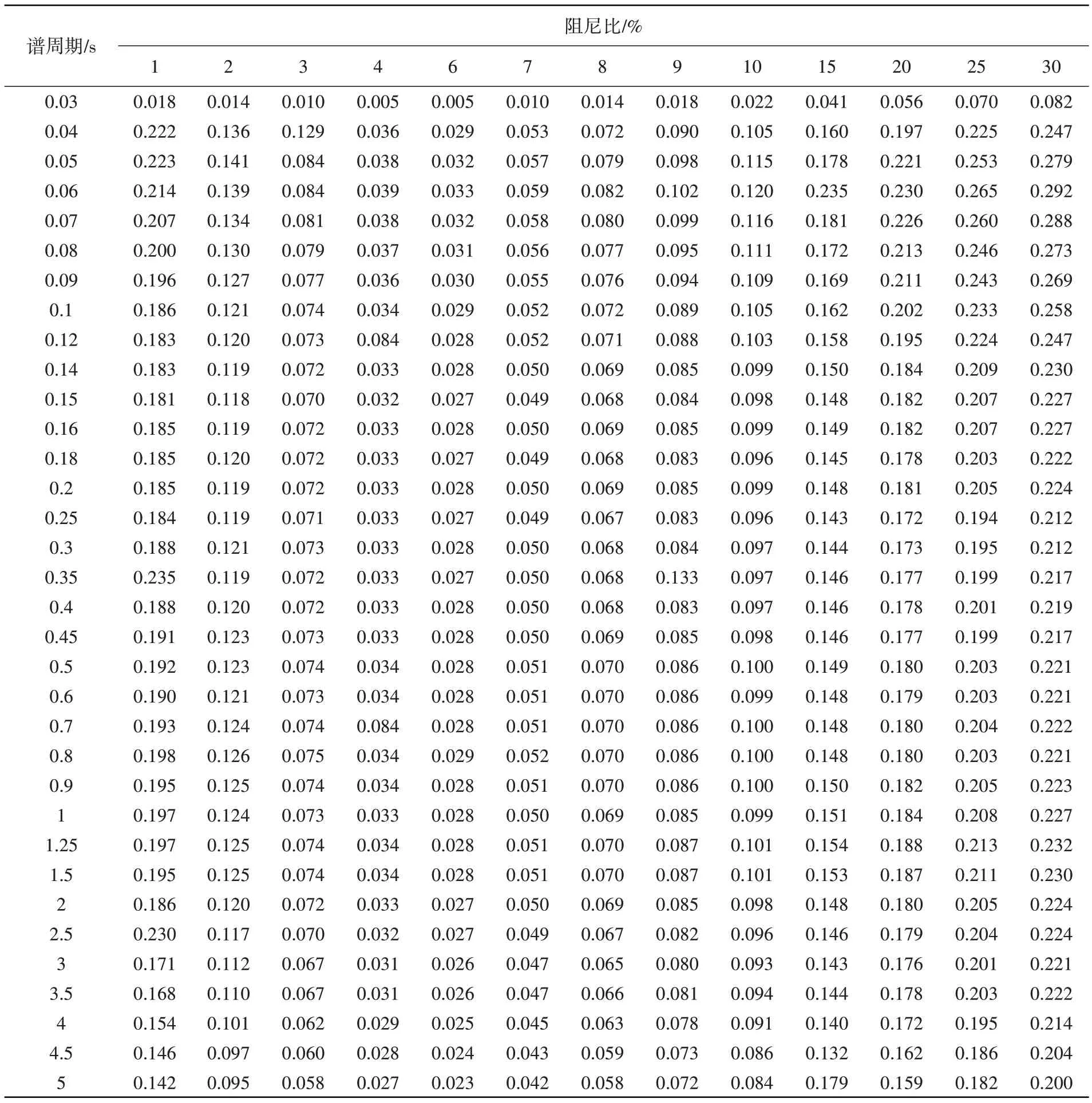
表6 事件内残差标准差Table 6 Within-event standard deviations

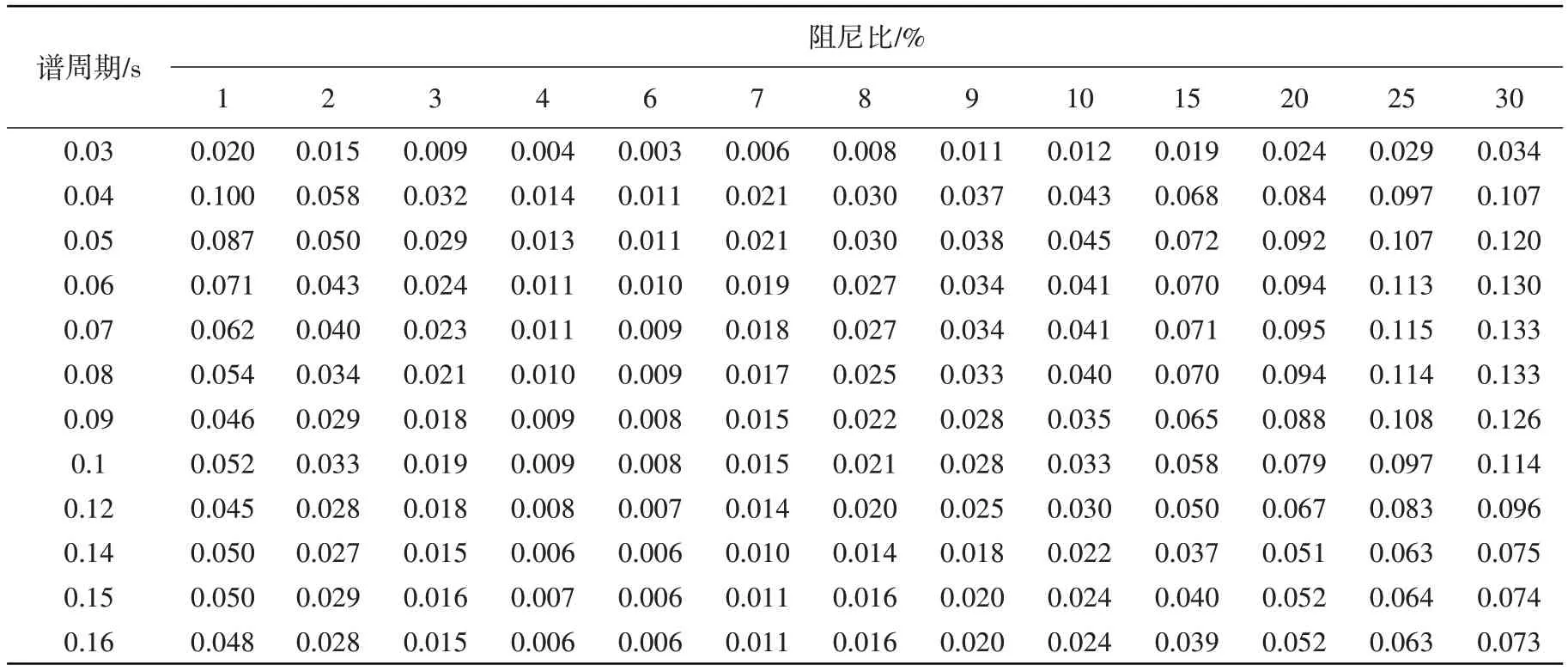
表7 事件间残差标准差Table 7 Between-event standard deviations

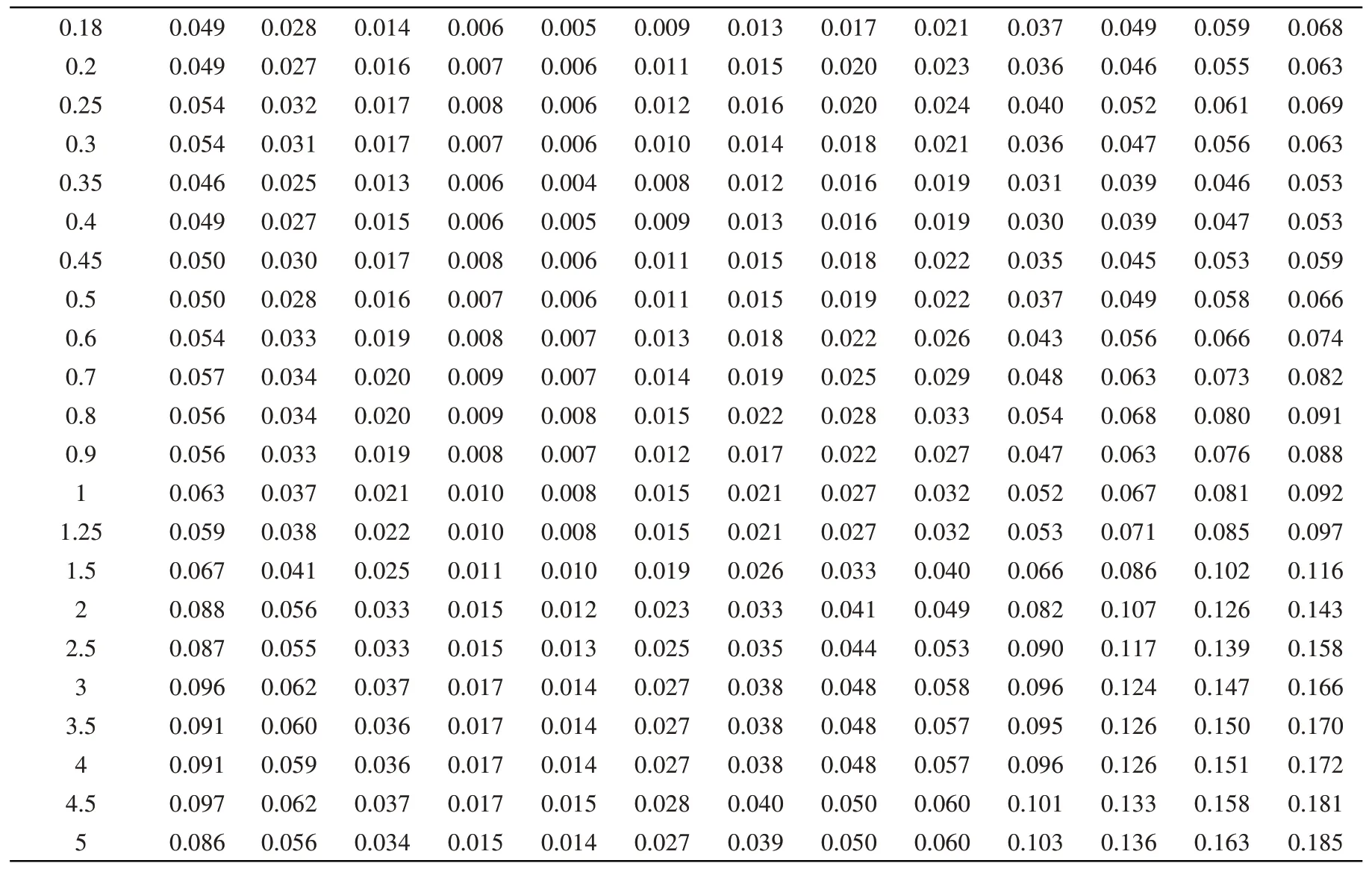
续表

为了更直观的分析DMF 模型各类残差之间的关系，图7 给出了四种阻尼比（ζ=1%、3%、15%和30%）下各类残差标准差随谱周期的分布图。

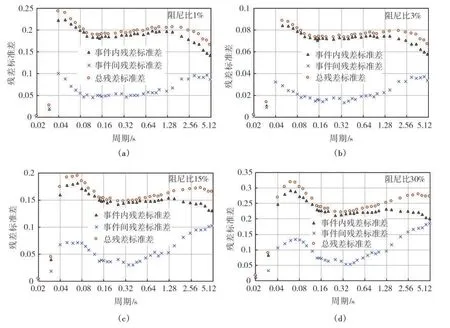
图7 各类残差标准差分布图（阻尼比为1%、3%、15%、30%）Fig.7 Distribution of standard deviations（ζ=1%、3%、15%、30%）

图中可见：（1）事件内与事件间残差标准差趋势基本相同，而事件内残差标准差普遍大于事件间残差标准差，说明场地及路径效应等造成的随机误差大于震源效应造成的随机误差。（2）极短周期（T≤0.02 s）时，事件间残差标准差与事件内残差标准差都为0，长周期（T＞5 s）时，两者逐渐趋于相等。说明在长周期（T＞5 s）时，震源效应与其他效应（路径效应、场地效应）造成的随机误差是近似相等的。

根据随机效应模型进一步将事件内残差分为场地内残差与场地间残差，分别代表了路径效应与场地效应造成的影响。表达式如下：

式中：u和v分别表示第u类场地与第v条地震记录；ξu,v表示事件内残差，标准差为σ；表示场地间残差，标准差为τs；表示场地内残差，标准差为σs；其各类残差均值都为0。

三者标准差有如下关系：

图8 为15%和30%阻尼比水平下SCII 模型标准差随谱周期的分布图。图中可见：（1）场地内残差标准差在多数谱周期上大于场地间与事件间残差标准差，表明路径效应造成的随机误差要大于场地效应与震源效应造成的随机误差。（2）周期小于1.1 s 时，场地间残差标准差大于事件间残差标准差，场地效应造成的随机误差大于震源效应造成的随机误差；1.1 s 之后则相反。（3）由趋势线走向可推断：长周期（T＞5 s）时，场地内残差标准差与事件间残差标准差趋于相等，说明在长周期（T＞5 s）上，路径效应与震源效应造成的随机误差是大致相当的。

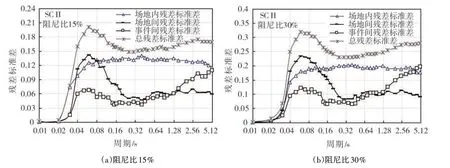
图8 SCII模型残差标准差随谱周期的分布图Fig.8 Distribution of standard deviations with spectral periods for SCII sites

图9 为30%阻尼比下四类场地的场地内残差标准差σs与场地间残差标准差τs的分布图。图中可见：（1）场地内残差标准差在整个周期上普遍大于场地间残差标准差，说明路径效应造成的随机误差占比更大。（2）场地内残差标准差在整个周期上较为相近，主要是因为场地内残差由路径效应引起，理论上与场地类别无关。（3）场地间残差标准差在0.32 s之后有逐渐上升的趋势，说明随着周期的增大，场地效应造成的随机误差越来越大。

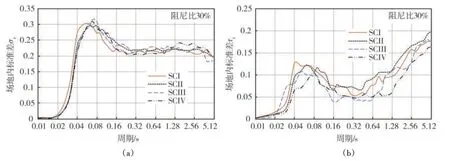
图9 SCI～SCIV场地内、场地间残差标准差随谱周期分布图（阻尼比30%）Fig.9 Distribution of within-site and between-site standard deviations with spectral periods for four site classes（ζ=30%）

最后给出阻尼比为1%与30%时四类场地总残差标准差σT的对比图（图10）。图中可见：（1）任一阻尼比水平下，四类场地标准差曲线的走势基本相同，30%阻尼比下四类场地的标准差普遍大于1%阻尼比下的标准差。（2）短周期（0～0.05 s）时，总标准差随着谱周期的增大而增大；谱周期大于0.05 s 时，总标准差开始减小（拐点周期随阻尼比增大稍有后延），但随着阻尼比的增大有回升趋势。（3）阻尼比为30%时，SCI短周期（0～0.06s）的总残差标准差明显大于其他三类场地。

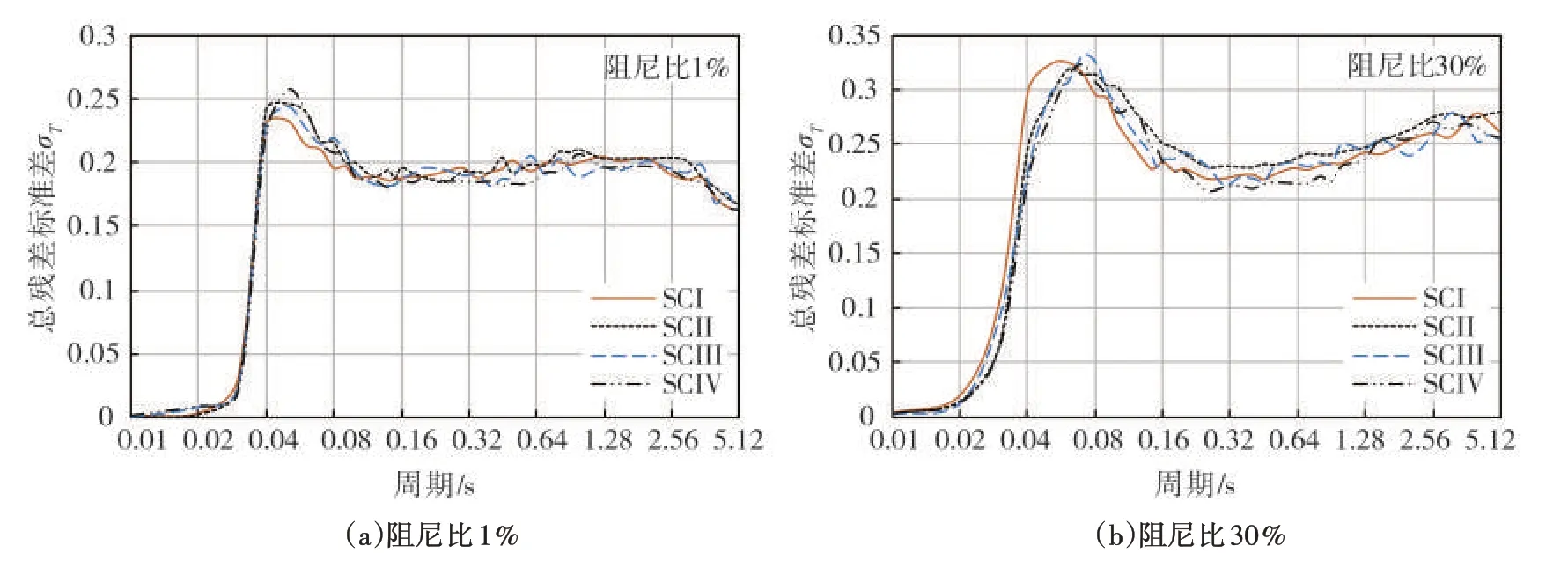
图10 SCI～SCIV总残差标准差随谱周期分布图Fig.10 Distributionof total standard deviations with spectral periods for four site classes

DMF模型的各类标准差都远小于地震动衰减关系相应的标准差，表明各个阻尼比残差纯在统计上部分相关而这些相关部分在计算不同阻尼比反应谱比值时抵消，导致DMF模型标准差较小。

4 结论

基于日本K-NET 和KiK-net 台网中4 695 条俯冲带板内地震记录的竖向分量，建立了考虑场地类别、谱周期以及阻尼比的位移谱DMF模型。通过随机效应模型将模型总残差分为事件间和事件内残差，进一步将事件内残差分为场地间及场地内残差，来探究各参数对DMF模型随机误差的影响。主要结论如下：

（1）利用阻尼比对数二次项的回归方程式，对DMF均值有良好的拟合效果。

（2）Z检验结果表明：不同场地类型对DMF 均值的影响程度显著，分场地来建立DMF 均值模型是必要的。

（3）通过随机效应模型对残差的分析可知：事件间残差与事件内残差分别和震级、震源深度与震源距相关。加入震级、震源深度和震源距等参数项可以提高DMF模型的拟合优度。后续研究会据此对模型作进一步的完善。

（4）纵观全周期，路径效应造成的误差占比相对更大；周期小于1.1 s 时，场地间残差标准差大于事件间残差标准差，场地效应造成的误差大于震源效应造成的误差，1.1 s后则相反；长周期（T＞5 s）上，路径效应与震源效应造成的随机误差大致相当；随着谱周期的增大，场地效应造成的随机误差越来越大。

（5）本文建立的DMF模型利用俯冲带板内地震数据，可为我国台湾及南海地区的抗震设计提供参考。