基于卷积神经网络的地震预警震级持续估算方法研究

江炳根，马 强，陶冬旺

（1.中国地震局工程力学研究所，黑龙江哈尔滨 150080；2.中国地震局地震工程与工程振动重点实验室，黑龙江哈尔滨 150080）

引言

地震预警可以在破坏性地震波到达前向预警目标区发布预警信息并启动地震应急控制系统，减少伤亡损失及消除潜在威胁等，是我国近年来针对地震自然灾害大力发展的一种防灾减灾手段。

预警震级的快速估算是地震预警中的重要环节，其震级估算结果将极大影响预警信息的时效性与准确性。目前在国内外地震预警系统的实际研究应用中，震级快速估算方法主要是基于地震台站检测到地震P波到达后数秒内的特征参数与震级的统计回归。现行的预警特征参数主要分为周期类参数、幅值类参数以及能量强度参数，其中周期类参数τc与幅值类参数Pd在地震预警系统中应用最为广泛。在NAKAMURA 研究得出的使用卓越周期估算震级这一方法的基础上［1－4］，ALLEN 等［5］和KANAMORI6］对此开展了进一步研究，通过计算P 波触发后3～4 s 内的平均特征周期τc来进行震级估算；金星等［7］、WANG 等［8］和PENG 等［9］基于τc参数也都进行了震级估算研究。目前τc参数在多个国家和地区的地震预警系统中都得到了应用；WU等［10－11］利用美国加州地区地震数据，将采用滤波后的位移记录中P波触发3 s时间内的位移幅值Pd与震级进行统计拟合，结果表明两者之间具有较好的线性关系；此后，ZELLO 等［12］和PENG 等［13］等对该方法进行了发展。目前，Pd参数已是地震预警系统中最常用的参数。

大地震发生过程中，在部分近源台站监测到地震P 波到达后，发震断层仍处于破裂状态，震源附近台站可以持续接收更多的地震波信息，远源台站也会持续触发，因此后续的地震预警信息更新需要地震预警系统具有震级持续估算能力。此外，传统基于P 波3 s 固定时间窗的方法在对6.5 级以上大震进行处理时普遍存在震级饱和现象，而采用震级持续估算模式有助于改善这一问题［14］。WU 等（2006）、KANAMORI 等（2005）和王延伟等［15］等使用单参数震级回归方法，通过延长时间窗，在P 波触发后4 s、5 s、…、10s 时间窗分别建立对应的回归模型，实现了对震级的持续估算，有效改善了大震震级低估问题，提高了估算结果的准确性。

但目前的地震预警系统中基于单参数的震级快速估算方法，都是基于P 波到达后3～4 s 内地震波的幅值或者频率、周期等单一特征参数，单参数方法的不确定性较大，必然会出现震级估算结果离散性较大和准确性不高等问题，而通过使用多参数则可以充分利用更多的地震波信息，提高震级估算的准确性。深度学习是一种人工智能中的机器学习算法，其能够从输入的样本数据原始特征中提取更加复杂的特征加以学习应用，以期获取较好的目标结果。卷积神经网络算法是目前深度学习领域最常使用的算法，通过参考生物复杂的神经网络运转流程，通过对数据的局部感知以及各神经网络层之间的权值共享，其可以大大降低模型的待估计权值数量，作为一种高效的算法，通过将庞大数量的原始数据通过卷积池化进行降维处理，从而提升模型泛化能力和训练效率［16］，目前已广泛应用于地震科学研究中，MOUSAVI等［17］和MEIER等［18］都使用卷积神经网络算法在震级估算等领域取得了众多成果。

马强［19］、胡安东等［20］和朱景宝等［21］基于机器学习理论中的神经网络算法（Artificial Neural Network，ANN）和支持向量机算法（Support Vector Machine，SVM）使用多参数以快速估算地震预警震级，MEIER 等（2019）和ZHANG 等［22］通过使用卷积神经网络算法（Convolutional Neural Network，CNN）建立多参数震级回归模型，延长时间窗获取更多地震特征信息，实现震级持续估算，从而有效提高了震级估算的准确性，取得了较好的震级持续估算效果。

为了提高地震预警震级持续估算准确性，本文利用日本KiK-net 强震台网记录到的地震记录井下三分量数据共50 424组，在P波触发后3～10 s时间窗内选取幅值参数、周期参数、烈度参数及信噪比参数四大类共11种特征参数以及震中距信息，构建了基于CNN卷积神经网络的震级估算模型（Convolutional Neural Networksfor earthquake magnitude estimation，CNN-M），并选取2014 年长野Mj6.7 级地震和2021 年宫城Mj6.9 级地震用作开展线下分析，旨在探索地震预警震级持续估算的新途径，以便为“国家地震烈度速报与预警工程”项目的建设提供震级估算方法参考。

1 CNN-M模型介绍

基于卷积神经网络这一深度学习算法，构建CNN-M 模型使用台站记录的全三分量信息，选用了共计11种地震动特征参数，以期望得到不同分量地震动特征参数组合与震级的关系。将各时间窗内的三分量特征参数转化为二维张量作为模型输入，预估的震级结果作为模型输出。整个CNN-M 模型共12层神经网络，除去首尾的输入、输出层外共设置了9个隐藏层，其中Conv1层使用了64个卷积核，Conv2层使用了128个卷积核，在卷积层和池化层逐层特征提取与过滤后，再连接上五层全连接层，每层全连接层都使用ReLU 函数作为激活函数。此外，根据HINTON［23］和KRIZHEVSKY［24］的相关研究，在第2池化层与第1全连接层之间加入了一层Dropout层，用以防止出现过拟合现象，同时加快有效训练速率。

模型架构如图1 所示，共有大约135 万个待估计参数，根据KRIZHEVSKY（2012）的研究表明：本文共使用了5万条强震动数据，可以完成对CNN-M模型的有效训练和测试。

2 数据选取及处理

2.1 数据选取

本文所使用的强震动记录全部来自于日本防灾科学研究所（NIED，National Research Institute for Earth Science and Disaster Prevention）的KiK-net数据库，并基于以下原则对数据进行筛选：

⑴震源位置：日本陆地或陆地沿岸近海；

⑵震级范围：Mj3.0～Mj9.0；

⑶震源深度：≤50 km；

⑷台站震中距：≤150 km。

考虑到Mj6.5级以上大震数据量偏少，故对Mj6.5级以上大震数据的震中距不做限制。

基于以上原则，共筛选出5 713 次地震，所记录的强震数据共50 424 组，记录到地震动记录台站697 个，井下三分量数据151 272条。图2展示了本文选用数据集的震中位置分布和台站位置分布。

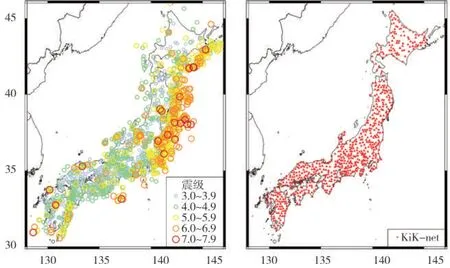
图2 强震数据记录的震中及KiK-net台站分布Fig.2 Location of the epicenters and KiK-net station based on strong ground motion records

按照7：3的比例，将筛选得到的50 424组数据随机划分成训练数据集35 297组与测试数据集15 127组，对应的地震震中位置、震级和台站位置都来自于KiK-net数据库中的强震动观测目录。在此之外，单独使用了2014年11月22日长野Mj6.7级地震数据和2021年3月20日日本宫城县Mj6.9级地震数据进行震例分析。

图3展示了训练集和测试集的震级、震源距和强震记录数量关系。

图3 KiK-net数据记录震级及震源距分布Fig.3 Distribution ofthedatafromKiK-net showsthenumberof magnitude and hypocentral distance

2.2 数据处理

本文对选取的数据做如下处理：

（1）使用马强等［25］提出的自动捡拾方法对强震数据的P波震相自动识别捡拾，通过人工二次审核以确认准确性并手动修改捡拾错误情况；

（2）采用四阶0.075 Hz高通巴特沃斯（Butterworth）滤波器对原始强震记录进行滤波处理，以便有效消除后续积分过程中出现的低频漂移现象。在此基础上，针对滤波后的强震记录加速度数据通过多次积分分别得到对应的速度和位移记录；

（3）为提升CNN模型的训练效率和训练精度，对输入模型的多特征参数值进行了标准差标准化处理，使得数据的均值为0，标准差为1。

2.3 地震动特征参数

选取了幅值类参数、周期类参数以及烈度参数三大类共计11种地震动特征参数，计算KiK-net强震台网数据P波触发后3～10s各时间窗的特征参数用以CNN-M模型训练和测试使用。

（1）幅值参数

位移幅值Pd：WU等研究了使用原始加速度记录滤波后通过积分得到的3 s时间窗内的位移与震级的相关回归关系，即为“Pd方法”，其中：P（dcm）即为P波触发后计算时间窗内的位移绝对值的最大值，计算方法如下：

加速度幅值Pa：对应Pd参数定义，即为所选用时间窗内加速度绝对值的最大值，单位gal。

速度幅值Pv：对应Pd参数定义，即为所选用时间窗内的速度绝对值的最大值，单位cm/s。

（2）周期参数

特征周期τc：KANAMORI 在NAKAMURA 提出的卓越周期参数的基础上进行了改进，提出了依据P 波触发后3～4 s时间窗来计算特征周期τc，进而估算震级，计算方法如下：

式中：v（t）为速度时程；d（t）为位移时程。

构造参数TP：在WU 等提出的幅值参数Pd和KANAMORI 等提出的特征周期τc的基础上，通过进一步研究，HUANG 将两者乘积作为震级估算参数，即为构造参数TP，通过研究分析论证了其与震级之间存在的较强回归相关性［26］，计算方法如下：

峰值比Tva：KRAMER 通过计算Pv与Pa的比值，发现其可有效反应所选用时间窗内的地震动的时程频率成分［27］，其计算方法如下：

（3）烈度参数

破坏烈度DE：NAKAMURA 提出累计能量变化率DI（Destructive Intensity），DI综合考虑加速度（gal）和速度（cm/s）对于地震破坏间的相关关系，体现了地震三要素幅值、频谱和持时的影响，对DI 取最大值则为DE［28］，其计算方法如下

式中：a为加速度时程；v为速度时程。

累积绝对速度CAV：通过计算速度绝对值在时间窗内的累计结果，作为烈度参数，其即可以反应地震三要素，亦可有效反应地震动能量强度，该参数由美国电力研究所EPRI（1988）提出［29］，单位cm/s，其计算方法如下：

式中：T为选用的时间窗长度；a（t）为加速度时程。

均方根加速度arms：单位gal，其计算方法如下［30－31］：

持续加速度峰值PGAc［32］：单位gal，其计算方法如下：

式中：amax为加速度时程峰值；ai为加速度时程中最大的十个幅值。

（4）信噪比参数

信噪比：定义SNR 为台站触发后各时间窗内原始加速度记录均方根幅值与触发前的噪声均方根幅值之比，可有效反映记录的可靠程度［33］，计算式如下：

3 结果

定义估算震级与实测震级之差为误差xi=yi-，其中：yi为实测震级，为估算值，并计算数据集的标准差σ，如下式：

式中：xi为实测震级均值；为误差均值。

3.1 震中距效应对震级估算结果的影响

在CNN-M 模型输入端，输入地震波特征参数11种以及强震记录的方向，以模型估算震级作为输出。在地震台站P 波触发后较短时间窗内，震中距的估算精确与否对各种震级估算方法都有很大的影响，在MEIER等（2015）和YIN等［34］的研究中表明：添加了震中距信息可有效加强各自研究中卷积神经网络模型的适用性和估算结果的准确性。

为验证震中距对CNN-M模型的影响，以相同的神经网络架构，使用井下台站数据作为训练集及测试集，分别在有震中距参数输入和无震中距参数输入的情况下，进行模型的训练与测试。表1 展示了P 波触发后3～10 s时间窗内，以1 s为间隔来计算各时间窗内在有无震中距参数CNN-M 模型时基于训练数据集以及测试数据集的标准差统计结果。

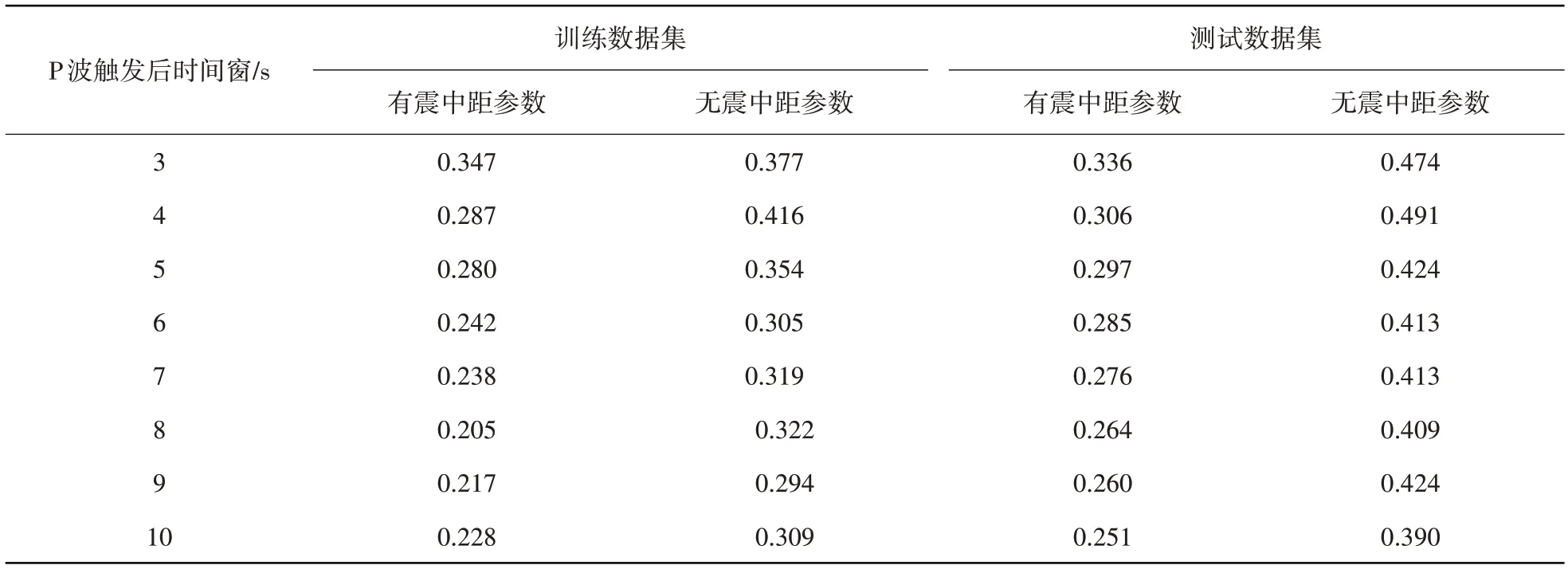
表1 有无震中距参数时CNN-M模型震级估算结果标准差Table 1 Standard deviation of CNN-M model estimating magnitude with the epicenter distance parameters andwithout epicenter distance parameters

图4（a）和图4（b）中的离散点展示了同表1相同的数据，离散点连线表示训练结果的标准差随时间窗的变化规律。

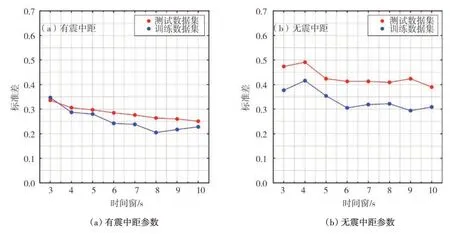
图4 CNN-M模型估算震级的误差标准差Fig.4 Standard deviation of CNN-M model estimating magnitude

通过图4 中展示的数据对比可知：在有震中距参数输入的前提下，相较于无震中距参数输入时，其训练集和测试集的标准差都有了明显减小，各时间窗内训练集标准差平均降低0.082，测试集标准差平均降低0.145，且在有震中距参数输入时，测试集和训练集的标准差更为接近，说明此时模型的泛化能力更强。在我们重点关注的测试集数据中，在有震中距参数输入的前提下，3 s 时间窗时标准差为0.336，10 s 时间窗时降低为0.251，表明CNN-M模型已经取得了较为优秀的震级估算效果。

分析结果表明：震中距参数对于模型的训练是十分重要的。考虑到日本KiK-net 强震台网的台站分布非常密集，在监测到地震发生后，可以利用多台联合震中定位技术来实现对震中距的快速准确计算，因此将震中距作为已知参数输入模型可以有效增强模型的估算效果。

小伊发觉到自己的双重人格时，正骑着已经被禁止的无牌照摩托车穿越在寂静的市中心，播放出的聒噪摇滚乐引来了巡逻民警，小伊熟练地把速度换到最高档位，享受着摆脱追逐的快感，转弯的瞬间离心力在地上蹭出一条划痕，眼角根据角度的变换在无意中瞥到了什么建筑，他还没有明白对这栋建筑的熟悉感来自哪里，大脑就已经传来阵痛，愈演愈烈，在从摩托车飞出的瞬间，他恍惚想起这似乎是个学校，桌椅已经老旧，上面写满了少男少女的笔迹。摔在地上的那一刻，小伊感到似乎有什么重要的东西从他身体里流出。

3.2 场地效应对震级估算结果的影响

日本的KiK-net台站，在地震发生时可同时记录井下基岩部分传感器数据和井上土层部分传感器数据，在KOKUSHO等［35］的研究中，表明不同地区的场地效应，会造成其台站井上记录相较于井下记录存在放大效应。为验证井上井下之间的场地放大效应对CNN-M 模型的影响，我们使用井上台站的强震动记录数据，添加震中距参数，输入到本文的模型中进行模型的训练和测试。表2展示了基于井上数据的P波触发后3～10 s各时间窗内CNN-M模型训练数据集以及测试数据集的标准差统计结果。

表2 有震中距参数时井上数据CNN-M模型震级估算结果标准差Table 2 Standard deviation of CNN-M model estimating magnitude by using the surface station record with the epicenter distance parameter

图5展示了在添加震中距参数前提下，井上记录和井下记录使用CNN-M 模型的训练集误差标准差和测试集误差标准差随时间的变化关系。通过对比使用井上数据和井下数据时模型在训练数据集和测试数据集上的震级估算结果标准差，可以发现使用井上数据时，其标准差普遍偏大，各时间窗内训练集标准差平均偏大0.044震级单位，测试集标准差平均偏大0.089震级单位。

图5 有震中距参数时CNN-M模型震级估算结果标准差Fig.5 Standard deviation of the CNN-M model for estimating magnitude with the epicenter distance parameter

综合上述研究对比分析，使用添加震中距参数的井下数据可以使模型得到最佳效果，因此本文的CNN-M模型训练以及后续的研究分析都将使用添加震中距参数的井下数据。

3.3 震级估算结果对比分析

图6-7 分别为P 波触发后3～10 s 时间窗内的CNN-M 模型的训练数据集震级估算结果和测试数据集震级估算结果。两图中，黑色实线表示模型估算震级与实际震级1：1线性比例关系，两条虚线表示该时间窗下震级估算结果±1倍标准差。

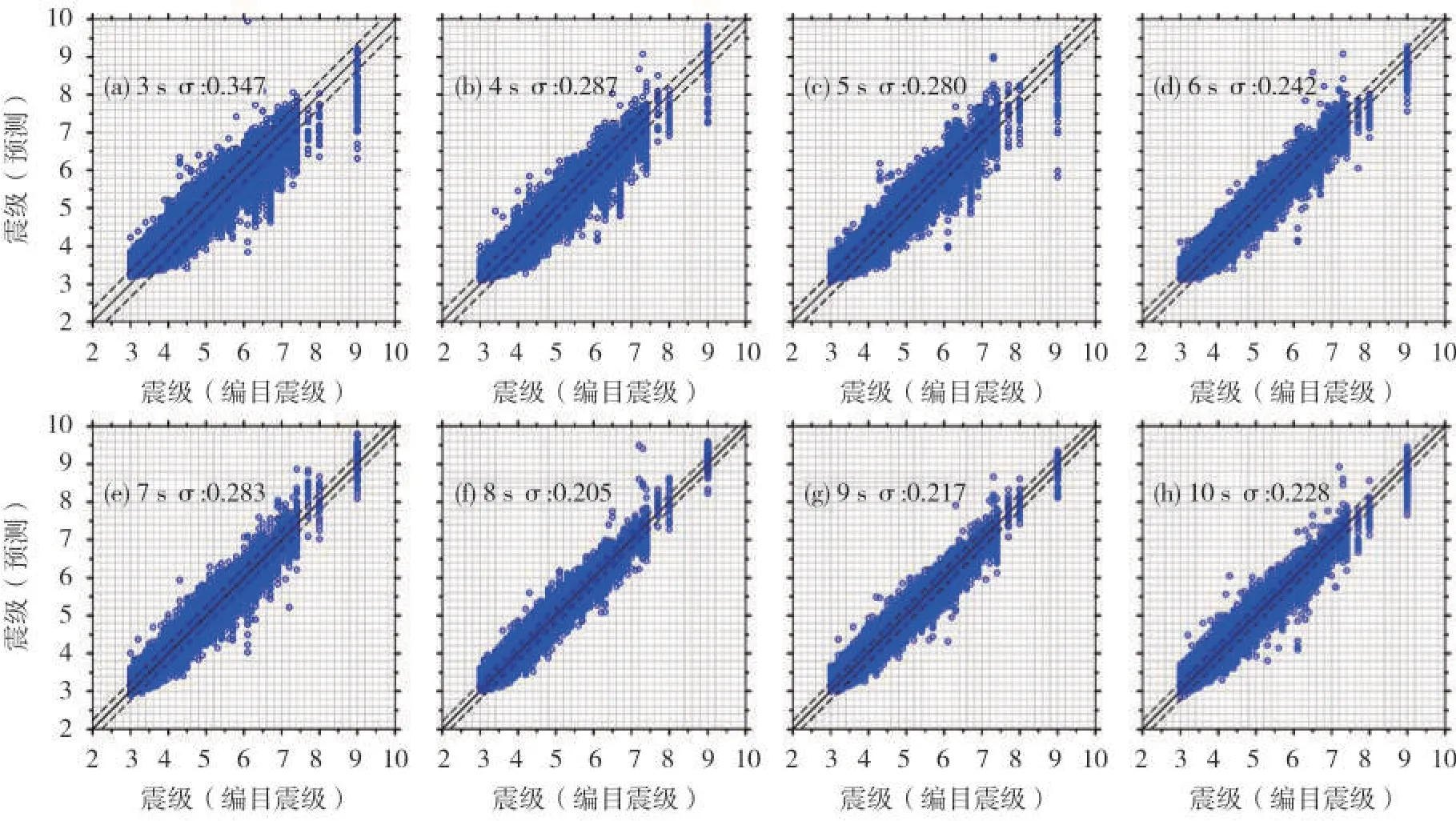
图6 P波触发后3～10s时间窗CNN-M模型训练结果Fig.6 Magnitude estimation results of the CNN-M model based on the training set in the time window of 3～10 s after the P wave arrivals

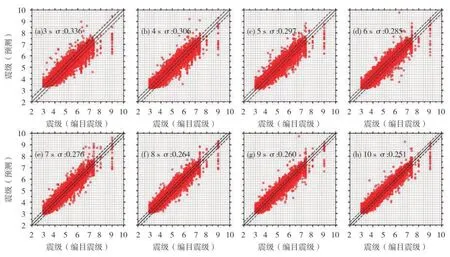
图7 P波触发后3～10s时间窗CNN-M模型测试结果Fig.7 Magnitude estimation results of the CNN-M model based on the testing set in the time window of 3～10 s after the P wave arrivals

通过图6-7，我们可以更直观看出随着时间窗的增大，无论是训练集还是测试集，CNN-M 模型都输出了更为稳定可靠的震级估算结果，具体表现为误差降低，震级回归估算结果离散性减小，大震低估现象逐步改善。在图6-7 的基础上对P 波触发后3～10 s 时间窗CNN-M 模型的训练集结果和测试集结果进行了误差分析统计，对应的CNN-M 模型训练数据集结果的误差频数分布和测试数据集结果的误差频数分布分别如图8-9所示。

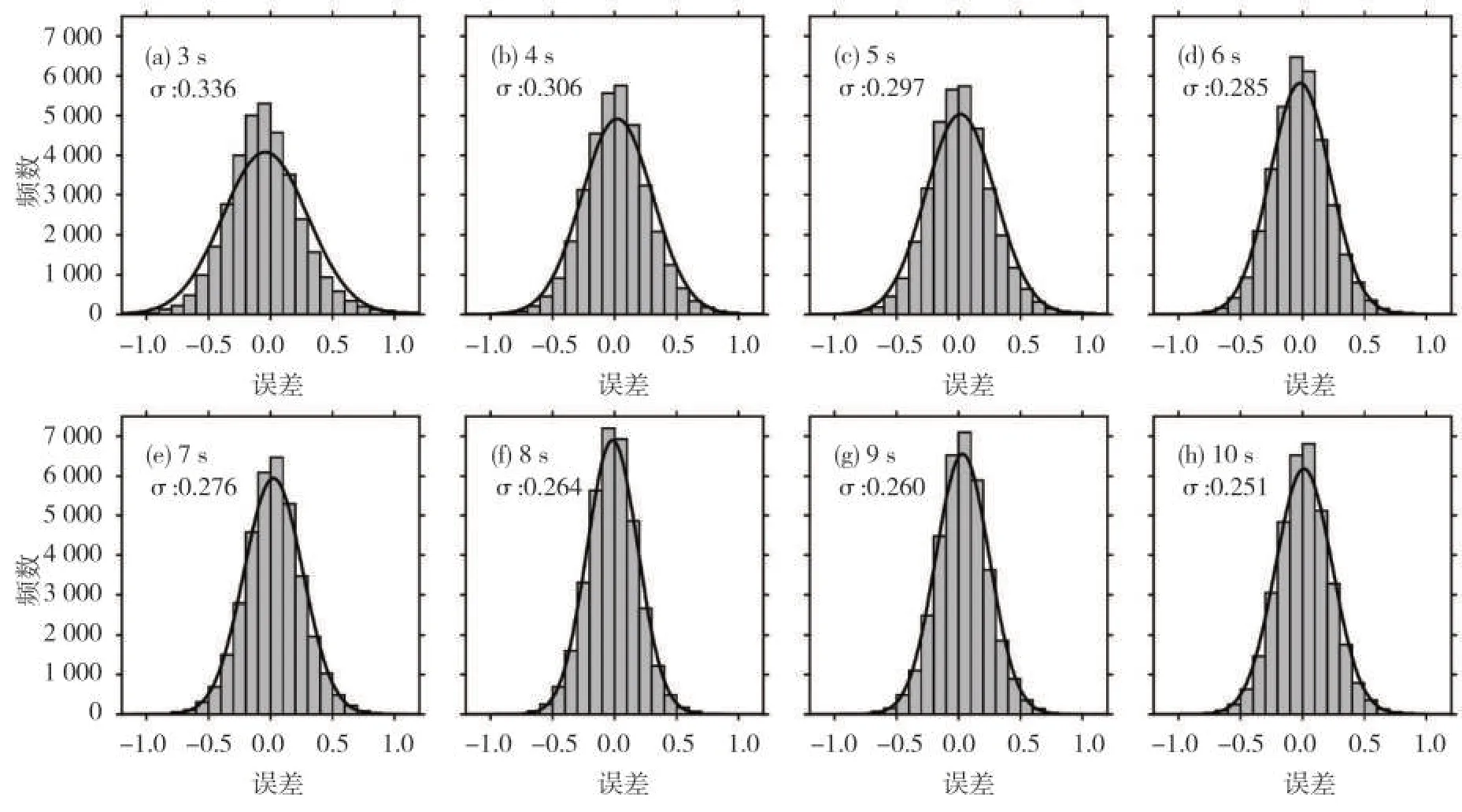
图8 P波触发后3～10s时间窗训练集误差直方图Fig.8 Error histogram of the CNN-M model based on the training data set in the 3～10 s time window after the P wave arrivals

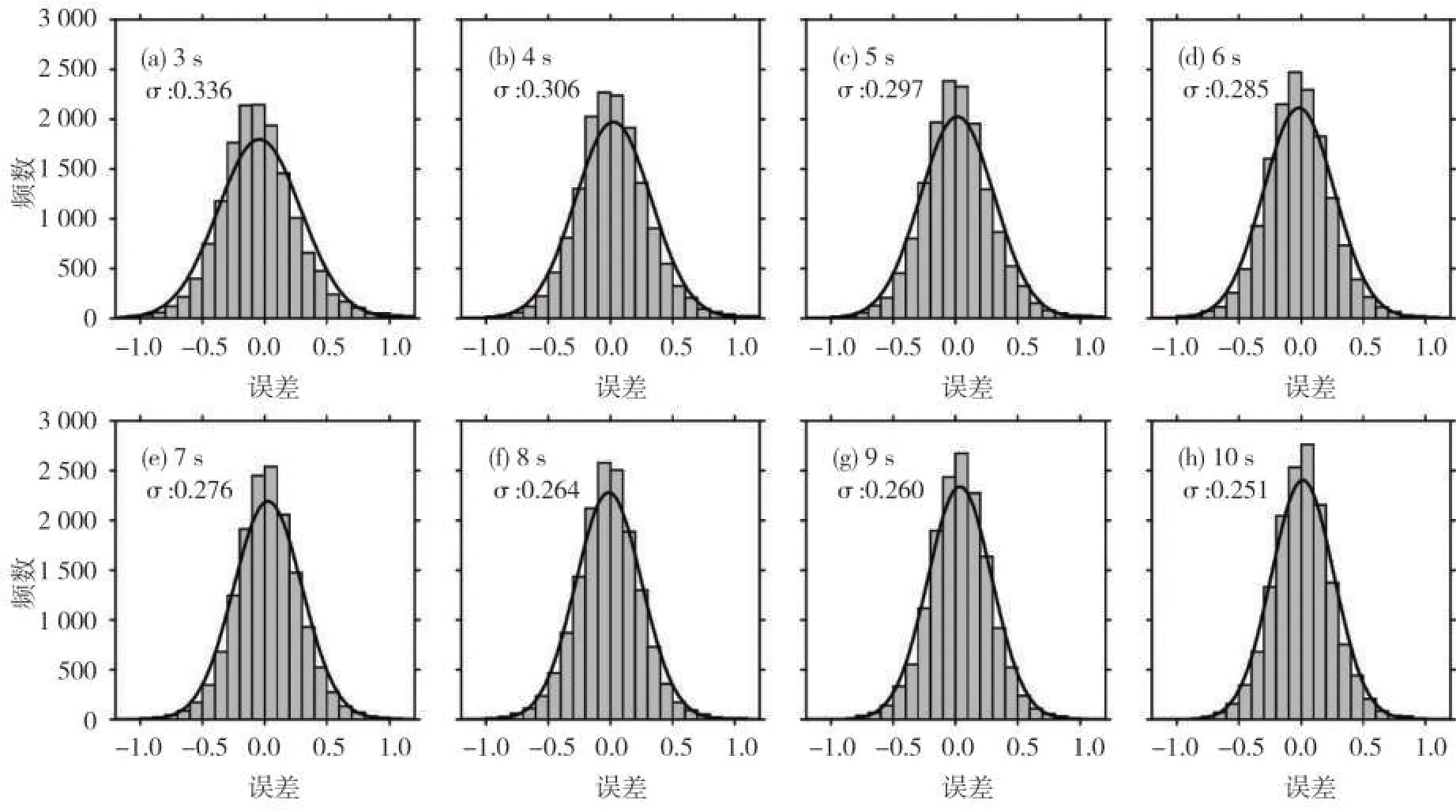
图9 P波触发后3～10s时间窗测试集误差直方图Fig.9 Error histogram of the CNN-M model based on the test data set in the 3～10 s time window after the P wave arrivals

通过误差直方图、直方图平滑曲线以及标注的标准差可以看出：无论是训练集结果还是测试集结果，误差分布都呈正态分布趋势，且随着时间窗的增大，标准差逐渐降低，其中我们重点关注的测试集数据震级估算结果误差在0.50 震级单位范围内的占比由89.3%逐步增加到95.4%，说明CNN-M 模型具有准确稳定的连续震级快速估算能力。

使用同样的测试集数据，参考WU（2005）等使用对美国南加州地区震级回归拟合所用方法和公式，图10展示了使用训练数据集进行拟合得到Pd方法公式来对测试数据集进行震级估算结果，将其与CNN-M模型在测试集下的结果进行对比可以发现：在同样的数据集下，“Pd方法”较之CNN-M 模型有较大差距，其各个时间段内的标准差普遍在0.4 左右，而CNN-M 模型在5 s 时间窗时误差便降低至0.3 以内，说明CNN-M 模型具有了更为可靠的快速估算能力；“Pd方法”亦存在短时间窗内的大震明显低估现象，MURPHY 等［36］认为对于大震级事件仅利用P波触发后3 s信息进行地震预警时，由于对断层破裂过程欠采样，因此无法反映整个破裂断层的规模，存在饱和震级6.5 级。虽然随着时间窗的增大该低估现象会有一定改善，但受限于其他条件，始终无法做到对大震的准确估计，而CNN-M 模型则不同，在对大地震进行处理时也具有一定的快速准确估算能力。

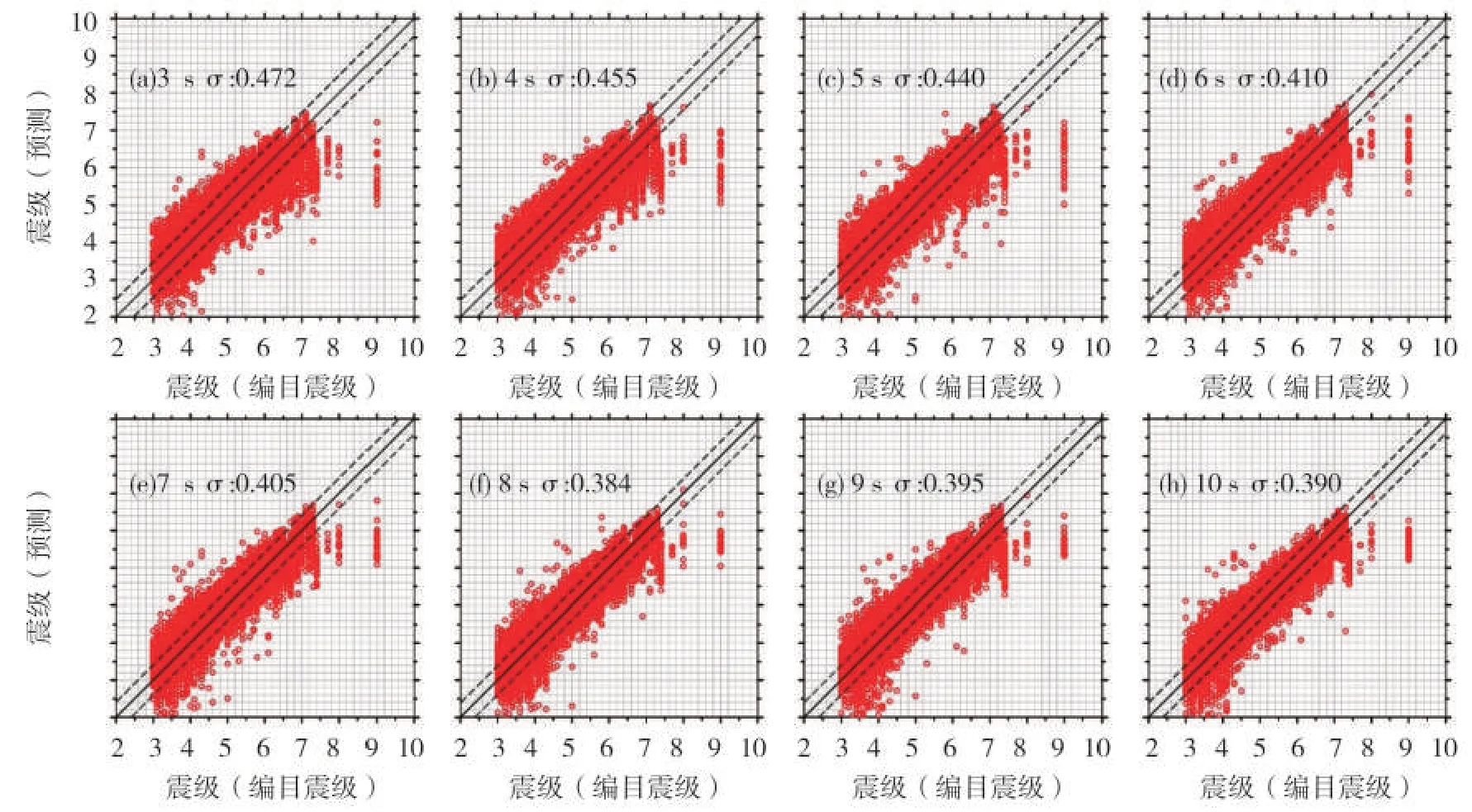
图10 P波触发后3～10s时间窗“Pd方法”震级估算结果Fig.10 Magnitude estimation results based on the"Pd method"in the time window of 3～10 s after the P wave arrivals

4 震例分析

为验证CNN-M 震级估算模型在对大地震进行处理时的实际震级估算效果，选取2014年11月22日日本长野县Mj6.7 级地震和2021 年3 月20 日日本宫城县Mj6.9 级地震作为震例进行单独分析。对于两次地震震例，使用KiK-net强震台网记录到的井下三分量记录，通过人工捡拾确定P波到时，其中长野地震共135组记录，宫城地震共141组记录。两次地震震中以及记录到数据的台站位置分布如图11所示，图11（a）中红色圆圈为震中近场100 km范围圈，共有36个台站位于此范围圈内；图11（b）中红色圆圈为地震波触发首台后10 s内总共触发的22个台站，震中距最远为105.45 km。

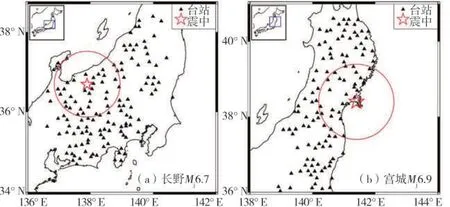
图11 长野Mj6.7级和宫城Mj6.9级地震震中及台站分布图Fig.11 Distribution of epicenter and stations of Nagano-ken Mj 6.7 earthquake and MiYagi Mj 6.9 earthquake

4.1 长野Mj6.7级地震震级估算结果分析

长野Mj6.7 级地震震源深度5 km，属于浅源地震。图12 显示了利用CNN-M 模型和单台站记录对P 波触发后3～10 s 各时间窗内长野地震进行震级估算的结果，图12（a）为震中距100 km 范围内的36 个近场台站记录的估算震级结果，图12（b）为震中距大于100 km 的99 个远场台站记录的估算震级结果，图中黑线为实际震级Mj6.7级，各子图中标注的σ为估算震级相对实际震级的误差标准差。

从图12（a）中可以看到在P波触发3 s后，近场部分台站已经成功估算出实测震级，即可发出地震预警信息，但有些台站仍然低估。而随着时间窗的增大，台站记录所包含的地震信息开始丰富起来，近场台站记录的震级估算结果误差逐渐减小，估算结果离散性降低，有更多的台站可以准确估算出实际震级。

在图12（b）远场台站估算结果中，3 s时间窗时震级估算离散性较大，大震级低估现象始终存在，但仍有一部分台站可以准确估算出实际震级。而随着时间窗的增大，震级估算结果离散性开始变小，误差同步减小，99个远场台站的估算结果也开始和实际震级接近，说明本模型具有较强的异地预警能力。

4.2 宫城Mj6.9级地震震级估算结果分析

在2021年3月20日，日本宫城县附近海域发生地震，震中位于宫城县近海，日本气象厅速报结果为Mj7.2级，震源深度60 km，后续日本气象厅修正震级为Mj6.9 级，震源深度为59 km，属于中源地震，未对日本境内造成重大伤亡。

图13展示了CNN-M 模型使用单台站记录来对P波触发后3～10 s各时间窗内宫城地震进行震级估算的结果，图中黑线为实际震级Mj6.9级，各子图中标注的σ为估算震级相对实际震级的标准差。对于此次地震，CNN-M 模型在使用3 s 和4 s 时间窗时，估算结果仍旧存在明显的近场台站数据震级低估现象，误差离散性也较大，但随着时间窗的增长，近场台站的估算结果逐渐接近真实震级，远场台站的估算结果则相对比较稳定，没有出现明显的震级低估现象。

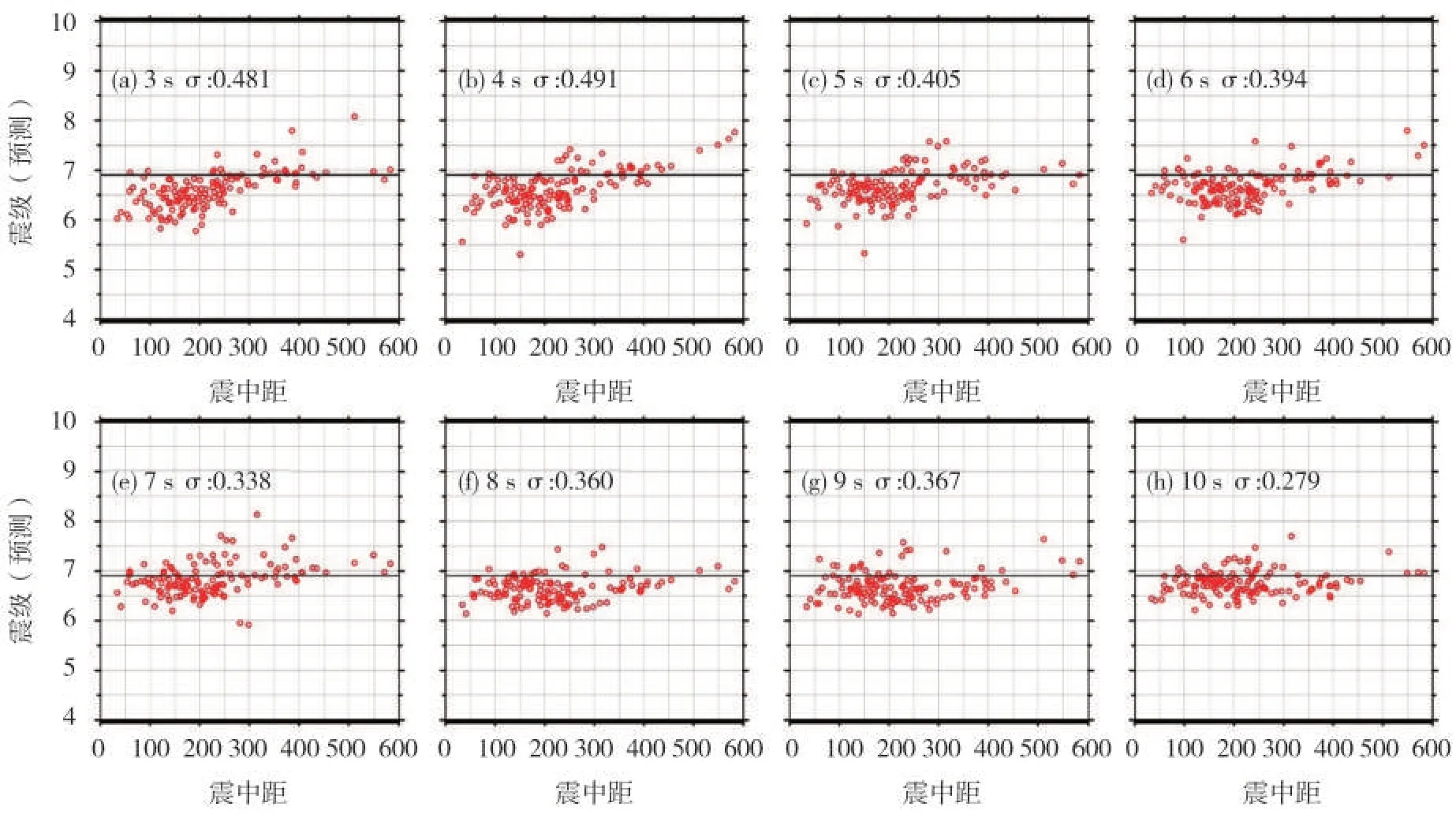
图13 P波触发后3～10s时间窗宫城地震估算结果Fig.13 Magnitude estimation results of Miyagi earthquake in the time window of 3～10 s after the P wave arrivals

针对前几秒时间窗时模型估算结果存在的震级低估和离散性较大现象，分析认为：本文在训练CNN-M模型时使用的KiK-net 台网数据最大震源深度为50 km，而宫城Mj6.9 级地震的震源深度为59 km，震源深度超出范围，使得模型对其前几秒波形的幅值信息、频率信息、能量信息的利用难度加大。

针对宫城地震，我们挑选出震中附近最先触发的22 个近场台场数据，不考虑各台站监测到P 波到达先后顺序，22个台站使用固定时间窗的震级估算模型，如3 s时所有台站统一使用3 s时间窗震级估算模型，对其估算结果进行分析。图14展示了22个台站在3～10 s各时间窗内的震级预估结果的均值和标准差，图中黑色条柱反应的是随时间窗变化的标准差，图中显示的各时间窗震级估算均值采用各台站震中距加权计算，距离越近的台站其记录数据质量越高，且可以为后续预警信息发布争取更多的时间，故权重越大，按此原则定义均值估算均值MWR计算公式如下

式中：Mi为第i个触发台站的估算震级；Ri为被触发的第i个台站的震中距；n为所选用的台站数目。

从图14中可以发现：选取的22个近场台站记录，在各时间窗内都保持了较高的震级估算准确性，3～6 s时间窗内估算结果逐渐靠近真实值，有部分台站已经成功估算出真实震级；后续7～10 s时间窗内估算结果均值略有降低，估算结果均值始终维持在Mj6.7级，误差0.2震级单位，较为靠近真实震级。

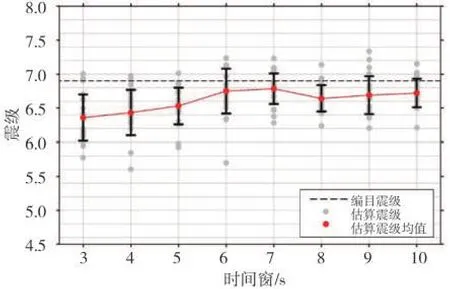
图14 3～10 s各时间窗内近场22个台站震级预估结果Fig.14 Magnitude estimation results of 22 stations in the near field in the time window of 3～10 s

此外，按照P波传播依次触发台站的时间顺序，以首个台站检测到P波到时为时间原点，以1 s为时间间隔，挑选出了10 s内依次触发台站的数据进行实时震级估算分析。台站记录到的该次地震数据时间窗越长，其包含的地震动信息越多，其计算出的震级也更具有可靠性，因此其权重越大，按此原则定义首台监测到P波到后各时间窗内的全部台站加权平均震级MWT计算公式为：

式中：Mi为第i个触发台站的估算震级；Ti为被触发的第i个台站用于估算震级的时间窗；n为所选用的台站数目。

图15展示了地震发生后的震级估算结果随时间的变化，使用当前时刻下各台站检测到的全部波形数据输入到对应时间窗的震级估算模型中以求得其估算震级，使用各时间窗下所有触发台站的估算结果平均值作为该时间窗的地震震级估算结果。图中黑色条柱表示模型实时震级估算结果随时间窗变化的标准差，实心圆旁边的数字代表触发的台站数目。

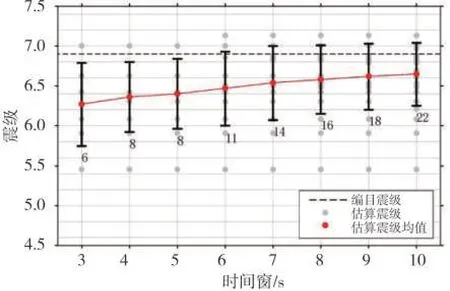
图15 CNN-M模型实时震级估算结果Fig.15 Real-time magnitude estimation results of CNN-M model

图15 中的震级随时间变化曲线，可以较为真实反应地震波触发首台后10 s 内台网震级估算实际情况。首台触发后3 s 时估算结果为6.27；4 s 时一共有8 个台站参与震级估算，结果为6.36；5 s 时仍为8 个台站触发，震级估算结果增加至6.40。随着地震波的传播，越来越多的台站被触发，近台包括的信息逐渐丰富，结果开始趋于稳定并接近真实值，10 s时共有22个台站，估算结果达到6.65。考虑到前文研究中提及的震源深度较深问题导致模型难以快速估算出宫城地震的实际震级，因此CNN-M 模型的最终估算结果稳定为6.6 级。从图15 可以发现：在首台触发后8 s，模型估算结果已经稳定在6.6 级，离散性较小，此时CNN-M 模型的多台估算结果已经趋于稳定，说明本模型具有可靠稳定的快速震级估算能力。

以上两次震例的分析研究结果表明：本文构建的CNN-M 模型在3 s 时间窗时部分台站即可准确估算出实际震级，表明此模型在一定程度上克服了传统模型存在的6.5 级震级饱和现象。随着时间窗长的增加，CNN-M 模型成功估算震级的结果逐渐增多，各台站估算结果均值也逐渐趋于稳定，在长野地震震例测试中，6 s 时间窗时各台站的震级估算结果逼近实测震级，表现较好。在宫城地震中CNN-M 模型在对震级进行估算时表现出了优秀的稳定性与可靠性，首台触发10 s时震级估算误差稳定在0.30震级单位内，结果仍旧存在一定的震级低估问题，说明本文的方法仍需进一步改进。

5 结论及讨论

本文以更准确持续估算地震预警震级为目标，利用P波触发后3～10 s内的日本KiK-net强震台网数据，基于人工智能机器学习领域的CNN 卷积神经网络方法，选用台站记录的11 种P 波特征参数、强震记录方向和震中距参数输入，构建CNN-M模型，并与传统“Pd方法”进行对比。获得的认识如下：

（1）通过使用日本KiK-net强震台网地震数据确定训练数据集构建CNN-M 模型，并基于测试集数据进行震级估算，结果表明：3～10 s 时间窗训练集误差为0.347～0.205，测试集误差为0.336～0.251，误差较为接近。经过测试和后续震例分析，表明CNN-M模型存在较为可靠的泛化能力。

（2）本文选用的数据震级范围为Mj3～Mj9 级，将CNN-M 模型得到的震级估算结果和传统的“Pd方法”对比发现，CNN-M 模型的结果误差和标准差都更小，说明其对地震预警震级估算有较高的可靠性，此外较之传统的“Pd方法”存在的大震震级低估问题，CNN-M模型对其有了较大改善。

（3）日本2014年长野Mj6.7级地震和2021年宫城Mj6.9级地震两次震例分析表明，构建的CNN-M 模型在P波触发3 s下即可在部分台站端成功估算出实测震级，改善了大震低估现象，且随着时间窗的增加，估算结果逐渐稳定可靠，在震级实施估算的研究中也取得了较好结果，验证了此模型在实际地震预警中的实用性。

该工作仍有不足之处，如尚未开展对各台站的场地效应研究，此外如何区分利用P波和S波到时后的不同信息来进行震级估算，这些方面都应当是后续的重点研究方向。