分块矩阵在矩阵秩理论教学中的探讨
唐大钊,李 丹
(1.重庆师范大学数学科学学院,重庆 401331;2.重庆市大学城第一中学,重庆 401331)
分块矩阵不仅是高等代数课程中的重要内容,而且也是相关后续课程中研究问题的重要工具。作为反映矩阵固有特性的重要指标——矩阵秩,它不仅是向量组秩横向和纵向的推广,而且是构成矩阵理论的基石。因而,矩阵秩之间的关系(等式关系、不等式关系)的证明及推导就显得非常重要。然而,有关矩阵秩的等式和不等式不胜枚举,如何以一种较为有效的方式统一地去处理这类问题是每一个高等代数授课老师需要思考的问题。
矩阵的分块是处理矩阵一种有效方法,它能使阶数较高矩阵的计算变得简洁和快速,容易被学生接受和理解。此外,矩阵的分块这一处理方式能进一步开拓学生思维,对于提高学生灵活解决问题的能力,进而培养学生的创新思维能力都有积极作用。基于笔者近年来对于高等代数和线性代数课程的教学经验,本文将主要探讨分块在矩阵秩理论中的应用,包括利用矩阵的分块证明矩阵中的若干重要定理,以及涉及矩阵秩的若干不等式。从实际效果看,这些探讨增强了学生对于高等代数矩阵秩理论章节的理解,相当程度上改善了教学效果。
1 矩阵的秩、矩阵的分块及其相关运算
在本节中,我们主要回顾矩阵的秩和矩阵的分块。
定理1.1[1]矩阵的行秩(列秩)指矩阵的行(列)向量组的秩。因为矩阵的行秩等于列秩,因而将其统称为矩阵的秩,记为。
定义1.1[2]初等矩阵是将单位矩阵进行一次初等变换得到的矩阵。
定理1.2[4]矩阵的初等变换不改变其秩。
接下来,我们回顾在处理阶数较高的矩阵时一个重要的工具——分块矩阵。将某些给定的大矩阵看成若干小矩阵组成,就如同将矩阵看成由一个个数组成一样。在矩阵的相关运算中,将这些特定划分好的小矩阵当成数一样来处理,这一处理方式就是所谓矩阵的分块。唯恐言之无物,我们试举下面的例子来加以说明。矩阵
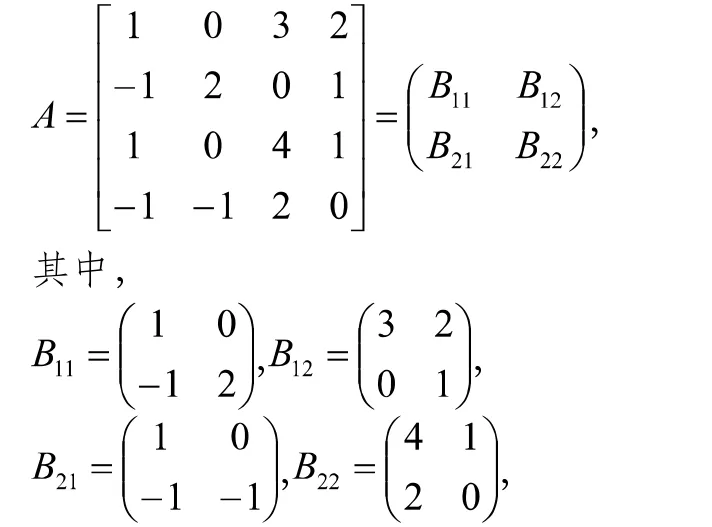
这就是我们所说的矩阵的分块。
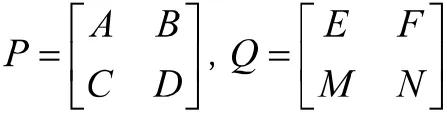

2 分块矩阵在矩阵秩相关定理中的应用
在本节中,我们将探讨利用分块矩阵对矩阵秩相关定理的证明。



3 分块矩阵在矩阵秩不等式关系的应用
分块矩阵不但为讨论抽象矩阵和抽象矩阵的秩构造了一架桥梁,而且分块矩阵与矩阵的初等变换是紧密联系的,利用矩阵的分块,可以对一些抽象矩阵的秩进行更深一步的讨论。在本节中,我们给出三个例子,探讨分块矩阵在矩阵秩中的应用。


分析:虽然上述条件是以行列式的形式给出的,但是题设中也不乏矩阵的秩之间的关系,而且行列式与其所对应的矩阵之间具有非常紧密的联系,这自然而然想到利用分块矩阵。



4 总结
一方面,分块矩阵对于行列式的计算和证明有着非常巧妙的应用,这主要体现在简化行列式的计算上。分块矩阵可以将一些高阶行列式通过分块以及其他的一些初等变换,简化为求一些较为低阶行列式的问题,由于行列式与其对应矩阵的秩之间有着非常密切的联系,因而分块矩阵是计算和证明行列式等式或不等式的一个有力的工具。
另一方面,在证明矩阵秩相关不等式的过程中,分块矩阵仍有不可忽视的作用,因为分块矩阵将具体的矩阵抽象为一些“小”矩阵块,这就在处理问题的时候提供了许多简捷的技巧;分块矩阵对处理矩阵的秩方面尤其便利,它将一些抽象矩阵,通过初等变换转化为一些基础矩阵(如单位矩阵、可逆矩阵等)的问题,这使得问题在一定程度上获得简化。不仅如此,分块矩阵对于研究矩阵的性质(如逆矩阵、矩阵的特征值、Jordan标准型等)也有着非常重要的应用。
综上所述,分块矩阵在处理涉及矩阵秩的相关不等式时,体现出了强大的统一处理能力。然而,学生需要就具体问题熟练地挑选或者构造出相关的初等矩阵,这就需要平时多对相关习题中分块矩阵的选取进行观察、归纳和总结。另一方面,教师在讲授完分块矩阵这一工具后,也应该帮助或者引导学生对其进行系统归纳和总结。总之,笔者认为,为了使学生更好理解高等代数这门课程,教师应当根据教学大纲和授课对象,选取最优的教学内容和合理的教学方案。在教学过程中,可以及时对所学知识进行系统归纳并进行相关应用,使学生真正体会到高等代数这门课程的真正魅力所在,提高其学习积极性,实现最佳的教学效果。

