“双碳”约束与经济增长

孙中才

（中国人民大学农业与农村发展学院 北京 邮编：100872）

一、引言

现代经济学的第一个定律——自由市场自行调节，证明了市场的自然存在性，其运动是自然的一种调节过程[1]。现代经济学前沿范式——G函数的确立，使得表示这种自然存在及其调节过程的形式更加明确且更加便利。20世纪中后期，随着环境污染、人类生活质量下降，环境容量（Environmental Capacity）日益成为经济增长的约束条件之一[2]。其中，有两个指标已经作为具体的量化数值，进入经济增长过程，这就是碳达峰（Peak carbon dioxide emissions）和碳中和（Carbon Neutrality）[3]。能够看出，这两个指标对于碳排放（Carbon Emission）的作用而言，是不同方向的，因而对经济的影响应该是不尽相同的。这给以F函数为范式的经济分析带来了不小的困难，但对于前沿范式G函数来说，便很容易解决[4]。这主要是因为，G函数可以在经济体概念的基础上，很直观地把碳达峰和碳中和的量化数值归入约束条件之列，并作为广义需求向量的特定元素体现在经济体的结构之中，从而依据数学语法逻辑得以分析，令有关规律得到揭示和解释[5]。在静态分析里，一般而言，若最优化模型其余条件不变、只是增加了有限的几个约束条件，那么继续完成求解，应该并不困难。但这通常意味着是局部的点集逼近性分析，距离经济的实际运行过程较远，准确性和精确性欠缺。为此，已经出现了一些动态分析的尝试，把有关峰值约束直接嵌入经济增长运行过程里，再通过增长状态分析，解释这种约束对经济增长的影响作用[6]。这种直接外嵌入硬性约束的做法，简单易行，实际效果应该很明显，主要不足在于，就技术而言，它仍属于事后纠正的技术，还不是现事前给定的控制预想，难于实现经济预设[7]。

为尝试着弥补这样的不足，在这篇论文的以下部分里，将给出碳达峰和碳中和的“内生式”指标，并进而对它们的实际经济作用展开讨论。

二、经济的运行过程

动态的有约束的利润函数——G函数的一般结构为：

式中，π(.)——利润；a——科技进步矩阵，；p——产出价格向量，p= [p1p2…pi]；pi＞0，i=1,2, …,I；v——需求数量向量v= [v1v2…vJ]，vj≤0 ，j=1,2, …,J， 有I≤J；t——时间。

依据数学对偶理论和生产可能性凸集定律，我们知道，式（1.1）的初始状态是一个纳什均衡，也就是一个由各个局部最优化结果组成的经济体最优化结构[4,10]。在这个初始状态上，即在t= 0时刻，其内部存在着如下的固定替代弹性：

式中，S——固定替代弹性矩阵；σpi ph——第i种产出的价格对第h种产出的价格的替代弹性；σvjph——第j种需求数量对第h种产出的价格的替代弹性；σpivk——第i种产出的价格对第k种需求数量的替代弹性；σvjvk——第j种需求数量对第k种需求数量的替代弹性；

而且，由因子最小被替代法则（Law of Factors Minimum Substituted）所决定，在时刻t= 0，经济体内必定处于如下这样的初始状态：

i，h=1,2,...,I，h∈i,h≠i，j，k=1,2,...,J，k∈j,k≠j，并有I≤J。

式中，Δrpi(0)——第i种产品价格的被替代率，i=1,2,...,I；σpi ph——第i种产品价格与第h种产品价格之间的固定替代弹性值；rahh——第h种产品的科技进步增长率；rph——第h种产品的价格增长率，——第i种产品价格与需求数量Vk之间的固定替代弹性值，——需求数量vj的被替代率，j=1,2,...,J；σvj ph——需求数量vj与第h种产品价格之间的固定替代弹性值σvjvk——需求数量Vj与需求数量Vk之间的固定替代弹性值——需求数量vk的增长率，k=1,2,....,J。

选取2017年6月～2018年6月院内收治的患有心血管疾病的患者86例作为研究对象，将其随机分为对照组与观察组。其中，男54例，女32例，年龄55～86岁，平均（68.25±2.84）岁；高血压28例，高脂血症19例，心律失常22例，心肌梗塞17例。两组患者一般资料对比，差异无统计学意义（P＞0.05）。

式（1.3）-（1.4）意味着，如果在t= 0时刻给定经济的初始条件π（ap,v,t） ，若这个经济体是正常的话，也就是可以正常运行的话，那么，市场价格pi和需求数量vj便必定自然地呈现出以固定替代弹性为坐标的被替代状态这一特性，就是经济的正则性[8]。

容易理解，经济的正则性是一种自然性质。外来的干预或干扰可以改变经济的运行状态，但不能改变这种正则性，因为任何干预或干扰，只可改变参数或变量的增长率，而不能改变固定替代弹性值，更不能改变市场自然调整的经济容量最小被替代法则(Law of Minimum Economic Capacity Substituted)，或称经济容量的最小受限制法则(Law of Minimum Economic Capacity Restricted)，也就是如式（1.3）-（1.4）所示出的内容。因而，在各种外来因素的作用下，经济的结构会有所变化，但其正则性不变，经济要沿着其内在不变坐标而正常运行的性质不变，除非这种结构遭到了过分的干预或干扰，以至于到了被破坏的程度，使得经济已经不能在经济容量所允许的正常轨道上运行了。从基本逻辑上来看，经济的正则性在每个因子被替代的意义上应该是很容易理解的。在市场上，每个经济当事人追求利润最大化而形成纳什均衡。而作为它的对偶形式，G函数必然表现为需求支出最小化，导致每个经济因子的被替代程度最小化，即广义的因子扩张才能保障利润扩张[9]。

从纳什均衡定理和数学对偶结构来看，在自由市场上，经济当事人在服从市场价格和约束条件，诸如需求或资源等前提下，追求各自的利润，从而展开竞争。这不仅给市场不断地注入动力，还在市场里形成了一个追求利润最大化的共同的目标。结果，导致经济体在自然的运行格局里，均呈现出因子被替代最小化的运动态势，见式（1.3）-（1.4）。

容易发现，在式（1.4）中，必定存在一个

也就是说，在各个需求数量的最小的被替代率中，必定存在着一个全局性最小的被替代率这个具有全局性最小被替代率的经济容量，便是短板需求[5,52]。

能够看出，在这个短板容量的表达式

中，只有rp（h0）是变量，其余都是常量。于是，可以解得：

即可以解得一个全局最小的价格增长率，也就是短板价格。为简单起见，可以把短板价格表示为：

这样，加上短板需求在内，在经济体里便得到了一个全局最小的向量，也就是短板向量：

于是，经济的运行，便向着这个短板向量所给定的参数和变量收敛。如果其余条件均未改变，运行时间（t＞0）又足够长的话，那么，其理想的收敛极限为：

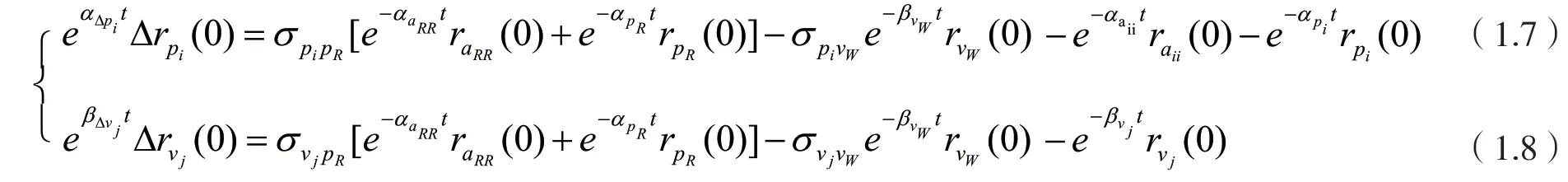
在这里，人们可以看到，得出式（1.5）和（1.6）的过程都是经济体的自然存在或自然行为。给定了初始条件以后，经济便会自然地遵循内在的规律进行自我收敛和调节。

容易理解，经济体由式（1.3）-（1.4）所示出的初始状态发展到式（1.7）-（1.8）所表示的状态，可以视为是一个运行周期。其所需要的时间长度，可能要视经济体的具体结构和条件而定。在这个时间长度，即时程里，经济体的结构会发生一些变化，也就是会呈现为增长进程中各个部分不同而接续替代的格局。格局组分成分的大小，和形成一个格局的时程的长短，体现着经济体增长的规模和速度，也就是效率。经济体的状态由式（1.3）-（1.4）变化到（1.7）-（1.8），应该涵盖着不少局部的、短暂的效率增高过程。式（1.7）-（1.8）是一个周期里效率提升至最高的结果。

三、碳达峰值与碳中和值的运动

为便于表示，不妨在式（1.1）里的需求数量向量 中的元素，定义 1v——碳达峰值；v2——碳中和值，

关于经济运行过程的分析结果表明，在正则规律指引下，经济体必定由初始状态式（1.3）-（1.4）变化到终点状态式（1.7）-（1.8）。也就是说，初始状态

必将在短板向量的作用下，做收敛性增长。如果其余条件均未改变，运行时间又足够长的话，那么，在终点上，其理想的收敛极限为：

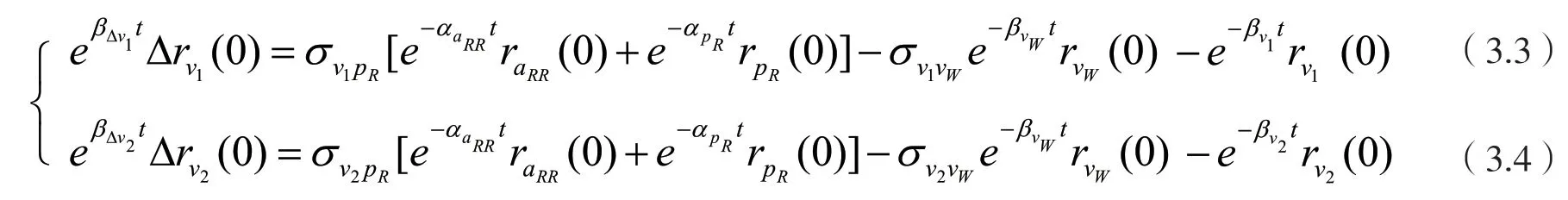
上述分析结果表明，式（3.3）-（3.4）是式（3.1）-（3.2）的极限状态，即在给定的这个运行期间内，碳达峰值v1和碳中和值v2的被替代率分别以为收敛的极限，也就是说，在这个运行周期里，各个时间点上的实际碳达峰值和碳中和值的被替代率都不及这两个被替代率。而在接续下来的新周期里，若没有新的介入因素导致它们变化，这两个被替代率，即将作为下一个周期的初始状态参数而存在。

由此，人们很容易想到，若在经济运行的初始状态式（3.1）-（3.2）里，便人为地给定了式（3.3）-（3.4），那么，在上述的经济运行终点状态里，碳达峰值和碳中和值必定始终以给定的这两个状态参数为极限而运动，那么，在整个运行过程中，经济会以内生性的约束状态，始终遵循着这两个约束而运动。从而，使得经济能以内在控制的状态满足碳达峰和碳中和的要求。一般地讲，这样的约束应该比静态的硬性规定更容易实现[10]。

从事后管理走向事前管理是现代经济发展的一大进步，对碳达峰和碳中和约束的事前设定，会越来越重要，也越来越必要[11]。事前给定碳达峰和碳中和约束的被替代率指数，需要通过短板向量来估计，而短板向量的两个元素——短板需求与短板价格，在给定初始状态便很容易求得，进一步根据短板元素被替代率的预测值，可以估计出碳达峰和碳中和被替代率的指数，从而完成上述的关于这两个约束的被替代率的估计。

或许有人对被替代率的概念不是很熟悉，但是对增长率的概念一定不陌生。被替代率与增长率的指数是绝对值相等、符号相反的数值[12]。据此，把被替代率转换成增长率，或许可以有助于理解和把握。

另外，在进行上述碳达峰和碳中和“内生式”约束值估计的过程中，因为这两个约束值的指数预测值，应该存在一定的差距，那么，人们能够很容易发现，现实的经济体结构是对碳达峰约束有利，还是对碳中和有利。这可能对有关决策不无益处。自然，对于不同的经济体之间，进行类似的比较，也是可以实现的，并且，也应该是很容易的。