洞悉统计本质 彰显分析素养——浙江省2020年中考“统计与概率”专题命题分析

马学三

一、 前言

统计与概率是初中数学教学的核心内容，也是今后培养学生数据分析素养的基石，更是中考命题的重要载体。综观2020年浙江省各地区的中考数学试卷，统计与概率继续以较高的比重存在，分析发现着重考查了随机事件及发生的概率，题型涉及选择题、填空题和解答题，且大部分为中、低档难度的题，全面覆盖统计与概率的基础知识、基本技能和基本方法。在解答题部分，更注重考查学生的数据分析观念与数据处理的意识，考查的知识点也更为全面和综合。总体上看，2020年浙江省各地区中考统计与概率试题在命制之初已考虑到分层、分梯度设置，给不同层次的学生都提供了展示的机会。

在数学教育向培养学生数学核心素养的趋势下，历年中考数学中统计与概率部分的命题趋势也有所变化，题目的设计更加贴近数学素养的内涵。2020年中考数学统计与概率继续关注对数学分析素养本质和内涵的考查，适度增加学生熟悉的情境，抽象出数据分析背后的内容，注重考查学生的理性思维和逻辑推理能力、数据分析能力，增强了实用性和创新型，通过设计情境渗透人文思想，彰显出数学中蕴含的素养内涵。

二、 命题形式与考查核心素养分析

(一)基于统计思想和抽样本质的考查，巩固“双基”，迁移应用

抽样是初中数学统计课程的一个主要内容，简单随机抽样在实际生活中应用较多，数据分析能力是学生需具备的数学核心素养之一。近几年来，中考试题中关于简单随机抽样的考查范围较为明确，考查形式越来越注重在实际生活中的应用意识。

【例1】(杭州卷)某工厂生产某种产品，3月份的产量为5000件，4月份的产量为10000件。用简单随机抽样的方法分别抽取这两个月生产的该产品若干件进行检测，并将检测结果分别绘制成如图1所示的扇形统计图和频数直方图(每组不含前一个边界值，含后一个边界值)。已知检测综合得分大于70分的产品为合格产品。

(1)求4月份生产的该产品抽样检测的合格率。

(2)在3月份和4月份生产的产品中，估计哪个月的不合格件数多？为什么？

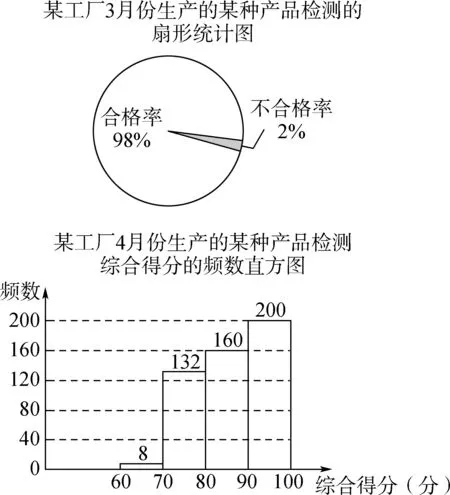
图1

【例2】(台州卷)新冠疫情期间，某校开展线上教学，有“录播”和“直播”两种教学方式供学生选择其中一种，为分析该校学生线上学习情况，在接受这两种教学方式的学生中各随机抽取40人调查学习参与度，数据整理结果如表1(数据分组包含左端值不包含右端值)：

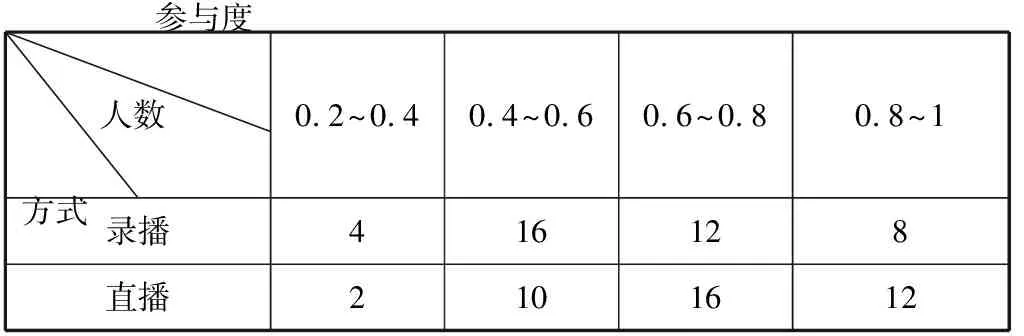
表1

(1)你认为哪种教学方式学生的参与度更高？简要说明理由。

(2)从教学方式为“直播”的学生中任意抽取一位学生，估计该学生的参与度在0.8及以上的概率是多少？

(3)该校共有800名学生，选择“录播”和“直播”的人数之比为1∶3，估计参与度在0.4以下的共有多少人？

【评析】以上两道题以实际问题为载体，考查了学生解决实际问题的能力，以及对数据的理解与分析的能力，很好地渗透了对抽样知识迁移能力的考查。例1注重检测学生收集与整理简单抽样数据的能力，考查了统计图表的转换，以及学生的推理能力。例2从客观实际背景出发，主要考查学生利用样本数据去估计总体情况的能力。数据分析核心素养明确提出注重对学生收集和整理数据能力的培养，以上题目的设计对学生数学核心素养的提高具有积极作用。

(二)统计图表的绘制与数据转化的综合考查，峰转“四基”，暗戳素养

描述数据的重要手段之一就是统计图表的表示，能够更直观地表示数据。从初中生数据分析核心素养发展水平情况来看，在读懂条形统计图、折线统计图、扇形统计图以及频数直方图的基础上，能够绘制简单的统计图表。2020年中考统计与概率试题继续考查统计图表的分析与绘制，通过考查统计图表的基本概念、本质意义，以及数据的计算，增强统计与概率知识考查的基础性，使学生透彻掌握统计的基础知识，有利于学生数据分析核心素养的达成。

【例3】(宁波卷)某学校开展了防疫知识的宣传教育活动。为了解这次活动的效果，学校从全校1500名学生中随机抽取部分学生进行知识测试(测试满分100分，得分x均为不小于60的整数)，并将测试成绩分为四个等级：基本合格(60≤x<70)，合格(70≤x<80)，良好(80≤x<90)，优秀(90≤x≤100)，制作了如下统计图(部分信息未给出)。

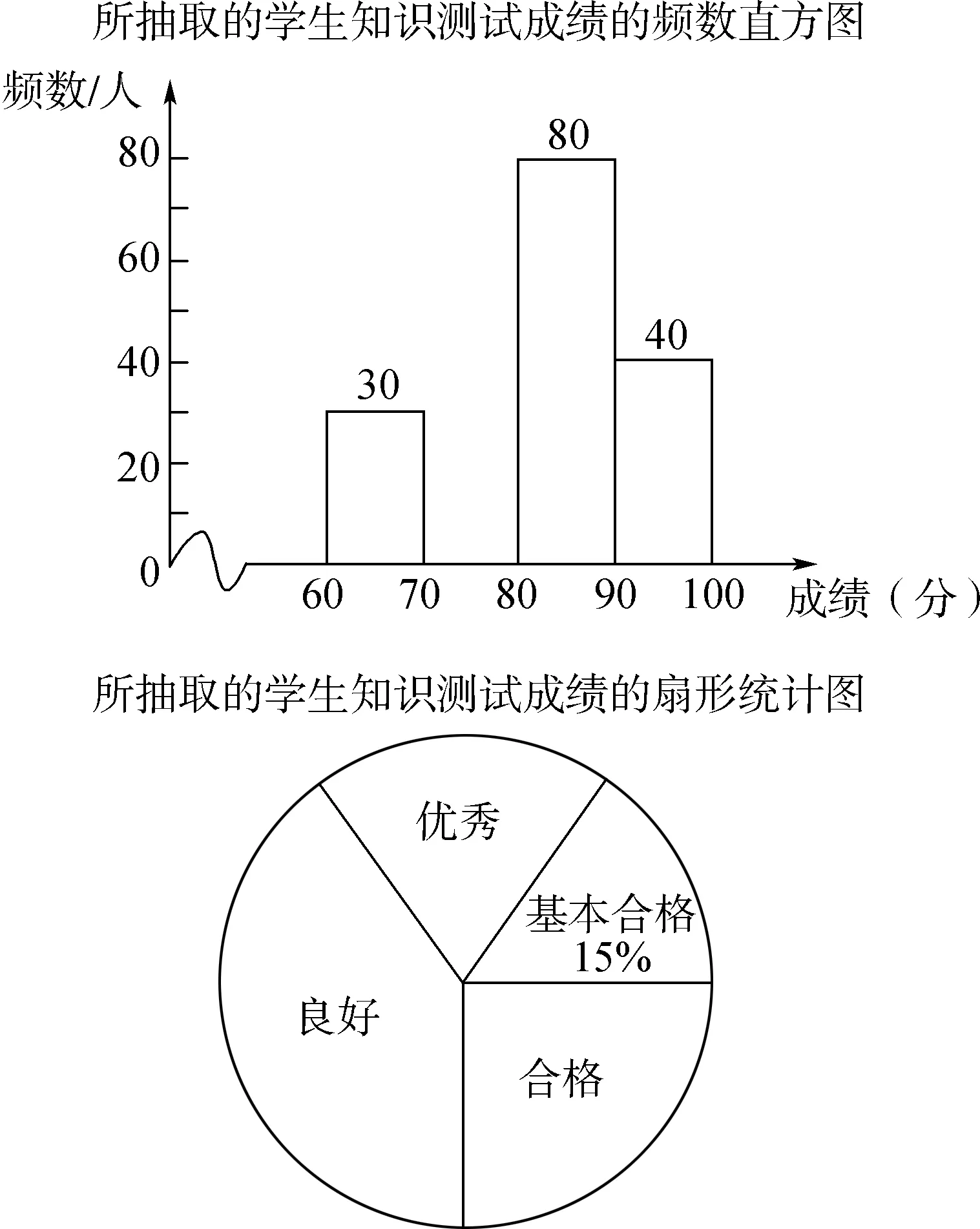
图2

由图中给出的信息解答下列问题：

(1)求测试成绩为“合格”的学生人数，并补全频数直方图。

(2)求扇形统计图中“良好”所对应的扇形圆心角的度数。

【例4】(衡州卷)某市在九年级“线上教学”结束后，为了解学生的视力情况，抽查了部分学生进行视力检测。根据检测结果，制成下面不完整的统计图表。

表2 被抽样的学生视力情况频数表

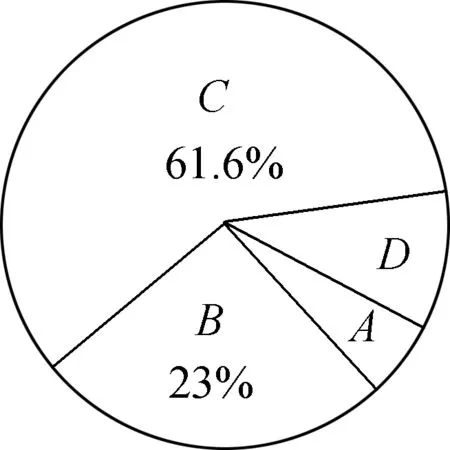
图3

(1)求组别C的频数m的值。

(2)求组别A的圆心角度数。

(3)如果视力值4.8及以上属于“视力良好”，请估计该市25000名九年级学生达到“视力良好”的人数。根据上述图表信息，你对视力保护有什么建议？

【评析】例3以学生熟悉的生活情境作为背景，令学生根据题目中的信息，进行统计图表的分析与完善，潜移默化中考查了学生对统计概率图表表示方法的理解与运用，着重考查了学生的作图能力与数据分析意识。尤其考查了学生对频数直方图与扇形统计图数据的转变，使统计概念的考查水到渠成。图表本身作为数据关系的一种表露形式，图表的绘制可以从数量和图形双方面考查学生的综合计算能力，表露出统计本质的考查。例4对频数分布表与扇形统计图之间数据的关系进行全面考查，突出了基础知识、基本技能、基本思想方法以及基本活动经验即“四基”的重要性。通过给出的频数与占比进行分析能够快速对总人数进行求解，能够彰显统计思维的缜密性和灵动性。另外，本题的最后一问涉及基于数据的预测和结论，学生可以根据各个视力段人数分布占比获得有效信息。让学生根据数据分析的结果提出相关建议，此题较明确地考查了学生数据分析核心素养能力，这表明我国中考试题已经开始尝试对学生数学核心素养的测试。

(三)集中趋势和离散程度的分析考查，引导推理与探究，维度多元

《义务教育课程标准(2011年版)》中明确指出刻画一组数据集中趋势的统计量一般用平均数、中位数和众数来表示。通过以上数据的计算结果能够对调查对象发展的趋势进行判断，以便于做出应对的决策。而平均数、中位数以及众数由于定义的不同，进而数据表示的意义也存在较大的区别。

【例5】(杭州卷)在某次演讲比赛中，五位评委给选手圆圆打分，得到互不相等的五个分数，若去掉一个最高分，平均分为x；去掉一个最低分，平均分为y；同时去掉一个最高分和一个最低分，平均分为z，则

( )

A.y>z>xB.x>z>y

C.y>x>zD.z>y>x

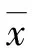
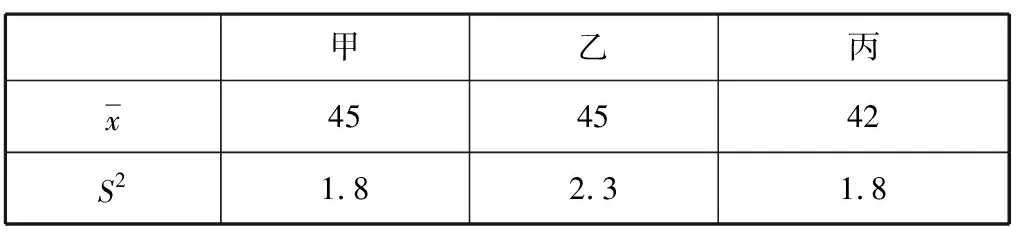
表3

明年准备从这三个品种中选出一种产量既高又稳定的枇杷树进行种植，则应选的品种是。

【例7】(温州卷)山茶花是温州市的市花，品种多样，“金心大红”是其中的一种。某兴趣小组对30株“金心大红”的花径进行测量、记录，统计如表4。

表4

这批“金心大红”花径的众数为

( )

A. 6.5cm B. 6.6cm C. 6.7cm D. 6.8cm

【评析】例5考查学生对平均分、最高分和最低分的区别与联系以及数据的计算能力，并对学生分析判断数据的能力进行了要求和考查。例6考查学生对平均数、方差概念的理解与运用，清楚两者的本质含义。本题需要学生从概念的角度辨别平均数和方差的内在区别，然后通过对数据的分析得出结果，凸显了数据对客观背景的真实反映，实际问题的解决更突出考验学生的数据分析核心素养。例7通过以本土文化作为数据产生的背景，描述出收集数据的细节，在一定程度上能够让学生在审题过程中感受到数据收集的过程与方法，以及主要考查了学生对众数概念的理解。

(四)随机事件及其发生概率的运算检测，贴近生活，夯实基础

2020年浙江省关于统计与概率试题，通过创设情境，立足于学生对实际问题的思考，考查学生数学逻辑推理能力，考查学生对数学题目的阅读理解能力，以此引发学生深入思考，让学生经历“抽象—分析—归一”的过程，考查学生对随机事件的理解和解决问题的能力。

【例8】(嘉兴卷)一只蚂蚁在如图4所示的树枝上寻觅食物，假定蚂蚁在岔路口随机选择一条路径，它获得食物的概率是。

图4

【例9】(宁波卷)一个不透明的袋子里装有4个红球和2个黄球，它们除颜色外其余都相同，从袋中任意摸出一个球是红球的概率为

( )

A. 1/4 B. 1/3 C. 1/2 D. 2/3

【例10】(杭州卷)一个仅装有球的不透明布袋里共有4个球(只有编号不同)，编号分别为1，2，3，5，从中任意摸出一个球，记下编号后放回，搅匀，再任意摸出一个球，则两次摸出的球的编号之和为偶数的概率是。

【评析】例8引导学生经历从设计的情境中抽象出数学问题的过程，类似的试题在2020年全国各地区的中考试卷中都较为常见，与学生的生活实际息息相关。例9则引导学生体会随机事件发生的概率问题，注重考查学生的基本知识和基本能力，突出考查学生对随机事件发生概率的理解运用能力。例10则考查学生对放回再摸取事件的理解能力，使学生运用所学知识与方法解决此类概率问题，注重对概率本质特征的探究与理解，学生需要借助树状图或者列表表述简单随机事件所有可能的结果，更关注实际问题中学生对概率意义的理解。

(五)数学核心素养能力的考查，挖掘数据，表述结论

《普通高中数学课程标准(2017年版)》中关于数据分析素养的介绍中指出数据分析是指针对研究对象获取数据，运用数学方法对数据进行整理、分析和推断，形成关于研究对象知识的素养。数据分析过程主要包括收集数据、整理数据、提取信息、构建模型、进行推断、获得结论。这表明，中考中对数学统计与概率的考查应该包括对题目中数据的简单整理与信息的推断与提取。

【例11】(温州卷)A，B两家酒店规模相当，去年下半年的月盈利折线统计图如图5所示。

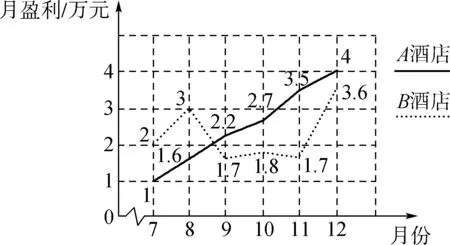
图5

(1)要评价这两家酒店7—12月的月盈利的平均水平，你选择什么统计量？求出这个统计量。

(2)已知A，B两家酒店7—12月的月盈利的方差分别为1.073(平方万元)、0.54(平方万元)，根据所给的方差和你在(1)中所求的统计量，结合折线统计图，你认为去年下半年哪家酒店经营状况较好？请简述理由。

【评析】随着对学生数学核心素养要求的提高，中考试题考查的内容越来越新颖，题目作答的类型也较为开放，例11主要考查学生解决实际问题的能力，问题(1)较为简单地考查了平均数的计算方法，问题(2)则更注重对学生数据分析思维的考查，让学生通过对方差以及折线统计图的分析，提取图中信息并分析作答。此题没有准确答案，只要阐述原因合理即可。此类题目是考查学生统计思维意识的重要载体，对改进并提高中考数学核心素养检测的有效性，提高学生数据分析素养能力具有积极作用。

三、 基本结论和命题趋势展望

通过以上对中考题型的分析可以看出，以数据分析为载体，对数据分析核心素养进行了多角度、多方面的考查。这样的试题设计不仅考虑到学生的分层发展，也透露出中考试题在逐步向核心素养检测方面靠拢。关注数学核心素养的落实，不仅考查对数学基本概念、定理、方法及数学思想的理解和运用，而且还关注数学文化及科学精神，强化学科育人，使考试成为落实“立德树人”的重要途径。因此，未来中考数学的命题趋势应是更加注重对学生数学思维能力以及生活情境的考查，对概率与统计知识模块，将会在接下来的中考中更注重学生对数据的感知意识与分析能力，开放性题目也会逐渐增多，即更注重对学生数据思维、数学素养的考查，具体体现在以下方面：

(一)从情境维度考查学生的数学核心素养

数学核心素养培养是当下基础教育数学课程与教学改革的热点，培养学生的质疑能力和创新精神建立科学合理的核心素养评价指标体系是当下迫切需要解决的问题。中考试题更注重从现实问题入手，设置学生熟悉的情境，主要考查学生对情境的理解与转化能力，有利于学生将所学知识迁移至实际问题中，增强学生的应用能力与应用意识，促使学生全面地认识数学与社会生活之间的关系，以此提高学生的创新能力与应用能力，进而达到提升学生数学核心素养的目的。

(二)从开放性结论维度考查学生的数学核心素养

中考正以开放性的问题设置考查学生对数据的感观意识，从实际生活中收集到的数据往往具有多重含义，让学生挖掘数据背后的意义有利于学生数据分析核心素养的达成，另外，从国际数学核心素养PISA测试的题目来看，题目的设计也较为宽泛，更多地与实际生活息息相关，为此，我国中考试题的设计可以参考国际测评标准，以达到更好地检测学生数学核心素养的效果。

(三)从知识迁移维度考查学生的数学核心素养

数学教学的目的是学生数学思维能力的达成，学生能够将所学知识迁移至其他问题的解决中，通过数学方法解决未知题目，更注重学生数学学习方法的应用、理解与创新，中考试题倾向考查学生对数学方法的掌握，数学思维的转化，数学知识的应用，解决问题的能力是考查学生数学核心素养的有效手段。