铁路编组站阶段计划动态调整方法研究
张 岩
(中国铁道科学研究院集团有限公司 运输及经济研究所,北京 100081)
阶段计划是铁路编组站作业指挥的核心环节,其编制质量直接关系到车辆在编组站的停留时间[1-2],进而对列车运行时间和铁路总体运输能力产生影响[3-4]。铁路编组站实际作业过程中存在着多种不确定性[5],已有学者以提高阶段计划的鲁棒性为目标,研究不确定条件下编组站阶段计划的自动生成方法,使阶段计划在不确定性事件的随机扰动下仍然保持最优[6-7]。然而,列车晚点等异常突发事件使得阶段计划无法保持最优性和持续可实施性,需要人工变更阶段计划后才能继续执行。铁路编组站阶段计划调整研究方面,宋宇[8]从硬件结构、软件结构、系统功能、系统流程4 个方面对编组站运输调度自动化系统进行设计;牛惠民[9]给出了到发列车作业地点动态调整方法;张明[10]设计了一种协调优化编组站调机运用和配流问题的模型;马亮等[11]将计划间冲突作为计划变更的触发条件之一,设计了计划间冲突的检测算法。在此,以作业数据实时反馈为基础,面向编组站整体阶段计划动态最优的目标,研究提出编组站阶段计划动态调整方法。
1 铁路编组站阶段计划动态调整方法
1.1 阶段计划动态调整流程
铁路编组站阶段计划动态调整总体流程如图1所示。编组站内信息系统约每1 h 可以接收铁路局集团公司调度所更新的列车预计到达时间,基于历史数据学习可预测专用线、货场、车辆段取回待分解车列的到达时间,到达列车取下本务机后为到达车列,将到达车列和取回车列统称为广义到达车列。根据对历史数据的机器学习,结合实时作业信息预测到达技术作业、解体、编组和出发技术作业过程的所用时间,利用人工智能算法结合列车和车辆相关信息进行车流动态推算,获得最优的解体、编组顺序和出发列车车流来源,为阶段计划调整提供依据。实时监测站内阶段计划的实施情况,基于作业过程用时预测和动态车流推算获得的解编顺序,动态计算各项作业的预计完成时间,每当铁路局集团公司调度所给出的列车预计到达时间和本站预测的取回车列、技术作业、本务机作业和调机作业等预计完成时间变化时,需要调用1 次动态车流推算模块计算1 次,获得当前最优的配流方案,车站调度人员根据现场车辆、股道、调机和作业人员的实时作业信息,决策并实施阶段计划调整。阶段计划采用循环滚动式调整规则,对时域数据进行连续不断的循环反复优化,以此来达到整个时间段内目标的最优化。

图1 铁路编组站阶段计划动态调整总体流程Fig.1 Overall dynamic adjustment process of phase plan for railway marshalling station
1.2 作业过程用时预测方法
1.2.1 数据预处理
为了确保动态车流推算结果的准确性,需要对到达技术作业、解体、编组和出发技术作业的作业过程用时进行精准预测。班组人员充足的编组站技术作业基本可以在30 min 以内完成,但是具体作业过程用时无法实时掌握,需要通过历史数据学习与实时数据采集,预测到达、出发作业过程用时。对排风摘管、列检、货检、试风等各项到达、出发技术作业过程用时单独进行预测,总的到达、出发作业过程用时为各专业技术作业过程用时的最大值。解体作业的基本作业过程分为调机至到达场、连挂车列、推送车列至驼峰信号机、溜放分解。编组作业的基本过程分为调机至峰尾、平面调车连挂各车组、牵出车列至出发场。应对每一个过程的作业过程用时进行预测,叠加出最后总的解体、编组作业过程用时。
各项作业过程用时可利用机器学习方法进行预测,预测模型建立前需要对数据进行清洗,将各维属性的数据类型处理为连续值或0-1 离散值。数据属性预处理结果如表1 所示。对一个有d个可能取值的离散属性,当d>2 时离散值的差值没有实际意义,需转为d个取值为0 或1 的二值属性。

表1 数据属性预处理结果Tab.1 Preprocessing results of data attribute
1.2.2 数据降维

数据降维主要是通过保存相关性REL较大的属性特征,降低数据属性的维度。针对到达、出发技术作业,分别计算排风摘管、列检、货检、试风等基本作业过程的实际用时与各数据属性之间的相关性。针对解体作业,分别计算调机至到达场、连挂车列、推送车列至驼峰信号机、溜放分解等基本作业过程的实际用时与各数据属性之间的相关性。针对编组作业,分别计算调机至峰尾、平面调车连挂各车组、牵出车列至出发场等基本过程的实际用时与各数据属性之间的相关性。最后保留相关性系数较大的数据属性,用于作业过程用时的预测模型训练,从而实现数据降维。
1.2.3 预测模型训练
针对编组站的各项基本作业过程进行数据属性降维后,需要分别训练各项基本作业过程用时的预测模型。首先进行训练集和测试集的划分,将80%的数据划分到训练集,用作基于机器学习的预测模型训练,将20%的数据划分到测试集。通过比较测试集合内真实作业过程用时与预测作业过程用时的方差,来验证预测模型的效果。对于效果较差的模型,需要继续采集增加训练数据来完善模型参数。
模型训练之前需要进行数据归一化,将数据取值范围线性变换为[0,1]。具体归一化方法如公式⑵ 所示。

作业过程用时预测神经网络模型如图2 所示。排风摘管、列检、溜放分解等作业过程用时预测的神经网络模型包括输入层、隐层和输出层[13],隐层又可包括多层,选择隐层数为1 的神经网络。设有m个输入属性,则输入层节点数为m,隐层有n个节点,输出为1 个作业过程用时的预测值。

图2 作业过程用时预测神经网络模型Fig.2 Neural network model for operation process time prediction
以包括m个元素的列向量X= [x1,x2,…,xm]T为特征向量样本,即为数据降维后包括列车长度、车辆数、禁溜车数量和空车数量等数据属性的输入列向量。n行m列的矩阵W为输入层到隐层的权重系数矩阵,n个元素的列向量B= [b1,b2,…,bn]T为输入层到隐层的偏置向量,包含n个元素的行向量P= [p1,p2,…,pn]为隐层到输出层的权重系数向量,数值c为隐层到输出层的偏置值,f为ReLU,sigmoid,tansig,purelin 等激活函数。各单项作业过程用时预测输出结果y的计算值如公式⑶ 所示。
[4][18] 费昭珣:《东南亚国家的城市化进程及其特征》,《东南亚研究》1999年第4期,第49-54页。

激活函数选用ReLU 函数,优化器选用Adam算法[14],面向不同的作业过程用时分别对模型进行多轮训练,并通过对隐层节点数量的调整后可获得有效的模型。
1.3 动态车流推算模型及求解算法
1.3.1 动态车流推算过程描述
基于作业过程用时的精准预测可获得精确的动态车流推算模型,设广义到达车列集合A= {a1,a2,…,ak}代表阶段内到达的车列和取回车列集合[6],按到达顺序排列为a1,a2,…,ak,tai代表第i个到达车列ai的到达时刻,k代表阶段内到达车列总数,T i到 和T i解 分别代表ai的到达作业过程总体用时和解体作业过程总体用时;出发列车集合D= {d1,d2,…,dl}代表阶段内出发的列车集合,按出发顺序排列为d1,d2,…,dl,tdj为本阶段内第j列出发列车dj的出发时刻,l代表阶段内出发列车总数,T j编 和T j发 分别代表dj的编组作业过程总体用时和出发作业过程总体用时。
1.3.2 动态车流推算模型约束条件


1.3.3 动态车流推算模型目标函数
首先应明确编组站动态车流推算模型求解的最优化目标,可以为阶段计划兑现率最高或车辆在编组站的停留时间最短等。阶段计划兑现率高体现在所有列车都可以按时发车,在站停留时间短可以转化为阶段时间内向区间发出列车包含的车辆最多[4]。设vij代表ai向dj配入的车数,则模型的目标函数可用公式 ⒁ 表示,以阶段时间内向区间发出的车数最多作为优化目标。

1.3.4 动态车流推算模型求解算法
蚁群算法是解决旅行商问题的一种有效的人工智能算法,可以在规定时间内寻找到NP 问题的满意解[15-16]。传统旅行商问题可描述为旅行商从一个城市出发经过所有城市一次,如何选择路径使总行程最短,实质是在一个带权无向图中找一个权值最小的哈密尔顿回路[17-18]。可以将铁路编组站动态车流推算模型求解问题抽象成带权有向图的最小权重路径求解问题,将到达车列集合A= {a1,a2,…,ak}视为k个城市,蚂蚁从当前时刻可行的任意到达车列出发,随机选择下一个时刻可行的城市,即到达车列,直至所有到达车列被选择完毕,目标是向区间发出的车数最多,即NUM最大。
编组站动态车流推算模型求解算法流程如图3所示。算法开始后需要初始化信息素矩阵,为每个到达车列之间弧上的信息素赋初始值,然后进行循环迭代,迭代次数超过预定值或获得收敛解时达到迭代停止条件,迭代结束,输出包括解体顺序的收敛解。进入一个迭代过程后需要将全部蚂蚁随机放到当前时刻可行的到达车列对应的城市上,循环逐个为每个蚂蚁根据随机迁移规则寻找一个路径,找出一个NUM值最大的最优路径后为所有城市间的路径更新信息素,循环进行下一次迭代。

图3 编组站动态车流推算模型求解算法流程Fig.3 Solution algorithm process for calculation model of dynamic vehicle flow distribution in marshalling station
模型求解算法流程中蚂蚁应用迁移规则随机选择下一个车列所用的随机迁移规则如公式 ⒂所示。

模型求解算法中的倒数第2 步,更新所有路径上的信息素时所用的信息素更新规则如公式 ⒃所示。

2 应用效果分析
2.1 数据降维效果分析
以利用高精度北斗定位人员作业手持终端、车号识别等技术对某编组站SAM 系统作业项目、作业股道、调机号、车次、车辆总数、开始时间、结束时间等数据进行补强获得的数据为例,利用公式 ⑴ 给出的残差相关系数计算公式计算数据属性与预测作业过程用时之间的相关性,进行数据属性降维分析,可以得到各项作业过程用时的主要影响因素。将解体作业中的溜放分解作业过程用时与数据属性之间的残差相关系数由大到小排列,根据公式 ⑴,溜放分解用时与各数据属性间的残差相关系数REL如图4 所示。从图4 可以看出,列车长度、车辆数、禁溜车数量、空车数量、解体钩数与溜放分解作业过程用时存在较大的相关性。通过相关性计算还可得出编组作业中的平面调车连挂各车组的作业过程用时的主要影响因素包括车辆占用的股道数量、停放位置、车辆数量、车辆长度等。到达技术作业中的排风摘管作业过程用时的主要影响因素包括作业班组、作业时刻、停放股道、列车长度、车辆数量、摘管数量等。出发技术作业中的货检作业过程用时的主要影响因素有作业班组、作业时刻、停放股道、列车长度、车辆数量等。
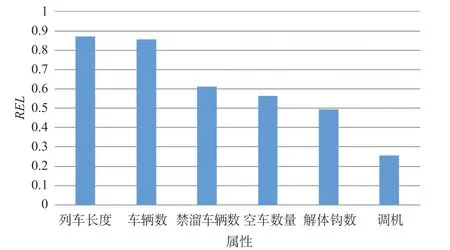
图4 溜放分解用时与各数据属性间的残差相关系数RELFig.4 Residual correlation coefficients between humping decoupling time and data attributes
2.2 作业时间预测效果分析
分别选取500 个到达、解体、编组和出发作业过程用时的样本数据作为测试集,单组数据的预测误差为预测值与真实值的绝对值除以真实值,测试集平均误差为单组数据误差的均值。选取样本数量不同的训练集分别进行训练,获得各作业过程用时预测模型,预测模型的隐层节点数量如表2所示。
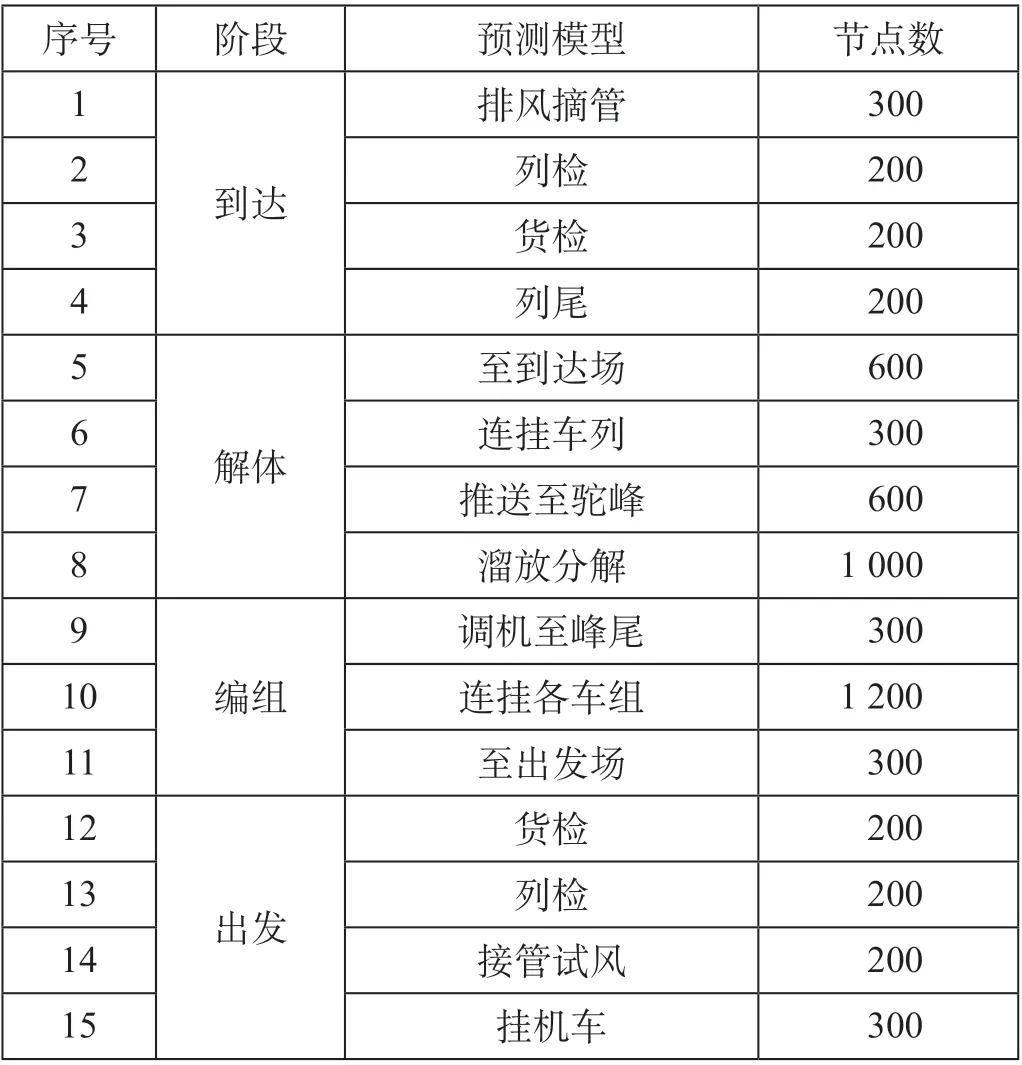
表2 预测模型的隐层节点数量 个Tab.2 Hidden layer node number of prediction model
不同样本数量下测试集平均误差变化趋势如图5 所示。随着样本数量的增加,各类作业过程用时的预测结果误差均逐渐减小,当样本数量达到10 000 时,到达、解体和出发作业过程用时的平均误差小于21%,编组作业过程用时的平均误差小于27%。

图5 测试集平均误差变化趋势Fig.5 Average error variation tendency of test set
2.3 动态车流推算算法求解效率分析
以3 级6 场布局的编组站为例,只针对上行出发列车计算阶段计划,设上行出发列车有15 组去向。上行出发场列车出发阶段计划根据阶段到达车列情况编制,可消化全部到达车列。上行到达场阶段内到达的广义到达车列数量为6 ~ 13 时,利用蚁群算法对动态车流推算模型进行计算求解,蚁群算法信息素的重要度α= 0.7,启发因子的重要度β= 0.7,信息素的蒸发系数ρ= 0.9。用i7 2.4GHz处理器和8G 内存配置的计算机进行求解,动态车流推算算法计算时间变化趋势如图6 所示。在确保阶段内全部列车满轴出发情况下,统计不同广义到达列车数量的收敛解计算时间。在阶段广义到达车列数量小于13 时,计算时间与到达车列数量之间存在线性的关系,算法可在3 s 以内获得最优解,满足阶段计划动态调整的实时性需要。

图6 动态车流推算算法计算时间变化趋势Fig.6 Calculation time variation tendency of dynamic vehicle flow distribution calculation algorithm
3 结束语
研究提出编组站阶段计划动态调整系列方法,利用提出的数据预处理和相关性分析方法,获得编组站到达、解体、编组和出发作业过程用时的主要影响因素,利用历史数据机器学习训练获得的神经网络模型可以较为精准地预测作业过程用时,提出的动态车流推算求解算法可以在编组站调度指挥实际业务要求的时间内获得最优的动态车流推算方案,对于实现我国编组站阶段计划编制和调整的智能化、提高编组站整体作业效率具有现实意义。

