突发事件对我国铁路客运量的干预特征研究

汪志红

（广东金融学院 金融数据与统计学院，广东 广州 510521)

0 引言

近年来，SARS、新冠肺炎疫情和各种自然灾害等突发事件对人们生活和社会经济造成不同程度的冲击，阶段性地影响着人们日常生活和社会发展。铁路作为我国重要交通工具，其客运量变化能够较为直观地体现某些突发事件对人民生活的影响，研究分析其冲击程度和发展趋势有利于更好地预防和应对将来可能引起的影响，这也是各级应急管理机构重点关注的问题之一。

突发事件对铁路客运量的影响实际上是一个突发事件的干预问题，这种干预可以运用干预模型来进行定量分析。学者们通常从2 个方面基于时间序列构建突发事件干预模型并进行干预分析：一类是将某些影响因素和政策措施作为时间序列的干预因素[1-2]，分析其干预常规变量对社会经济影响程度的大小，对其干预趋势进行研究。该类方法将铁路客运量分解为ARIMA 模型拟合值与突发事件干预因素，一定程度上忽视了干预因素与ARIMA 模型内部可能存在的关系。另一类是用脉冲函数或阶梯函数将某一突发事件作为干预因素，研究突发事件或政策干预的程度大小，同时研究其干预趋势，其研究过程为在识别时间序列异常值和最优ARIMA 模型基础上，对异常值进行基于脉冲函数或阶梯函数的虚拟变量针对性设计，确定干预过程的传递函数，与最优ARIMA 模型结合，构建时间序列的干预模型，这是当前国外时间序列干预研究的主流方法[3-5]，如Habib[5]等以现代避孕措施的三阶段作为阶段干预因素，对加纳和坦桑尼亚的公共卫生事件进行试验研究，得出带控制组的时间序列干预模型能够较为全面地分析公共卫生事件干预的变化过程。在该类方法的实际应用中，学者们更多地将干预因素作为时间序列干预模型整体的一部分进行研究，相对第一类方法更能体现模型设计的系统性，但对干预因素类型选择缺乏理论依据，同时缺乏对趋势干预过程的比较分析。时间序列模型在铁路客运量实际应用研究方面，X-13ARIMASEATS 或ARIMA 等时间序列模型更多地应用于铁路客运量的预测过程[6-9]，如钱名军等[6]运用SARIMA-GARCH 融合模型、SARIMA、ARIMA和NAR 动态神经网络模型对铁路月度客运量进行预测比较研究，认为SARIMA-GARCH 融合模型进行铁路客运量预测精度更高，但基于时间序列干预模型对铁路客运量的突发事件干预分析略显不足，可以在干预分析的基础上进一步细化铁路客运量预测过程，提高预测精度。

在此，针对突发事件对铁路客运量干预分析过程的不完善问题，应用X-13ARIMA-SEATS 季节调整方法中的自动检测突发事件离群值(异常值)功能，将离群值与脉冲函数或阶梯函数进行特征比较分析，科学确定突发事件虚拟变量类型，运用设计的虚拟变量在确定突发事件影响程度大小的同时，基于ARMA 干预传递函数分析突发事件对铁路客运量的冲击趋势，在总体上提升时间序列干预分析的科学性和系统性的同时，拓展时间序列干预分析在工程上的应用。

1 基于离群值冲击的干预传递函数设计

在X-13ARIMA-SEATS 季节调整中，通常将离群值分为4 种类型，第1 类为突发可加(Additive Outlier，AO)离群值点，是在某一时刻T受到异常突发事件冲击；第2 类为水平漂移(Level Shift，LS)离群值点，是从某时刻T瞬间变化到一个新的水平，并一直保持这一水平；第3 类为暂时变化(Temporary Change，TC)离群值点，为干预经过指数衰减回到原来水平；第4 类为斜线上升(Ramp Effect，RP)离群值点，为从T1时刻开始以线性速度逐渐变化到新的水平T2[10]。各离群值点表示形式如下。

式中：AOt为t时刻的突发可加离群值；t为突发事件干预发生的时间变量；T为突发事件干预时间点；LSt为t时刻的水平漂移离群值；TCt为t时刻的暂时变化离群值；α为经指数衰减回到原始水平的速率；RPt为t时刻的斜线上升离群值；T1为线性速率逐渐变化起点；T2为线性速率逐渐变化终点。

在时间序列干预模型中，将干预函数分为2 种类型，一种是在T时刻短期影响的暂时的脉冲函数，一种是从T时刻长期影响的持续的阶梯函数，干预函数各类型公式如下。

根据离群值和干预函数表示形式，并结合两者表现形式特点，使用干预函数构建离群值干预变量，此时，Pt(T)和St(T)被称为虚拟变量。根据干预过程影响时间的持续性特征，使用ARMA 模型表示干预传递函数。

假设干预为AO 离群值类型的暂时性干预，即只在T时刻(或滞后q阶)影响时间序列均值函数，则干预大小表示为

式中：Xt为干预大小；w为干预函数系数；B为滞后算子；q为算子滞后阶数。

以公式 ⑼ 为干预一般表示形式，结合离群值特点，4类离群值干预变化过程的传递函数表示如下[1-2]。

（1）AO 离群值导致干预发生，干预传递函数显示在T时刻(或干预滞后q阶)产生w的干预冲击。AO 离群值干预传递函数XtAO表示为

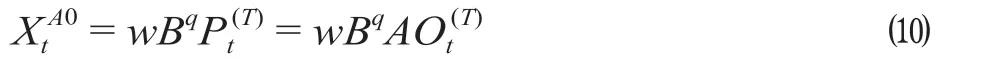
（2）LS 离群值导致的干预突然发生，使时间序列均值发生永久性变化，其干预传递函数表示在T时刻(或干预滞后q阶)处突然产生w的永久性干预。LS 离群值干预传递函数XtLS表示为

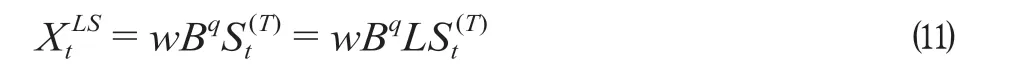
（3）TC 离群值导致干预开始，使时间序列均值产生短暂影响，干预传递函数显示在T时刻(或干预滞后q阶)处从干预w以指数级δ p逐渐回归到原来水平。TC 离群值干预传递函数XtTC表示为

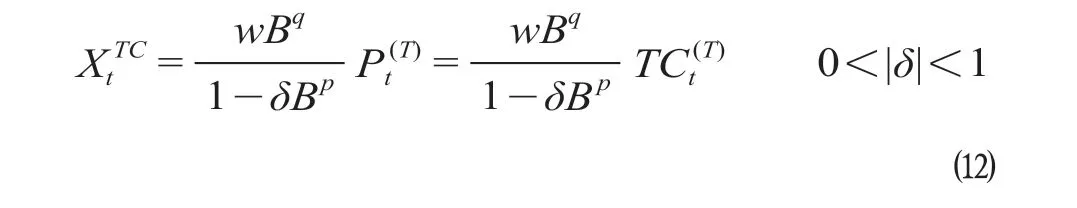
式中：δ为自回归多项式系数。

（4）RP 离群值导致干预发生，并产生永久性新水平变化，其干预传递函数显示在冲击的滞后q阶处从w1+w2以指数级δ p逐渐变化到新水平w2水平。RP 离群值干预传递函数XtRP表示为式中：w1与w2分别为滑动平均多项式系数。

将以上各类干预传递函数作为季节调整识别的最优ARIMA 模型的外生传递函数变量，即可得到如下时间序列干预模型。

式中：∇d为d阶非季节差分；∇SD为季节周期为S(此处周期为12)的D阶差分；Yt为铁路客运量时间序列；θ1，θ2，…，θq为残差非季节移动平均系数；ϑ1，ϑ2，…，ϑQ为残差季节移动平均系数；QS为季节移动平均滞后阶数；φ1，φ2，…，φp为残差非季节自回归系数；φ1，φ2，…，φP为残差季节自回归系数；PS为季节自回归滞后阶数；εt为零均值白噪音序列。

公式 ⒁ 中，前一部分为干预传递函数；后一部分为ARMA 模型部分，分子为q阶移动平均(MA)和QS阶移动平均季节多项式乘积，分母为p阶自回归(AR)和PS阶自回归季节多项式乘积。

2 铁路客运量干预模型构建

2.1 数据来源与特征分析

研究分析2002 年1 月—2020 年8 月铁路客运量数据，铁路客运量时间序列分布曲线如图1 所示。根据图1，铁路客运量表现出较强的季节性特征，且在2002 年与2020 年出现急剧下滑现象，说明有突发事件对铁路客运量造成重大激冷冲击。

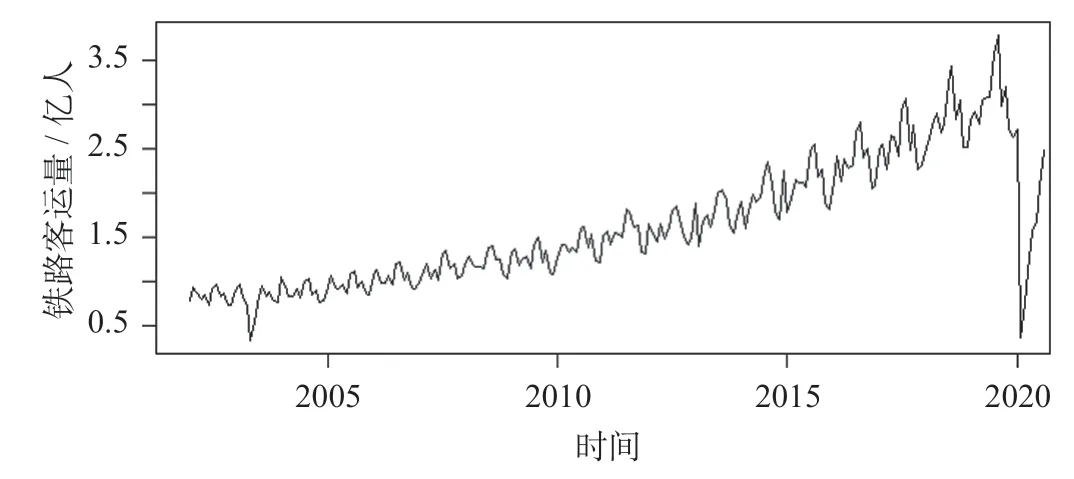
图1 铁路客运量时间序列分布曲线Fig.1 Time-series distribution curve of railway passenger volume

根据数据季节性特征显著、异常值凸显和月度数据特点，在考虑季节性、周期性、发展趋势和异常值影响等条件下，采用主要分析月度尺度和季度尺度时间序列的X-13ARIMA-SEATS 模型对其进行季节调整、最优ARIMA 模型识别和离群值检测。X-13ARIMA-SEATS 模型是X-12ARIMA 季节调整模型和TRAMO-SEATS 季节调整模型的结合，其优点一是增加X-12ARIMA 季节调整中Reg-ARIMA 模块的延展时间序列、自动识别ARIMA模型和检测离群值能力，增加移动假日(如中国春节等)和交易日效应及预测能力；二是使用SEATS程序和X-11 非参数调整方法，产生基于季节因素建模的ARIMA 预调整和预测方法[11-12]。

研究主要应用X-13ARIMA-SEATS 模型的最优ARIMA 模型自动识别、离群值检测和预测功能进行干预模型的设计与分析，得到季节调整结果。铁路客运量的X-13ARIMA-SEATS 季节调整结果如表1 所示。

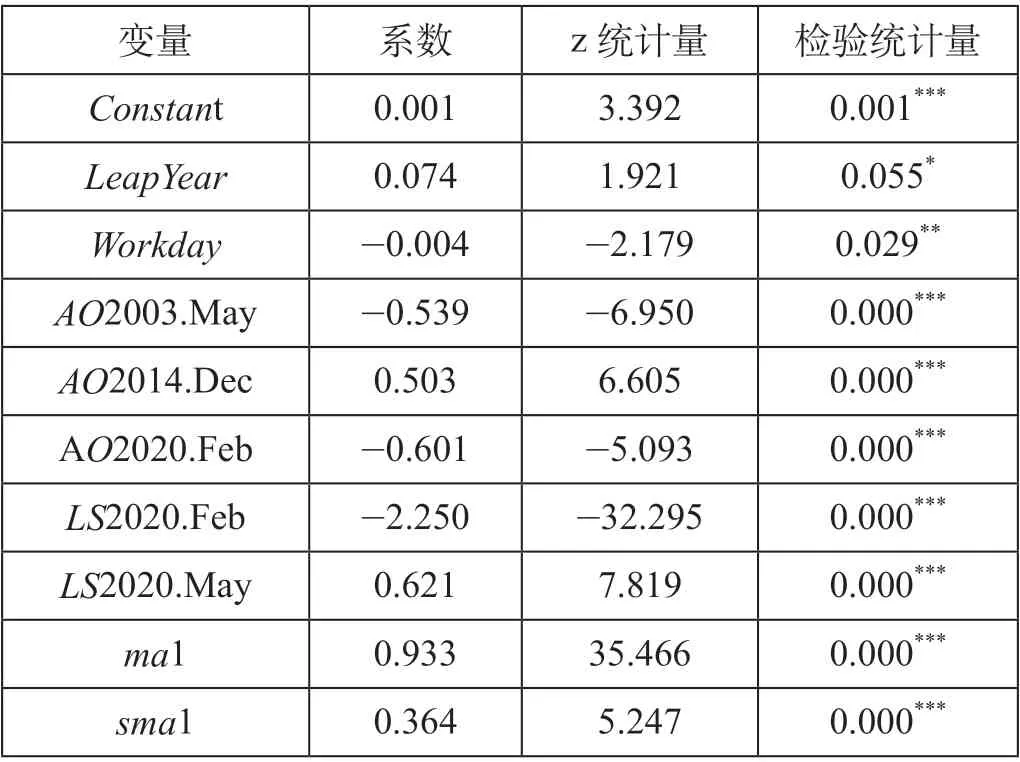
表1 铁路客运量的X-13ARIMA-SEATS 季节调整结果Tab.1 X-13ARIMA-SEATS seasonal adjustment results of railway passenger volume

根据表1 季节调整结果显示，去除季节效应和离群值的最优ARIMA 模型为ARIMA (0，1，1)×(0，1，1)12，残差季节性(QS= 1.021)、相关性(Box-Ljung= 35.00)和正态性检验(Shapiro= 0.975)通过无季节性、无自相关性和正态性检验，模型各个统计量的综合Q统计量为0.740，值小于1，模型有效，该ARIMA 模型可用。模型结果显示，非季节与季节移动平均系数显示强显著性，体现外部环境对铁路客运量影响显著，季节效应显示铁路客运量具有显著的闰年正效应和工作日负效应，检测到影响显著的5 个离群值。根据历年影响铁路客运量的重大突发事件信息，2003 年5 月离群值(AO2003.May)为SARS 疫情对铁路客运量的显著激冷冲击，2014 年12 月离群值(AO2014.Dec)为客票实名制全面实施的政策性显著正向冲击，2020 年2 月离群值(AO2020.Feb，LS2020.Feb)为新冠肺炎疫情初期引起的显著负向冲击，2020 年5 月离群值(LS2020.May)为新冠肺炎疫情解禁令对铁路客运量引起的显著正向冲击。造成冲击的离群值主要分为2 类，一类为突然发生且瞬间变化到某一水平的可加AO离群值，另一类为从某时刻瞬间变化到一个新水平的LS 离群值。在检测到各异常值显著性冲击特征存在的条件下，需要对离群值干预趋势作进一步研究，以分析其冲击变化特点。

2.2 铁路客运量干预模型设计

根据表1 中检测的离群值特点，AO2003.May离群值为2003 年5 月SARS 疫情的暂时冲击，其干预传递函数可以使用公式 ⑽ 表示，考虑其干预减弱趋势，采用具有变化趋势的公式 ⑿ 体现其干预和变化趋势；同理，AO2014.Dec 离群值为2015 年1 月实施的铁路客票实名制政策的前置短暂干预影响，其干预传递函数可以用公式 ⑿ 表示；AO2020.Feb 与LS2020.Feb 离群值为2020 年2 月新冠肺炎疫情对铁路客运量的干预，该干预存在短暂强冲击和后期持续弱冲击，可以采用公式 ⑾ 和公式 ⑿ 的综合冲击函数表示；LS2020.May 离群值干预为2020 年4 月新冠肺炎疫情解禁令实施的长期影响，可以使用公式 ⑾ 表示。将离群值的干预传递函数替换表1 季节调整模型中检测出的离群值变量，作为干预模型中突发事件干预部分。

对于闰年效应和工作日效应，将其作为不需传递变换变量放入模型，其闰年和工作日效应变化借鉴X-13ARIMA-SEATS 闰年效应和工作日效应虚拟变量的构造方式[13]。

相对于表1 中X-13ARIMA-SEATS 季节调整基础模型，该模型不仅能体现离群值代表的突发事件的影响程度大小，更能通过自回归模式显示其突发事件的影响变化过程[14-15]。干预模型算法使用R语言实现[16-17]。

3 铁路客运量干预特征分析

3.1 铁路客运量干预模型分析

根据构建的铁路客运量干预模型(公式 ⒄)，对铁路客运量进行基于表1 最优季节调整模型(ARIMA (0，1，1)×(0，1，1)12) 的干预分析，得到季节调整的干预模型分析结果。铁路客运量干预模型分析结果如表2 所示。根据表2，在模型ARIMA (0，1，1)×(0，1，1)12基础上，添加的各干预变量都表现出强显著性影响，相对模型未添加干预因素的(0，1，1)×(0，1，1)12，该模型AIC值和极大似然估计值分别为-387.93 和205.97，显示出更优的模型拟合效果。

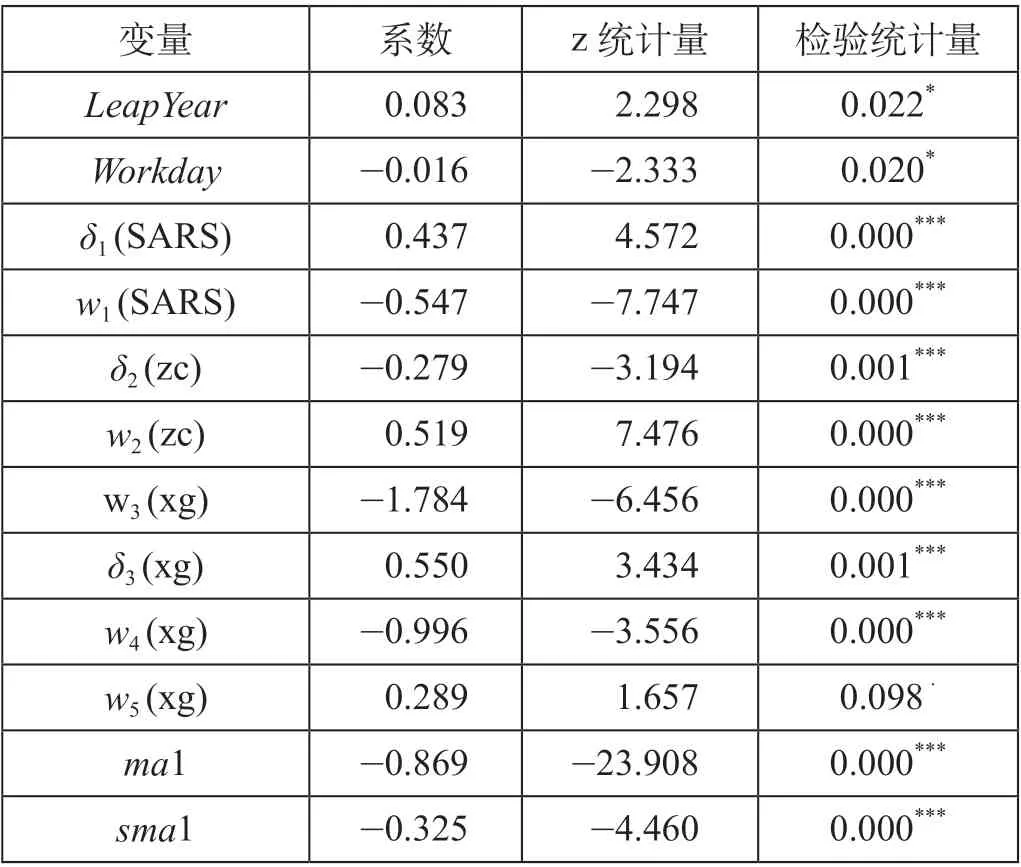
表2 铁路客运量干预模型分析结果Tab.2 Analysis results of intervention model for railway passenger volume

根据表2，闰年效应(LeapYear)和工作日效应(Workday)显著性影响程度变化不大，与季节调整模型结果基本一致；季节(sma1)和非季节(ma1)滑动平均部分系数由表1 中的正显著影响变为负显著影响，体现出客运量本身的外在随机影响因素影响变小；离群值作为干预变量后，以激冷冲击为主的离群值对模型随机部分的负向影响加大，模型体现离群值表征的突发事件对铁路客运量的影响更显著。

3.2 铁路客运量离群值干预影响分析

根据表2，SARS 疫情对铁路客运量表现出显著性负影响，并以0.437p的指数形式逐渐减弱，SARS 疫情在滞后的第2 期显示出较强的恢复趋势，季节与非季节一阶差分铁路客运量离群值干预与恢复趋势比较如表3 所示，在冲击滞后的第5 ～ 6 期铁路客运量基本得到恢复，8 ～ 9期后基本完全恢复，这与智研咨询调查结果基本一致[18]。从2002 年12月SARS 疫情出现初期到2003 年4 月疫情基本控制，铁路客运量未受到很大的冲击，直到2003 年4 月，一些省市(如广东省)取消一系列团体旅行，同时世界卫生组织发出SARS 疫情的全球警告，我国铁路客运量在2003 年5 月(突发期)开始骤然下滑，5 月同比下降61.18%，7 月开始回稳，8 月增速回正，2004 年1 月(滞后8 期)完全恢复。

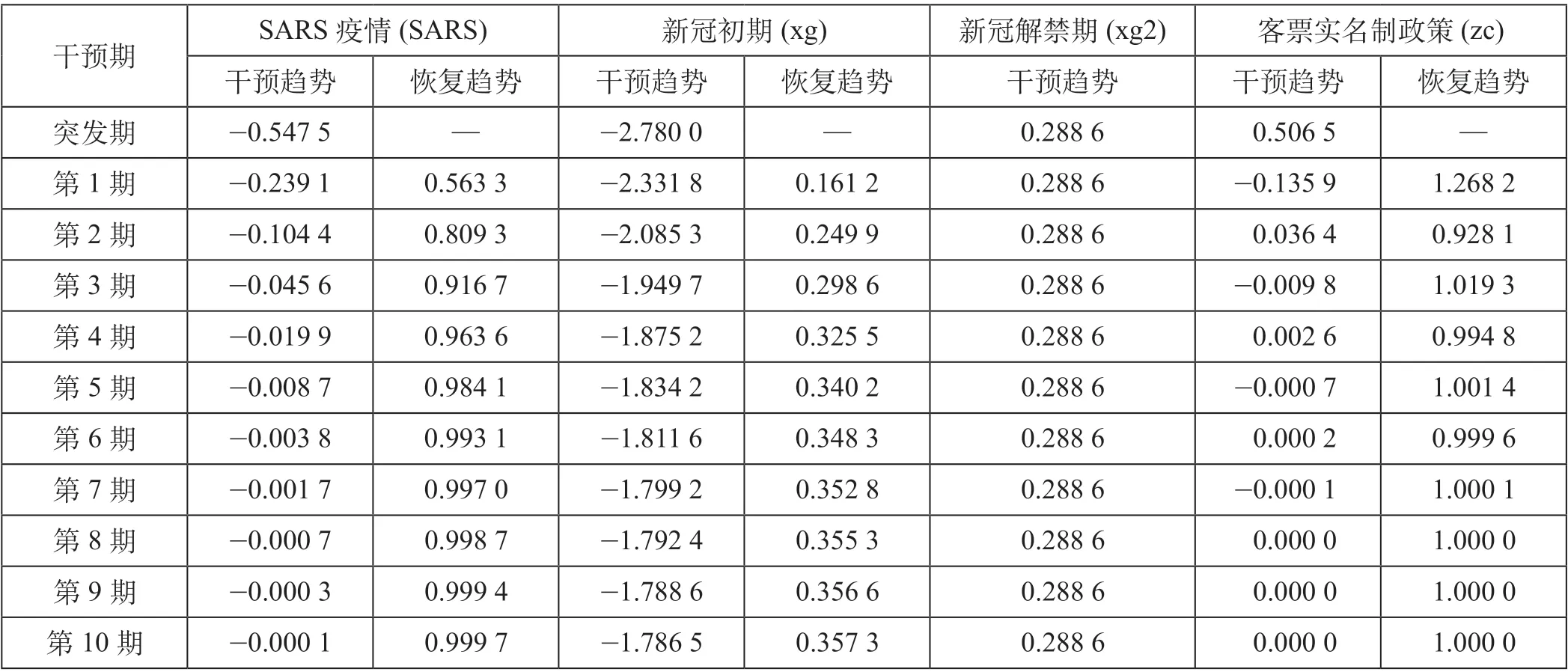
表3 季节与非季节一阶差分铁路客运量离群值干预与恢复趋势比较Tab.3 Comparison of intervention and recovery trend of outliers in seasonal and non-seasonal first-order differential railway passenger volumes

新冠肺炎疫情初期首先对铁路客运量以w3=-1.784 的强永久性显著负影响，同时叠加以w4=-0.996 的显著性负影响，之后以0.550p的指数形式逐渐减弱。根据其恢复趋势，在2020 年12 月(滞后10 期)，疫情初期带来的巨大激冷冲击只恢复到35.73%，疫情解禁令对铁路客运量带来的w5= 0.289的正向永久的显著影响持续存在，与疫情初期影响合并，在2020 年12 月(滞后10 期)，疫情初期带来的巨大激冷冲击恢复到46.12%。

与疫情带来的负向显著影响不同，铁路客票实名制政策对铁路客运量显著性影响是正负波动性逐渐减弱过程，体现出政策具有较强的社会性，在实施过程中还会出现一定的不稳定性，且该政策对客运量影响时间较短。从2015 年1 月1 日全国全面实施铁路客票实名制政策，受政策利空影响，2014 年12 月提前出现铁路客运量大幅增加的激热效应，具体实施实名制后，客运量出现小幅波动，在2015 年3 月(滞后3 期)基本完全恢复，体现出铁路部门前期宣传、试点工作很深入，广大旅客能够很快适应政策的变化。

根据以上分析结果，得到的各离群值干预影响的趋势变化，各种离群值对铁路客运量干预比较图如图2 所示。图2 直观显示出SARS 疫情与铁路客票实名制政策对铁路客运量影响时间比较短，分别在6 个月和4 个月后波动基本趋向为0；新冠肺炎疫情初期影响波动较大，2020 年2 月为冲击最大点，后期开始缓慢恢复，在2020 年4 月解禁令和复工复产等利好政策的推动下，新冠肺炎疫情初期突发性带来的激冷冲击基本完全释放，当前，处于新冠肺炎疫情防控措施和解禁令带来的永久效应影响，这种效应会在较长时间内持续存在。

图2 各种离群值对铁路客运量干预比较图Fig.2 Comparison chart of various outliers intervening railway passenger volume

3.3 铁路客运量趋势预测分析

对季节调整模型与基于离群值特征的干预模型拟合值进行相对误差比较分析，季节调整模型与干预模型绝对相对误差比较如表4所示。分析结果显示，干预模型绝对相对误差相对季节调整模型低10%，显示干预模型拟合结果与实际值更接近，对数据的拟合更有效。因此，将离群值作为干预变量进行分析能够提高铁路客运量的拟合精度。季节调整曲线、干预模型拟合曲线与原始曲线比较如图3 所示。

根据图3，季节调整曲线消除各类季节效应的影响，调整曲线相对原始曲线光滑很多，可以较为客观地体现铁路客运量的整体发展趋势；干预模型拟合曲线与原始曲线基本重合，可以更好地体现干预模型对铁路客运量的信息解释程度。在当前新冠肺炎疫情管控条件下，疫情对铁路客运量冲击在逐渐减小，铁路客运量逐渐回暖，总体处于上升趋势。

4 结束语

研究基于SARS、新冠肺炎疫情和铁路客票实名制政策等主要干预事件构建我国铁路客运量干预模型，从干预理论和可视化过程2 个方面分析突发事件的冲击过程，在一定程度上能够厘清突发事件对我国铁路客运量干预的发展趋势，该方法可以拓展到我国交通系统突发事件干预的多个方面。在实际研究过程中，由于数据的不可获得性，没有考虑铁路线路增加和区域特点对铁路客运量的影响，在不影响整体发展趋势的条件下一定程度上会弱化或强化突发事件干预因素的干预强度，这也是当前不能深入进行这方面干预分析的难题所在。