长江流域海铁联运模式下港口集疏运物流网络研究
李安林,魏海蕊
(上海理工大学 管理学院,上海 200093)
0 引言
我国2016 年审议通过的《长江经济带发展规划纲要》(以下简称《纲要》),标志着我国长江流域地区进入经济高质量发展的新时代[1]。《纲要》提出要加快建立长江流域综合立体交通走廊,以优化区域各要素配置,扩大对外开放,构建开放型经济体制。构建低成本、高效率的物流网络能有效降低长江流域地区进出口贸易的物流成本,增加进出口贸易量,提升地区对外开放水平。
目前,我国港口集疏运的主要方式仍以公路为主;海铁联运模式将出口货物以集装箱形式,由铁路从内陆腹地的无水港运到沿海港口再经船舶运至境外,为港口集疏运提供新运输模式的选择[2];随着集装箱运输规模的扩大以及产业经济向我国中西部地区的转移,进出口货物的规模及集疏运距离在逐渐增加,相较于公路运输,铁路运输在运输距离较长、货运量较大时具有更大的优势。关于海铁联运物流网络的优化研究方面,齐颖秀等[3]提出以货运代理为主导的海铁联运全程物流服务方案以解决联运服务过程缺乏统筹协调的问题;汤银英等[4]基于多式联运网络,考虑到不同运输方式的最大承载能力及铁路班列的发车班期,构建了最小运输成本、最短运输时间的多目标整数规划模型,并求解得到不同发车情形下的最优联运方案;Li 等[5]利用IFTN 模型将多式联运货物运输的整数规划问题转化为集装箱流量控制问题,以解决深海码头与内陆码头之间的多式联运货物运输规划问题;Resat 等[6]建立以运输成本和时间最小化为目标的混合整数规划模型,以优化土耳其马尔马拉地区工业产品的多式联运物流网络。
通常,铁路运输的单位成本随货运量的增加而降低,当城市货运需求不同时,城市物流模式的选择存在差异;同时,当各城市的货物汇集到枢纽城市后,由于货运量的增加,物流集成商会优先采用海铁联运模式进行集运。因此,引入铁路运输规模成本函数,在考虑铁路规模效益的基础上应用复杂网络和数学规划等方法,研究建立长江流域海铁联运物流网络框架,以优化该地区的货流组织,降低物流成本。
1 海铁联运物流网络概述
海铁联运物流网络分为港口的铁路集疏运网络和跨境海运网络2 个主要部分,对于我国的进出口货物而言,无论其是采用海铁联运集疏运模式或是公路集疏运,其装箱后到运至目的地间的海运成本是相同的,因此将海铁联运网络构建的重点放在各港口的集疏运网络的构建上。海铁联运的实现需要内陆地区构建物流中心,以完成对货物的单证办理、检验检疫及换装工作,为此将构建轴辐式海铁联运物流网络,选择重点物流城市作为轴辐式网络的枢纽节点并构建物流中心,各节点的货物在枢纽城市集散、换装,完成运输模式上的转换。
腹地城市i有一批货物需经海运运输至目的地,现假设从城市i集运到港口p有4 种方式可以选择:①通过公路运输集运至港口;②通过铁路直接运输至港口作业区,实现海铁联运;③先通过公路运输至枢纽城市,货物经枢纽城市集结、换装后,以海铁联运的方式运至港口;④先通过铁路运输至枢纽城市,货物经枢纽城市集结、换装后,以海铁联运的方式运至港口。海铁联运物流网络模式如图1 所示。
2 考虑铁路规模效益的海铁联运物流网络模型构建
2.1 基于复杂网络的枢纽城市选择
为保证腹地城市能与枢纽城市的连通效率最大化,应选择在物流网络中具有较高物流连通性的城市作为枢纽城市,而复杂网络的中心性理论正是衡量网络中各节点连通性与重要性的指标[7]。城市物流连通性指标体系的构建由度中心度、中间中心度、接近中心度和特征向量中心度4 项指标构成,并利用熵权法求取各项指标的权重,以获得各城市的物流连通性强度。
其中各项指标的具体含义如下。
(1)度中心度。节点i的度中心度为与之相连的其他节点个数,当节点i的度中心度越大,代表其在整个网络中影响力越大。
式中:DCi为节点i的度中心度;di为与节点i相邻的节点个数;n为总节点个数。
(2)接近中心度。节点i的接近中心度是其到达网络内其他节点的最短距离之和,接近中心度越大,代表节点i到达其他节点较为容易,该指标计算公式为

式中:CCi为节点i的接近中心度;dij为以节点i为起点,节点j为终点的最短路径包含边的数量。
(3)中间中心度。假设网络中存在一对节点j和k,j和k之间存在多个最短路径,节点i的中间中心度定义为经过节点i的两点间最短路径数量占最短路径总数之比;中间中心度越高,代表了节点i在网络中的中介作用越强,该指标的计算公式为

式中:BCi为节点i的中间中心度;pjk(i)为经节点i且连接节点j与k之间最短路径的数量;gjk代表节点j与k间最短路径总数。
(4)特征向量中心度。特征向量中心度是度量网络中节点重要性的指标,当节点i的特征向量中心度较高时,代表节点i与网络中很多重要的节点相连,该指标的计算公式为

式中:ECi为节点i的特征向量中心度;λ为比例常数;aij为邻接矩阵中对应第i行j列的数值;xj为节点j的度中心度。
熵权法的评价过程不受主观因素影响,适用于不包含主观判断指标的加权分析。各指标权重的计算方法为
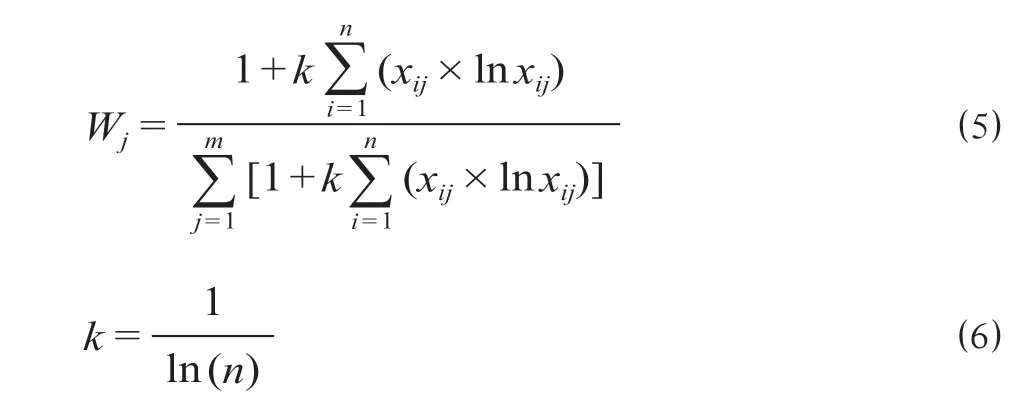
式中:Wj为第j项指标的权重;xij为节点i的第j项指标标准化后的数值;k为权重参数;m为选取的指标数量。
运用收敛相关算法基于各城市在物流网络中的连接关系结合物流连通性强度对枢纽城市进行筛选。收敛相关是复杂网络理论中的分类算法,该算法首先建立各节点的连接关系矩阵,其次通过计算连接关系矩阵中各行的相关关系系数,组成新的相关关系矩阵,并依此方法进行迭代,最后根据密度表可以得到各节点的分类情况[8]。该方法可以保证各枢纽城市的均匀分布,避免枢纽城市过于集中,同时提高筛选的效率。利用收敛相关算法对所有城市进行分类,并在每一类城市群中选择出物流连通性强度最高的城市作为枢纽城市。
2.2 基于整数规划模型的海铁联运物流网络构建
基于筛选出的枢纽城市,在考虑铁路运输规模成本的基础上建立以运输成本最小化为目标的0-1整数规划模型,以此来构建各腹地城市、枢纽城市和港口城市间海铁联运物流网络。
2.2.1 公铁联运规模成本函数
铁路运输行业的规模经济指铁路运输的平均运输成本随运输货运量的增加和运输能力的提升而下降的现象,单纯的线性成本函数无法真实反映铁路运输的实际成本,在现实中货主的货物仍需要卡车进行短驳后运至当地的铁路货运站。运用米兰· 亚尼克开发的公铁多式联运综合成本计算模型研究物流网络构建问题[9],具体参数及公式含义如下。
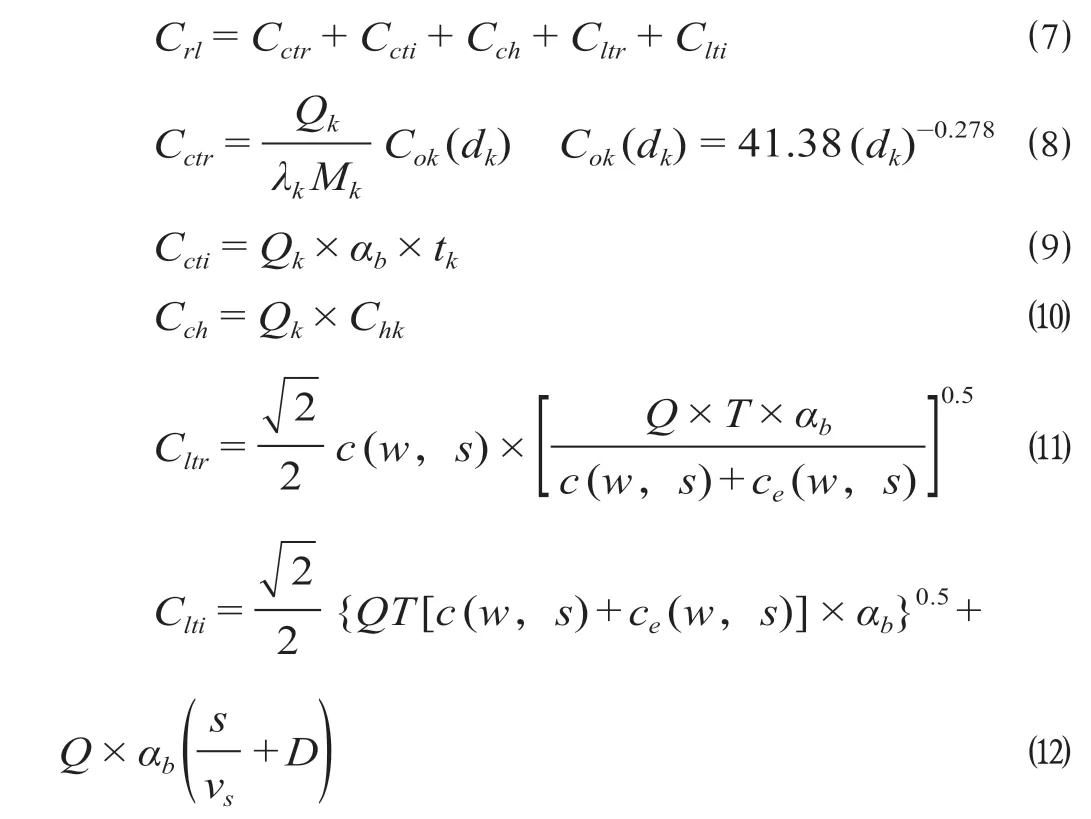
式中:Crl为货物从货主处运至港口的公铁联运总成本,元;Cctr为货物运至多式联运中心的卡车驳运成本,元;Ccti为货物运至多式联运中心的时间成本,此处将货物运输过程中因贬值或资金占用而产生的时间损失转化为金钱进行度量,元;Cch为装卸成本,元;Cltr为多式联运中心至港口的铁路运输成本,元;Clti为多式联运中心至港口的运输时间成本,元;Qk为货运量,t;λk为荷载系数;Mk为卡车的承载能力,t;Cok(dk)为将货物运至多式联运中心的卡车驳运单位运输成本,元/车;dk为卡车平均驳运距离,km;αb为时间成本率,将运输过程中消耗的时间转化为金钱进行度量,单个集装箱的时间成本率为0.385 元/h[10];tk为公铁联运总运输时间,h;Chk为装卸费率,参考铁路运输费用设置标准[11],此处Chk的取值为39.25 元/t;T为列车在单个周期内(7 d)的运营时间,T取值120 h 即5 个工作日,c(w,s)和ce(w,s)分别代表铁路内部与外部运输成本,是一个与运输距离s和运输总量w有关的函数[9],这2 项成本的表达式分别为4.44 (ws)0.74和4.37 (ws)0.689;vs为列车平均运行速度,km/h;D为列车途中作业的平均延误时长,据调查其约为0.5 h。
2.2.2 数学规划模型的建立
为构建各腹地城市与枢纽城市及港口的运输关系,在考虑各枢纽城市铁路运输规模效益的基础上,以物流网络运输成本最小化为目标构建整数规划模型,模型具体如下。

公式 ⒀ 表示目标函数使总运输成本最小;公式 ⒁ 表示不经枢纽转运时的总物流成本;公式 ⒂表示经枢纽转运时的物流成本;公式 ⒃ 表示枢纽处的运输规模成本;公式 ⒄ 表示对于任意的腹地节点i只可以选择一条运输路线将货物运输至港口城市;公式 ⒅ 表示各枢纽城市所接受的货物数量不应超过该枢纽的承载力上限;公式 ⒆ 表示限定各决策变量只能取值为0 或1。
3 长江流域城市海铁联运物流网络实证分析
3.1 重点物流城市及港口选择
依据商务部等10 个部门联合印发的《中国流通节点城市布局与规划(2015—2020)》,选择国家级物流节点城市如重庆、武汉等,以及长江流域铁路干线交汇处的城市,如徐州、鹰潭等共15 个城市作为重点城市。对于港口城市的选择,则主要考虑港口铁路站与码头堆场的衔接问题。目前我国大部分港口仍需要集卡将货物驳运至码头堆场,因此选择铁路与海运可以无缝对接的连云港港、宁波舟山港和深圳港作为海铁联运物流网络的出海港口[12]。
3.2 基于复杂网络的枢纽城市选择
考虑到枢纽城市应具有较高的物流连通性,构建各节点城市间的铁路运输连接关系如图2 所示。同时测算了各节点城市的各项中心性指标,并通过熵权法对所得结果进行加权计算,计算得到度中心度、接近中心度、中间中心度、特征向量中心度的权重分别为0.1,0.02,0.77,0.11;并得到各节点的物流连通性强度。各港口及节点城市的物流连通强度如表1 所示。
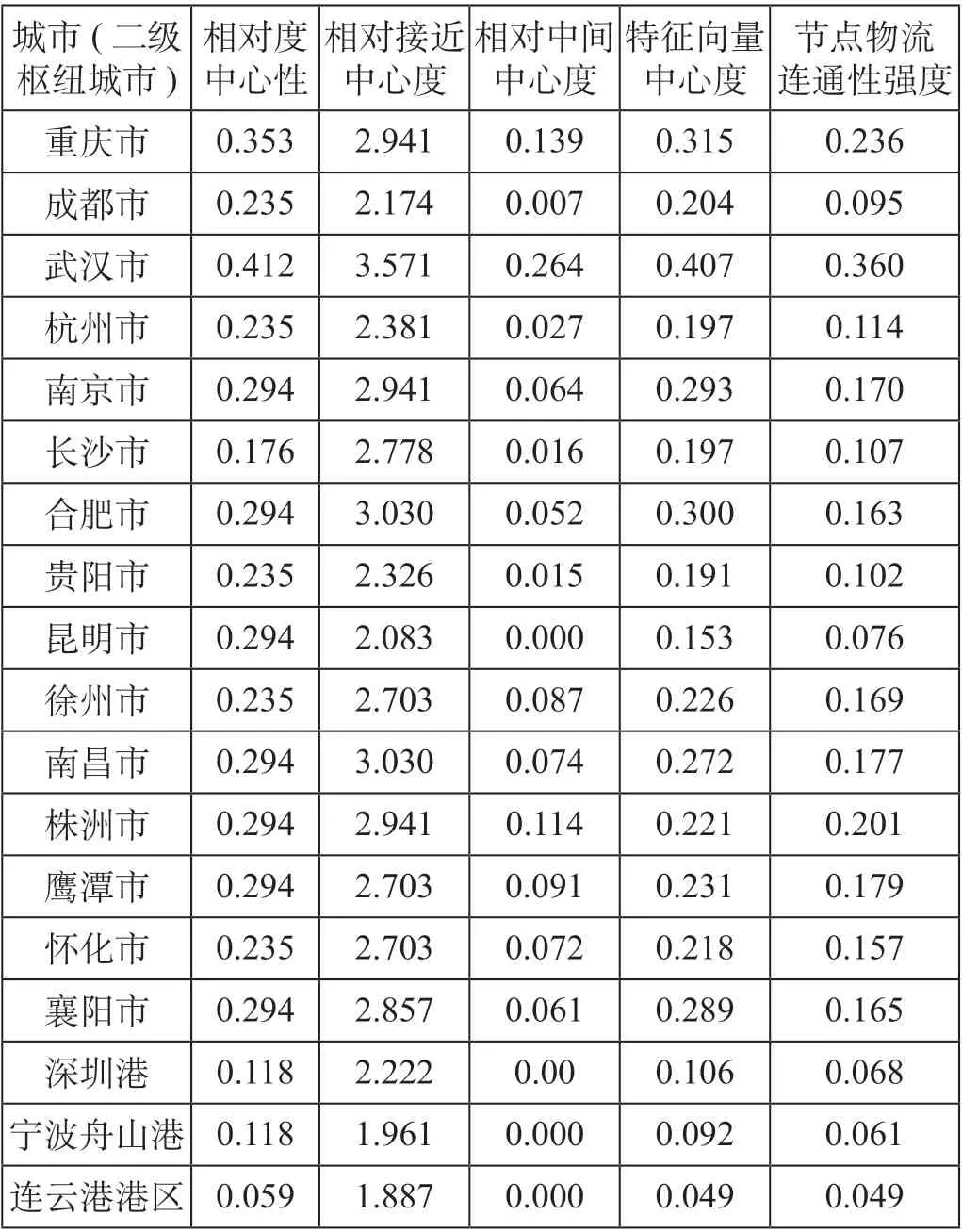
表1 各港口及节点城市的物流连通强度Tab.1 Logistics connectivity index of each node and port city
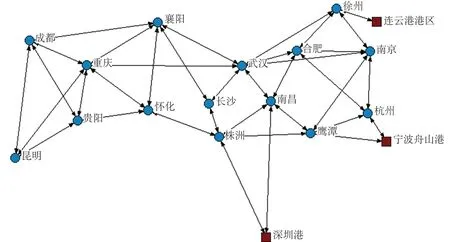
图2 各节点城市间的铁路运输连接关系Fig.2 Railway connection between node cities
通过收敛相关算法依据各城市间的连接关系对其进行分类,收敛相关算法分类结果如表2 所示,重新排列迭代完成后的相关关系矩阵,得到了各城市间的关系密度表,所有城市依据它们之间的关系密度被分成5 个子群;同时依据复杂网络的中心性原理构建的物流连通性指标,得到每组城市子群中连通性最高的城市作为枢纽城市,分别为株洲市、重庆市、鹰潭市、武汉市和南京市。
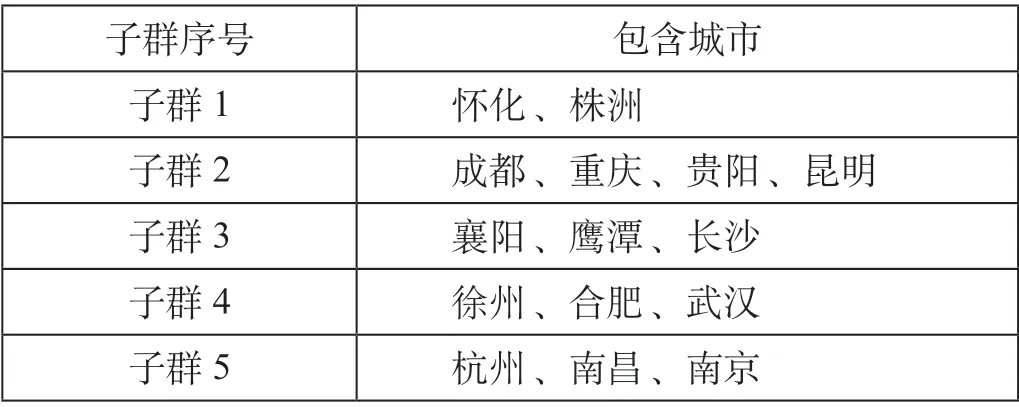
表2 收敛相关算法分类结果Tab.2 CONCOR algorithm classification results
3.3 海铁联运物流网络建立
求解规划模型以建立海铁联运物流网络,各腹地城市的出口货物量数据来源于各地市的统计公报,铁路运输周期设为7 d/班;公路货运单位成本为0.3 元/(t·km)[13];模型的求解使用模拟退火算法,求解得到模拟退火算法迭代图如图3 所示,经多次迭代后,获得整个网络每年的运输成本的近似最优解为11.779 亿元。物流网络图如图4所示,连云港港口主要接受以南京作为枢纽城市的江苏、安徽地区的货物,这与现实情况相同;而武汉作为湖北地区的枢纽之所以放弃上海港而选择连云港港的主要原因是上海的洋山港与外高桥港没有铁路进港的条件,出口集装箱需先运至芦潮港和杨浦港,再经卡车驳运才能进入港区[14],港口堆场与铁路无法做到紧密衔接。宁波舟山港主要吸引浙江地区和江西地区的货物,与湖北地区相同,以鹰潭为物流枢纽的江西地区没有选择福州或厦门港出海,也是因为铁路港口站与码头后方堆场无法做到直接换装。深圳港将作为四川、重庆、湖南、贵州和云南地区的出海港口,其中重庆作为枢纽城市集结并换装成都地区的货物,株洲则集结并换装长沙、怀化和贵阳地区的货物后通过铁路运输至深圳港出海,昆明则通过铁路运输至深圳港。
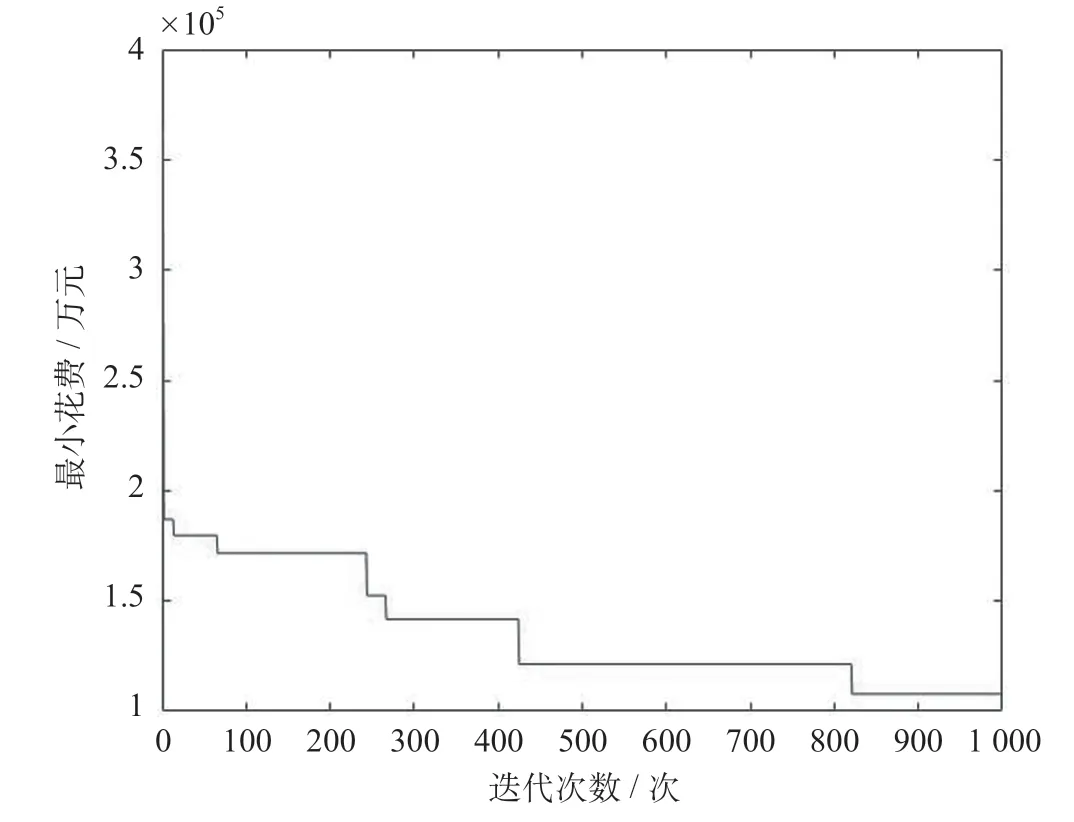
图3 模拟退火算法迭代图Fig.3 Simulated annealing iteration graph
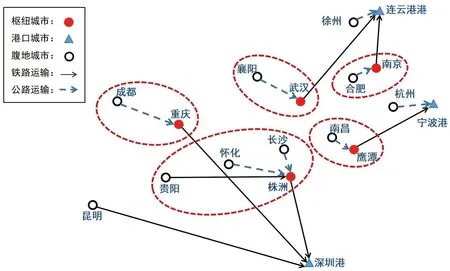
图4 物流网络图Fig.4 Logistics network diagram
3.4 铁路运输规模效益对物流网络的影响
为探究铁路运输的规模效益对成本的影响,计算了当不通过联运枢纽而直接运输至港口时各城市的运输成本,并得到不同运输模式下的运输成本及铁路运输占比如表3 所示。通过海铁联运枢纽运输时,铁路货运量占总货运量的70.37%,高于不通过联运枢纽时的49.21%,而总运输成本只占不通过联运枢纽时的80%,多式联运枢纽对货物的整合作用能有效提升枢纽城市的货物运输规模,当货物规模提升时,铁路运输的优势得以展现,降低总体运输成本。
为进一步探究货物规模的影响,计算了不同货运规模下的单位运输成本如表4所示。海铁联运模式下的运输成本在运输距离不变的情况下随着运输规模的提升而显著降低,并且其下降幅度大于不存在枢纽时的成本降低。由于多式联运枢纽的存在使枢纽城市的货运规模提升,海铁联运模式下铁路运输的占比较高,因此随着货物规模的提升其单位成本下降的速度也更快,构建物流网络以引导货流经合适的联运枢纽转运,可以最大化地发挥铁路运输的规模效益。

表4 不同货运规模下的单位运输成本 元/ tTab.4 Unit transportation cost under different freight scale
铁路枢纽城市对货物的整合作用使货运的规模提高,进而获得了规模效益、降低了部分物流成本。因此,相较于各城市单独将货物运输至港口的运输模式而言,通过建立海铁联运物流网络来引导货物通过枢纽城市整合后运至港口城市的物流模式可以有效降低运输成本;且随着货运规模的逐步增加,海铁联运模式下的单位运输成本有更大幅度的降低,这意味着在拥有更大货运规模时,海铁联运模式将获得更大的规模收益。
4 结束语
构建高效、低成本的海铁联运物流网络是保证长江流域地区新经济体制构建与经济高质量发展,完善综合立体交通走廊建设的重要手段之一。通过复杂网络中心性理论评估长江流域城市的物流连通性强度,利用收敛相关算法选择枢纽城市,并构建了以成本最小化为目标的考虑铁路运输规模效益的整数规划模型,得到以南京、武汉、重庆、鹰潭、株洲为枢纽的海铁联运物流网络。经实例验证,铁路单位运输成本随运输规模和运输距离的提升而降低;相比各城市单独运输,构建海铁联运物流网络可有效降低物流成本、提升铁路运输规模,促进铁路运输行业的发展。今后应考虑到不同品类货物时间敏感性的差异,对货物进行细分,对不同品类货物的物流运输模式展开研究。

