基于EMB的纯电动汽车制动能量回收优化控制策略研究*

常九健，张煜帆

（1.合肥工业大学智能制造技术研究院，合肥 230000；2.合肥工业大学汽车与交通工程学院，合肥 230000）

前言

随着科技进步和社会发展，汽车保有量逐年递增，石油、煤炭、天然气等不可再生能源的需求急剧增长，带来了能源消耗和环境污染等问题。纯电动汽车以其结构简单、噪声小、零排放的特点备受世界关注，另外电动汽车可以进行制动能量回收，从而提高整车能量利用率、弥补续航里程不足问题。作为新能源汽车研究的新方向，电子机械制动（EMB）系统反应灵敏，制动效能高，结构简单，易于和其他系统进行综合控制，且可大幅提升整车的能量利用率，近年来受到了广泛关注。

汽车的再生制动控制策略也不断发展，有固定比例的分配策略、神经网络控制策略和遗传算法控制策略等。但是对基于EMB 系统的制动能量回收控制的研究还很少。本文中提出了一种在电子机械制动的基础上，采用PSO 算法优化模糊控制的制动能量回收控制策略，以最大化回收能量为目标，对模糊控制进行优化。再通过Simulink 和AVL Cruise 联合仿真进行验证。结果表明，所采用的策略增加了回收的制动能量。

1 电子机械制动系统

1.1 电子机械制动系统的工作原理

EMB 系统由EMB 控制器和EMB 执行器两部分组成。其中，EMB 执行器包括驱动电机、减速增转矩装置和运动转换机构3 个部分；而EMB 控制器作用是控制电机的转动，运动转换机构作用是将旋转运动转变为平移运动，使经过减速增转矩装置的力矩转换成推动制动盘垫片的压紧制动力，从而达到制动的效果。

1.2 电子机械制动系统模型

EMB 系统采用压力-转速-电流三闭环控制。内环是电流控制环，输入为转速控制环所输出的目标电流与实际电流的差值；外环为压紧力控制环，输入为目标制动压紧力与反馈制动压紧力的差值，如图1所示。

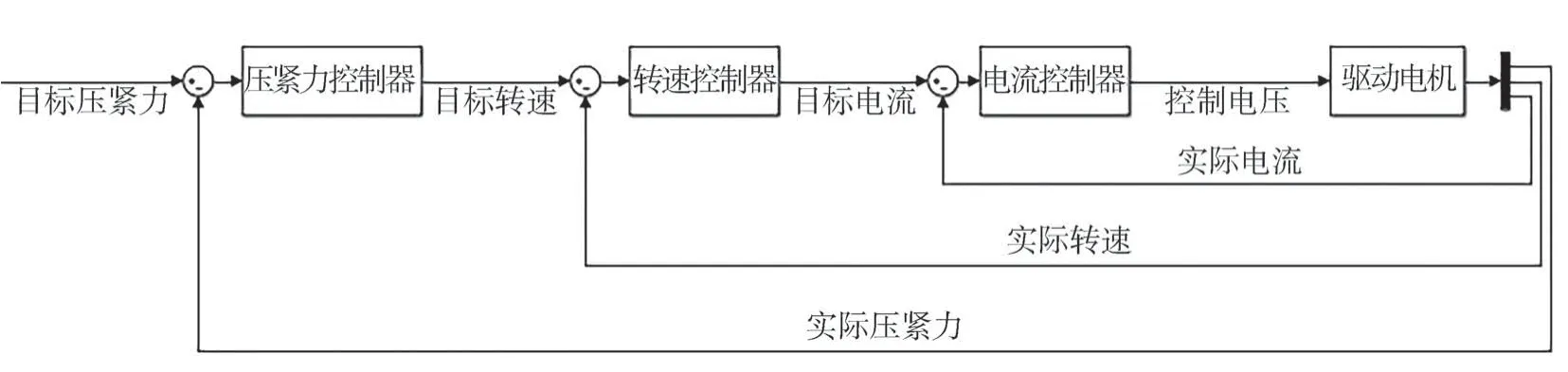
图1 压力-转速-电流三闭环控制

1.2.1 永磁同步电机数学模型

永磁同步电机（PMSM）是一个非线性、多变量的系统，经过坐标变换后，即可转化为在坐标系下的数学模型。

PMSM电压方程为

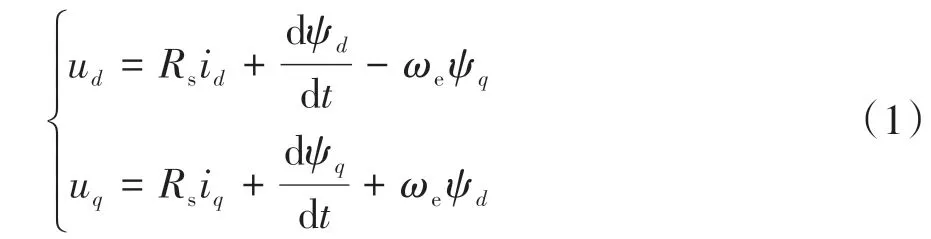
式中：u、u为定子电压在轴上的分量；i、i为定子电流在轴上的分量；ψ、ψ为定子磁链在轴上的分量；=为转子的电角速度，为电机极对数，为转子机械角速度；为定子绕组的电阻。

磁链方程为

式中：L、L为定子绕组在轴上的电感分量；为永磁体磁链。

PMSM机械特性如下：

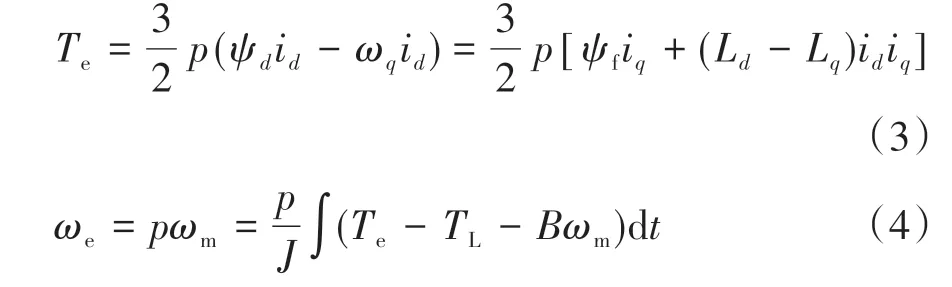
式中：为转动惯量；为摩擦因数；为负载转矩；为电磁转矩。

综上得到计算电机轴电流和机械角速度的微分方程为

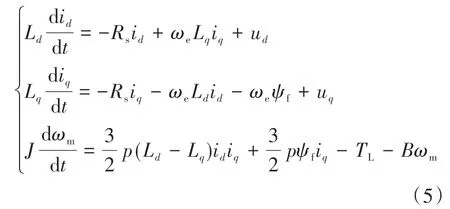
通过上式建立电机参数模型，u、u、为输入，计算电机i、i、转速、转矩、转角。

1.2.2 行星齿轮减速机构数学模型

式中：为行星架输出转矩；为太阳轮的输入转矩；为传动比；为行星齿轮的传动效率。传动比过小，电机的尺寸较大，空间难以满足要求，传动比过大，行星齿轮发热严重，经过对比，本文选定传动比为5.503。

1.2.3 滚珠丝杆副数学模型

式中：为滚珠丝杆的驱动转矩；为丝杆推力；为丝杆导程；为滚珠丝杆的传动效率。

2 再生制动控制策略

2.1 前后轴制动力分配和电机机械制动力分配

在制动时，前后轮同时抱死，此时前后轴制动力F、F分配关系对应的曲线称为I 曲线，而F与F的关系式为

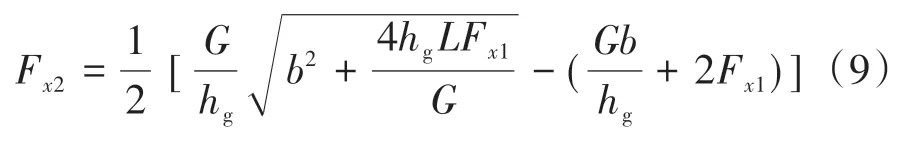
同时参考联合国欧洲经济委员会制定的ECE R13 制动法规，为保证制动时汽车有足够的制动效率和稳定性，对双轴汽车的前后轴制动器制动力提出了明确的要求：

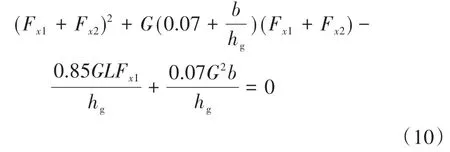
式中：F为前轴制动力；F为后轴制动力；为汽车质心高度；为前轴到后轴的距离；为后轴到质心的距离；为汽车重力。

同时，制动力矩和制动压强之间存在关系为

式中：为当前汽车所需的制动转矩；为当前汽车机械制动器所需的制动压强；为制动缸活塞的面积；为制动器制动效率；为制动器摩擦因数；为制动盘的有效摩擦半径；为制动器特定因素，是一个取决于制动器设计的因素。对于盘式制动器，取1，对于鼓式制动器，通常大于1。

制动强度为

式中：为整车质量；为车轮半径。

前后轴制动力分配曲线如图2所示。

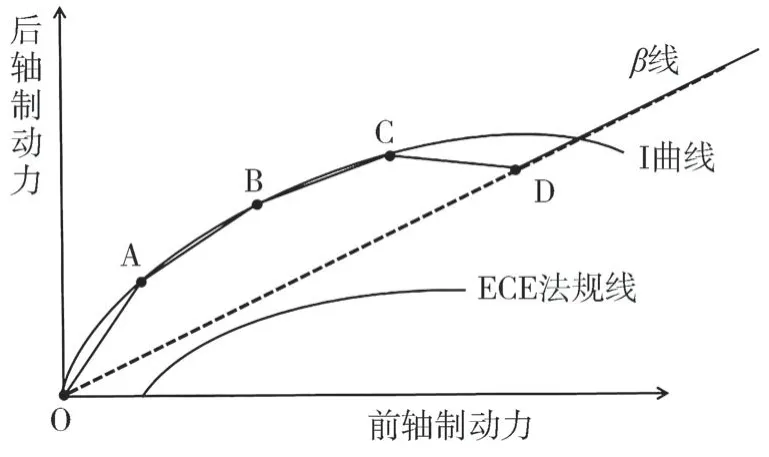
图2 前后轴制动力分配

I曲线上已知制动强度的点满足式（13）。

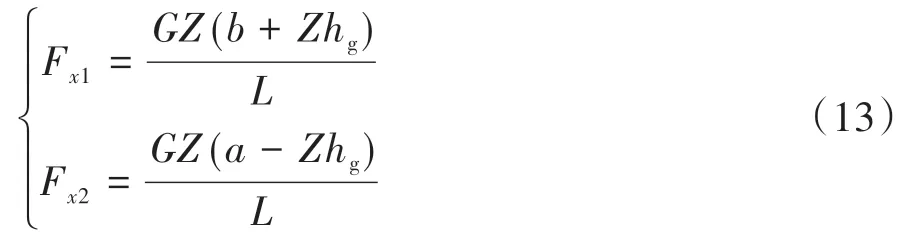
O 为原点，A 是I 曲线上制动强度0.2 的点，按式（13）算得点A 在图2 中的坐标F，F，此时OA 线段的斜率为=F/F，得线段OA 上制动力分配为

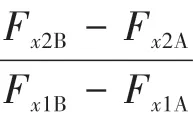
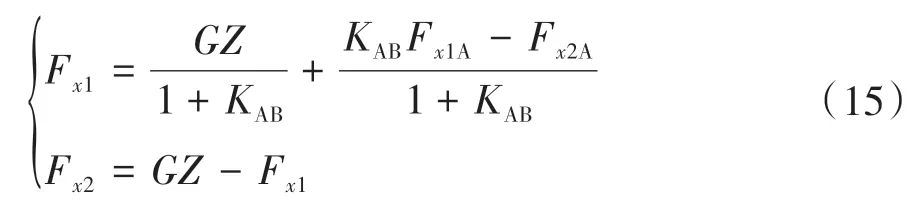
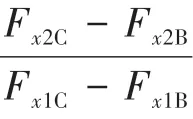
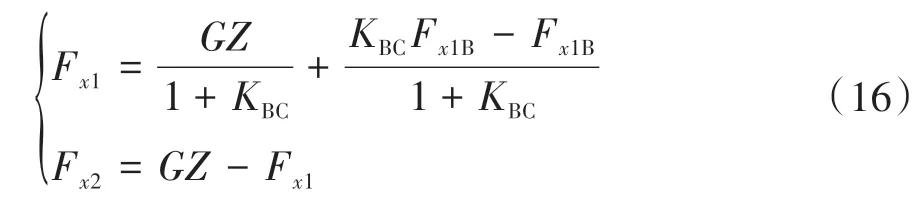
D 是线上制动强度＝0.75 的点，线上已知制动强度的点满足式（17）。

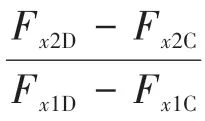
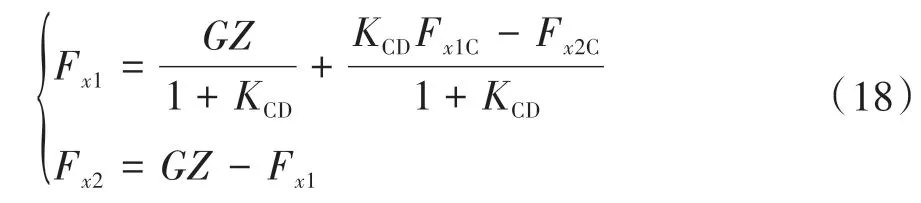
当制动强度＞0.75 时，认为是紧急制动，退出再生制动模式，为保证紧急制动时前后轴能够迅速精准分配，前后轴制动力分配按照线分配：

2.2 再生制动模糊控制器设计

模糊控制是一种智能控制，主要用来解决复杂非线性问题。模糊控制器基本结构见图3。

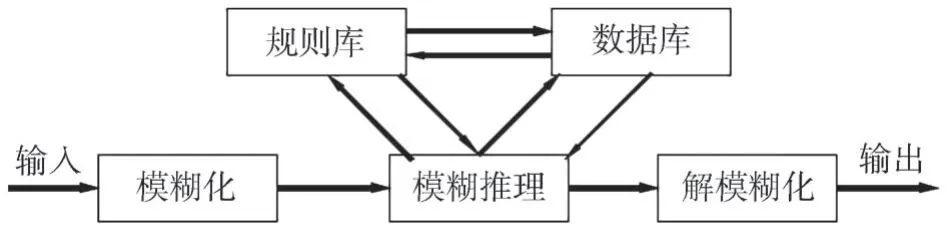
图3 模糊逻辑控制器结构

2.2.1 输入输出变量选择

该控制器3 个输入量分别为制动踏板行程（%）、电池的（%）和车速（km/h）。输出量是再生制动占比系数。通过制动踏板行程，根据AVL Cruise 软件中制动踏板行程与制动压强的关系，再结合式（11）可算出车辆需求的制动转矩、车速和电池的SOC值同样影响电机的再生制动转矩。

2.2.2 输入模糊化

采用Mamdani 推理方法。制动踏板行程（%）的模糊论域设置成［0，100］，相对应分成3 个模糊子集｛高（G），中（Z），低（D）｝；电池值（%）的模糊论域设置成［0，100］，相对应分成3 个模糊子集｛高（G），中（Z），低（D）｝；车速（km/h）的模糊论域设置成［0，140］，相对应分成4 个模糊子集｛高（G），中（Z），低（D），很低（HD）｝。

2.2.3 输出反模糊化

输出量是再生制动占比系数，取其模糊论域为［0，1］，分为5 个模糊子集｛很高（HG），高（G），中（Z），低（D），很低（HD）｝。

2.2.4 模糊控制规则

制动踏板行程越大，表示制动需求越大，为保证安全，再生制动占比应减小；电池值越大，为防止过充，保护电池寿命，再生制动占比应减小。由此制动模糊控制规则如表1所示。

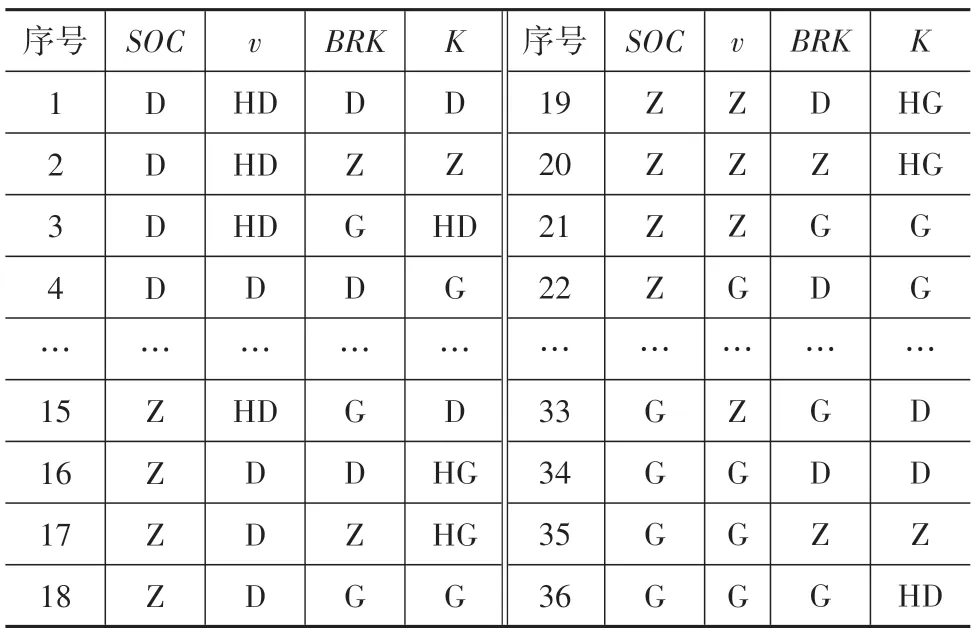
表1 模糊控制规则

2.3 PSO算法对模糊隶属度函数的优化

粒子群算法是从鸟类族群觅食的讯息传递所得到的一个启发，族群中的每只鸟都相当于一个粒子个体，它们有自己的记忆，通过移动产生记忆积累经验，并依此调整自身的移动方向和速度。多个粒子同时移动，且相互学习经验，由此相互比较得到最优解，同时整个群体拥有学习性、记忆性，从而也影响粒子达到最佳状态。

模糊控制设计简单，便于应用，且鲁棒性强，适应于非线性时变系统。但由于模糊控制的隶属度函数和模糊控制规则往往依据经验而不够准确，无法获得全局最优。而粒子群优化（PSO）算法是一种结构简单、收敛速度较快且能在个体与社会性之间寻求平衡的随机全局优化算法，可以提高模糊控制的准确性。将需要优化的参数设置为｛，，…，，｝。设置最大迭代次数为50，每代的粒子数量为20个，粒子的最大速度为0.1 m/s。以最大化制动回收能量为目标函数进行优化。优化前的隶属度函数如图4所示，优化后的隶属度函数如图5所示。

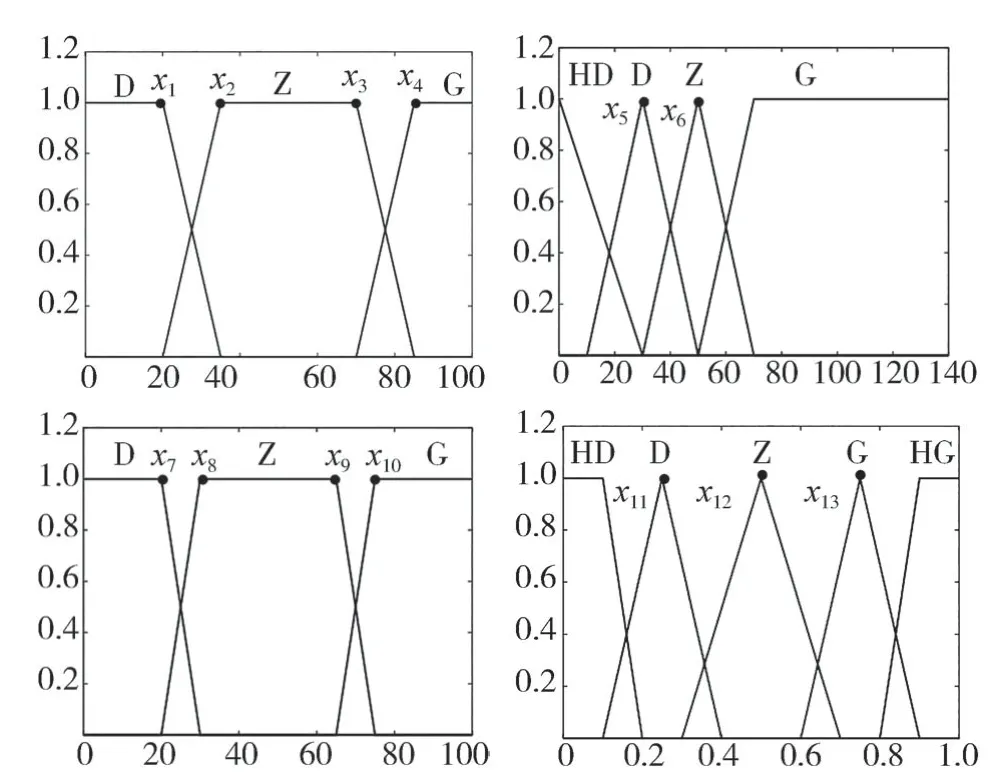
图4 优化前模糊控制隶属度函数图

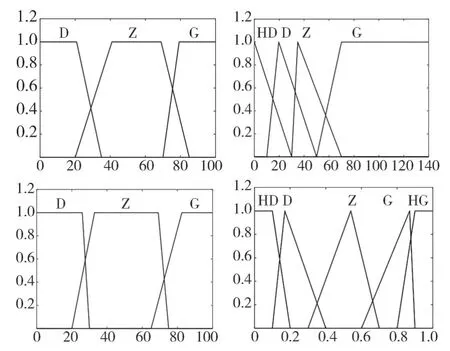
图5 优化后模糊控制隶属度函数图

2.4 约束条件

2.4.1 电机转矩特性限制

采用4 个永磁同步电机，当电机转速低于额定转速时，电机处于恒转矩阶段，最大制动转矩为；当电机转速高于额定转速时，电机处于恒功率阶段。轮毂电机最大再生制动力为

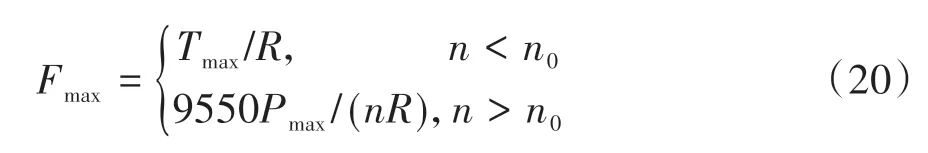
式中：为电机能提供的最大再生制动力，N；为电机提供的最大转矩，N·m；为车轮半径，m；为电机转速，r/min；为电机额定转速，r/min；为电机最大功率，kW。

2.4.2 电池SOC的限制

为保护电池，防止电池过充，当＞85%时，就应退出再生制动模式，转为纯机械制动。

2.4.3 汽车车速的限制

当汽车车速很低时，电机转动很慢，产生的充电电流很小，为使车辆尽快停车，当车速低时退出再生制动模式，转为纯机械制动。本文设置限制车速为5 km/h，当车速低于该值，便退出再生制动。同时为使再生制动和机械制动的交替平缓进行，设置一个速度影响因子K：

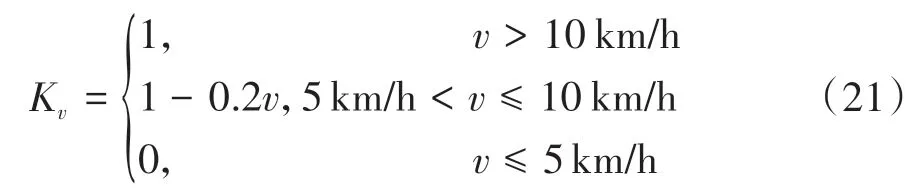
最终的电机再生制动力占比系数为K×K。电机的再生制动力等于分配到每个轴上的需求制动力乘上约束后的占比系数K×K。经过前后轴制动力分配得到前后轴的需求制动力，然后检测每个轴的再生制动力是否能够满足需求，如果不能，则利用机械制动力作为补充。

2.5 再生制动过程分析

收到驾驶员制动信号后，根据式（12）计算制动强度，同时根据当前车速和电池值判断是否进行再生制动。若不符合条件，结合图2，得到前后轴需求制动力，利用EMB 系统进行纯机械制动。若符合条件，结合图2，得到前后轴制动力，再输入模糊控制器，得到所需再生制动力，同时与轮毂电机最大再生制动力进行比较：如果大于，则完全由电机提供制动力；如果小于，则利用EMB 系统进行补充。整个流程见图6。

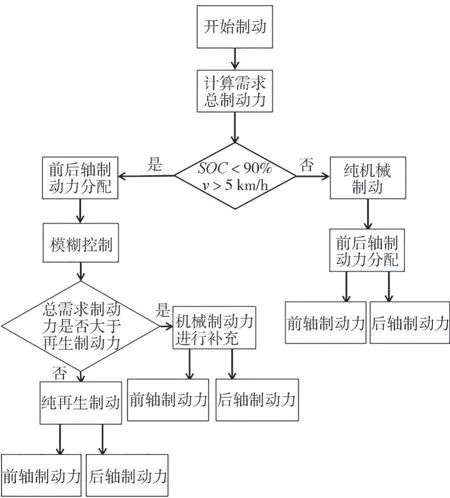
图6 控制流程图

3 建模仿真

为验证优化控制策略的可行性和回收效果，利用Simulink 和AVL Cruise 搭建联合仿真平台。利用Simulink 搭建EMB 数学模型和控制策略模型仿真，利用Cruise 搭建整车模型、电机模型、电池模型等，搭建好的整车模型如图7 所示，搭建好的控制策略模型如图8 所示。通过将Simlink 模型编译成DLL文件接入Cruise 软件中，实现联合仿真。整车模型参数如表2所示。

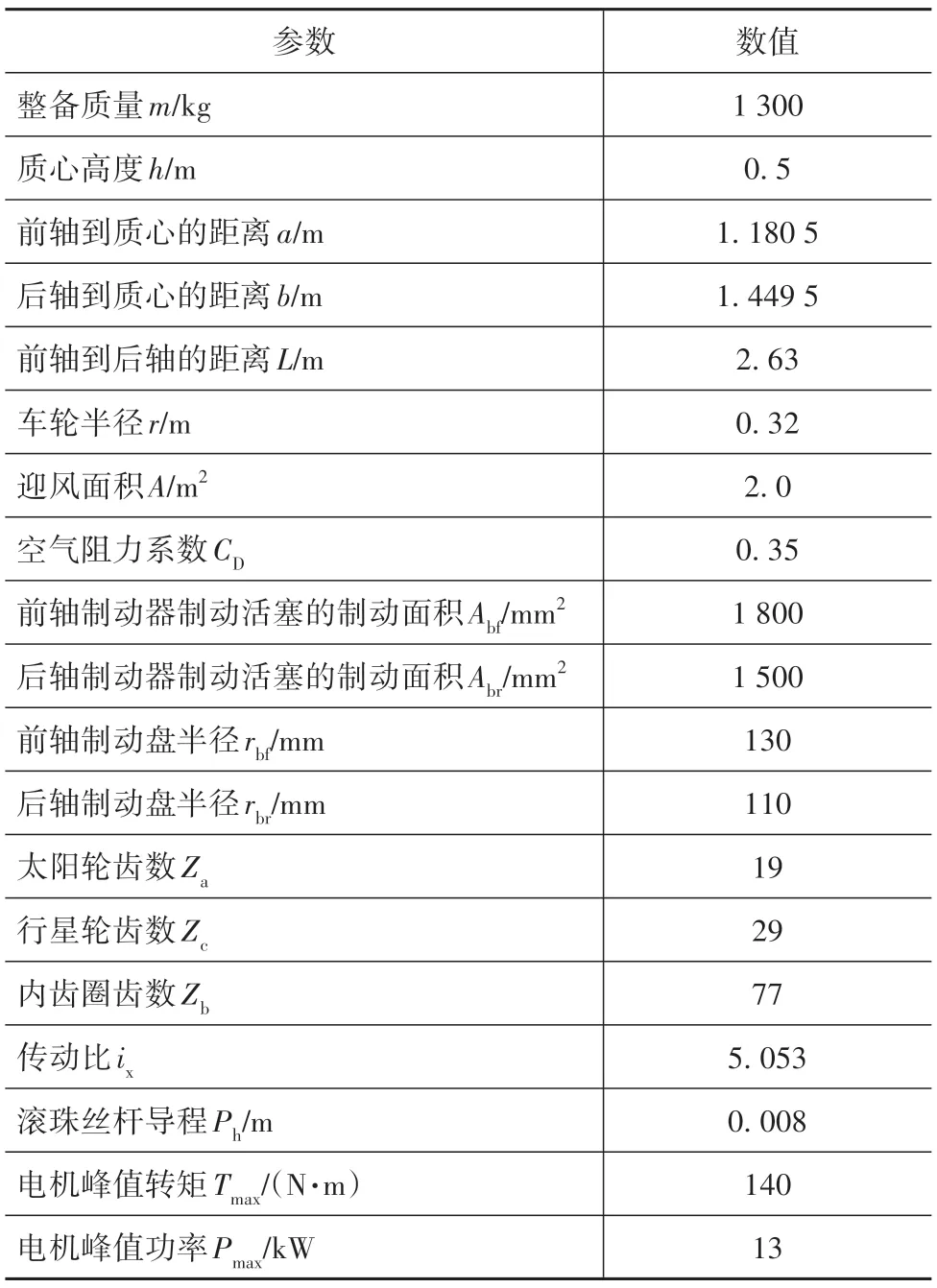
表2 整车模型参数

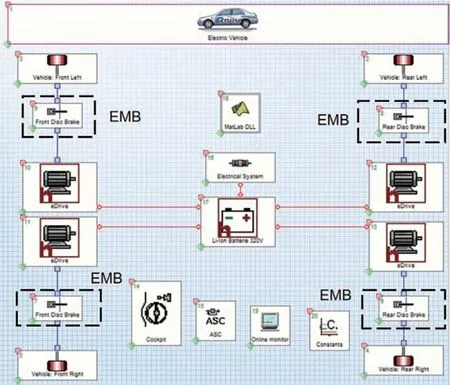
图7 整车模型图

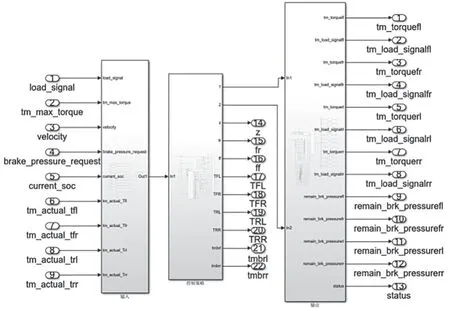
图8 控制策略模型图

4 仿真结果分析

本文中的纯电动汽车采用4 个轮毂电机。在AVL Cruise 中设置仿真工况，分别在典型的NEDC工况和中国城市工况CLTC-P 下进行仿真验证，且利用传统的固定比例回收控制策略进行对比。

4.1 NEDC工况仿真结果分析

NEDC（new European driving cycle）是欧洲的续航测试工况标准，包含4 个市区循环和1 个郊区循环。用本文制定的优化模糊控制策略与优化前的模糊控制策略和经典的固定比例控制策略进行对比，比较制动回收能量和电池SOC值的变化。

图9 为NEDC 速度图，图10 为优化前后再生制动占比系数图，图11 为NEDC 工况下电机和机械制动的转矩图。图中的机械转矩数值较大是因为此时车速低于2.4.3 节中的限定值，汽车逐渐退出再生制动，变为纯机械制动。图12 为整个NEDC 工况下仿真的SOC 变化图，图13 为整个NEDC 工况下回制动收到能量。仿真结果数据如表3 所示。由图12、图13 和表3 可以看出，在NEDC 工况下，通过PSO 算法优化后模糊控制策略再生的制动回收能量最多，比固定比例控制策略多了52.69%，比优化前的模糊控制策略多了2.5%。

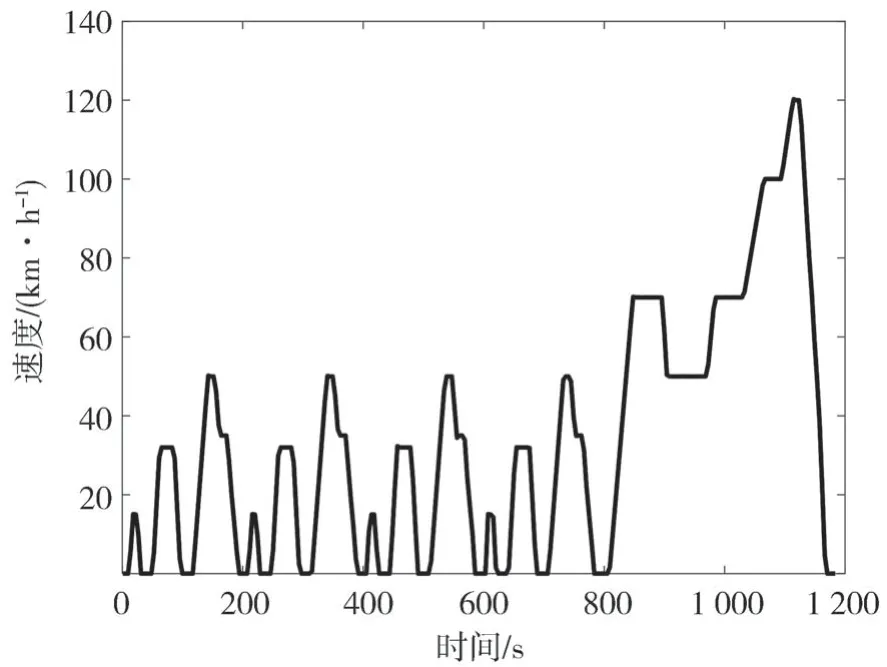
图9 NEDC速度图

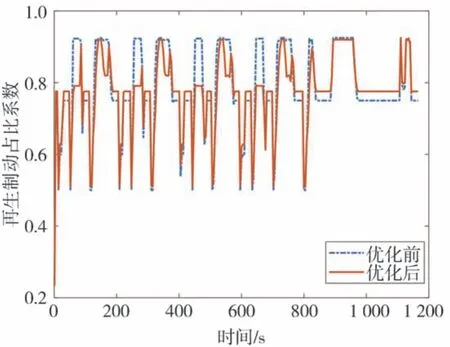
图10 再生制动占比系数图

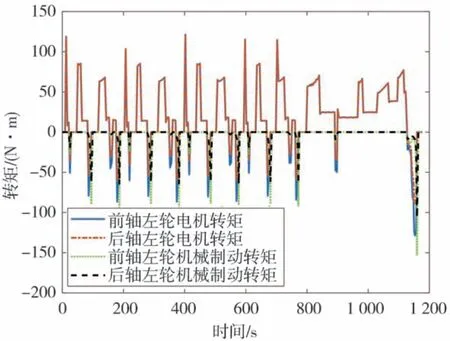
图11 NEDC工况转矩图

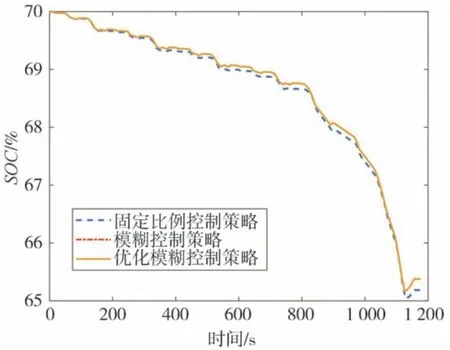
图12 NEDC仿真工况下SOC变化

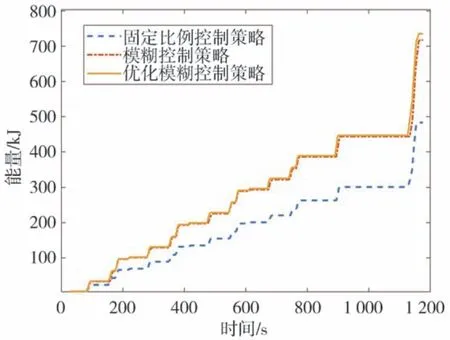
图13 NEDC仿真工况下回收能量

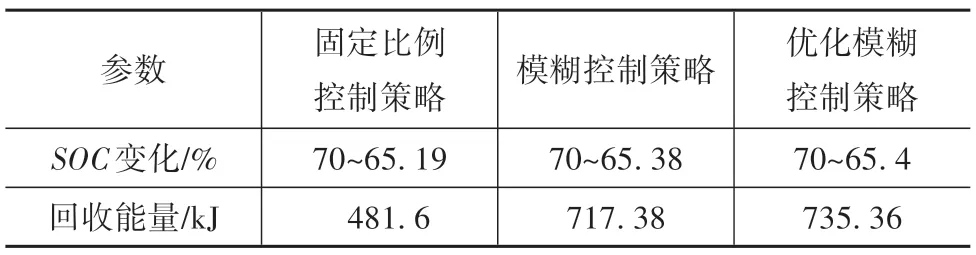
表3 NEDC工况仿真结果

4.2 CLTC-P工况仿真结果分析

CLTC-P（China light-duty vehicle test cyclepassenger）是基于41 座城市、5 000 多辆车，累积5 000 多万km、20 亿条低频交通动态大数据定义的标准工况。CLTC 更真实反映了具有中国特色、高度契合中国交通实际情况的工况，包括更为宽泛的驾驶工况、更为合理的平均车速和停车模式比例以及更为丰富的动态加减速工况。

图14 为CLTC-P 速度图，图15 为优化前后再生制动占比系数图，图16 为CLTC-P 工况下电机和机械制动的转矩图。图中的机械转矩数值较大是因为此时车速低于2.4.3 节中的限定值，汽车逐渐退出再生制动，变为纯机械制动。图17 为整个CLTC-P工况下仿真的SOC 变化图，图18 为整个CLTC-P 工况下制动回收能量，仿真结果数据如表4 所示。由图17、图18 和表4 可以看出，在CLTC-P 工况下，通过PSO算法优化后模糊控制策略的再生制动回收能量最多，比固定比例控制策略多了47.34%，比优化前的模糊控制策略多了1.56%，从而验证了本文控制策略的有效性。

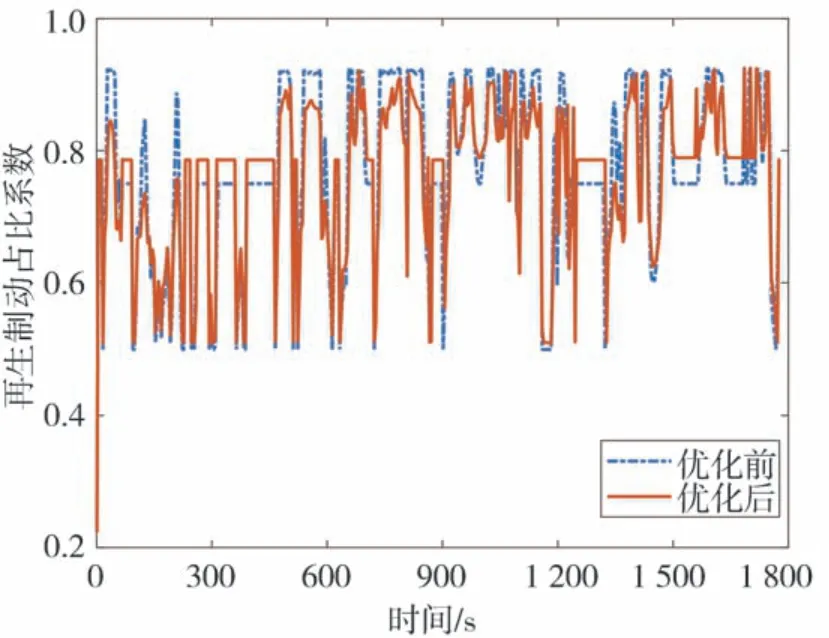
图15 再生制动占比系数图

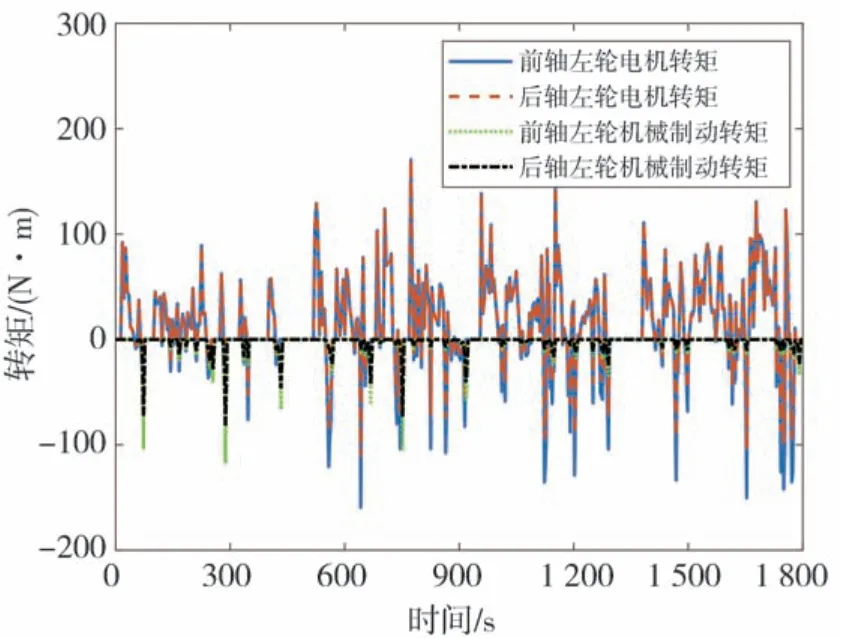
图16 CLTC-P工况转矩图

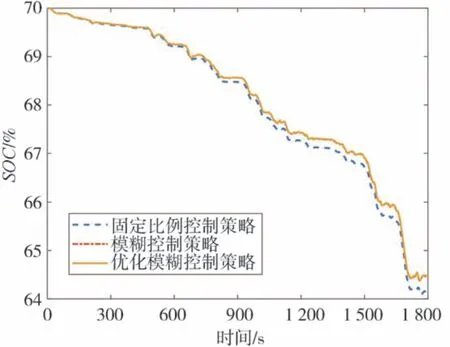
图17 CLTC-P仿真工况下SOC变化

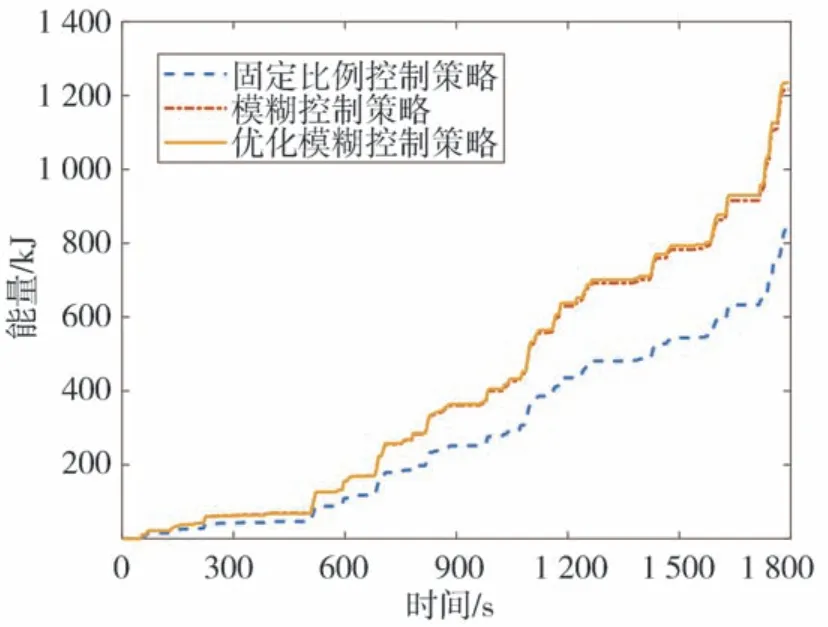
图18 CLTC-P仿真工况下能量回收

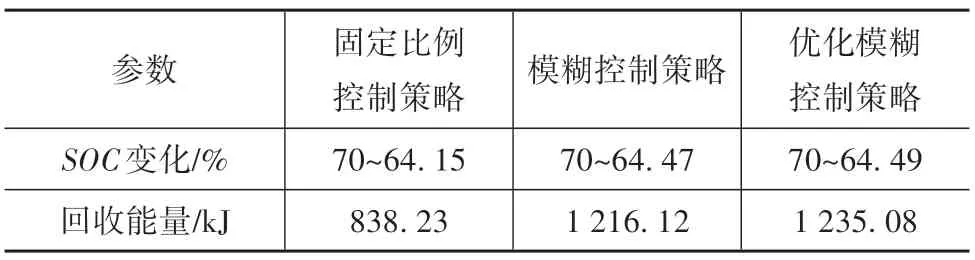
表4 CLTC-P工况仿真结果

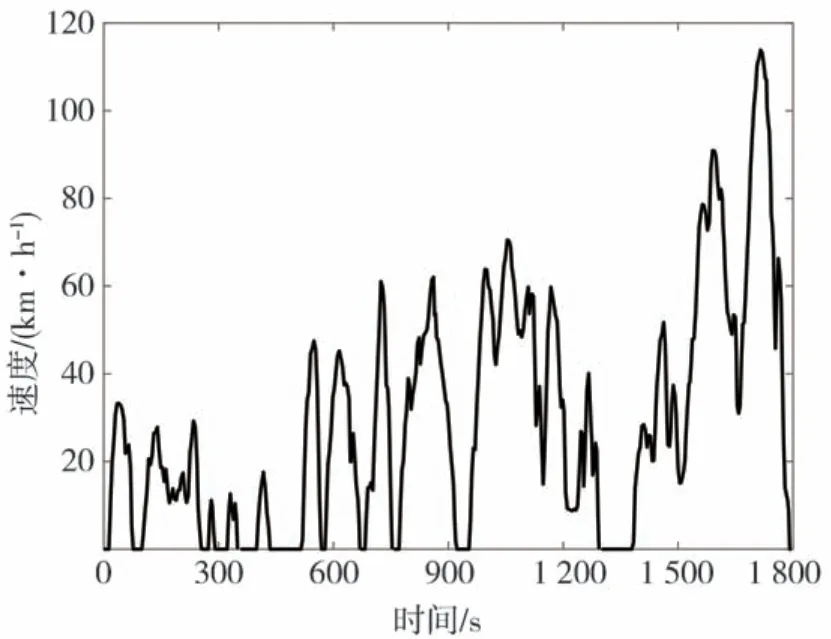
图14 CLTC-P速度图

5 结论

（1）采用响应迅速、反应灵敏的电子机械制动系统代替传统的液压制动系统，使制动更加高效，更有利于配合制动控制策略。

（2）基于电子机械制动系统，考虑ECE 法规、电池SOC 值和车速等约束条件，同时采用了模糊控制器，并利用粒子群算法进行优化。再用Simulink 和AVL Cruise 软件进行联合仿真，在NEDC 和CLTC-P两种典型工况下进行对比。结果表明，该纯电动汽车在本文的控制策略下再生制动回收能量最多。