基于多体经典轨迹蒙特卡罗方法的H+,Li3+,Be4+,O7+与He 原子电荷交换过程*

李国壮 张晟 焦志宏 李新霞

1)(南华大学核科学技术学院,衡阳 421001)

2)(中国科学院近代物理研究所,兰州 730000)

3)(西北师范大学物理与电子工程学院,兰州 730030)

4)(先进能源科学与技术广东省实验室,惠州 516003)

经典轨迹蒙特卡罗(CTMC)方法是研究离子-原子碰撞系统电荷交换过程的常用方法,广泛应用于天体物理以及实验室等离子体环境下重粒子碰撞过程的研究.本文利用四体碰撞模型(4-CTMC)研究了包括两个束缚电子的四体碰撞过程,通过数值求解四体碰撞系统的哈密顿运动方程,计算了高电荷态入射离子(Li3+,Be4+和O7+)同氦原子在大能量范围的单、双电子电离和俘获截面.H++He 碰撞截面的计算中,在50—200 keV/amu的入射能区,4-CTMC 的结果几乎重复了实验结果.在高电荷态入射情形下,4-CTMC 计算的单电子电离和俘获截面值相较于三体碰撞模型(3-CTMC)在100—500 keV/amu 的入射能区内与实验符合更好.尽管4-CTMC 和3-CTMC 忽略了电子关联,均高估了双电子电离和俘获截面(与实验值相比),但4-CTMC 的结果更接近实验.

1 引言

中高能区域(碰撞能:几十keV/amu—百keV/amu)重粒子碰撞的各种反应通道截面对于天体物理[1,2]、受控热核聚变[3,4]、高能量密度物理实验[5,6]以及重离子治疗[7-9]都有十分重要的意义.重粒子碰撞的常用理论模型主要包括平面波玻恩近似(plane-wave Born approximation,PWBA)[10,11]、连续扭曲波 (continuum distorted wave,CDW)近似[12,13]、原子轨道紧耦合(atomic-orbital close-coupling,AOCC)方法[14]、分子轨道紧耦合(molecular-orbital close-coupling,MOCC)方法[15,16]、含时密度泛函方法(time-dependent density functional theory,TDDFT)[17,18]和经典轨迹蒙特卡罗(classical trajectory Monte Carlo,CTMC)方法[19]等.PWBA 和CDW 方法基于确定反应通道的电子初末态波函数计算该通道的截面,因此不能同时给出不同反应通道的截面,这不利于多通道问题的分析.TDDFT 通过完全求解时间依赖的电子密度给出不同反应通道的截面,对计算精度要求很高.半经典的轨道紧耦合方法中,MOCC 方法常用于低能(＜1 keV/amu)离子-分子碰撞问题,AOCC(MOCC)方法的主要优势在于能够清晰地展示各原子态(分子态)之间的跃迁过程.如果不关注各态之间的激发或者退激发过程,利用经典的CTMC方法计算电离和俘获截面具有计算效率高、容易扩展到多电子体系的优势[20,21].当入射离子为高电荷态离子时,三体碰撞模型(3-CTMC)由于使用类氢模型代替双电子体系而容易在低能区域(＜100 keV/amu)高估电离和俘获截面[22,23],特别当电离截面与俘获截面相差5 倍时,计算结果同实验值有较大偏差[24].显然在双电子体系靶的碰撞研究中应该选择四体碰撞模型(4-CTMC).Kirschbaum和Wilets[25]提出含有海森伯不确定原理和泡利不相容原理的Kirschbaum-Wilets CTMC (KWCTMC)模型,可有效地避免双电子体系下的经典自电离.Olson 等[26]在高电荷态离子入射情形下忽略了双电子系统的电子间相互作用,利用Born原子模型研究了电荷交换过程.Frémont[27,28]利用KW-CTMC 模型计算了3.6 MeV 下的Au53+同He 的双微分截面.Bachi 和Otranto[29]研究了50—300 keV 能量区间的H+同He 原子碰撞体系中电子间相互作用对截面的影响.Jorge 等[30]提出switching CTMC (S-CTMC)方法研究了20—200 keV能量区间稳定负氢离子的形成.在S-CTMC 方法中,当靶电子和炮弹的电子束缚于同一原子时,四体模型转换成三体模型计算,而有电子电离或俘获时,则转换回四体模型.当前的研究主要集中在几百keV 的入射能量区间内,还未见有对较大入射能量区间(0.1—5 MeV)碰撞过程的研究.高电荷态的碰撞过程在可控热核聚变或者天体物理研究中具有重要意义:如托克马克装置第一壁材中被化学腐蚀而完全剥离的锂和铍离子[31,32]与等离子体芯部He 原子碰撞的电荷交换过程[4,33],O7+射线同木星大气中He 原子碰撞形成的极光现象[34].

本文基于4-CTMC 模型描述了包含有两个束缚电子的四体碰撞过程,以质子、高电荷态入射离子(Li3+,Be4+和O7+)同He 原子的碰撞体系为例,研究了在较大入射能量区间(0.1—5 MeV)下的作用截面.在我们的程序中,分别对靶原子的两个束缚电子进行逐步判断是否电离,以更新靶核对电子的感应电荷.在计算过程中为了保证计算精度同时节省计算时间,给出了最优的入射离子释放距离和结束判据距离.在低电荷态入射离子的计算案例中(质子入射),低于200 keV/amu 能量区间内,4-CTMC 计算的单电离截面更接近实验值,原因在于4-CTMC 可以更新靶核感应电荷,因此计算结果也更接近实验值.在高电荷态入射离子的计算案例中(Li3+和Be4+入射),在较大能量区间(100—800 keV/amu)内4-CTMC 计算的单电子电离和俘获截面同实验值符合很好.在双电子电离和俘获截面的计算中,高能区的结果接近实验值.整体上,4-CTMC 比3-CTMC 表现更好,原因在于4-CT MC 模型在避免了经典自电离的同时,对包含有两个束缚电子的四体碰撞系统哈密顿运动方程求解.

2 理论模型

如图1 所示,四体碰撞过程要同时确定入射离子、靶核以及两个束缚电子的位置和动量.

图1 四体碰撞系统示意图Fig.1.Four-body collision system.

位置和动量可通过哈密顿运动方程确定:

式中,(Q1,Q2,Q3)表示入射离子A 的位置坐标;(Q4,Q5,Q6)表示靶核B 的位置坐标;(Q7,Q8,Q9)表示轨道电子C 的位置坐标;(Q10,Q11,Q12)表示轨道电子D 的位置坐标,Pj(j=1,2,···,12)为对应的动量.四体碰撞系统的哈密顿量H表示为

(2)式前4 项为入射离子、靶核和两个束缚电子的动能项,后5 项分别为入射离子与靶核、入射离子与电子以及靶核与电子的相互作用项.在碰撞过程中忽略了电子-电子的相互作用,在初始状态中通过中心场近似的屏蔽因子引入[21,26].PA,PB,PC和PD分别表示在实验室坐标系下入射离子、靶核以及两个束缚电子的动量,RAB,RAC,RAD,RBC和RBD表示入射离子、靶核同两个束缚电子之间的距离.

在计算中首先要确定束缚电子的初始状态,在经典框架下描述束缚电子的初始空间分布和动量分布可以采用Reinhold 和Falcón[21]提出的微正则系综的方法:

式中,(x,y,z)表示束缚电子的空间位置;(px,py,pz)表示束缚电子的动量,V(r)和E分别表示相互作用项和电离能.电子初始空间分布和动量分布由6 个随机值r,vr,vp,ω,φr和φp确定,其中r由定积分关系式(4)抽样得到.

碰撞结束时的位置和动量由两处结束判据确定,第一处设置在发生碰撞后略大于释放距离的位置,通常为(10Z+5)a0,Z为入射离子电荷量,a0为玻尔半径,当轨道电子被俘获或者激发,该轨迹停止计算,若发生电离,则在1000Za0处进行第二次结束判据,判断被电离的电子是否再次被入射离子或者靶核俘获.束缚电子终态的判断由相对能量确定,EBC和EBD分别表示电子C 和D 相对于靶核的能量,EAC和EAD分别表示电子C 和D 相对于入射离子的能量,具体判断方法如表1 所列.

表1 4-CTMC 程序中反应类型判据方法Table 1.Criteria followed for the determination of reactions in 4-CTMC method.

当入射离子是高电荷态的离子,碰撞参数较低,且入射离子能量较低时,反应截面相对较高,这时要保留量子干涉效应,而入射离子为高电荷态时,这一特性会显著增加[24],反应概率需要指数近似方法修正:

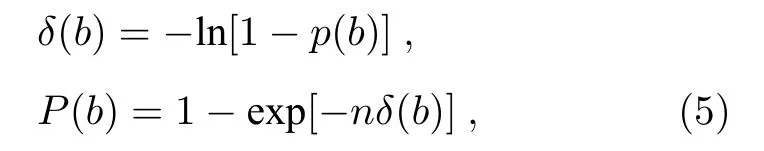
式中,p(b)表示统计得到的反应概率,是关于碰撞参数的函数;P(b)是指数近似后的反应概率;n为靶子的轨道电子数,例如当靶子为氦原子,则n为2.这时,总反应截面σ通过对与碰撞参数b相对应的反应概率P(b)积分得到:

为了保证计算精度同时考虑到计算成本,程序计算的轨迹总数应保证不确定度小于15%[20]:

式中,QR是某一反应的反应截面;N和NR分别表示总计算轨迹数和某一反应对应的事例数,这里5000 条计算轨迹可满足计算精度要求.

3 计算结果及分析

3.1 H+同He 原子的电荷交换过程计算结果

首先展示了低电荷态入射离子(质子)的碰撞案例,分别用3-CTMC 和4-CTMC 方法计算了质子同氦原子的单电子电离和俘获截面,实验数据来自于文献[35].计算过程中,入射离子释放距离RA设置为10a0,时间步长dh设置为1.0×10—5,结束判据距离设置为1000a0.图2(a)显示了两种模型下的单电子电离截面计算结果,同Shah 等[35]的实验结果以及Reinhold 等[21]的计算结果进行了比较,发现在50—200 keV 的入射粒子能量区间,4-CTMC 程序的计算结果相较于3-CTMC 程序和Reinhold 等的计算结果更接近实验结果.在200—1000 keV 的能量区间,两种计算模型同Reinhold 等的计算结果差别不大,但均略小于实验结果,这里考虑的原因可能是高入射能量对应的电离截面较小,需要更多的计算样本数.图2(b)显示了两种模型下的单电子俘获截面计算结果和实验结果,在80—150 keV 的入射粒子能量区间,两种计算模型的单电子俘获截面的计算结果同实验符合较好,在150—250 keV 能量区间,3-CTMC程序的结果略低于实验值,原因可能由于三体碰撞系统计算作用截面时,若俘获截面同电离截面相差一个量级,会存在一定误差[24].

图2 (a)H++He 单电子电离截面;(b)H++He 单电子俘获截面Fig.2.The H++He total cross section for (a)single ionization and (b)electron capture as a function of the projectile energy.

另外,质子算例的计算结果显示,当相应的反应截面低于5×10—17cm2时,计算值相较于实验值偏低,考虑的原因是在某一能量区间,相应反应类型对应的事例数较少,处于竞争关系下的其他反应类型对应事例数较多,因此出现了统计偏差,可通过增加计算轨迹数提高计算准确度,但相应会增加计算时间,如何提高计算速度同时保证准确度,这将是我们今后改进4-CTMC 程序的主要方向.

图3 展示了分别利用3-CTMC 和4-CTMC程序计算得到的质子同氦原子的双电离截面,实验数据来自文献[35],红色虚线是Reinhold 等[21]的计算结果.结果显示,对于双电子电离过程,由于4-CTMC 对电离过程进行了类似分步电离的处理,在计算中每步计算结束对束缚电子判断是否电离,进而更新靶核对另一电子的感应电荷,因此4-CT MC 计算结果更接近实验值.产生偏差的原因在于将双电子电离过程分离处理,低估了靶核对于轨道电子的束缚,此外未考虑电子间相互作用,从而忽略了如电子发射这类电子间相互作用导致的机制.

图3 H++He 双电子电离截面Fig.3.The H++He total cross section for double ionization.

3.2 高电荷态入射离子同He 原子的电荷交换过程计算结果

接下来展示了高电荷态入射离子的碰撞案例,利用3-CTMC 和4-CTMC 程序计算了全剥离锂离子与氦原子的单电子电离和俘获截面,如图4(a)和图4(b)所示.计算过程中,入射离子释放距离RA设置为30a0,时间步长dh设置为1.0×10—5,结束判据距离设置为3000a0.值得一提的是,全剥离的锂离子相较于质子有较高的电荷态,为了避免入射离子释放距离过小而扰动束缚电子的初始状态,入射离子的释放距离选取为10Za0[20],Z为入射离子电荷量.也有文献提出为了忽略入射离子的初始扰动,释放距离至少为4 倍的最大碰撞参数[8].以全剥离锂离子与氦原子的碰撞体系为例,最大碰撞参数为5a0,则相应的释放距离至少为20a0.这里采取第一种方式选取释放距离为10Za0(即30a0)来避免入射离子扰动.此外在碰撞系统的初态确定阶段,入射离子释放距离不宜过大,首先会增加计算成本,其次过大的释放距离,将延长整个碰撞过程的持续时间,从而放大了束缚电子在轨道上受到的扰动[19].图4 中实验值来自Pivovar 等[36]以及Santanna 等[37]的测量结果(较高能量部分(＞2 MeV)来自文献[37]),3-CTMC 方法在1.5—6.0 MeV 的能量区间略高于实验值,4-CTMC 计算结果同实验符合更好.4-CTMC 方法的计算结果相较于3-CTMC 方法更接近实验结果.

图4 (a)Li3++He 单电子电离截面;(b)Li3++He 单电子俘获截面Fig.4.The Li3++He total cross section for (a)single ionization and (b)electron capture as a function of the projectile energy.

图5(a)和图5(b)分别显示了全剥离锂离子同氦原子的双电离与双俘获截面,实验数据来自文献[37].计算结果显示,类似质子的案例,对于双电子过程,同实验值仍有较大的偏差,但4-CTMC 方法相较于3-CTMC 方法更接近实验结果.

图5 (a)Li3++He 双电子电离截面;(b)Li3++He 双电子俘获截面Fig.5.The Li3++He total cross section for (a)double ionization and (b)electron capture as a function of the projectile energy.

进一步计算了全剥离铍离子与氦原子的单电子电离和俘获截面,计算过程中,入射离子释放距离RA设置为40a0,时间步长dh设置为1.0×10—5,结束判据距离设置为4000a0.图6(a)显示了3-CT MC 和4-CTMC 方法的单电子电离截面结果,目前缺少全剥离铍离子的实验结果,电离以及俘获截面的对比结果来自Olson[24]的理论计算值,3-CT MC 方法的计算结果在2.0—4.5 MeV 的能量区间略高于4-CTMC 方法.图6(b)显示了相应的单电子俘获截面计算结果,同样地,4-CTMC 方法的计算结果更接近Olson[24]的理论计算值.

图6 (a)Be4++He 单电子电离截面;(b)Be4++He 单电子俘获截面Fig.6.The Be4++He total cross section for (a)single ionization and (b)electron capture as a function of the projectile energy.

图7 显示了分别利用3-CTMC 和4-CTMC程序计算得到的全剥离铍离子同氦原子的双电离与双俘获截面.计算结果显示,对于双电子过程,在较低能量区间,计算结果差别不大,在2.0—4.5 MeV 能量区间,4-CTMC 方法相较于3-CTMC方法计算值更低.

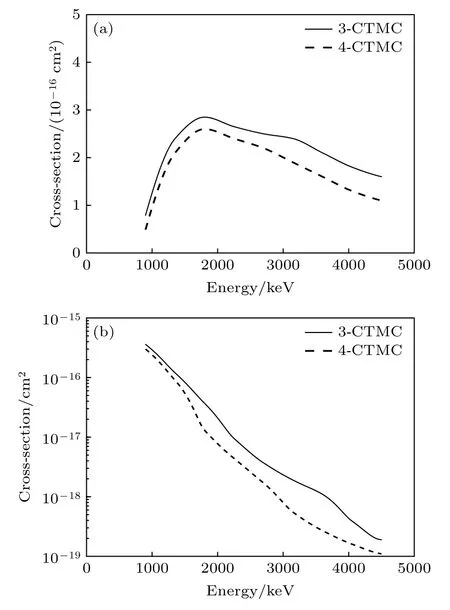
图7 (a)Be4++He 双电子电离截面;(b)Be4++He 双电子俘获截面Fig.7.The Be4++He total cross section for (a)double ionization and (b)electron capture as a function of the projectile energy.

最后,图8 显示了利用4-CTMC 所计算的氧离子(O7+)同氦原子碰撞体系的单、双电离和俘获截面,图中SI,SC,DI 和DC 分别表示单电离、单俘获、双电离和双俘获.入射离子能量区间为0.8—7.2 MeV,在入射离子能量接近2 MeV 时,单电离截面超过单俘获和双俘获截面,在入射离子能量接近2.5 MeV 时,双电离截面超过单、双俘获截面,并且随着入射离子能量逐渐增加,电荷交换过程将以电离过程为主,电子俘获过程尤其双电子俘获所占份额将显著下降.该碰撞体系下的预测结果有待实验进一步验证.

图8 O7++He 碰撞体系的4-CTMC 计算结果Fig.8.The O7++He total cross section calculated by 4-CTMC.

4 结论

本文基于3-CTMC 方法,在碰撞体系中考虑两个束缚电子,扩展得到了4-CTMC 程序,并分别用这两种计算模型,计算了质子、高电荷态入射离子(Li3+,Be4+和O7+)同氦原子的电离和俘获截面,当质子为入射离子时,在低于200 keV 的能量区间,4-CTMC 单电离计算结果更接近实验值,而对于高电荷态的入射离子(Li3+和Be4+),在100—500 keV/amu 区间同实验结果符合更好,原因在于4-CTMC 模型在避免了经典自电离的同时,考虑包含两个束缚电子的四体碰撞系统哈密顿量,可以更精确地描述双电子体系.对于上述的任何一个算例,4-CTMC 方法的计算时长均大于3-CTMC方法,在时间步长、结束判据距离等计算参数一致的情况下,4-CTMC 方法的计算时长要比3-CTMC方法超出约30%.需要指出的是,4-CTMC 和3-CT MC 会对四体碰撞过程的双电子电离、俘获截面整体高估,可能的原因是忽略了碰撞过程中电子间相互作用.下一步的工作中我们将考虑四体碰撞过程中的电子-电子间关联效应[38].